Содержание
- 2. Работа при движении по всей траектории из точки 1 в точку 2 равна; Такие поля называются
- 3. называется циркуляцией вектора напряженности, и представляет собой работу при перемещении единичного положительного заряда. т.е. линейный интеграл
- 4. Потенциальная энергия заряда В потенциальном поле тела обладают потенциальной энергией и тела могут совершать работу за
- 5. 10. Потенциал и разность потенциалов электростатического поля заряда Энергетическая характеристика поля, независящая от пробного заряда q0
- 6. Из определения потенциала видно, что это алгебраическая величина:
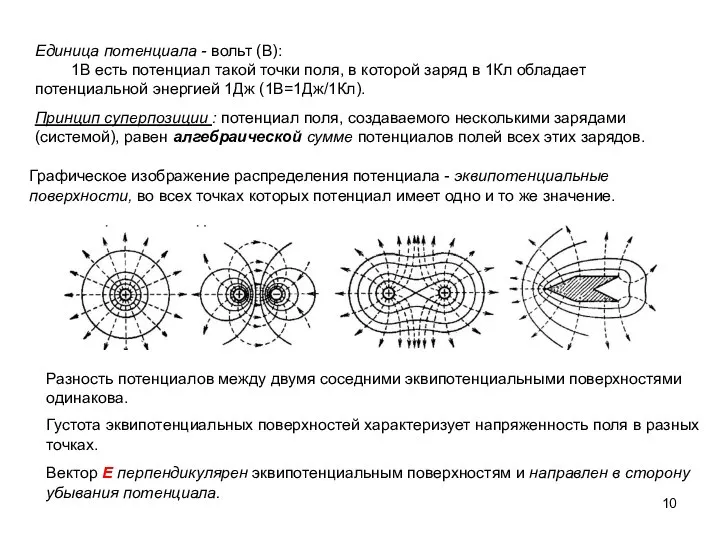
- 7. Связь между напряженностью поля и потенциалом. Поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной: Если
- 8. Зададим две эквипотенциальные поверхности с потенциалами: Расстояние между поверхностями очень мало так, что напряженность не меняется
- 9. 1. Потенциал бесконечно заряженной плоскости между точками, лежащими на расстояниях х1, и x2 от плоскости: 2.
- 10. Единица потенциала - вольт (В): 1В есть потенциал такой точки поля, в которой заряд в 1Кл
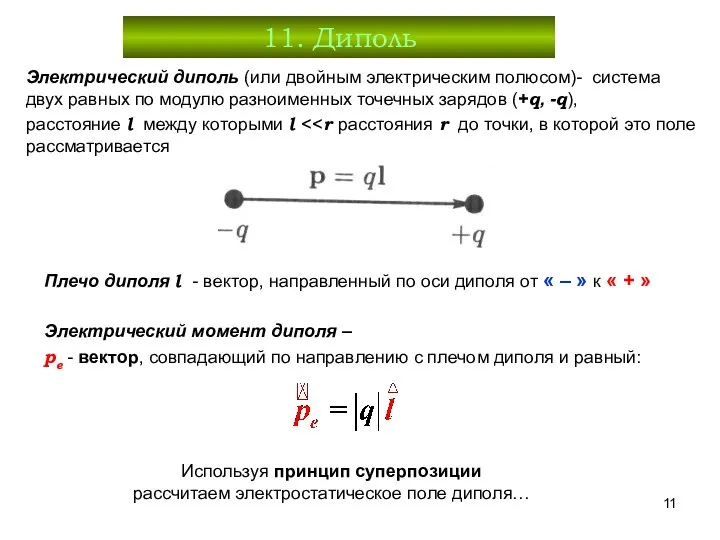
- 11. 11. Диполь Электрический диполь (или двойным электрическим полюсом)- система двух равных по модулю разноименных точечных зарядов
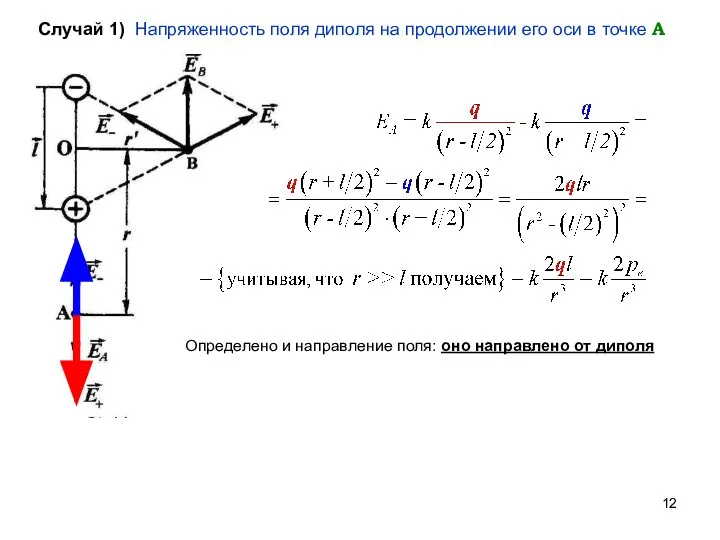
- 12. Случай 1) Напряженность поля диполя на продолжении его оси в точке А Определено и направление поля:
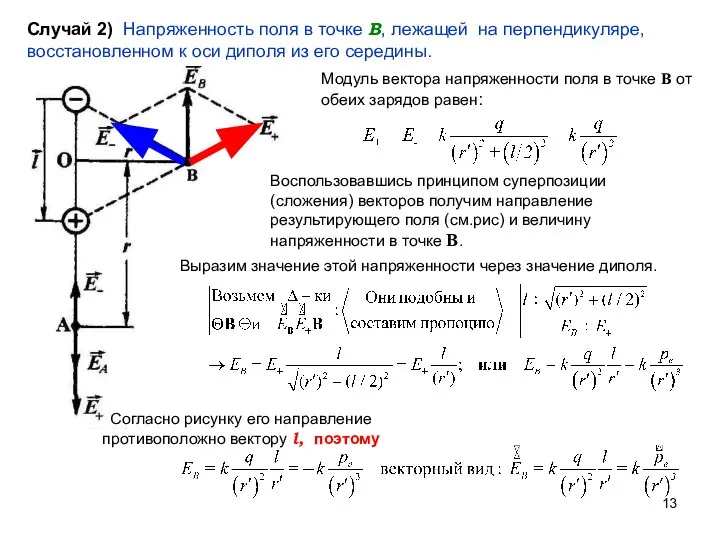
- 13. Случай 2) Напряженность поля в точке В, лежащей на перпендикуляре, восстановленном к оси диполя из его
- 14. Общий случай 3) сводится к двум рассмотренным частным. Постановка задачи: Найти напряженность поля диполя p (ВС)
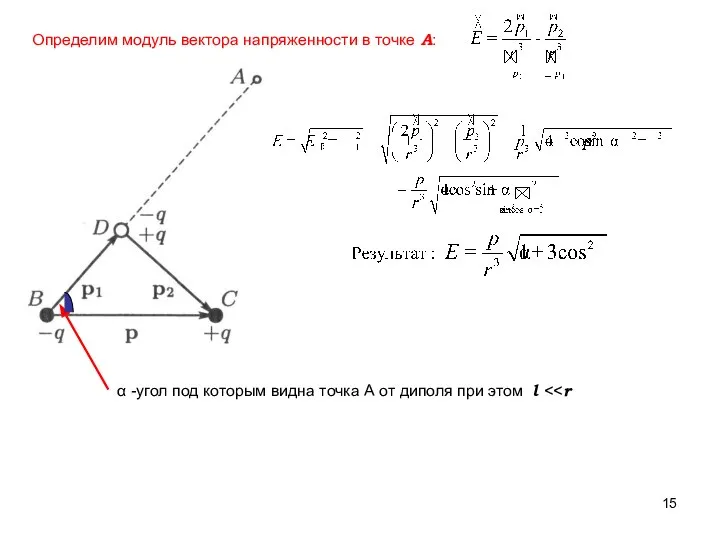
- 15. Определим модуль вектора напряженности в точке А: α -угол под которым видна точка А от диполя
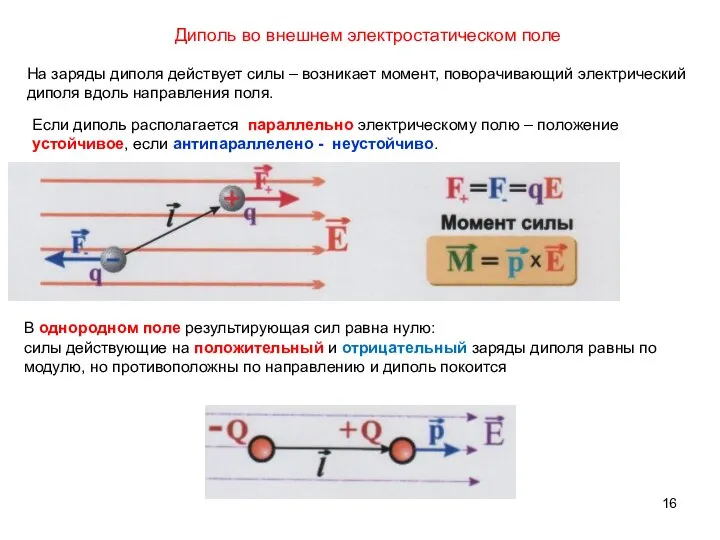
- 16. Диполь во внешнем электростатическом поле В однородном поле результирующая сил равна нулю: силы действующие на положительный
- 18. Скачать презентацию









 Радиоактивные превращения атомных ядер
Радиоактивные превращения атомных ядер Как подготовить велосепед к сезону
Как подготовить велосепед к сезону Оценивание заданий с развёрнутыми ответами ОГЭ по физике
Оценивание заданий с развёрнутыми ответами ОГЭ по физике Элементы теории электромагнетизма Максвелла. Лекция 14
Элементы теории электромагнетизма Максвелла. Лекция 14 Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц В каком мире жили наши предки?
В каком мире жили наши предки? Радиация вокруг нас
Радиация вокруг нас Тайна ключа
Тайна ключа Давление жидкостей и газов. Игра – путешествие
Давление жидкостей и газов. Игра – путешествие Сила пара
Сила пара Строительная механика
Строительная механика Проработка конструкции двигателя ЗМЗ 53. Разработка технологического процесса
Проработка конструкции двигателя ЗМЗ 53. Разработка технологического процесса Применение силы Лоренца
Применение силы Лоренца Кинематика материальной точки и твердого тела
Кинематика материальной точки и твердого тела Техническая диагностика подвижного состава. Магнитный контроль
Техническая диагностика подвижного состава. Магнитный контроль Организация проектно-исследовательской деятельности на уроках физики как путь к формированию ключевых компетенций
Организация проектно-исследовательской деятельности на уроках физики как путь к формированию ключевых компетенций Ремонт_рулевого_управления_разных_видов
Ремонт_рулевого_управления_разных_видов Презентация на тему Механическая энергия. Закон сохранения энергии
Презентация на тему Механическая энергия. Закон сохранения энергии 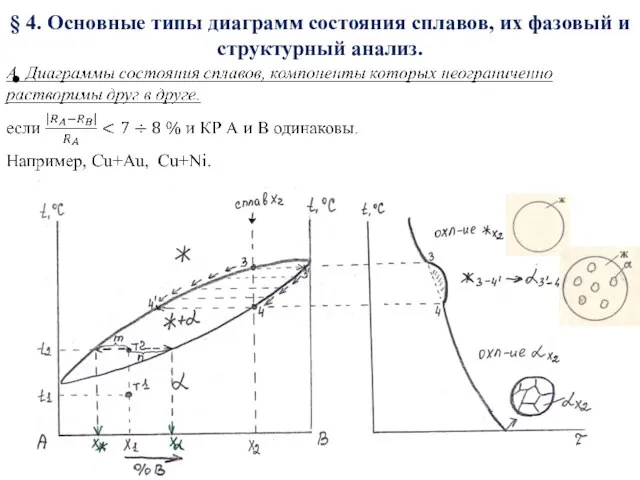 Диаграммы состояния сплавов, их фазовый и структурный анализ
Диаграммы состояния сплавов, их фазовый и структурный анализ Червячные передачи
Червячные передачи Основные положения молекулярно-кинетической теории
Основные положения молекулярно-кинетической теории Уравнение Клапейрона
Уравнение Клапейрона Плотность. Расчет массы и объема тела по его плотности
Плотность. Расчет массы и объема тела по его плотности АТОМНЫЕ ЭЛЕКТРОСТАНЦИИ С РЕАКТОРАМИ НА БЫСТРЫХ НЕЙТРОНАХ
АТОМНЫЕ ЭЛЕКТРОСТАНЦИИ С РЕАКТОРАМИ НА БЫСТРЫХ НЕЙТРОНАХ Основные понятия о точности и взаимозаменяемости
Основные понятия о точности и взаимозаменяемости лекция 4_дифр Фраунгофера на ДР
лекция 4_дифр Фраунгофера на ДР Решение задач. Силы тяжести, упругости
Решение задач. Силы тяжести, упругости Беспроводные системы охраны периметра. Радиолучевая система охраны периметра
Беспроводные системы охраны периметра. Радиолучевая система охраны периметра