способы решения
Система уравнений Максвелла для электромагнитного поля: смысл, способы решения
Полезно знать Подготовка к экзамену Физика для "чайников"
Иван27 Июнь 201717 264
Нет времени писать работу?
Доверь это кандидату наук!
Узнай стоимость
Содержание
Содержание
Первое уравнение Максвелла
Третье уравнение Максвелла
Второе уравнение Максвелла
Четвертое уравнение Максвелла
Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.
Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.
Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.
Тем не менее, и по сей день нет никаких сомнений в правильности уравнений Максвелла, они «работают» не только в привычном нам макромире, но и в области квантовой механики.
Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.
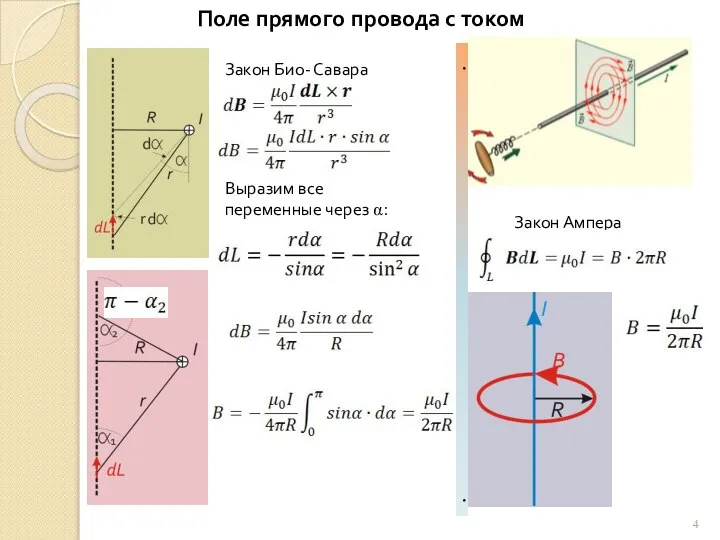
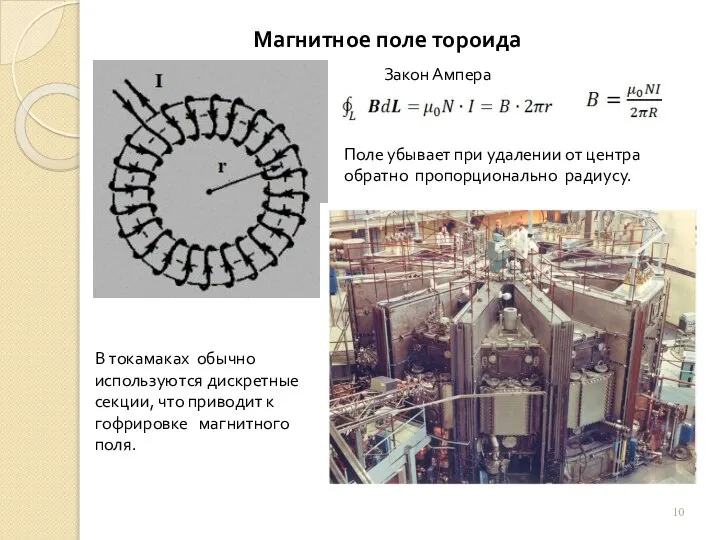
Закон Ампера
Четвертое уравнение Максвелла
В случае магнитостатики можно использовать
в виде .
Воспользовавшись теоремой Стокса, получим:
Циркуляция индукции по контуру равна току внутри контура:
Закон удобно использовать в симметричных случаях, когда В на контуре можно считать постоянным.
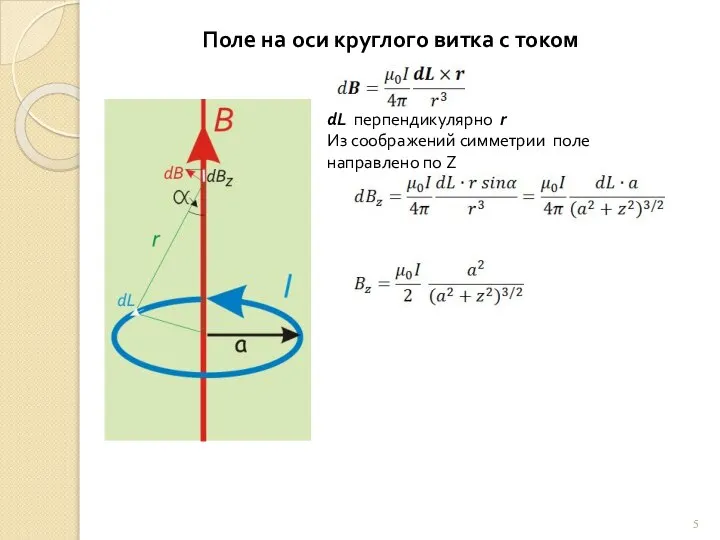
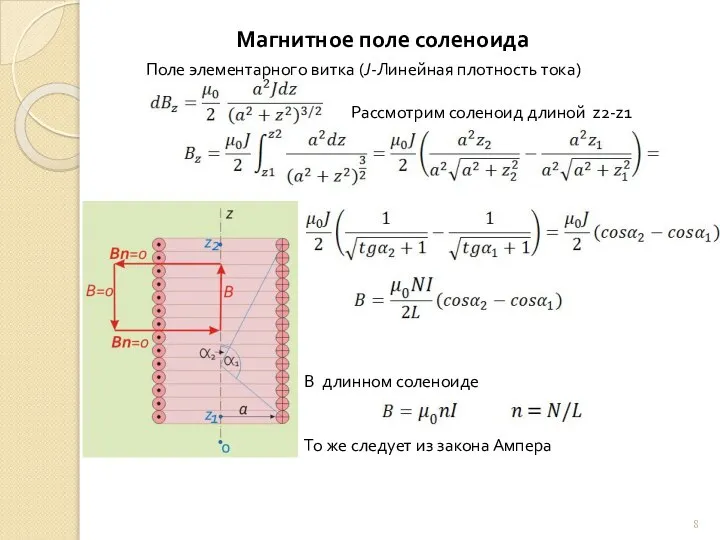
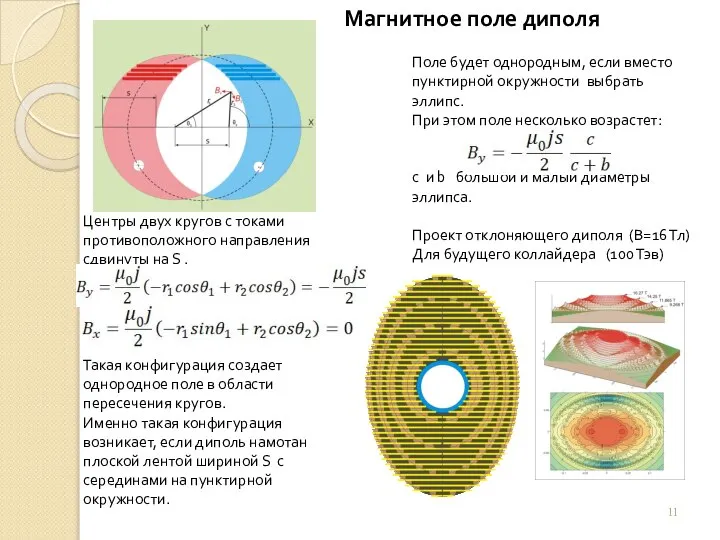
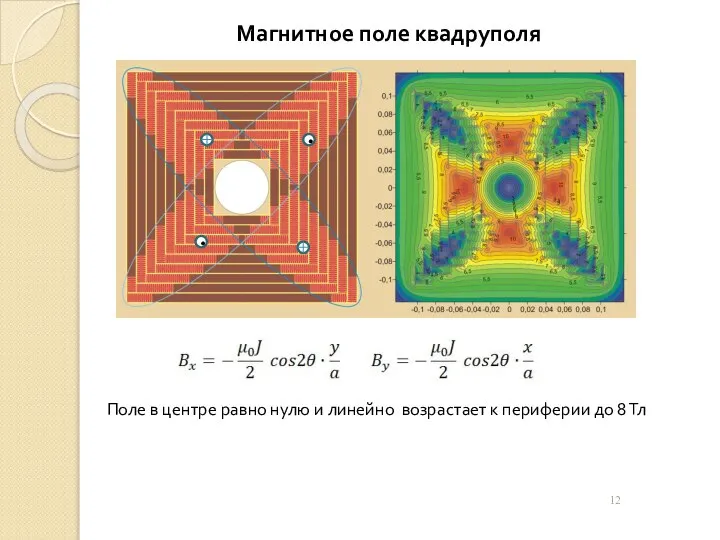
У нас теперь два метода расчета магнитного поля: Закон Био-Савара и Ампера. Рассмотрим параллельно несколько задач. .









 Методы исследования частиц
Методы исследования частиц Приемы выполнения фальцевого и заклепочного швов и соединения деталей
Приемы выполнения фальцевого и заклепочного швов и соединения деталей Ультрафиолетовое и инфракрасное излучения. Рентгеновские лучи. Практическая работа №22
Ультрафиолетовое и инфракрасное излучения. Рентгеновские лучи. Практическая работа №22 Магнитное поле Земли
Магнитное поле Земли Технология подготовки машинно-тракторного агрегата для внесение минеральных удобрений и выполнение работ на нем
Технология подготовки машинно-тракторного агрегата для внесение минеральных удобрений и выполнение работ на нем 13. СВЕТОТЕХНИКА 2020
13. СВЕТОТЕХНИКА 2020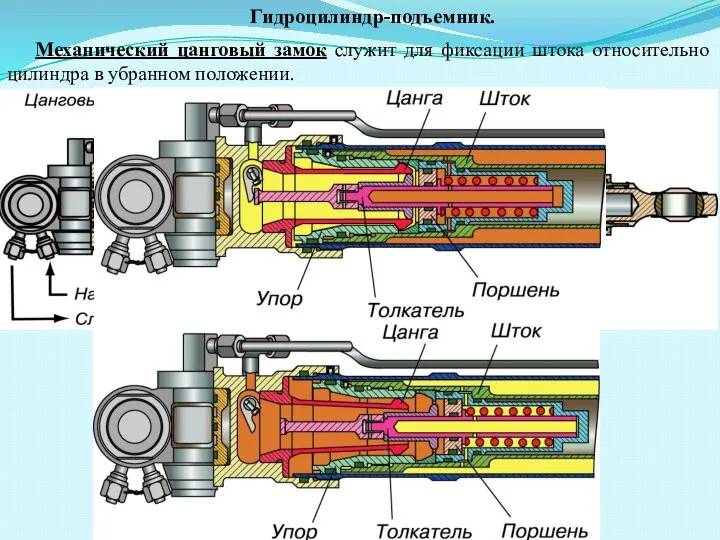 Гидроцилиндр-подъемник
Гидроцилиндр-подъемник Расчет пути и времени движения
Расчет пути и времени движения Презентация на тему Архимедова сила и ее значение в жизни человека
Презентация на тему Архимедова сила и ее значение в жизни человека  Статистическая теория радиотехнических систем. Случайные процессы и величины. (Лекция 2)
Статистическая теория радиотехнических систем. Случайные процессы и величины. (Лекция 2) Явление самоиндукции
Явление самоиндукции Тест по физике. «Импульс. Закон сохранения импульса» 9 класс
Тест по физике. «Импульс. Закон сохранения импульса» 9 класс Постоянно изменяемые фазы газораспределения. Системы CVVT
Постоянно изменяемые фазы газораспределения. Системы CVVT Типология транспорта для уборки улиц и общественнх учреждений
Типология транспорта для уборки улиц и общественнх учреждений Повышение КПД ГТУ путём внедрения регенеративного цикла
Повышение КПД ГТУ путём внедрения регенеративного цикла Термоядерные реакции. (Тема 2.4)
Термоядерные реакции. (Тема 2.4) Тайна воды, которую мы прием
Тайна воды, которую мы прием Идеальный газ. Абсолютная температура. Макро и микропараметры
Идеальный газ. Абсолютная температура. Макро и микропараметры Динамика материальной точки
Динамика материальной точки Подготовка к ЕГЭ. Решение задач
Подготовка к ЕГЭ. Решение задач Презентация на тему Молекулы. Диффузия. Взаимодействие молекул
Презентация на тему Молекулы. Диффузия. Взаимодействие молекул  Диэлектрики. Введение
Диэлектрики. Введение Тормозной путь автомобиля
Тормозной путь автомобиля Физический диктант по теме: Механические колебания
Физический диктант по теме: Механические колебания Фотоэффект. Применение фотоэффекта
Фотоэффект. Применение фотоэффекта Расчет статических нагрузок тела под собственным весом
Расчет статических нагрузок тела под собственным весом Промежуточные фазы. Электронные соединения
Промежуточные фазы. Электронные соединения Safarov_Krasnov
Safarov_Krasnov