Содержание
- 2. Лекция 1. Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля Электрический заряд.
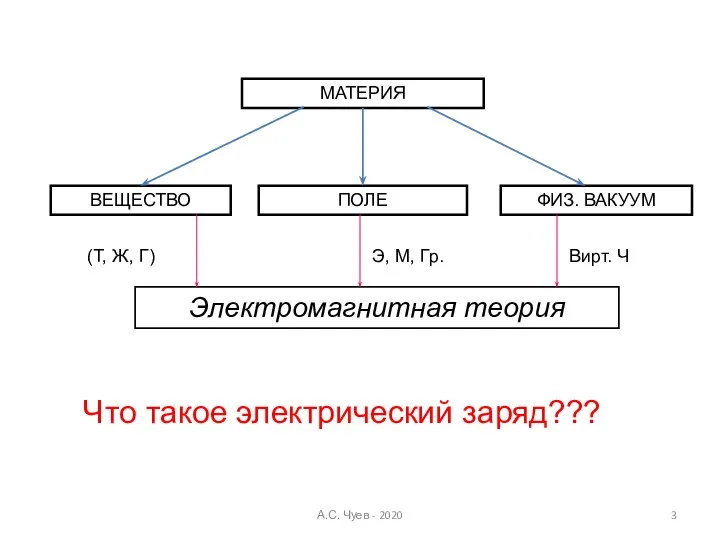
- 3. МАТЕРИЯ ВЕЩЕСТВО ПОЛЕ ФИЗ. ВАКУУМ (Т, Ж, Г) Электромагнитная теория Э, М, Гр. Вирт. Ч Что
- 4. А.С. Чуев - 2020
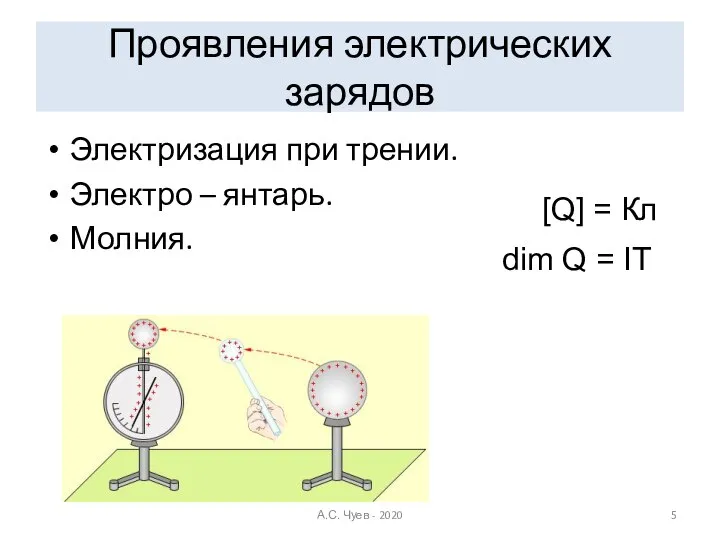
- 5. Проявления электрических зарядов Электризация при трении. Электро – янтарь. Молния. dim Q = IT [Q] =
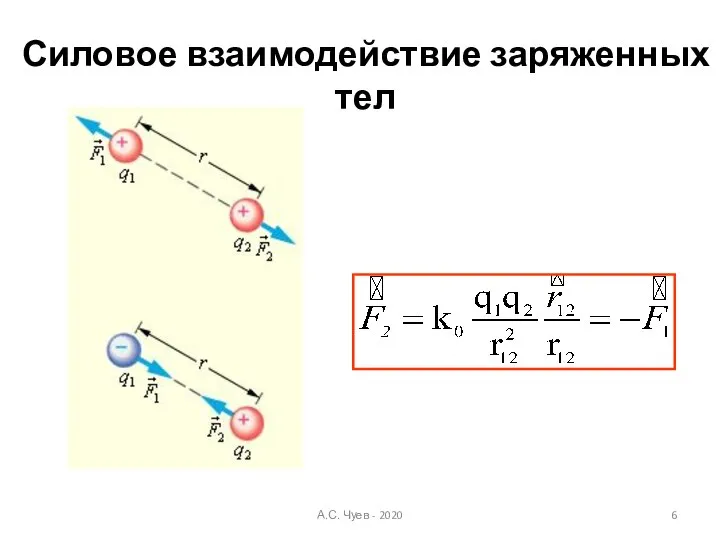
- 6. Силовое взаимодействие заряженных тел А.С. Чуев - 2020
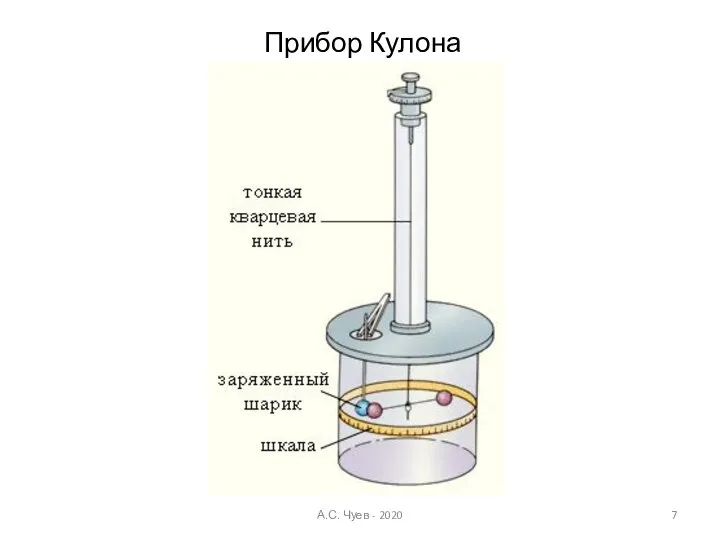
- 7. Прибор Кулона А.С. Чуев - 2020
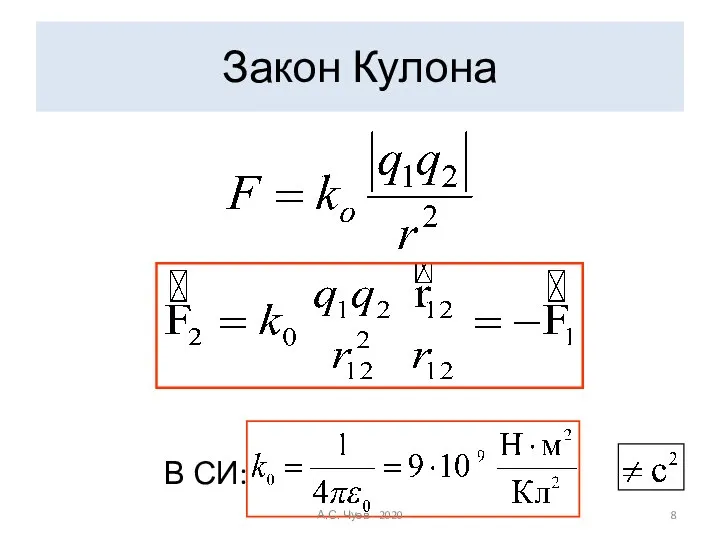
- 8. Закон Кулона В СИ: А.С. Чуев - 2020
- 9. Электрические заряды не существуют сами по себе, а являются внутренними свойствами элементарных частиц – электронов, протонов
- 10. Определения плотностей заряда: – линейная плотность заряда, измеряется в Кл/м; - поверхностная плотность заряда измеряется в
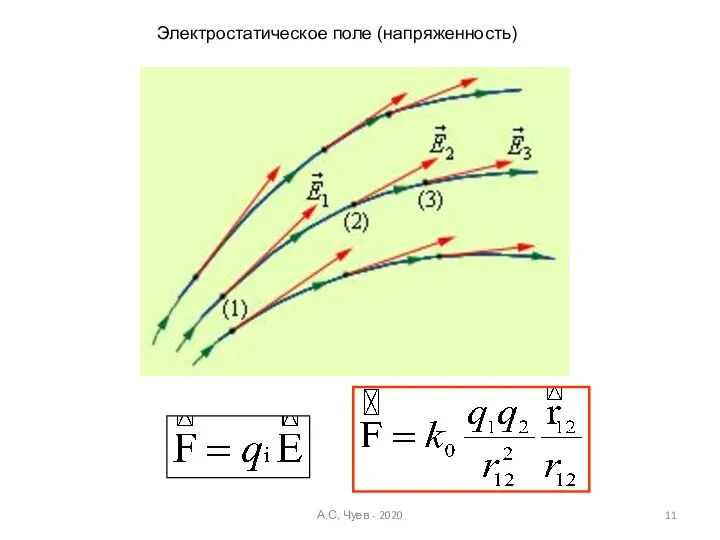
- 11. А.С. Чуев - 2020 Электростатическое поле (напряженность)
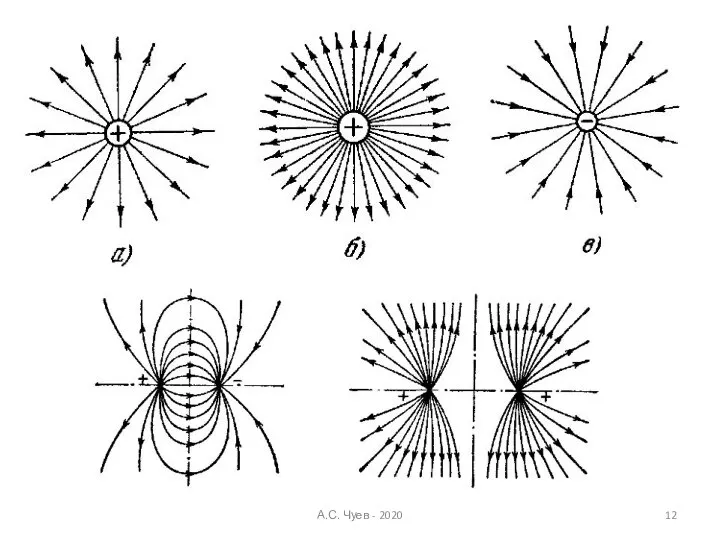
- 12. А.С. Чуев - 2020
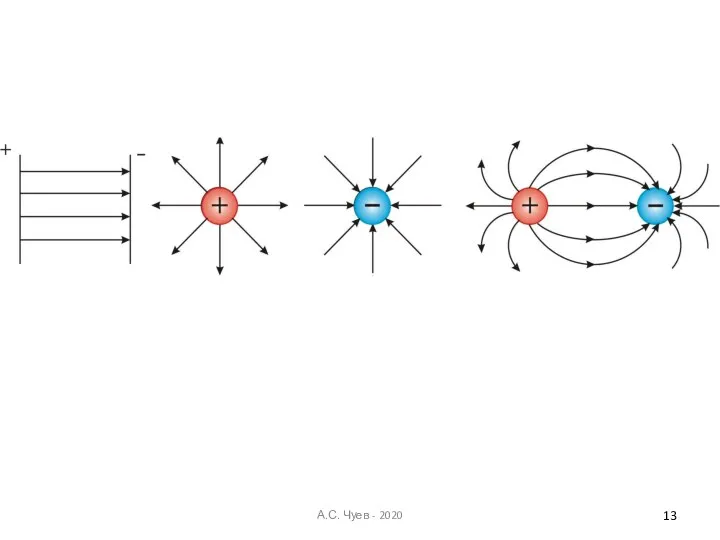
- 13. А.С. Чуев - 2020
- 14. Силовая характеристика электростатического поля - напряженность Определение Е со стороны пробного заряда: это отношение силы к
- 15. В скалярном виде: Иная форма записи : здесь r – расстояние от заряда q до точки,
- 16. Энергетическая характеристика электростатического поля – электрический потенциал (скалярный) Определение потенциала со стороны пробного заряда: это отношение
- 17. А.С. Чуев - 2020
- 18. А.С. Чуев - 2020
- 19. А.С. Чуев - 2020
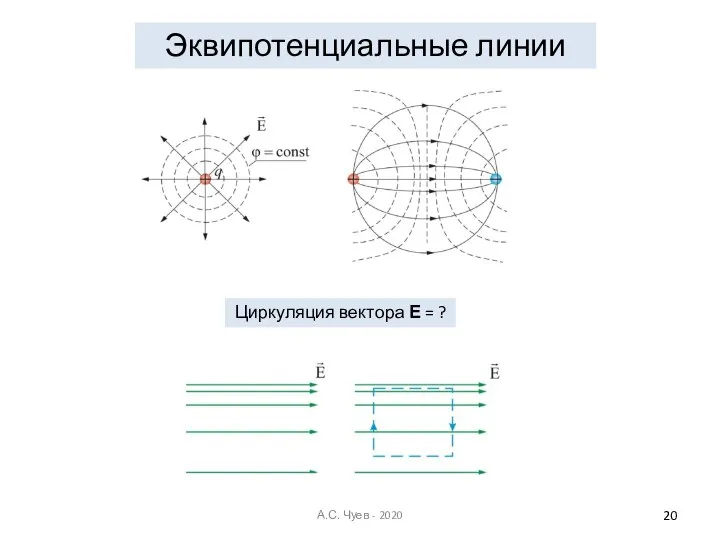
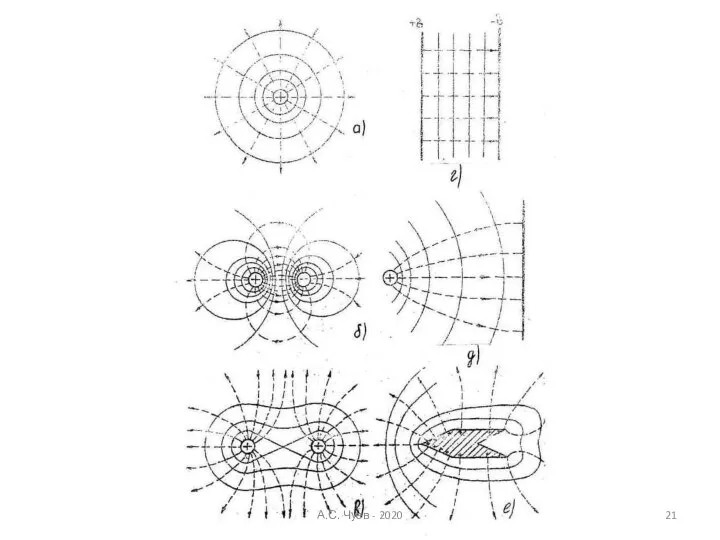
- 20. Эквипотенциальные линии Циркуляция вектора Е = ? А.С. Чуев - 2020
- 21. А.С. Чуев - 2020
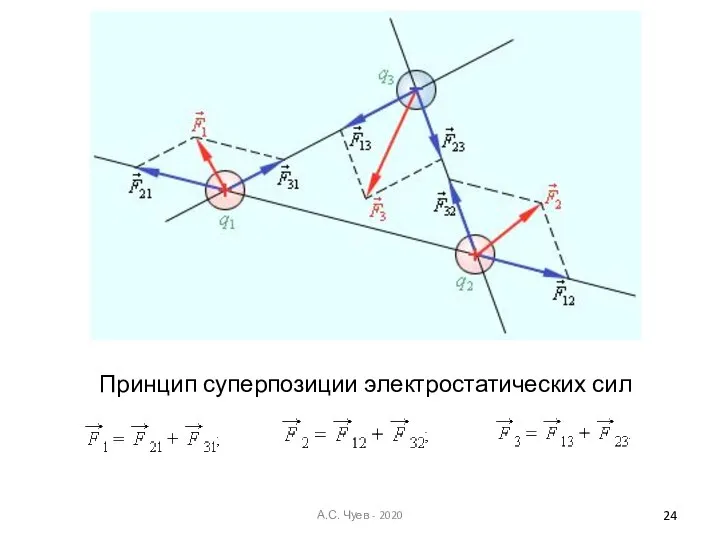
- 22. Сложение действия электростатических сил. Принцип суперпозиции Если поле создается несколькими точечными зарядами, то на пробный заряд
- 23. Напряженность результирующего поля, системы точечных зарядов равна векторной сумме напряженностей полей, созданных в данной точке каждым
- 24. Принцип суперпозиции электростатических сил А.С. Чуев - 2020
- 25. Электрический диполь Электрический дипольный момент А.С. Чуев - 2020
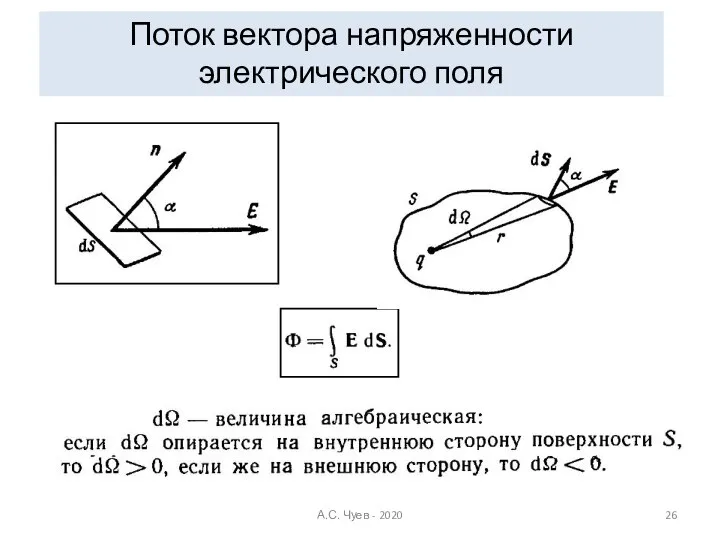
- 26. Поток вектора напряженности электрического поля А.С. Чуев - 2020
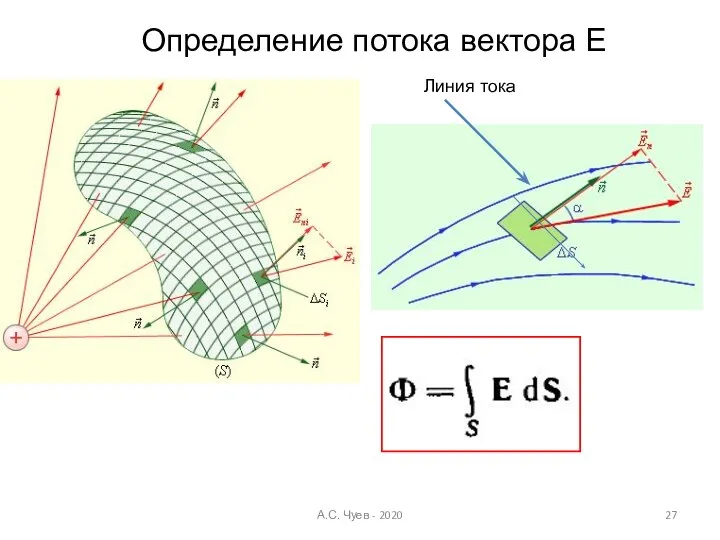
- 27. Определение потока вектора Е А.С. Чуев - 2020 Линия тока
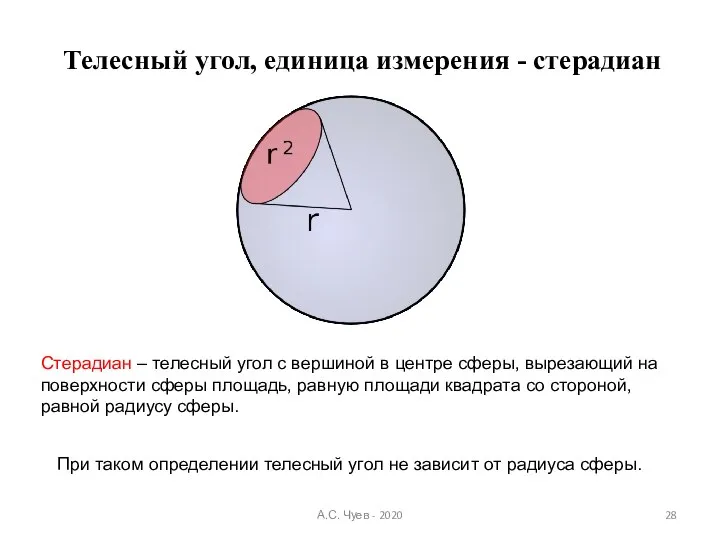
- 28. Телесный угол, единица измерения - стерадиан При таком определении телесный угол не зависит от радиуса сферы.
- 29. Плоский угол, единица измерения - радиан 1 радиан — центральный угол, длина дуги которого равна радиусу
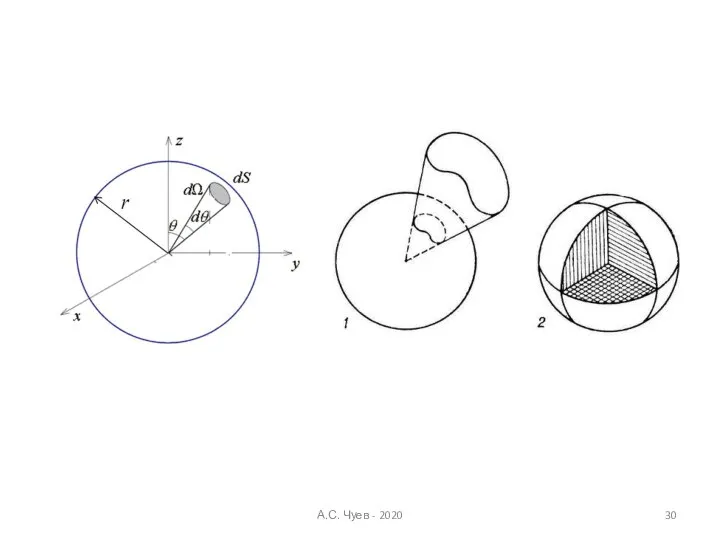
- 30. А.С. Чуев - 2020
- 31. А.С. Чуев - 2020
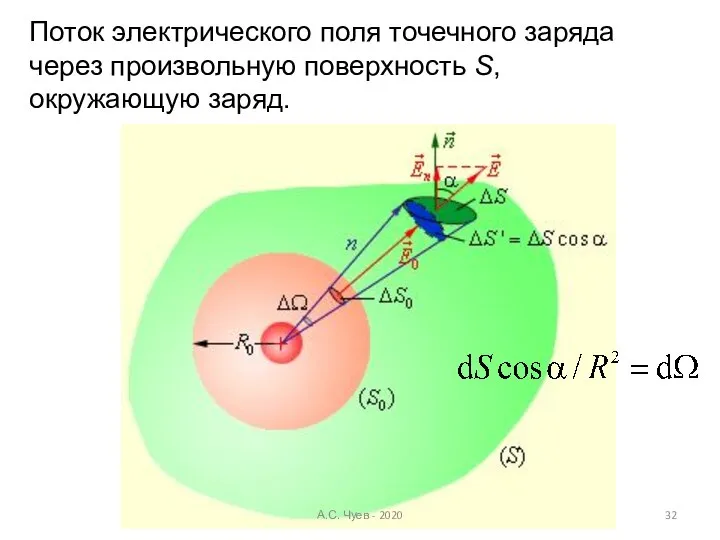
- 32. Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд. А.С. Чуев - 2020
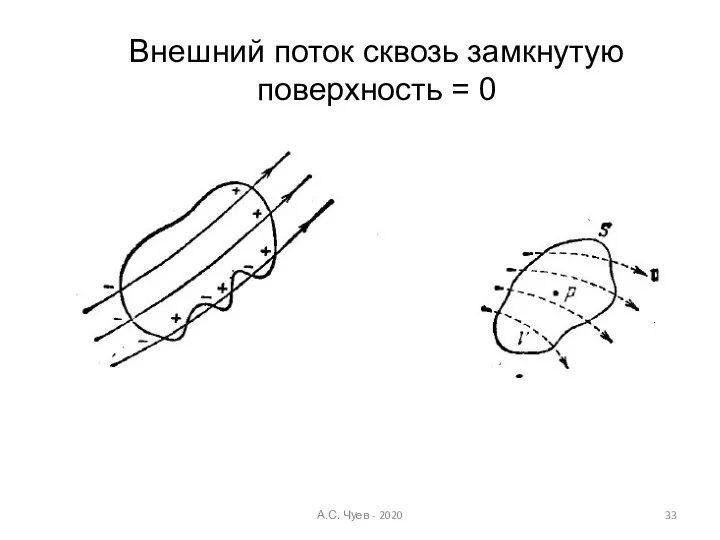
- 33. Внешний поток сквозь замкнутую поверхность = 0 А.С. Чуев - 2020
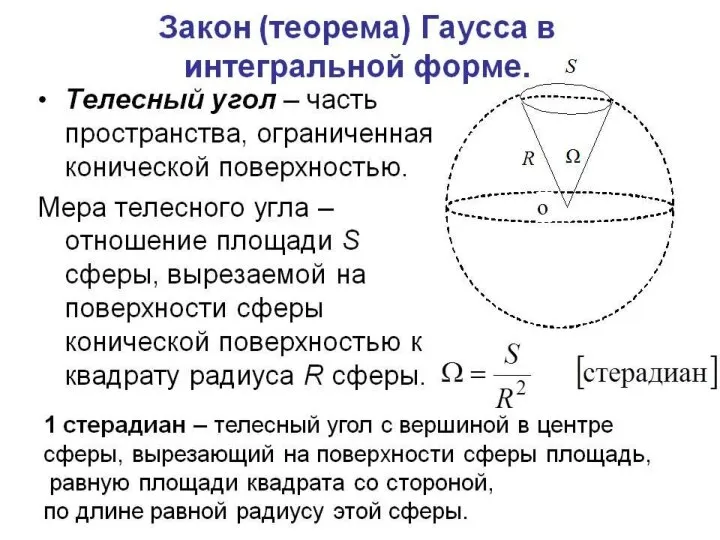
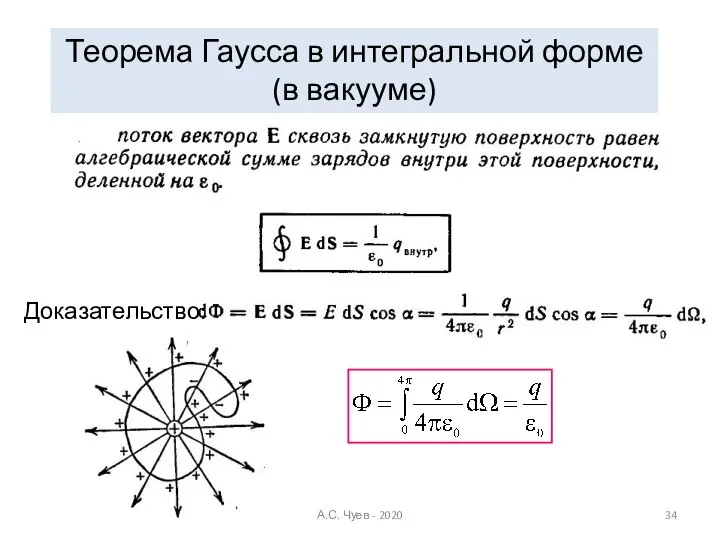
- 34. Теорема Гаусса в интегральной форме (в вакууме) Доказательство: А.С. Чуев - 2020
- 35. Теорема Гаусса в дифференциальной форме (в вакууме). Уравнение Пуассона А.С. Чуев - 2020 Уравнение Пуассона
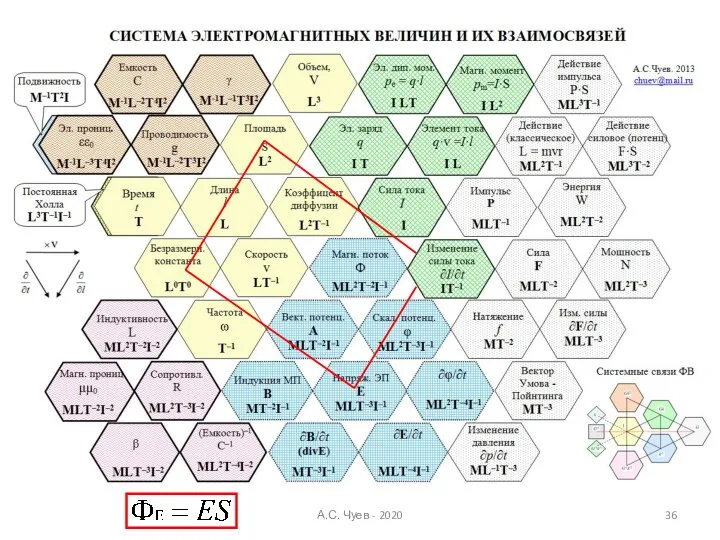
- 36. А.С. Чуев - 2020
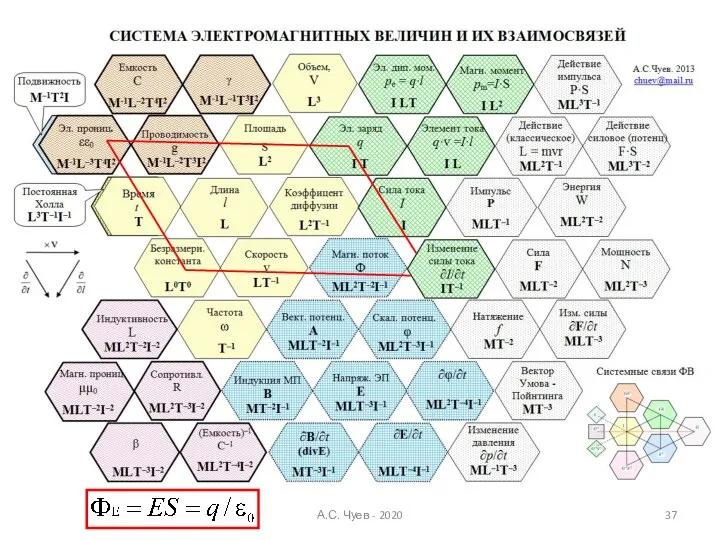
- 37. А.С. Чуев - 2020
- 38. А.С. Чуев - 2020
- 39. Приводимые далее примеры рассмотреть самостоятельно А.С. Чуев - 2020
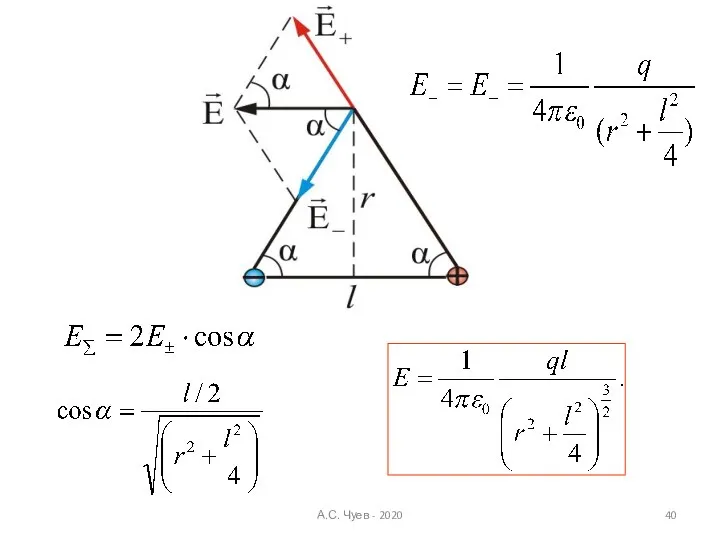
- 40. А.С. Чуев - 2020
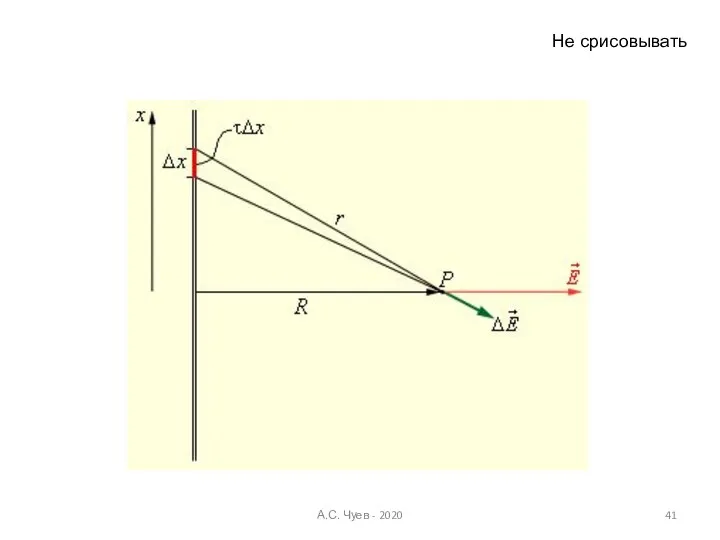
- 41. Не срисовывать А.С. Чуев - 2020
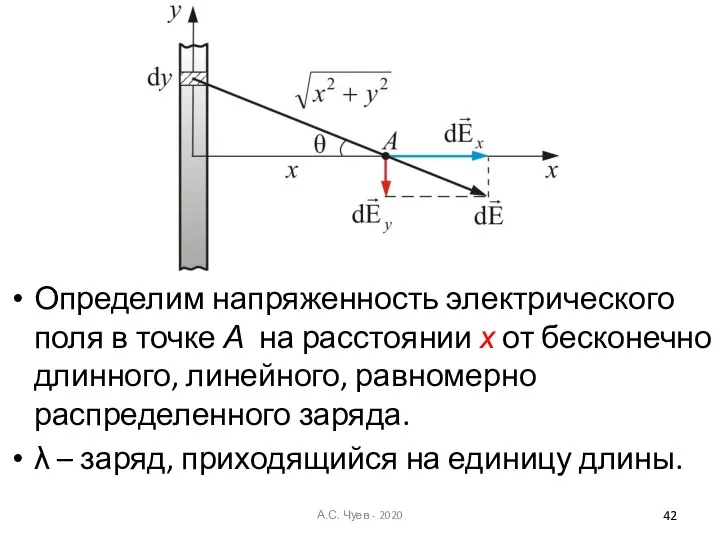
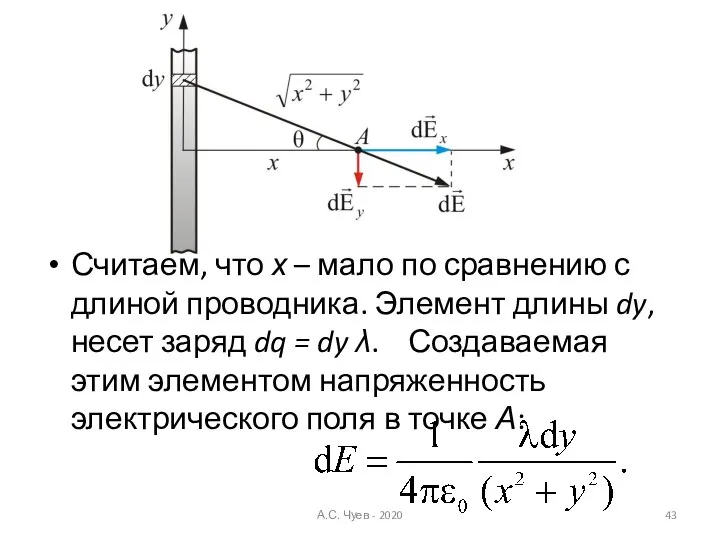
- 42. Определим напряженность электрического поля в точке А на расстоянии х от бесконечно длинного, линейного, равномерно распределенного
- 43. Считаем, что х – мало по сравнению с длиной проводника. Элемент длины dy, несет заряд dq
- 44. Вектор имеет проекции dEx и dEy причем Т.к. проводник бесконечно длинный, а задача симметричная, то у
- 45. Тогда Теперь выразим y через θ. Т.к. то С учетом: А.С. Чуев - 2020
- 46. Напряженность электрического поля от линейно распределенных зарядов (заряженной нити) изменяется обратно пропорционально расстоянию до заряда. А.С.
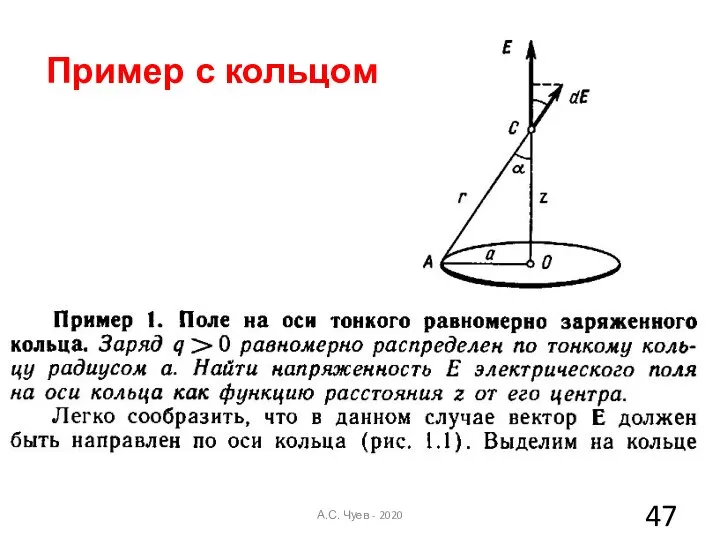
- 47. Пример с кольцом А.С. Чуев - 2020
- 48. А.С. Чуев - 2020
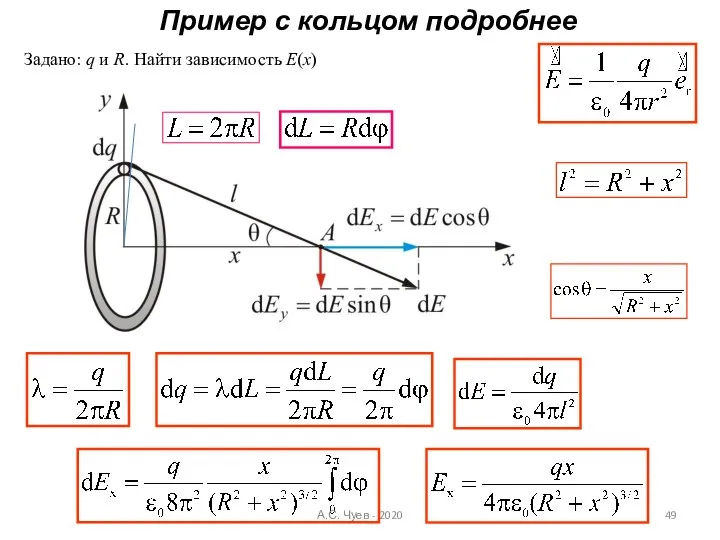
- 49. Пример с кольцом подробнее Задано: q и R. Найти зависимость Е(х) А.С. Чуев - 2020
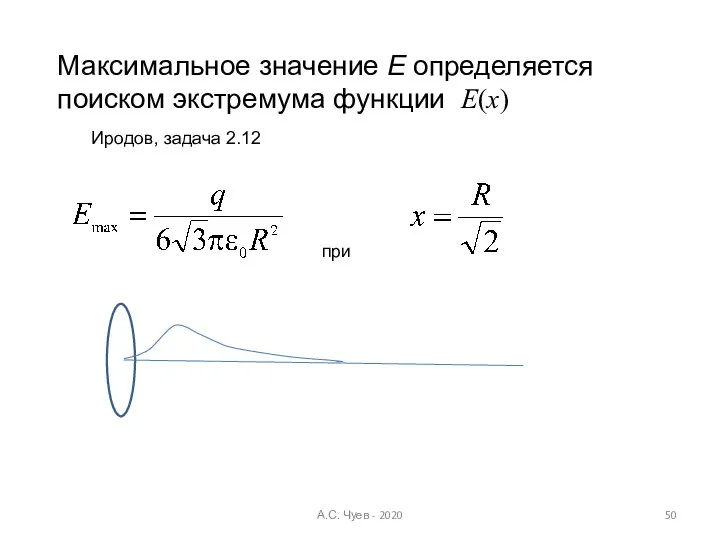
- 50. Максимальное значение Е определяется поиском экстремума функции Е(х) при Иродов, задача 2.12 А.С. Чуев - 2020
- 51. МАТЕРИЯ ВЕЩЕСТВО ПОЛЕ ФИЗ. ВАКУУМ (Т, Ж, Г) Электромагнитная теория З, П Э, М, Гр. Вирт.
- 52. Факультативно А.С. Чуев - 2020
- 54. Скачать презентацию


















 Программа для решения физических задач
Программа для решения физических задач Lect_4
Lect_4 Сила. Силы в природе и Работа. Мощность
Сила. Силы в природе и Работа. Мощность Сложение двух сил, направленных по одной прямой. Равнодействующая сила
Сложение двух сил, направленных по одной прямой. Равнодействующая сила Основы термодинамики. Лекция 2.3
Основы термодинамики. Лекция 2.3 Бизнес идея: Практичный домкрат для автомобилей
Бизнес идея: Практичный домкрат для автомобилей Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Применение ядерного оружия
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Применение ядерного оружия Молекулярно-кинетическая теория (презентации к системе уроков)
Молекулярно-кинетическая теория (презентации к системе уроков) Викторина по физике 9 класс
Викторина по физике 9 класс Электромагнетизм
Электромагнетизм Презентация на тему Электростатика
Презентация на тему Электростатика  Принцип Даламбера для материальной точки. Лекция 2
Принцип Даламбера для материальной точки. Лекция 2 Презентация на тему Альберт Эйнштейн
Презентация на тему Альберт Эйнштейн  Классификация магнитных материалов специального назначения. (Лекция 8)
Классификация магнитных материалов специального назначения. (Лекция 8) Визначення температури спалаху та самозапалення нафтопродуктів. Практичне заняття № 6
Визначення температури спалаху та самозапалення нафтопродуктів. Практичне заняття № 6 Механическая работа
Механическая работа Измерение количества и расхода жидкости и газа в практике горно-буровых работ
Измерение количества и расхода жидкости и газа в практике горно-буровых работ Польза и вред электризации
Польза и вред электризации Газовые законы
Газовые законы Приборы и методы экспериментальной физики
Приборы и методы экспериментальной физики Энергия. 7 класс
Энергия. 7 класс Волновые процессы
Волновые процессы Презентация на тему Криволинейное движение
Презентация на тему Криволинейное движение  Перемещение при равномерном прямолинейном движении
Перемещение при равномерном прямолинейном движении Аристотель, его вклад в развитие механики
Аристотель, его вклад в развитие механики Закон Ома для участка цепи. Самостоятельная работа
Закон Ома для участка цепи. Самостоятельная работа Суд над атомом. Мультимедийный урок
Суд над атомом. Мультимедийный урок Специальная теория относительности. Постулаты теории относительности
Специальная теория относительности. Постулаты теории относительности