Механические колебания. Физика. 9 класс

Механические колебания - это движения, которые точно или приблизительно повторяются через определённый интервал времени.
Колебания – один из самых распространённых процессов в природе и технике.

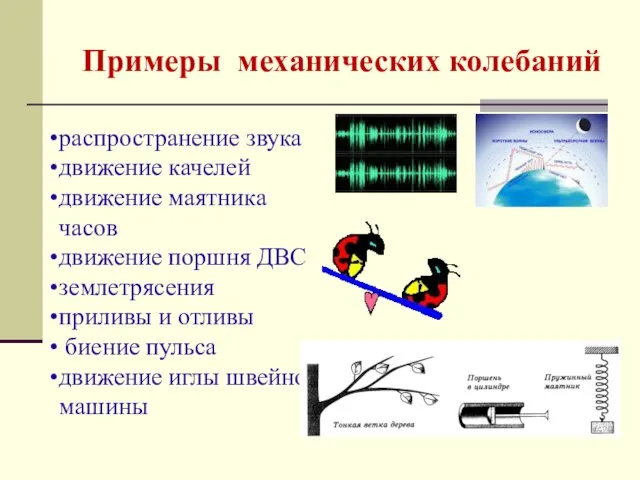
Примеры механических колебаний
распространение звука
движение качелей
движение маятника часов
движение поршня ДВС
землетрясения
приливы и отливы
биение пульса
движение иглы швейной машины

Механические колебания
Свободные колебания –
происходят в системе под действием внутренних сил, после выведения её из положения равновесия, благодаря начальному запасу энергии
Вынужденные –
это колебания, происходящие под действием внешних периодически изменяющихся сил

Условия существования свободных колебаний
а) наличие у колебательной системы положения устойчивого равновесия (ПУР);
б) равнодействующая сил после выведения системы из положения равновесия направлена к ПУР (появление возвращающей силы);
в) ПУР тело проходит по инерции;
г) силы трения (сопротивления) в системе малы.

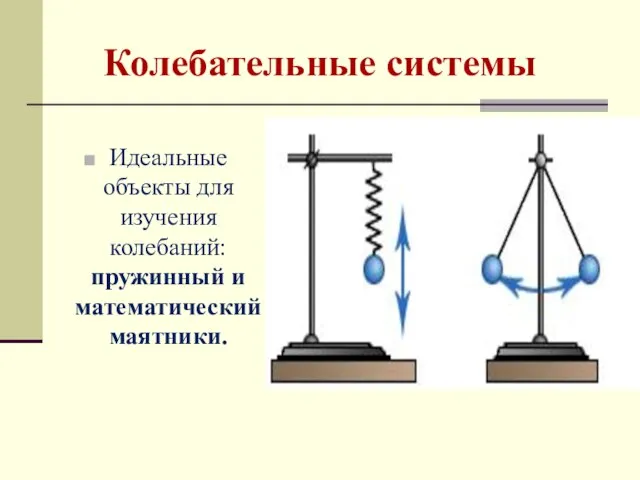
Колебательные системы – это системы (совокупность тел), способные совершать свободные колебания
Колебательные системы
качели;
тело на нити;
тело на пружине;
струна гитары
Системы, не являющиеся
колебательными
игла швейной машины;
поршень ДВС

Колебательные системы
Идеальные объекты для изучения колебаний: пружинный и математический маятники.

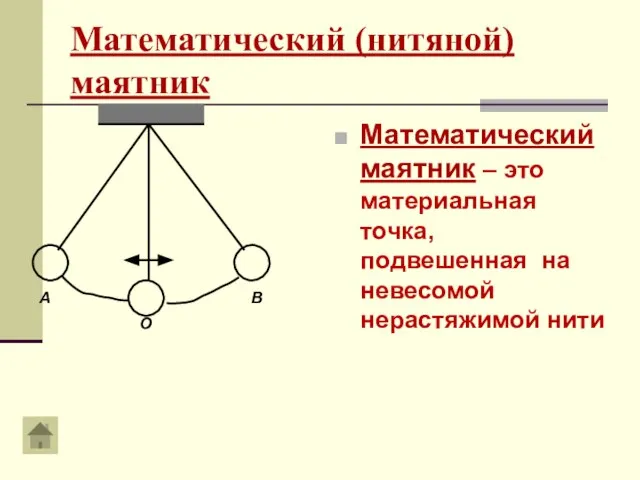
Математический (нитяной) маятник
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити
А
В
О

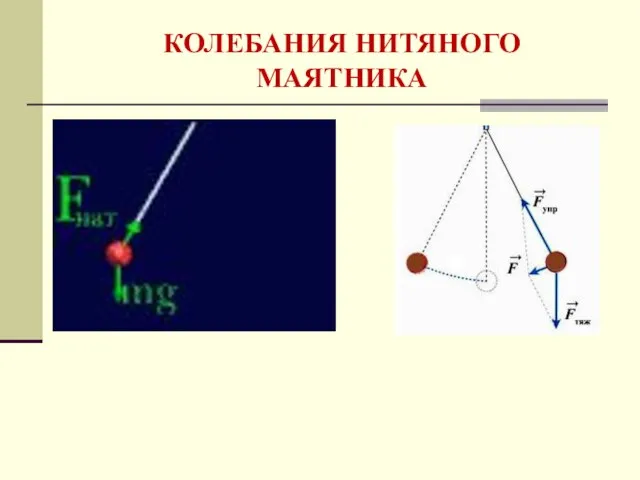
КОЛЕБАНИЯ НИТЯНОГО МАЯТНИКА

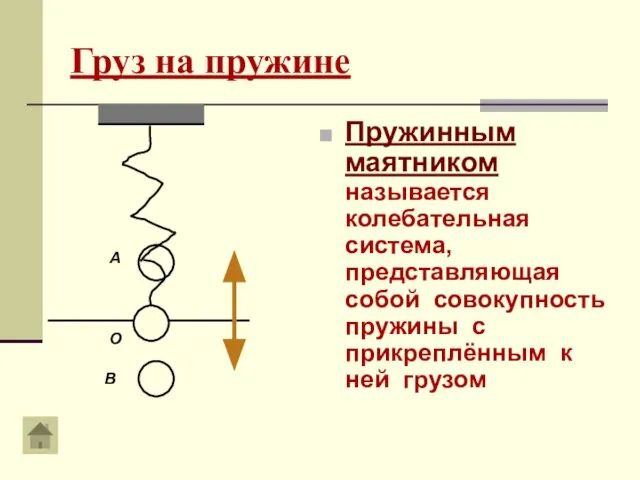
Груз на пружине
Пружинным маятником называется колебательная система, представляющая собой совокупность пружины с прикреплённым к ней грузом
В
А
О

Величины, характеризующие
колебательное движение:

х – смещение (отклонение) от положения равновесия
[х]=1м
А или хmax – амплитуда колебаний: максимальное смещение от положения равновесия
[A]=[xmax] =1м
ω («омега») - циклическая частота колебаний.
ω = 2πν = 2π/T
[ω]=1рад/с=1с¯¹

Т – период колебаний: промежуток времени, в течение которого совершается одно полное колебание.
ν («ню») - частота колебаний: число колебаний
в единицу времени.
Т =t/N ν=N/t
N – количество колебаний
t – общее время для N колебаний
Т=1/ν ν=1/Т
[Т]=1с [ν ]=1/с=1с¯¹=1Гц
1 Гц – это одно колебание в секунду.
Примерно с такой частотой бьётся человеческое сердце.

Формулы периодов колебаний
Период колебаний математического маятника
Зависит от:
Длины нити маятника (l)
Ускорения свободного падения в данном месте (g)
НЕ ЗАВИСИТ ОТ МАССЫ
Период колебаний пружинного маятника
Зависит от:
Массы груза (m)
Жёсткости пружины (k)