Линии влияния усилий в фермах

Построение линий влияния усилий (продольных сил)
в стержнях ферм
Особенность линий влияния продольных сил в стержнях ферм –
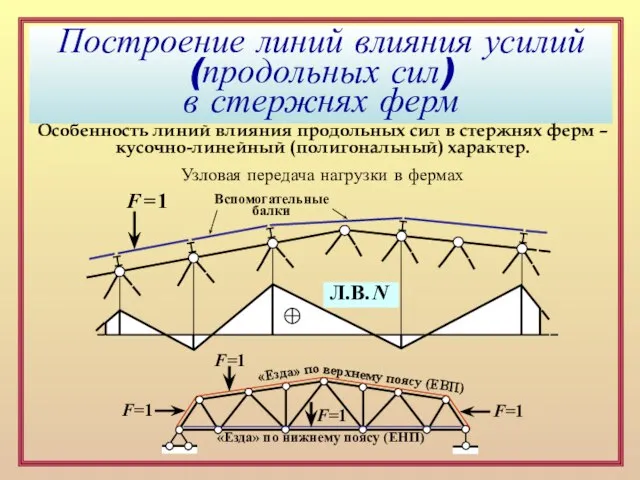
кусочно-линейный (полигональный) характер.
Узловая передача нагрузки в фермах
Вспомогательные
балки
F = 1
Л.В. N
F=1
F=1
«Езда» по
верхнему поясу (ЕВП)
«Езда» по нижнему поясу (ЕНП)
F=1
F=1

Построение
линий влияния
усилий в стержнях ферм
статическим методом
(типовые задачи для ферм
с простыми решётками)

F = 1
х
а
а
а
а
а
а
а
а
h/2
h/2
Требуется построить
линии влияния усилий
в стержнях поясов и решётки
простой балочной фермы
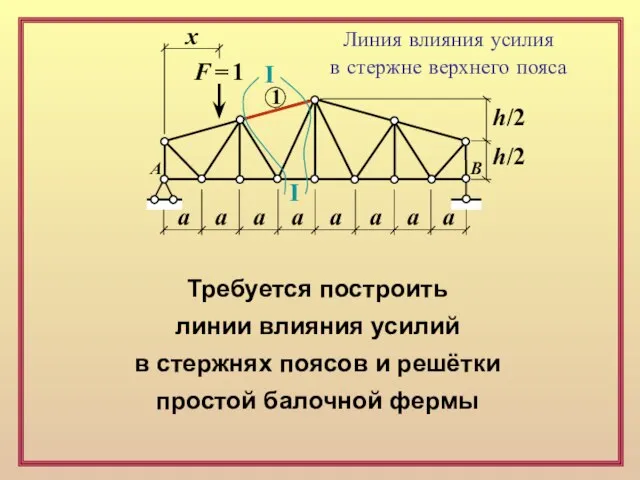
Линия влияния усилия
в стержне верхнего пояса
1
I
I
A
B

F = 1
х
а
а
а
а
а
а
а
а
h/2
h/2
Линия влияния усилия
в стержне верхнего пояса
1
I
I
Груз F = 1 слева от сечения I-I:
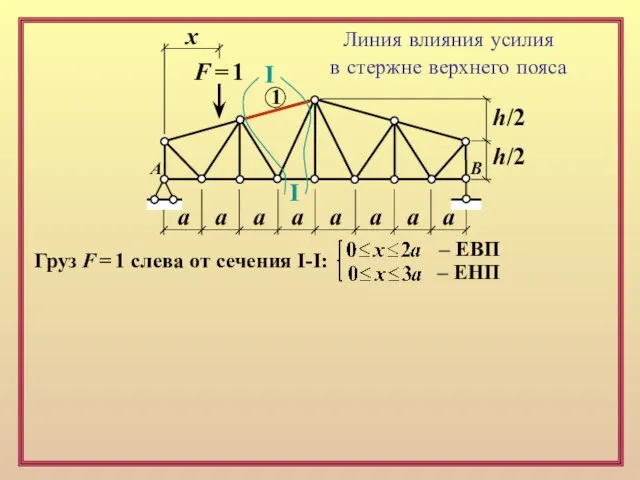
– ЕВП
– ЕНП
A
B

F = 1
х
а
а
а
а
а
а
а
а
h/2
h/2
Линия влияния усилия
в стержне верхнего пояса
1
I
I
Груз F = 1 слева от сечения I-I:
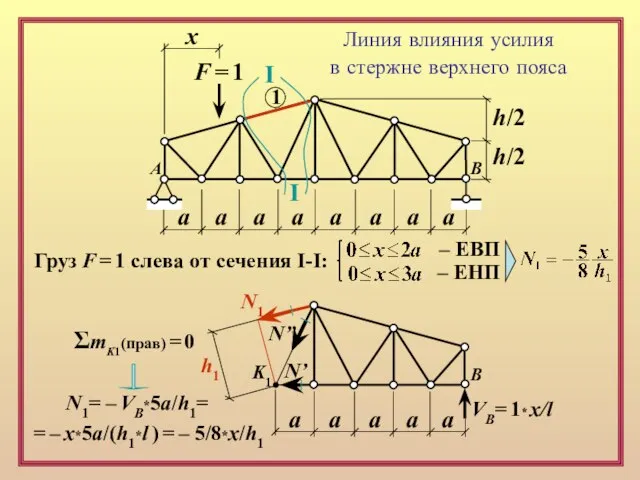
– ЕВП
– ЕНП
а
а
а
а
а
В
VB= 1* x/l
N’
N”
N1
K1
h1
ΣmK1(прав) = 0
N1= – VB*5a/h1=
= – x*5a/(h1*l ) = – 5/8*x/h1
A
B

F = 1
х
а
а
а
а
а
а
а
а
h/2
h/2
Линия влияния усилия
в стержне верхнего пояса
1
I
I
Груз F = 1 слева от сечения I-I:
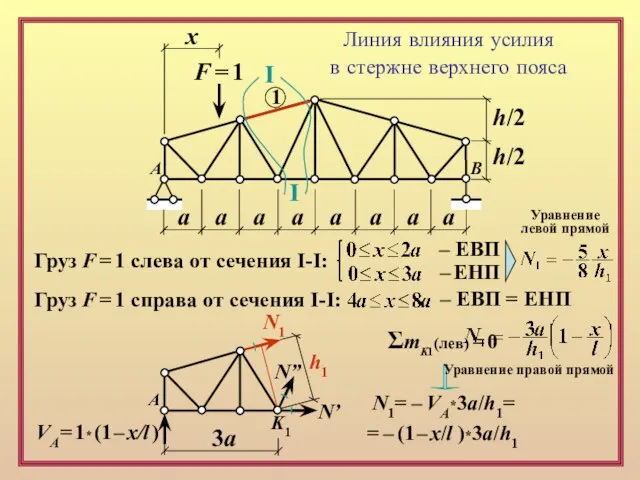
– ЕВП
– ЕНП
Груз F = 1 справа от сечения I-I:
– ЕВП = ЕНП
VА= 1* (1 – x/l )
h1
A
B
A
N’
N1
N”
K1
3а
ΣmK1(лев) = 0
N1= – VA*3a/h1=
= – (1 – x/l )*3a/h1
Уравнение
левой прямой
Уравнение правой прямой

F = 1
х
а
а
а
а
а
а
а
а
h/2
h/2
Линия влияния усилия
в стержне верхнего пояса
1
I
I
Груз F = 1 слева от сечения I-I:
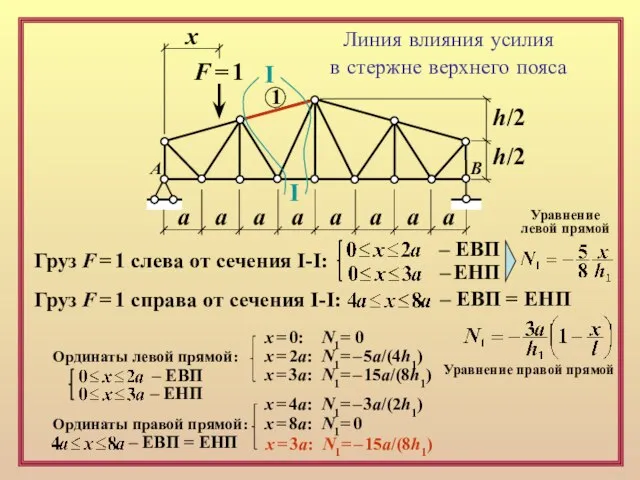
– ЕВП
– ЕНП
Груз F = 1 справа от сечения I-I:
– ЕВП = ЕНП
A
B
Уравнение
левой прямой
Уравнение правой прямой
Ординаты левой прямой:
x = 0: N1= 0
x = 2a: N1= – 5a/(4h1)
x = 3a: N1= – 15a/(8h1)
Ординаты правой прямой:
x = 4a: N1= – 3a/(2h1)
x = 8a: N1= 0
x = 3a: N1= – 15a/(8h1)
– ЕВП
– ЕНП
– ЕВП = ЕНП

F = 1
х
а
а
а
а
а
а
а
а
h/2
h/2
Линия влияния усилия
в стержне верхнего пояса
1
I
I
A
B
Уравнение
левой прямой
Уравнение правой прямой
Ординаты левой прямой:
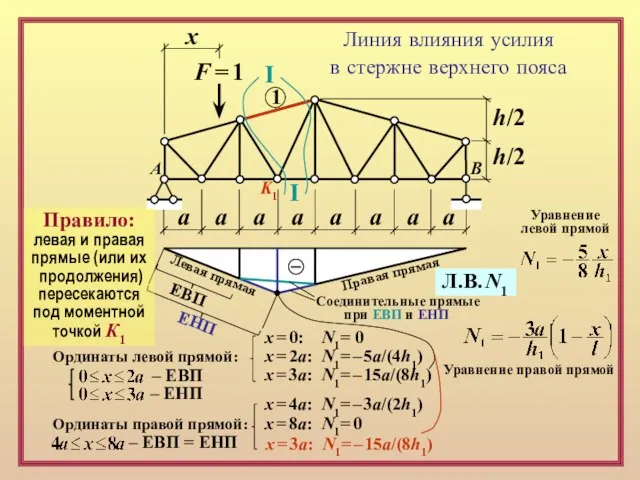
x = 0: N1= 0
x = 2a: N1= – 5a/(4h1)
x = 3a: N1= – 15a/(8h1)
Ординаты правой прямой:
x = 4a: N1= – 3a/(2h1)
x = 8a: N1= 0
x = 3a: N1= – 15a/(8h1)
– ЕВП
– ЕНП
– ЕВП = ЕНП
K1
Левая прямая
Правая прямая
ЕВП
ЕНП
Соединительные прямые
при ЕВП и ЕНП
Правило:
левая и правая
прямые (или их
продолжения)
пересекаются
под моментной
точкой К1
Л.В. N1

F = 1
х
а
а
а
а
а
а
а
а
h/2
h/2
Линия влияния усилия
в стержне нижнего пояса
2
II
II
A
B
Уравнение
левой прямой
Уравнение правой прямой
K2
Груз F = 1 слева
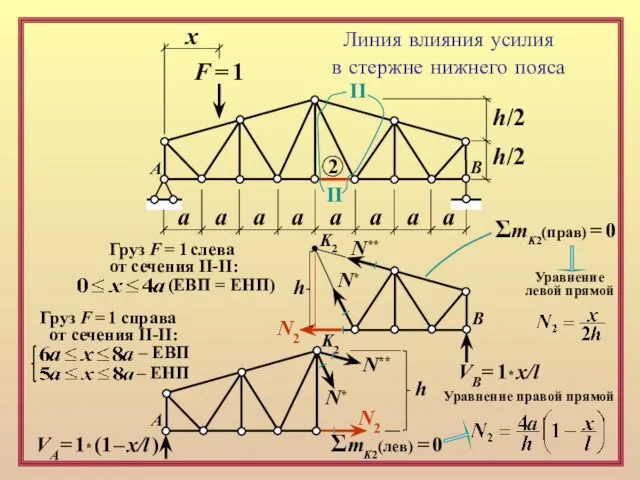
от сечения II-II:
(ЕВП = ЕНП)
B
VB= 1* x/l
Груз F = 1 справа
от сечения II-II:
– ЕВП
– ЕНП
N2
N**
N*
h
ΣmK2(прав) = 0
N2
N**
N*
K2
VА= 1* (1 – x/l )
h
ΣmK2(лев) = 0
A

F = 1
х
а
а
а
а
а
а
а
а
h/2
h/2
Линия влияния усилия
в стержне нижнего пояса
2
II
II
A
B
Уравнение
левой прямой
Уравнение правой прямой
x = 5a: N2 = 3a/(2h)
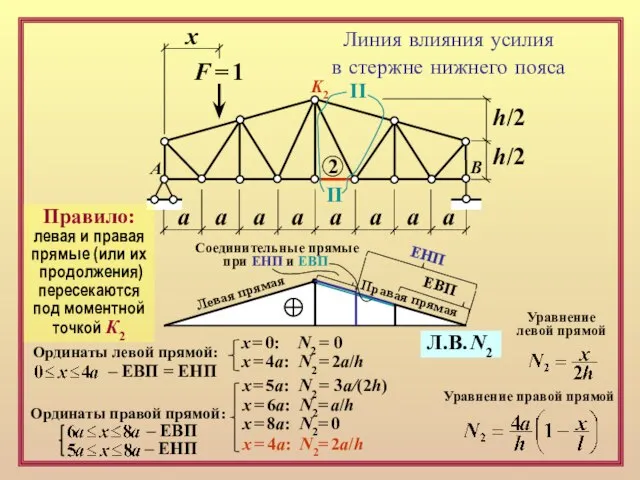
x = 6a: N2= a/h
x = 8a: N2= 0
x = 4a: N2= 2a/h
Ординаты левой прямой:
Ординаты правой прямой:
– ЕВП
– ЕНП
– ЕВП = ЕНП
Правая прямая
Левая прямая
ЕВП
ЕНП
Соединительные прямые
при ЕНП и ЕВП
Л.В. N2
x = 0: N2 = 0
x = 4a: N2 = 2a/h
Правило:
левая и правая
прямые (или их
продолжения)
пересекаются
под моментной
точкой К2
K2

F = 1
х
а
а
а
а
а
а
а
а
h/2
h/2
Линия влияния усилия
в стержне решётки – раскосе
3
III
III
A
B
Уравнение
левой прямой:
Уравнение
правой прямой:
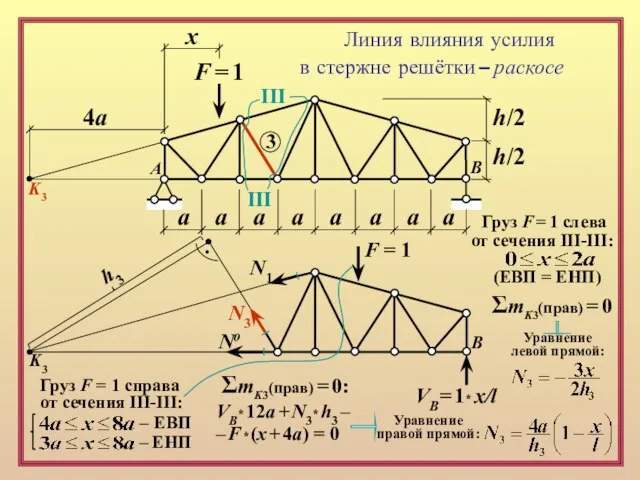
K3
4а
Груз F = 1 слева
от сечения III-III:
(ЕВП = ЕНП)
B
Груз F = 1 справа
от сечения III-III:
– ЕВП
– ЕНП
N3
No
h3
ΣmK3(прав) = 0
K3
VB= 1* x/l
N1
F = 1
ΣmK3(прав) = 0:
VB* 12a + N3* h3 –
– F * (x + 4a) = 0

F = 1
х
а
а
а
а
а
а
а
а
h/2
h/2
3
III
III
A
B
Уравнение
левой прямой
Уравнение правой прямой
x = 3a: N3= 5a/(2h3)
x = 4a: N3= 2a/h3
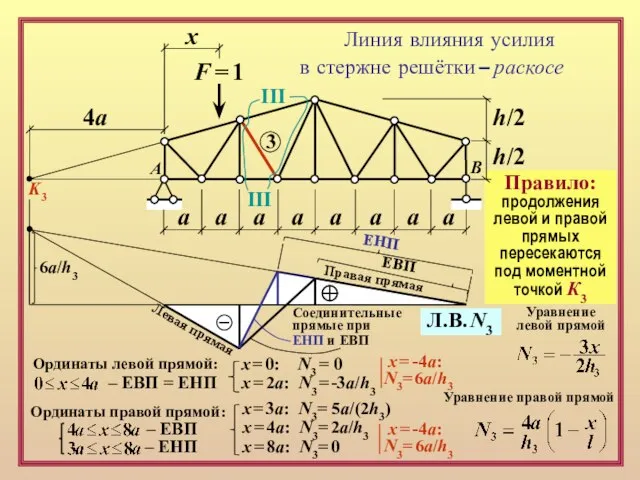
x = 8a: N3= 0
x = -4a:
N3= 6a/h3
Ординаты левой прямой:
Ординаты правой прямой:
– ЕВП
– ЕНП
– ЕВП = ЕНП
Правая прямая
Левая прямая
ЕВП
ЕНП
Соединительныепрямые при
ЕНП и ЕВП
Л.В. N3
x = 0: N3 = 0
x = 2a: N3 = -3a/h3
Правило:
продолжения левой и правой
прямых
пересекаются
под моментной
точкой К3
K3
4а
x = -4a:
N3= 6a/h3
6a/h3
Линия влияния усилия
в стержне решётки – раскосе

F = 1
х
а
а
а
а
а
а
а
а
h/2
h/2
Линия влияния усилия
в одиночной стойке
(подвеске)
4
IV
A
B
Случай 1:
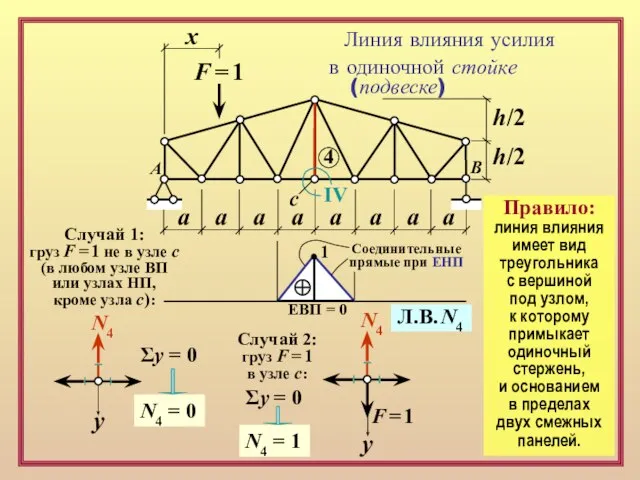
груз F = 1 не в узле с
(в любом узле ВП
или узлах НП,
кроме узла с):
ЕВП = 0
Соединительные
прямые при ЕНП
Л.В. N4
Правило:
линия влияния
имеет вид треугольника
с вершиной
под узлом,
к которому
примыкает одиночный стержень,
и основанием
в пределах
двух смежных
панелей.
c
N4
у
Σy = 0
N4 = 0
Случай 2:
груз F = 1
в узле с:
у
N4
F = 1
Σy = 0
N4 = 1
1

F = 1
1
2
3
4
х
Типовые линии влияния усилий в стержнях ферм
с простыми решётками
K1
K2
K3
5 П р а в и л а :
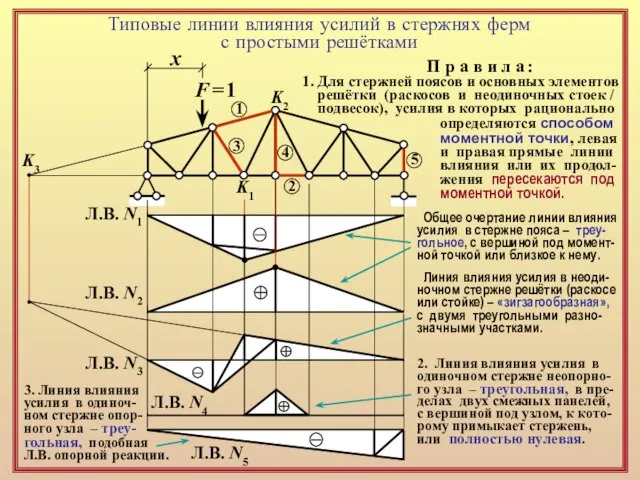
1. Для стержней поясов и основных элементов
решётки (раскосов и неодиночных стоек /
подвесок), усилия в которых рационально
определяются способом
моментной точки, левая
и правая прямые линии
влияния или их продол-
жения пересекаются под
моментной точкой.
Л.В. N1
Л.В. N2
Общее очертание линии влияния
усилия в стержне пояса – треу-
гольное, с вершиной под момент-
ной точкой или близкое к нему.
Линия влияния усилия в неоди-
ночном стержне решётки (раскосе
или стойке) – «зигзагообразная»,
с двумя треугольными разно-
значными участками.
Л.В. N3
2. Линия влияния усилия в
одиночном стержне неопорно-го узла – треугольная, в пре-делах двух смежных панелей,
с вершиной под узлом, к кото- рому примыкает стержень,
или полностью нулевая.
Л.В. N4
Л.В. N5
3. Линия влияния
усилия в одиноч-
ном стержне опор-
ного узла – треу-
гольная, подобная
Л.В. опорной реакции.

Построение
линий влияния
усилий в стержнях ферм
кинематическим методом
Основная расчётная формула:
Определение
δF (x) и δN
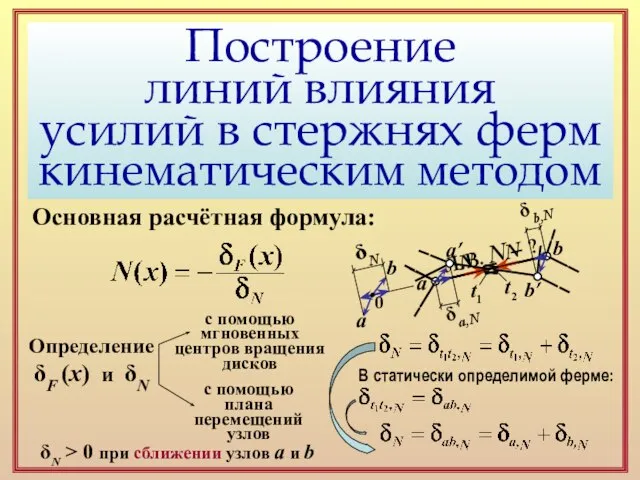
с помощью
мгновенных
центров вращения
дисков
с помощью
плана
перемещений
узлов
Л.В. N – ?
a
b
a’
b’
N
N
t1
t2
В статически определимой ферме:
δa,N
δb,N
a
b
0
δN
δN > 0 при сближении узлов a и b

Способ мгновенных центров вращения дисков в построении
л.в. усилий в стержнях ферм кинематическим методом
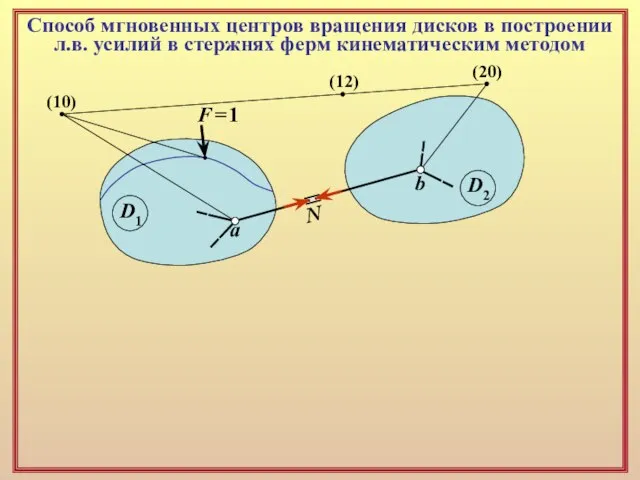
D1
D2
a
b
N
F = 1
(10)
(12)
(20)

Способ мгновенных центров вращения дисков в построении
л.в. усилий в стержнях ферм кинематическим методом
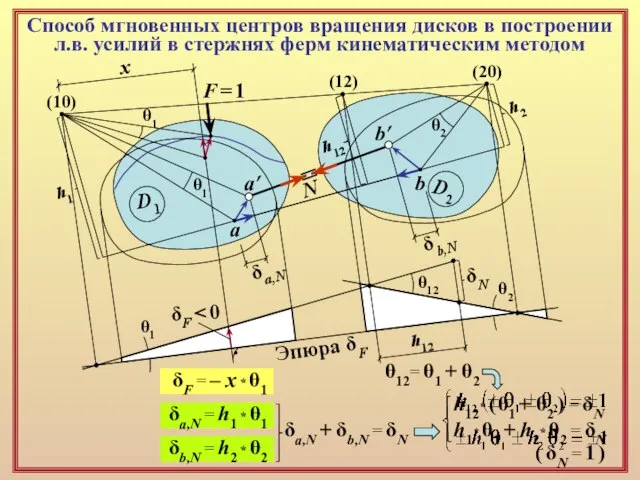
D1
D2
a
b
F = 1
(10)
(12)
(20)
N
a’
b’
θ1
θ1
θ2
θ2
θ1
Эпюра δF
δF < 0
x
δF = – x * θ1
δa,N
δb,N
δa,N = h1 * θ1
δb,N = h2 * θ2
h1
h2
δa,N + δb,N = δN
h1* θ1 + h2* θ2 = δN
h12
h12
θ12
δN
θ12= θ1 + θ2
h12* ( θ1 + θ2 ) = δN
( δN = 1 )

Способ мгновенных центров вращения дисков в построении
л.в. усилий в стержнях ферм кинематическим методом
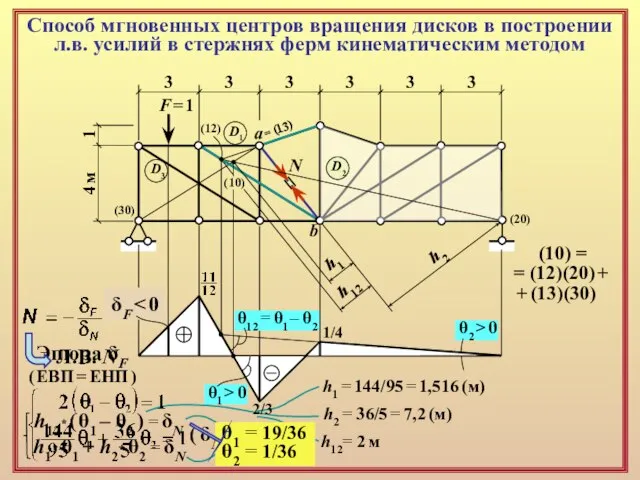
3
3
3
3
3
3
4 м
N
a
b
F = 1
D1
D3
D2
(20)
(12)
(30)
= (13)
(10)
1
(10) =
= (12)(20) +
+ (13)(30)
h2
h1
h12
h1 = 144/95 = 1,516 (м)
h2 = 36/5 = 7,2 (м)
h12= 2 м
Эпюра δF
δF < 0
θ12 = θ1 – θ2
θ1 > 0
θ2 > 0
h1* θ1 + h2* θ2 = δN
h12* ( θ1 – θ2 ) = δN
( δN = 1 )
θ1 = 19/36
θ2 = 1/36
1/4
2/3
Л.В. N
( ЕВП = ЕНП )

Способ мгновенных центров вращения дисков в построении
л.в. усилий в стержнях ферм кинематическим методом
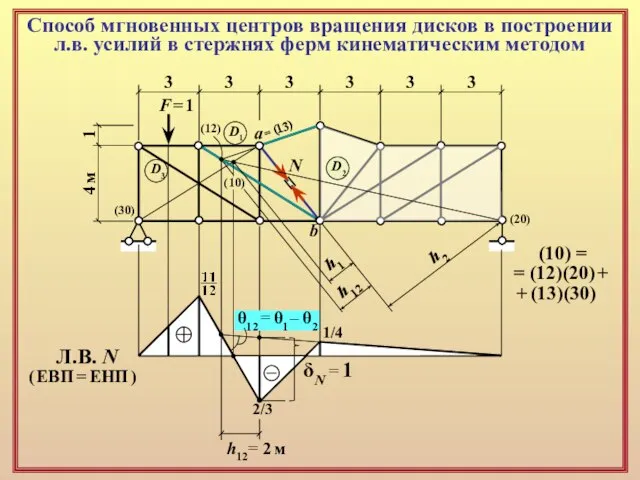
3
3
3
3
3
3
4 м
N
a
b
F = 1
D1
D3
D2
(20)
(12)
(30)
= (13)
(10)
1
(10) =
= (12)(20) +
+ (13)(30)
h2
h1
h12
h12= 2 м
θ12 = θ1 – θ2
δN = 1
1/4
2/3
Л.В. N
( ЕВП = ЕНП )

Построение л.в. усилия в стержне фермы кинематическим методом с помощью плана перемещений узлов
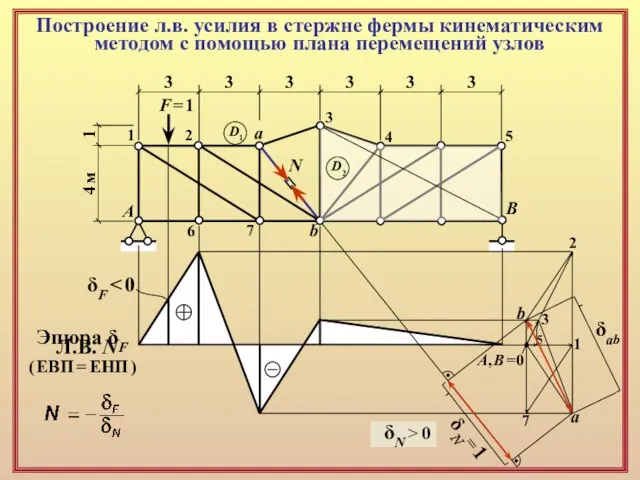
3
3
3
3
3
3
4 м
N
a
b
F = 1
D1
D2
В
1
1
δN = 1
Л.В. N
( ЕВП = ЕНП )
А
2
3
4
5
6
7
1
7
а
b
3
5
2
A, B = 0
δF < 0
δab
δN > 0
Эпюра δF

К о н т р о л ь н ы е в о п р о с ы
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 22» )
1. Особенности линий влияния усилий в стержнях ферм. ( 2 )
2. Учёт узловой передачи нагрузки при построении линий влияния усилий в стержнях ферм. ( 2 )
3. Как получаются соединительные прямые на линии влияния усилия в стержне фермы при езде поверху и понизу? ( 2 ) 3. Как получаются соединительные прямые на линии влияния усилия в стержне фермы при езде поверху и понизу? ( 2 ) ( 9 ) 3. Как получаются соединительные прямые на линии влияния усилия в стержне фермы при езде поверху и понизу? ( 2 ) ( 9 ) ( 11 ) 3. Как получаются соединительные прямые на линии влияния усилия в стержне фермы при езде поверху и понизу? ( 2 ) ( 9 ) ( 11 ) ( 13 ) 3. Как получаются соединительные прямые на линии влияния усилия в стержне фермы при езде поверху и понизу? ( 2 ) ( 9 ) ( 11 ) ( 13 ) ( 14 )
4. Типовое правило построения линии влияния усилия в стержне фермы, определяемого способом вырезания узла. ( 14 ) 4. Типовое правило построения линии влияния усилия в стержне фермы, определяемого способом вырезания узла. ( 14 ) ( 15 )
5. Типовое правило построения линии влияния усилия в стержне фермы, определяемого способом моментной точки. ( 9 ) 5. Типовое правило построения линии влияния усилия в стержне фермы, определяемого способом моментной точки. ( 9 ) ( 11 ) 5. Типовое правило построения линии влияния усилия в стержне фермы, определяемого способом моментной точки. ( 9 ) ( 11 ) ( 13 ) 5. Типовое правило построения линии влияния усилия в стержне фермы, определяемого способом моментной точки. ( 9 ) ( 11 ) ( 13 ) ( 15 )
6. Типовое правило построения линии влияния усилия в стержне фермы, определяемого способом проекций. ( самостоятельно – как частный случай способа Риттера )
7. Чему равна разность ординат линии влияния усилия в стойке раскосной решётки при езде поверху и понизу? ( самостоятельно )
8. Изобразить типовую линию влияния усилия в поясе балочной фермы. ( 9 ) 8. Изобразить типовую линию влияния усилия в поясе балочной фермы. ( 9 ) ( 11 )
9. Изобразить типовую линию влияния усилия в раскосе балочной фермы
с простой решёткой. ( 13 )
10. Изобразить типовую линию влияния усилия в раскосе балочной фермы
с параллельными поясами и треугольной решёткой. ( самостоятельно )
11. Изобразить типовую линию влияния усилия в стойке трапецеидальной балочной фермы. ( самостоятельно )
12. Изобразить линию влияния усилия в стойке треугольной фермы с раскосной решёткой. ( самостоятельно )
13. Изобразить линию влияния усилия в одиночном стержне трёхстержневого узла частного вида. ( 14 )
_______________________________________
*) Только в режиме «Показ слайдов»