Содержание
- 2. Механические колебания и волны – раздел механики, изучающий особый вид движения – колебания, а так же
- 3. Колебания Колебания – это движения или процессы, которые точно или приблизительно повторяются через определенные интервалы времени.
- 4. Гармонические колебания – это колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или
- 5. Период гармонических колебаний равен: T = 2π/ω . Число колебаний в единицу времени называется частотой колебаний
- 7. При гармонических колебаниях вдоль оси ОХ координата тела изменяется по закону: х = 0,9·cos 5t (м).
- 8. При гармонических колебаниях вдоль оси Ох координата тела изменяется по закону х = 0,9 sin3t (м).
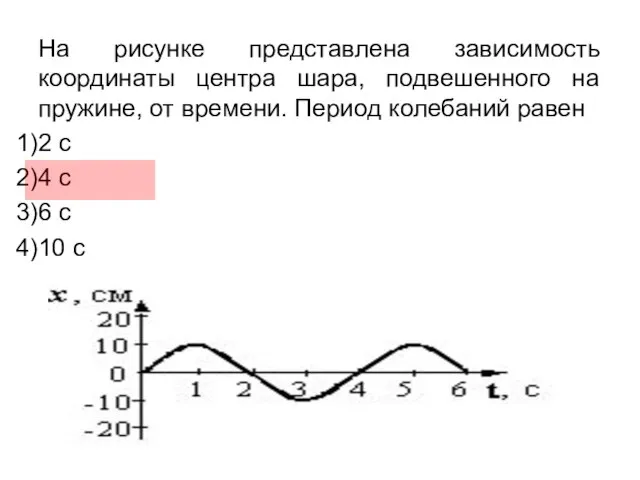
- 9. На рисунке представлена зависимость координаты центра шара, подвешенного на пружине, от времени. Период колебаний равен 2
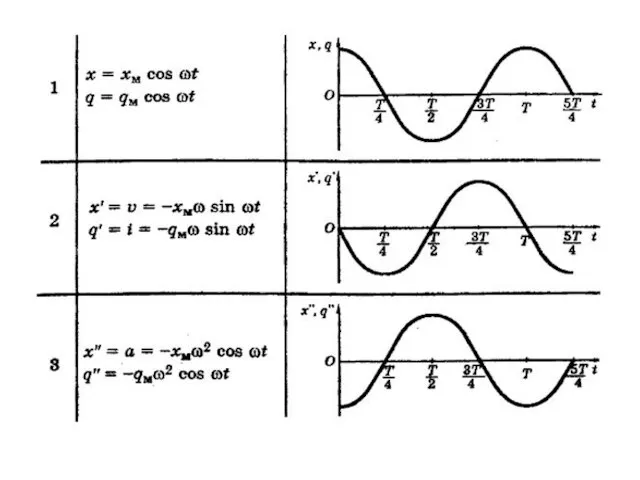
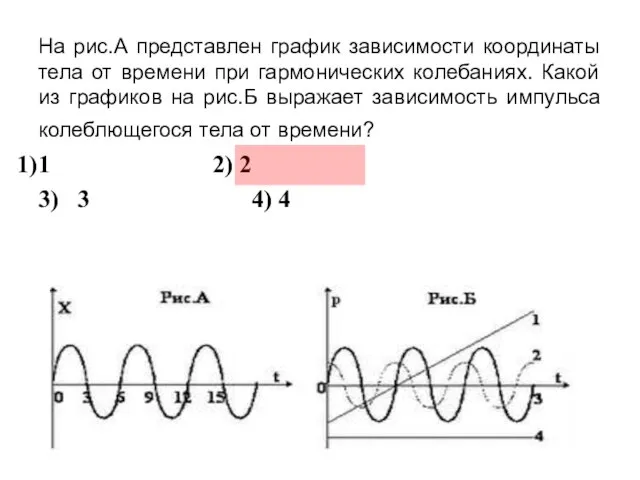
- 10. На рис.А представлен график зависимости координаты тела от времени при гармонических колебаниях. Какой из графиков на
- 11. Виды колебаний Свободные Вынужденные Автоколебания
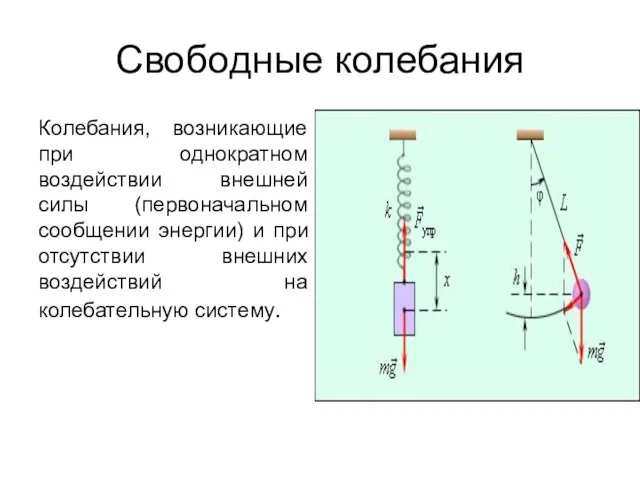
- 12. Свободные колебания Колебания, возникающие при однократном воздействии внешней силы (первоначальном сообщении энергии) и при отсутствии внешних
- 13. Условия возникновения свободных колебаний 1. Колебательная система должна иметь положение устойчивого равновесия. 2. При выведении системы
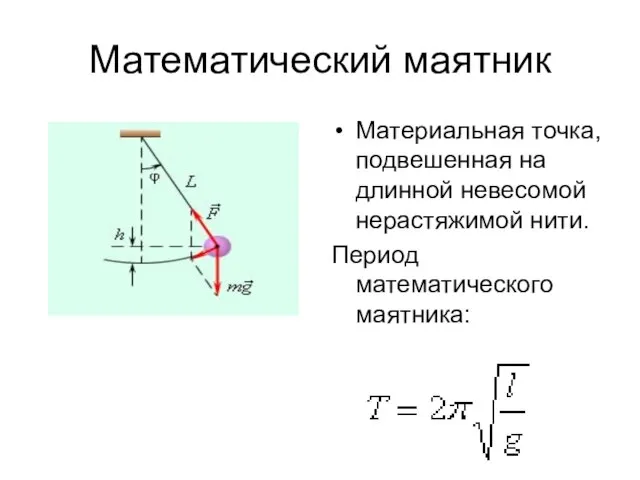
- 14. Математический маятник Материальная точка, подвешенная на длинной невесомой нерастяжимой нити. Период математического маятника:
- 15. Как изменится период колебаний математического, если его длину уменьшить в 2 раза, а массу увеличить в
- 16. Какова частота колебаний математического маятника длиной 2,5м ? 1) 2 Гц 2) 1 Гц 3) 0,32
- 17. Массу груза математического маятника уменьшили в 2 раза. Как при этом изменился период колебаний маятника? 1)Увеличился
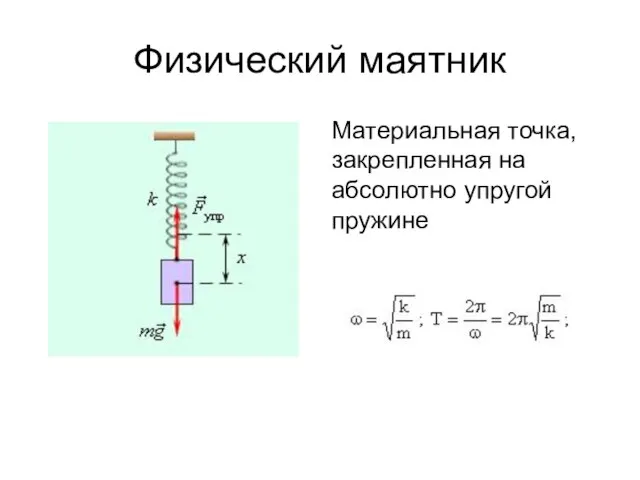
- 18. Физический маятник Материальная точка, закрепленная на абсолютно упругой пружине
- 19. Каков период колебаний груза на пружинке, если он из верхнего крайнего положения проходит путь до нижнего
- 20. К пружине жесткостью 40 Н/м подвешен груз массой 0,1 кг. Период свободных колебаний этого пружинного маятника
- 21. Груз массой 0,16 кг, подвешенный на пружине, совершает гармонические колебания. Какой должна быть масса груза, чтобы
- 22. Какова должна быть жесткость пружины маятника, чтобы периоды колебаний тела массой 200 г этого маятника и
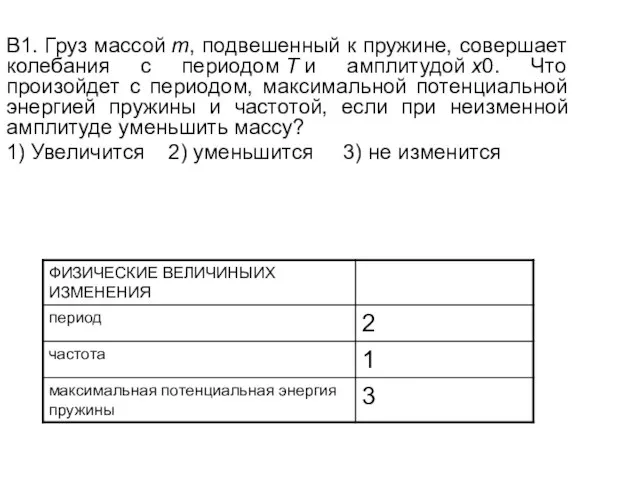
- 23. В1. Груз массой m, подвешенный к пружине, совершает колебания с периодом T и амплитудой x0. Что
- 24. Вынужденные колебания Колебания, возникающие под действием внешних, периодически изменяющихся сил (при периодическом поступлении энергии извне к
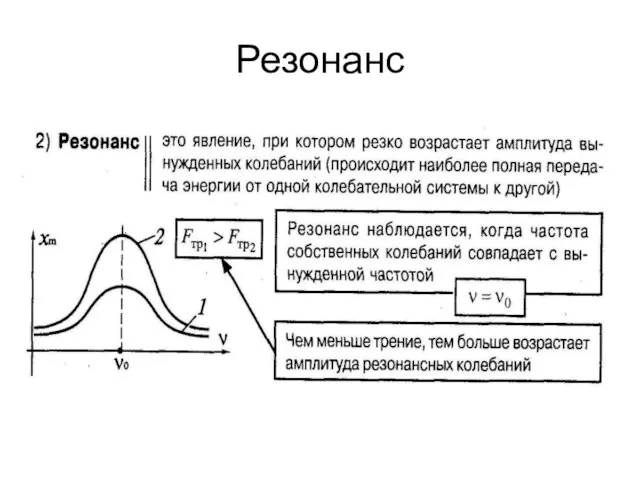
- 25. Резонанс
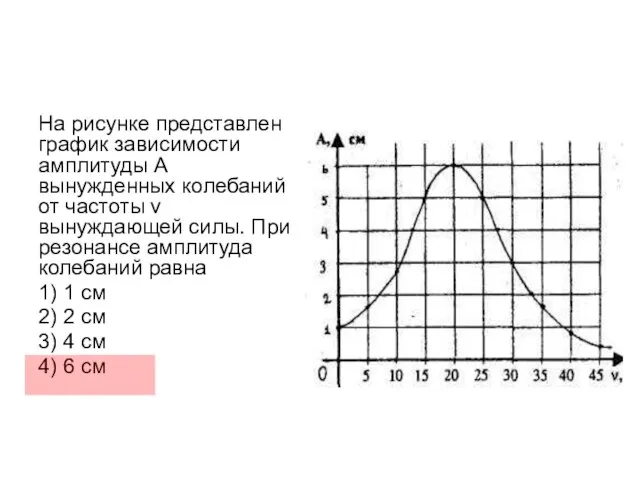
- 26. На рисунке представлен график зависимости амплитуды А вынужденных колебаний от частоты v вынуждающей силы. При резонансе
- 28. Скачать презентацию
















 Испарение и факторы, влияющие на него
Испарение и факторы, влияющие на него Основные понятия электродинамики
Основные понятия электродинамики Презентация (4)
Презентация (4) Устройство легкового автомобиля и величина тормозного пути транспортного средства
Устройство легкового автомобиля и величина тормозного пути транспортного средства Призматический фасонный резец
Призматический фасонный резец Техническое обслуживание и текущий ремонт сцепления, коробки передач, карданной передачи
Техническое обслуживание и текущий ремонт сцепления, коробки передач, карданной передачи Презентация на тему Солнце (11 класс)
Презентация на тему Солнце (11 класс)  Термодинамика
Термодинамика Давление газа. Уравнение состояния идеального газа. Изопроцессы
Давление газа. Уравнение состояния идеального газа. Изопроцессы Оценка одновременно нескольких параметров
Оценка одновременно нескольких параметров Элементы гидроаэромеханики (продолжение)
Элементы гидроаэромеханики (продолжение) Амперметр. Измерение силы тока в цепи
Амперметр. Измерение силы тока в цепи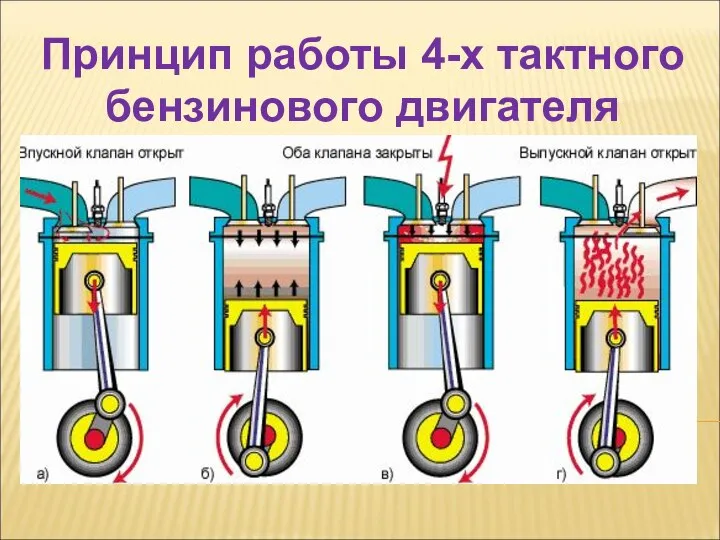 Принцип работы 4-х тактного бензинового двигателя
Принцип работы 4-х тактного бензинового двигателя Температура
Температура Циркониевые трубки
Циркониевые трубки Абрикосов Алексей Алексеевич
Абрикосов Алексей Алексеевич Методы исследование структуры. Часть 1
Методы исследование структуры. Часть 1 Общие теоремы динамики
Общие теоремы динамики Взаимодействие проводников с током
Взаимодействие проводников с током Законы физики в стихах
Законы физики в стихах Графит и алмаз. Кристаллы
Графит и алмаз. Кристаллы Тормозные рычажные передачи
Тормозные рычажные передачи Сила Архимеда 7 класс - Презентация_
Сила Архимеда 7 класс - Презентация_ Энергия магнитного поля. Объемная плотность энергии
Энергия магнитного поля. Объемная плотность энергии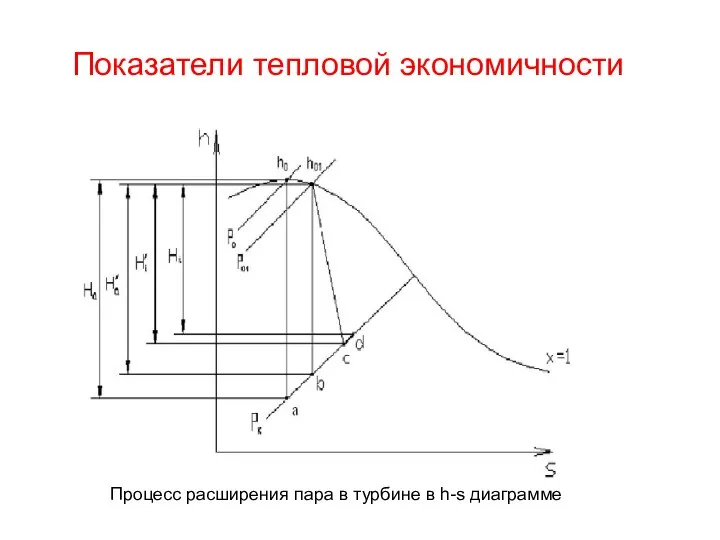 Показатели тепловой экономичности
Показатели тепловой экономичности Рентгеновское излучение их природа, и свойства
Рентгеновское излучение их природа, и свойства Чувствительность взрывчатых систем к внешним воздействиям
Чувствительность взрывчатых систем к внешним воздействиям Термодинамика. Лекция 6
Термодинамика. Лекция 6