Содержание
- 2. Простейшие примеры течений вязкой жидкости u0 I. Движение жидкости между движущимися плоскостями x y ux=u(y,t) Течение
- 3. Граничные условия: u=u0 при y=h a=u0 /h u=0 при y=0 b=0 Решение: Распределение скоростей между пластинами
- 4. II. Движение жидкости между неподвижными плоскостями x y ux=u(y,t) h 0 Жидкость течет за счет силы
- 5. Граничные условия: u x=0 при y=0, y=h b=0 Решение с учетом гран. условий Течение имеет параболический
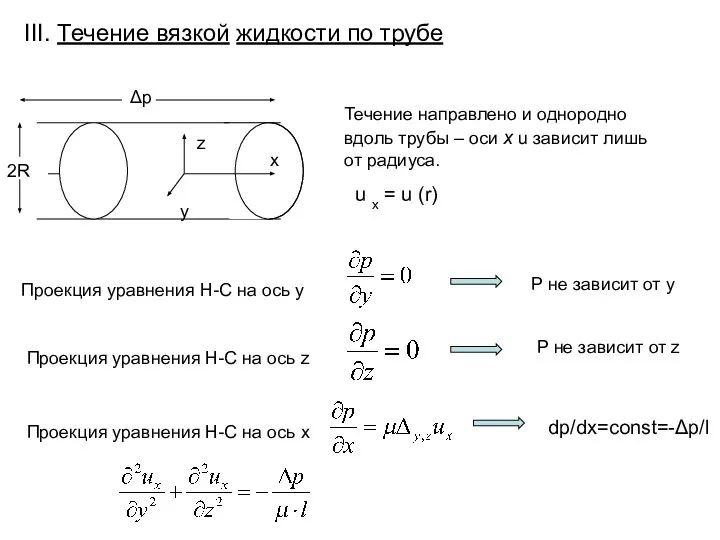
- 6. III. Течение вязкой жидкости по трубе Δp Течение направлено и однородно вдоль трубы – оси x
- 7. III а. Течение вязкой жидкости по трубе кругового сечения Скорость конечна во всем сечении трубы, поэтому
- 8. III б. Течение вязкой жидкости по трубе эллиптического сечения Труба эллиптического сечения y z Общее решение
- 9. Предельный переход от трубы эллиптического сечения к параллельным плоскостям (b>>a) Было решение для двух плоскостей y
- 10. Уравнение Навье –Стокса с потенциальными силами Стационарное течение жидкости Умножаем скалярно на элемент линии тока, dr
- 12. Скачать презентацию








 Естественная радиоактивность. Закон радиоактивного распада
Естественная радиоактивность. Закон радиоактивного распада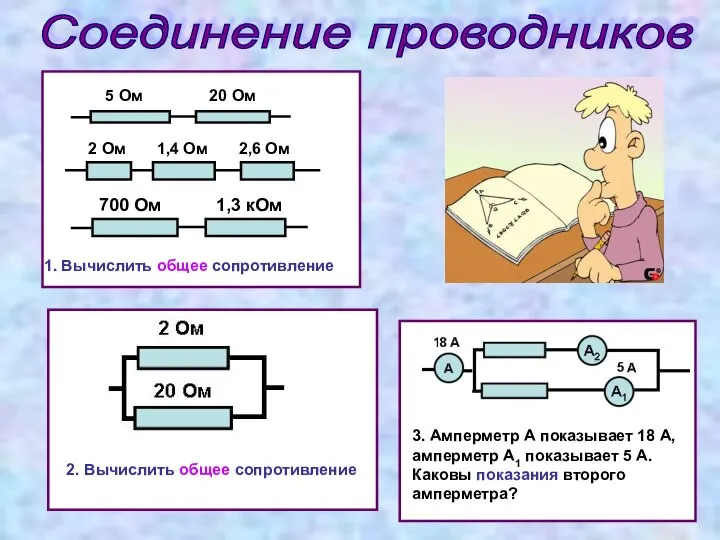 Соединение проводников
Соединение проводников Индикаторы напряжения
Индикаторы напряжения Работа и мощность в цепях постоянного тока. Закон Джоуля-Ленца. КПД источника в цепи постоянного тока
Работа и мощность в цепях постоянного тока. Закон Джоуля-Ленца. КПД источника в цепи постоянного тока Радиационное излучение
Радиационное излучение Работа потенциальных сил. Законы сохранения в механике
Работа потенциальных сил. Законы сохранения в механике Классификация навигационных систем. Параметры движения в пространстве
Классификация навигационных систем. Параметры движения в пространстве Расчет массы и объема тела по его плотности
Расчет массы и объема тела по его плотности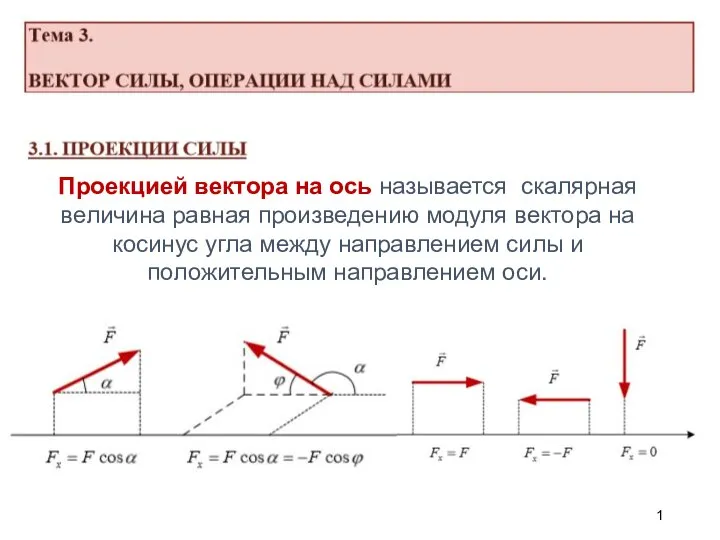 Вектор силы, операции над силами
Вектор силы, операции над силами Разновидности уравнений материальных балансов ВТП. Материальные расчеты идеальных ВТП
Разновидности уравнений материальных балансов ВТП. Материальные расчеты идеальных ВТП Бинокль. Оптические и оптикоэлектронные приборы и комплексы
Бинокль. Оптические и оптикоэлектронные приборы и комплексы Найдем правильную дорогу
Найдем правильную дорогу 8_
8_ Перший закон термодинаміки
Перший закон термодинаміки Применение физических законов при решении задач по астрофизике
Применение физических законов при решении задач по астрофизике История тепловых двигателей
История тепловых двигателей Спектры
Спектры Модели атомов. Опыт Резерфорда
Модели атомов. Опыт Резерфорда Блок цилиндров двигателя
Блок цилиндров двигателя Расчет сопротивления электрических цепей
Расчет сопротивления электрических цепей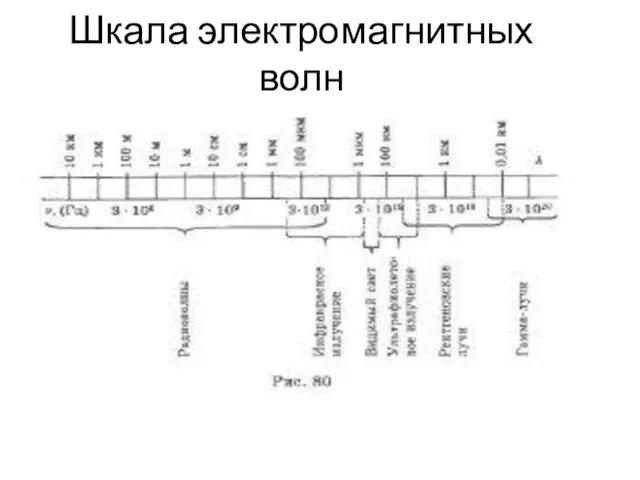 Шкала электромагнитных волн
Шкала электромагнитных волн Построение изображеия в линзах и формула линзы. 11 класс
Построение изображеия в линзах и формула линзы. 11 класс Давление. Обобщение
Давление. Обобщение Протоколы квантового распределения ключей
Протоколы квантового распределения ключей Рефрактометрия. Преломление света
Рефрактометрия. Преломление света Молекулярная физика и термодинамика
Молекулярная физика и термодинамика Что такое мощность
Что такое мощность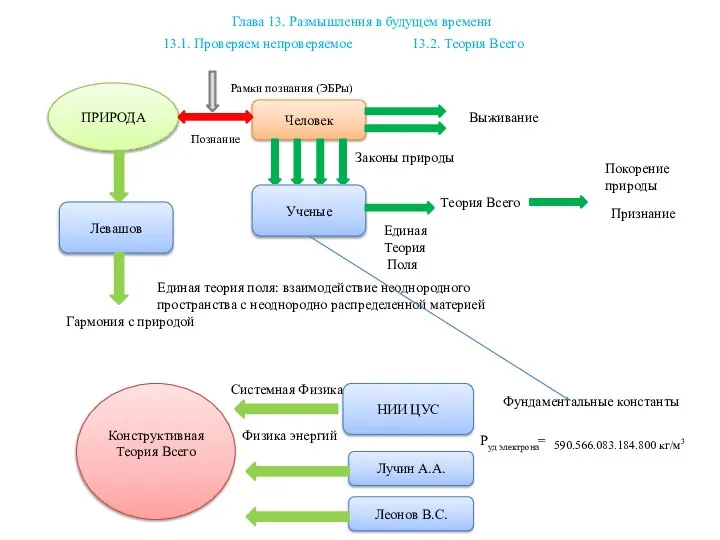 Размышления в будущем времени
Размышления в будущем времени