Слайд 2§16. Механические волны
I. Уравнение бегущей волны
Волна — ФЯ — любое распространяющееся в
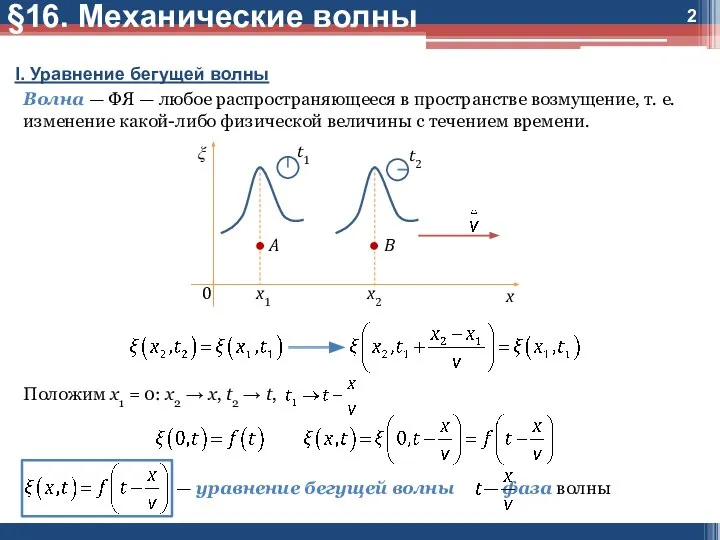
пространстве возмущение, т. е. изменение какой-либо физической величины с течением времени.
Положим x1 = 0: x2 → x, t2 → t,
— уравнение бегущей волны — фаза волны
Слайд 3§16. Механические волны
II. Волновой фронт
Волновой фронт (волновая поверхность) — геометрическое место точек,
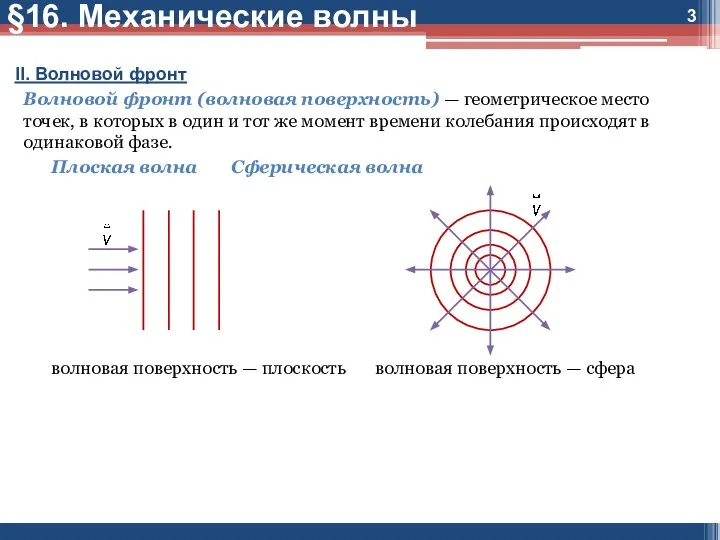
в которых в один и тот же момент времени колебания происходят в одинаковой фазе.
Плоская волна Сферическая волна
волновая поверхность — плоскость волновая поверхность — сфера
Слайд 4§16. Механические волны
III. Гармоническая волна
Гармоническая (монохроматическая, синусоидальная) волна — ФЯ — распространение

гармонических колебаний в пространстве.
Уравнение гармонических колебаний
Уравнение бегущей волны
— уравнение плоской бегущей гармонической волны
Слайд 5§16. Механические волны
Характеристики гармонической волны
Скорость v
Начальная фаза φ0
Циклическая частота ω
Период
Частота
Амплитуда A

— максимальное значение колеблющейся ФВ
Длина волны — ФВ — расстояние, которое волна проходит за время одного полного колебания:
Волновое число
Слайд 6§16. Механические волны
«Мгновенная фотография» гармонической волны
Уравнение бегущей гармонической волны в общем случае
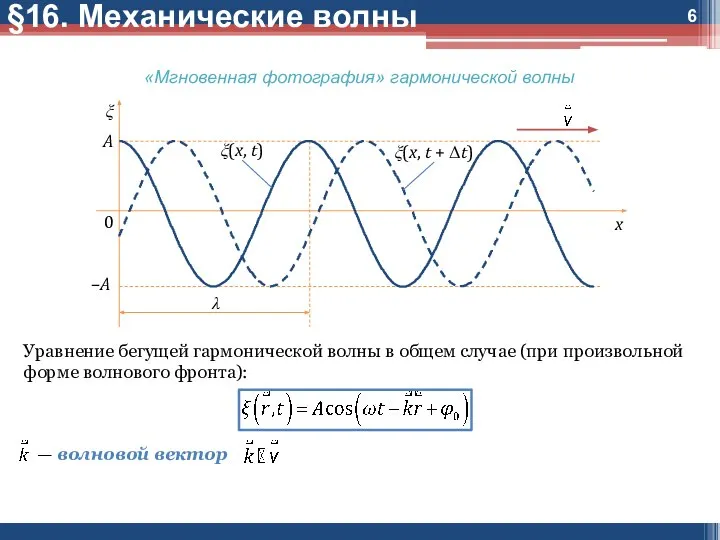
(при произвольной форме волнового фронта):
— волновой вектор





 Вимірювальні прилади
Вимірювальні прилади Опыты дома
Опыты дома Правило смещения
Правило смещения Схема гідросистеми натягу гусениць
Схема гідросистеми натягу гусениць Введение в волновую оптику. Способы наблюдения интерференции. Лекция 2с 9 (2)
Введение в волновую оптику. Способы наблюдения интерференции. Лекция 2с 9 (2) Материалы, применяемые в электронике, электротехнике и радиотехнике
Материалы, применяемые в электронике, электротехнике и радиотехнике Отчёт о проверке автомобиля
Отчёт о проверке автомобиля Давление жидкостей и газов. Игра – путешествие
Давление жидкостей и газов. Игра – путешествие МФТИ 5 вариант. Подготовка к ЕГЭ
МФТИ 5 вариант. Подготовка к ЕГЭ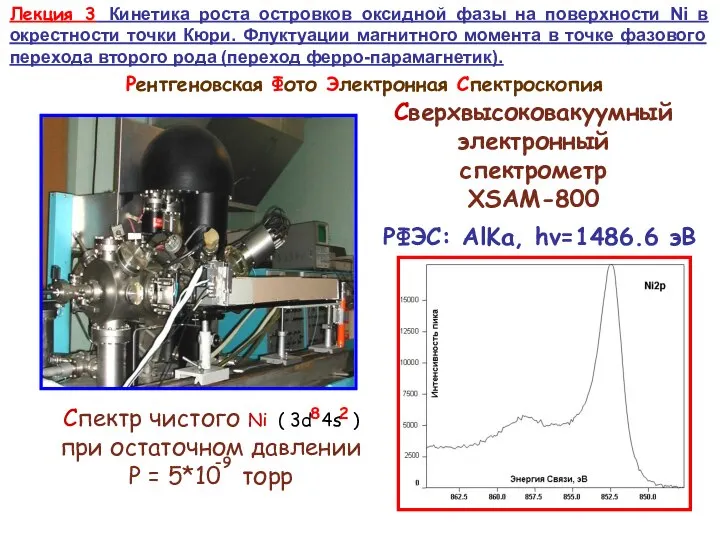 Кинетика роста островков оксидной фазы на поверхности Ni в окрестности точки Кюри
Кинетика роста островков оксидной фазы на поверхности Ni в окрестности точки Кюри Роль домашнего демонстрационного физического эксперимента в формировании интереса школьников к урокам физики
Роль домашнего демонстрационного физического эксперимента в формировании интереса школьников к урокам физики Главное дело Архимеда и Картографическая проекция
Главное дело Архимеда и Картографическая проекция Презентация на тему Давление в жидкостях и газах (тесты)
Презентация на тему Давление в жидкостях и газах (тесты)  Физические свойства наноматериалов
Физические свойства наноматериалов Колебания математического и пружинного маятников
Колебания математического и пружинного маятников Волновые явления Механические волны Звуковые волны
Волновые явления Механические волны Звуковые волны Расчёт режимов разомкнутых сетей
Расчёт режимов разомкнутых сетей Описание квантовых ансамблей и процессов релаксации
Описание квантовых ансамблей и процессов релаксации Механические колебания. 9 класс
Механические колебания. 9 класс Лекция16
Лекция16 Уравнения Максвелла
Уравнения Максвелла Автомобильдегі энергияны беру схемасы сіз бұл анықтаманы
Автомобильдегі энергияны беру схемасы сіз бұл анықтаманы Динер Никита Физика Инерция
Динер Никита Физика Инерция От древних источников света до современной лампочки
От древних источников света до современной лампочки Коэффициент отражения
Коэффициент отражения Полупроводник во внешнем электрическом поле
Полупроводник во внешнем электрическом поле Основное уравнение МКТ. Связь кинетичекой энергии с температурой
Основное уравнение МКТ. Связь кинетичекой энергии с температурой Термохалинная структура
Термохалинная структура