Слайд 20Задача 1
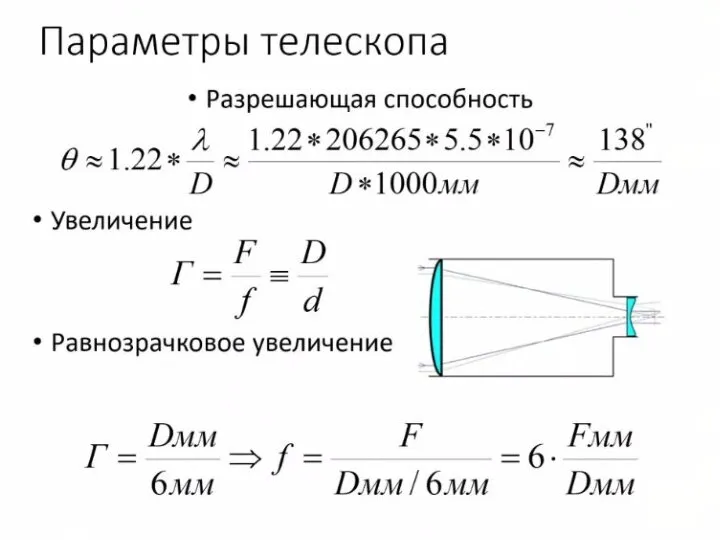
Астроном наблюдает полную Луну в два телескопа с одинаковыми окулярами с

фокусным расстоянием 2.5 см. Объектив первого телескопа имеет диаметр 5 см и фокусное расстояние 1 метр. Второй телескоп имеет объектив диаметром 50 см с фокусным расстоянием 5 метров. Центр диска Луны совпадает с центром поля зрения. Сравните освещенность центральной части глазного дна наблюдателя в обоих случаях.
Слайд 21Построим оптическую схему системы «телескоп – глаз наблюдателя».
Обозначим диаметр объектива через
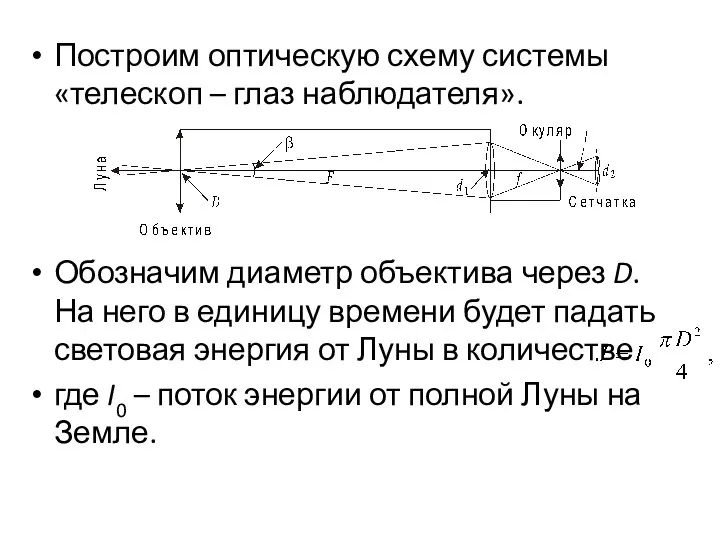
D. На него в единицу времени будет падать световая энергия от Луны в количестве
где I0 – поток энергии от полной Луны на Земле.
Слайд 22Захваченное объективом излучение будет передаваться на фокальную плоскость, в которой получится изображение

диска Луны диаметром d1 = βF,
где β – угловой диаметр Луны, а F – фокусное расстояние объектива.
Освещенность в центре изображения будет равна
Слайд 23Далее свет проходит систему из окуляра с фокусным расстоянием f и глаза

с фокусным расстоянием l. Чтобы весь свет попал в глаз, диаметр выходного пучка d не должен превышать диаметр зрачка глаза, равный 6 мм. Для диаметра выходного пучка справедливо выражение
Для двух рассматриваемых телескопов диаметр выходного пучка получается равным соответственно 1.25 и 2.5 мм, что удовлетворяет указанному условию.
Слайд 24В этом случае на сетчатке формируется еще одно изображение диска Луны с

размером
и освещенностью в центре
Так как речь идет о центре поля зрения, данная величина не зависит от величины поля зрения окуляра. Отношение величин освещенности сетчатки для первого и второго телескопов составит
Освещенность при использовании второго телескопа будет вчетверо больше, чем при использовании первого телескопа.
Слайд 25Задача 2
Световой пучок падает вдоль оптической оси на сферическое зеркало диаметром d

с радиусом кривизны R. Определите расстояние фокуса зеркала от центра кривизны, если d << R.
Слайд 26Рассмотрим луч, идущий вдоль оптической оси на расстоянии h от нее. Этот
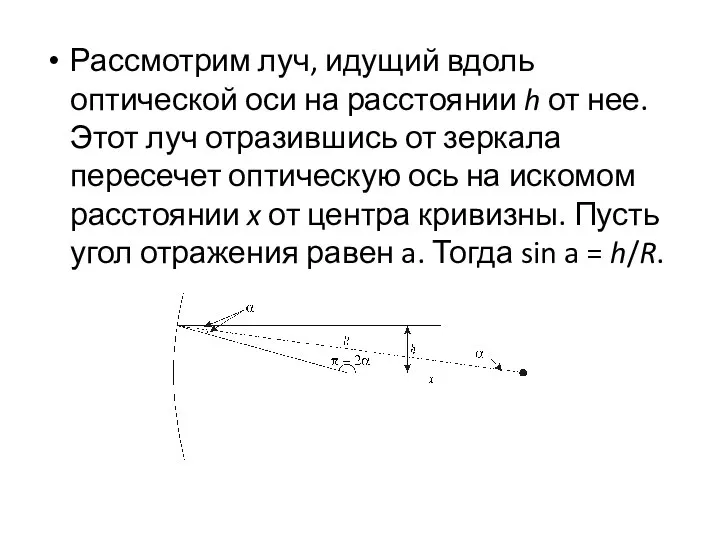
луч отразившись от зеркала пересечет оптическую ось на искомом расстоянии x от центра кривизны. Пусть угол отражения равен a. Тогда sin a = h/R.




















 Урок- лаборатория по физике в 8 классе с применением Дальтон-технологии
Урок- лаборатория по физике в 8 классе с применением Дальтон-технологии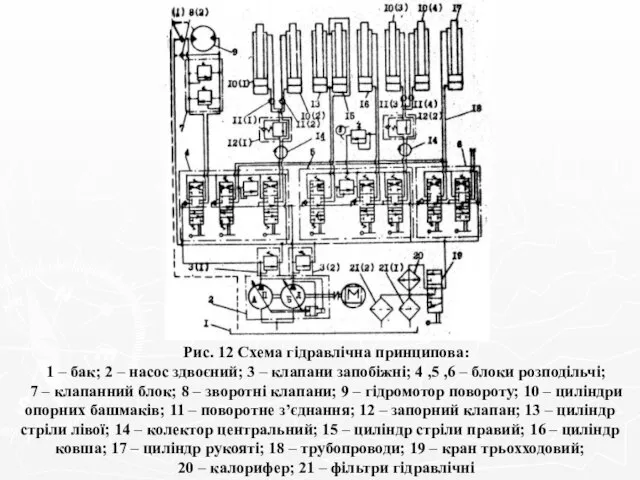 Схема гідравлічна принципова. Билет 7
Схема гідравлічна принципова. Билет 7 Управление физкультурно-спортивными сооружениями
Управление физкультурно-спортивными сооружениями Спектр электромагнитных волн
Спектр электромагнитных волн Последовательное соединение проводников
Последовательное соединение проводников Распределение Максвелла. Распределение Больцмана
Распределение Максвелла. Распределение Больцмана Разработка конструкции микрореакторной установки для получения водорода из водно-спиртовой смесиПрезентация
Разработка конструкции микрореакторной установки для получения водорода из водно-спиртовой смесиПрезентация Линзы. Оптика
Линзы. Оптика Презентация на тему История открытия законов сохранения импульса
Презентация на тему История открытия законов сохранения импульса  Отчёт о проверке автомобиля
Отчёт о проверке автомобиля Определение магнитных сил
Определение магнитных сил Презентация на тему Принцип Гюйгенса. Принцип Ферма. Законы отражения света
Презентация на тему Принцип Гюйгенса. Принцип Ферма. Законы отражения света  Бесконтактный нейтрализатор статических электрических зарядов
Бесконтактный нейтрализатор статических электрических зарядов Виды зубчатых передач
Виды зубчатых передач Радиоактивность в жизни современного человека, значения ядерной энергетики
Радиоактивность в жизни современного человека, значения ядерной энергетики Основные понятия корпускулярной концепции: масса, импульс, сила, кинетическая, потенциальная энергия, работа, мощность
Основные понятия корпускулярной концепции: масса, импульс, сила, кинетическая, потенциальная энергия, работа, мощность Моделирование и экспериментальное исследование разрушения сферической полистироловой микрочастицы в лазерном пучке
Моделирование и экспериментальное исследование разрушения сферической полистироловой микрочастицы в лазерном пучке Графики вокруг нас
Графики вокруг нас Занимательая физика
Занимательая физика Солнечная энергетика
Солнечная энергетика Магнитное поле
Магнитное поле Cилы в механики. 9 класс
Cилы в механики. 9 класс Кипение. Удельная теплота парообразования
Кипение. Удельная теплота парообразования Тепловые двигатели
Тепловые двигатели Механическое движение. Скорость. Единицы скорости
Механическое движение. Скорость. Единицы скорости Динамика. Лекция 2
Динамика. Лекция 2 Растяжение-сжатие прямого бруса
Растяжение-сжатие прямого бруса Обзор способов получения диоксида титана
Обзор способов получения диоксида титана