Лекция 33. Волновая функция

В чём принципиальное отличие
классической физики от квантовой?
Классическая физика опирается на законы, позволяющие точно предсказать движение м.т.*
Она исходит из детерминизма, признающего
строгую закономерность
и причинную обусловленность
всех явлений природы.
*материальная точка
Квантовая физика (физика микрочастиц)
представляет собой возможность
реализации корпускулярных свойств и волновых. Поэтому точно предсказать
траекторию движения невозможно.

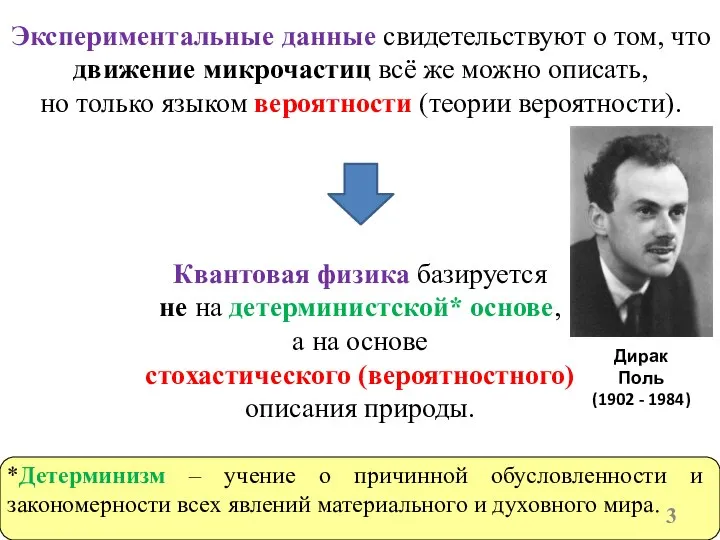
Экспериментальные данные свидетельствуют о том, что движение микрочастиц всё же можно описать,
но только языком вероятности (теории вероятности).
Квантовая физика базируется
не на детерминистской* основе,
а на основе
стохастического (вероятностного)
описания природы.
*Детерминизм – учение о причинной обусловленности и закономерности всех явлений материального и духовного мира.
Дирак Поль
(1902 - 1984)

Как её рассчитать?
Вероятность нахождения частицы в той или иной области можно рассчитать, используя плотность распределения вероятностей (вероятность, отнесённая к единице объёма).
через функцию состояния Ψ (r, t) = Ψ (x, y, z, t)
(пси-функция или волновая функция).
Пси-функция является компле́ксной и
не имеет явного физического смысла!
где Ψ*(r, t) – функция,
компле́ксно сопряжённая по отношению к Ψ(r, t).

КОМПЛЕ́КСНЫЕ ЧИСЛА
Компле́ксное число – это двумерное число.
a+ib – это единое число, а не сложение.
a и b – действительные числа,
i – мнимая единица.
Число a называется действительной частью Rez комплексного числа z,
Число b называется мнимой частью Imz комплексного числа z.

Свойства волновой функции:
Пси-функция должна быть непрерывной, конечной и однозначной во всём рассматриваемом пространстве.
2. Непрерывными должны быть все производные от пси-функции.
3. Пси-функция должна удовлетворять условию нормировки

Вероятность найти частицу в момент времени t в конечном объёме равна
Если квантовая система может находиться в состояниях, описываемых волновыми функциями Ψ1(r, t), Ψ2(r, t), …, Ψn(r, t), то физически допустима и суперпозиция этих состояний, описываемая волновой функцией
c1, c2, …, cn – компле́ксные коэффициенты.
ПРИНЦИП СУПЕРПОЗИЦИИ

Суперпозиция состояний (4) определяется не только модулями комплексных коэффициентов, но и фазами и описывает интерференцию состояний.
Если Ψ1(r, t), Ψ2(r, t), …, Ψn(r, t), характеризуют альтернативные (взаимно исключающие) состояния, то |с1|2, |с2|2, …, |сn|2 являются вероятностями этих состояний. Поскольку сумма всех вероятностей должна быть равна единице, то
Любое среднее значение физической величины y, характеризующее микрообъект, может быть вычислено как

СМЫСЛ ПСИ-ФУНКЦИИ
1. С её помощью можно предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства.
2. Является основным носителем информации о корпускулярных и волновых свойствах частиц.

1926 год. Уравнение Шрёдингера
Шрёдингер Эрвин
(1887 - 1961)
Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике или уравнения Максвелла для электромагнитных волн.
Уравнение Шрёдингера предназначено для
частиц без спина,
движущихся со скоростями много меньшими скорости света.
Уравнение Шрёдингера не выводится, а постулируется методом аналогии с классической оптикой, на основе обобщения экспериментальных данных.

Волновая функция микрочастицы Ψ(r, t) является решением следующего уравнения:
m – масса частицы;
Δ – оператор Лапласа;
i – мнимая единица,
U (x, y, z, t) – потенциальная функция частицы в силовом поле, в котором она движется;
Ψ(x, y, z, t) – волновая функция.
- оператор Лапласа в декартовой системе координат.

Это дифференциальное уравнение (ДУ)
в частных производных.
Вид зависимости потенциальной энергии, граничные и начальные условия определяют вид пси-функции,
что является достаточным условием
для описания движения микрочастиц

Стационарные состояния – состояния с фиксированными значениями энергии.
В этом случае функция U(x, y, z) не зависит явно от времени и имеет вид потенциальной энергии.
Решение уравнения Шредингера (пси-функция) может быть представлено как
E – полная энергия частицы, постоянная в случае стационарного поля.

Подставив (8) в (7), получим
Уравнение Шредингера для стационарных состояний.

Если движение частицы происходит в ограниченной области пространства, то стационарное уравнение Шредингера имеет решения только при определённых дискретных значениях En (энергия имеет дискретный спектр).
Частица, локализованная в конечной области пространства, находится в связанном состоянии. Движение такой частицы называется финитным (ограниченным).
Каждому значению En соответствует своя волновая функция ψn(x,y,z), и знание полного набора этих функций позволяет вычислить все наблюдаемые характеристики микрочастицы.
В тех случаях, когда движение квантовой частицы происходит в неограниченной области пространства, E имеет непрерывный спектр (отсутствует n). Частица в этом случае находится в несвязанном состоянии. Движение частицы в этом случае называется инфинитным (неограниченным).

В этом случае потенциальная энергия U взаимодействия поля с частицей минимальна.
ЧАСТИЦА В ОДНОМЕРНОЙ БЕСКОНЕЧНО ГЛУБОКОЙ ПОТЕНЦИАЛЬНОЙ ЯМЕ
Частица массой m может передвигаться только вдоль какой-либо декартовой оси x.
Потенциальная яма представляет собой интервал от 0 до l (ширина ямы) в пределах которого U(x)=0. В этой области пространства на частицу не действуют силы.

На границах «ямы» потенциальная энергия скачком возрастает до бесконечности.
Запишем уравнение Шредингера в виде
Раз частица не проникает за пределы стенки, то вероятность её обнаружения равна нулю (на границах «ямы» тоже).

Граничные условия будут иметь вид
Внутри «ямы» уравнение Шредингера будет таким:
Общее решение данного ДУ:
С учётом ГУ ψ(0)=0, то B(0)=0.

Следовательно
ψ(l)=Asinkl=0 выполняется только при kl=πn,
n – целые числа.
Энергия En частицы в потенциальной яме с бесконечно высокими стенками принимает лишь определённые дискретные значения, т.е. квантуется.

Введём следующие обозначения:
En – уровни энергии;
n – главное квантовое число. Определяет энергетические уровни частиц.
Подставив в значение , найдем
Постоянную интегрирования A найдём из условия нормировки

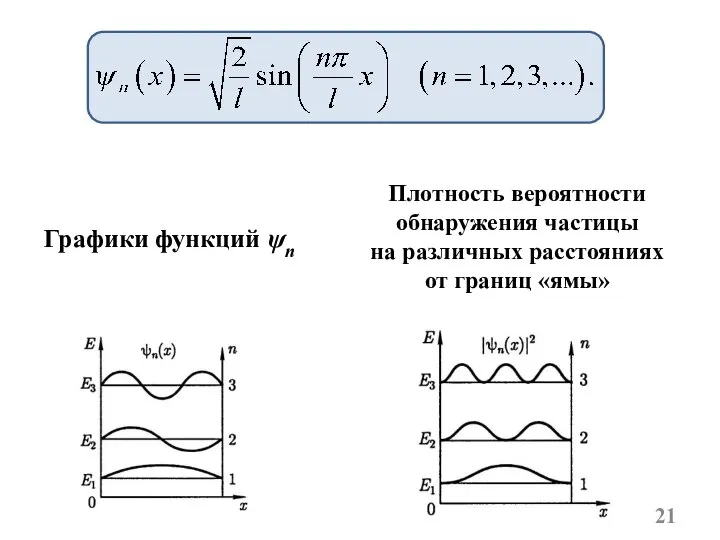
Графики функций ψn
Плотность вероятности
обнаружения частицы
на различных расстояниях
от границ «ямы»

В квантовом состоянии с n=2 частица не может находиться в середине ямы, но одинаково часто может пребывать в её левой и правой частях.
Квантовое состояние с n=0 означает, что частица отсутствует.
Квантовое состояние с n=1 означает, что наиболее вероятное нахождение частицы вблизи центра потенциальной ямы и менее вероятно вблизи краёв.
При n=3 наиболее вероятно обнаружить частицу в центрах каждой третей части потенциальной ямы, и близка к нулю вероятность обнаружения частицы вблизи границ этих частей.

ТУННЕЛЬНЫЙ ЭФФЕКТ.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ СКВОЗЬ ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
Потенциальный барьер конечной ширины – область пространства, в пределах которого потенциальная энергия взаимодействия частицы с внешним полем наибольшая.
Для ПБ прямоугольной формы высотой U и шириной l можем записать

Макрочастица беспрепятственно пройдёт над барьером (при E>U), либо отразится от него (при E
Микрочастица, даже при E>U, имеет отличную от нуля вероятность того, что она отразится от барьера. При E
l, т.е. проникнет сквозь барьер.
Вероятность прохождения частицы через ПБ (коэффициент прозрачности D потенциального барьера) определяется как
D0 – постоянный множитель, который можно приравнять единице;
U – высота потенциального барьера;
E – энергия частицы;
l – ширина барьера.

ИНТЕРПРЕТАЦИЯ ТУННЕЛЬНОГО ЭФФЕКТА
Туннельный эффект – явление чисто квантовое. Оно вытекает из принципа неопределённости Гейзенберга.
Неопределённость координаты x обуславливает неопределённость потенциальной энергии.
Неопределённость проекции импульса px приводит к неопределённости кинетической энергии.
Следовательно, в области потенциального барьера частица не имеет точных значений ни потенциальной, ни кинетической энергий.
Следовательно, существует вероятность того, что значение кинетической энергии частицы превысит ПБ и она сможет его преодолеть.

Переходим от одной частицы к ансамблю частиц
Тождественные частицы – совокупность квантовых частиц, обладающих одинаковыми физическими свойствами.
Состояния системы частиц, отличающиеся перестановкой тождественных частиц местами, нельзя различить ни в каком эксперименте, и такие состояния должны рассматриваться как одно физическое состояние.
Принцип тождественности.

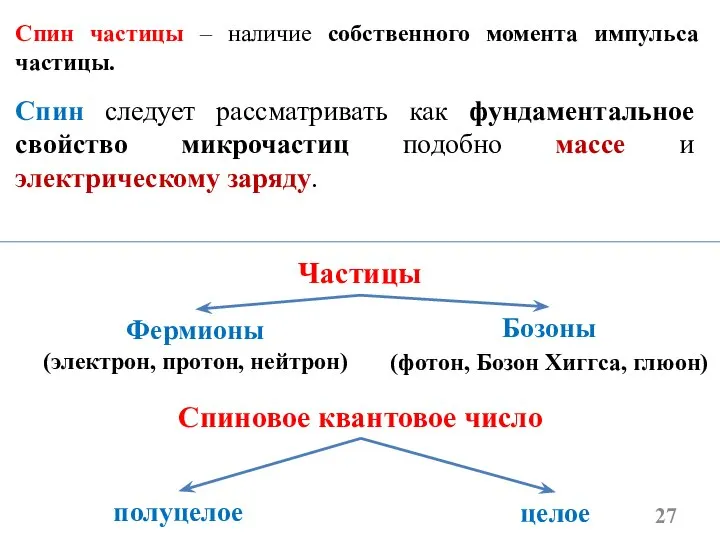
Спин следует рассматривать как фундаментальное свойство микрочастиц подобно массе и электрическому заряду.
Спин частицы – наличие собственного момента импульса частицы.
Частицы
Фермионы
(электрон, протон, нейтрон)
Бозоны
(фотон, Бозон Хиггса, глюон)
Спиновое квантовое число
полуцелое
целое

Сложная частица (например, атомное ядро), составленная из чётного числа фермионов является бозоном, а составленная из нечётного числа фермионов – фермионом.
Принцип Паули. Во взаимодействующей системе фермионов (тождественных частиц) не может быть двух и более частиц, находящихся в одном и том же состоянии.
Одинаковое состояние характеризуется одинаковым набором квантовых чисел –
n (главное),
l (орбитальное),
ml (магнитное),
ms (магнитное спиновое).