Содержание
- 2. Для обеспечения электроэнергией децентрализованных потребителей и использования в качестве резервных источников энергии при авариях всё чаще
- 3. Скорость ветра весьма изменчива, а энергия пропорциональна третьей степени скорости ветра, т.е. при падении скорости ветра
- 4. Поток изменения скорости ветра – это поток случайных событий с интенсивностью уменьшения скорости ветра (отказов) λ0
- 5. Рассмотрим парк ВЭУ, состоящий в общем случае из двух неодинаковых установок, для которых характерны периоды нормальной
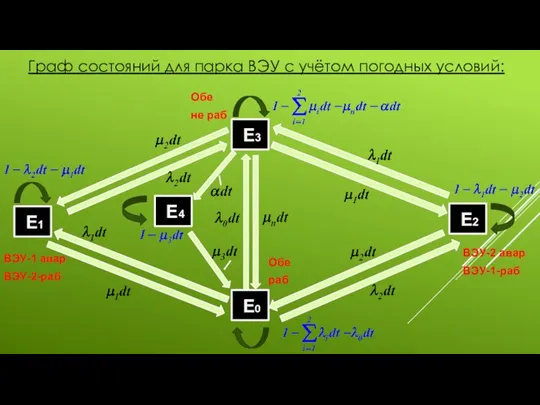
- 6. Состояния ветропарка: Е0 – обе ВЭУ работоспособны; Е1 – ВЭУ-1 в аварийном состоянии, ВЭУ-2 работоспособна; Е2
- 7. λi – интенсивность отказов ВЭУ (i=1,2); μi – интенсивность восстановлений ВЭУ (i=1,2); μ3 – интенсивность одновременного
- 8. Граф состояний для парка ВЭУ с учётом погодных условий: Е0 Е3 Е1 Е2 Е4 Обе не
- 9. Математическая модель представляется системой дифференциальных уравнений первого порядка:
- 10. При начальных условиях (другие вероятности равны нулю) и , решение системы уравнений имеет вид: Где
- 13. Скачать презентацию








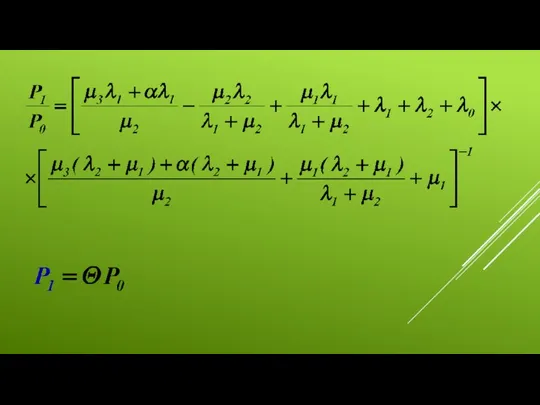
 Произвольная плоская система сил. Лекция 3
Произвольная плоская система сил. Лекция 3 mehanicheskie_kolebaniya
mehanicheskie_kolebaniya Резонанс механических колебаний
Резонанс механических колебаний Давление газа
Давление газа Метод проектов на уроках физики
Метод проектов на уроках физики Электромагнитные явления
Электромагнитные явления Законы электростатики
Законы электростатики Конструкторско-технологическое обеспечение машиностроительных производств профиль технология машиностроения
Конструкторско-технологическое обеспечение машиностроительных производств профиль технология машиностроения Динамика. Масса и сила
Динамика. Масса и сила Основные положения МКТ
Основные положения МКТ Квантовые свойства электромагнитного излучения
Квантовые свойства электромагнитного излучения Атомное ядро. Нуклонная модель ядра. Изотопы. Энергия связи нуклонов в ядре
Атомное ядро. Нуклонная модель ядра. Изотопы. Энергия связи нуклонов в ядре Презентация на тему Конденсаторы
Презентация на тему Конденсаторы  Сила
Сила Чтение чертежей сварных конструкций по системе ЕСКД. на 08.06.2020
Чтение чертежей сварных конструкций по системе ЕСКД. на 08.06.2020 Наглядное пособие для изучения шпоночного и штифтового соединений
Наглядное пособие для изучения шпоночного и штифтового соединений Свободное падение тел
Свободное падение тел Параллельная работа разных трубопроводов
Параллельная работа разных трубопроводов Стабильность градуировочных графиков, их роль в оценке качества количественного химического анализа
Стабильность градуировочных графиков, их роль в оценке качества количественного химического анализа Презентация на тему Путешествие на остров Эврика
Презентация на тему Путешествие на остров Эврика  Задачи на силу Архимеда
Задачи на силу Архимеда Презентация по физике "Физика - это наука понимать природу" -
Презентация по физике "Физика - это наука понимать природу" -  Кривошипно-шатунный механизм
Кривошипно-шатунный механизм Сила трения
Сила трения Уравнение состояния идеального газа. Газовые законы
Уравнение состояния идеального газа. Газовые законы Сила упругости
Сила упругости Презентация на тему Типы интегральных схем
Презентация на тему Типы интегральных схем  Презентация на тему Ядерные реакции
Презентация на тему Ядерные реакции