Содержание
- 2. Введение Цель: изучить и реализовать алгоритм быстрого преобразования Фурье и выяснить, как избежать ошибочного определения фундаментальной
- 3. Преобразование Фурье
- 4. Замена N-точечного ДПФ двумя 0,5N-точечными ДПФ
- 5. БПФ
- 6. Быстрое преобразование Фурье с прореживанием по времени
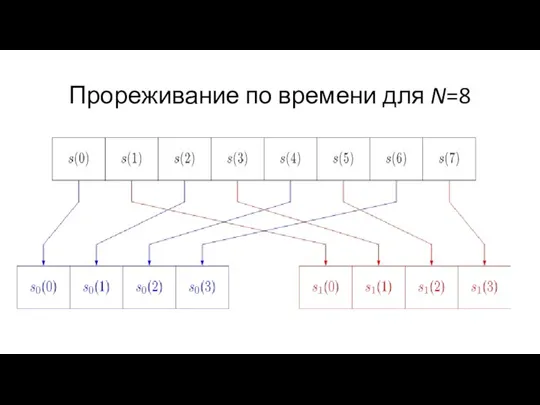
- 7. Прореживание по времени для N=8
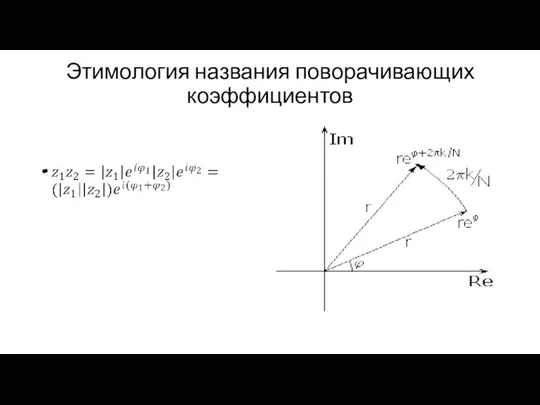
- 10. Этимология названия поворачивающих коэффициентов
- 11. Свойства поворачивающих коэффициентов
- 12. Граф «бабочка»
- 13. Такую процедуру объединения можно применить для расчёта каждого из 0,5N-точечных ДПФ S0(k) и S1(k) через два
- 14. Полный граф алгоритма БПФ по основанию 2 с прореживанием по времени для N=8
- 15. На первом этапе отсчёты входного сигнала переставляются местами, и исходная последовательность делится на «чётную» и «нечётную»
- 16. Основные идеи алгоритма БПФ Разделить сумму (1) из N слагаемых на две суммы по N/2 слагаемых
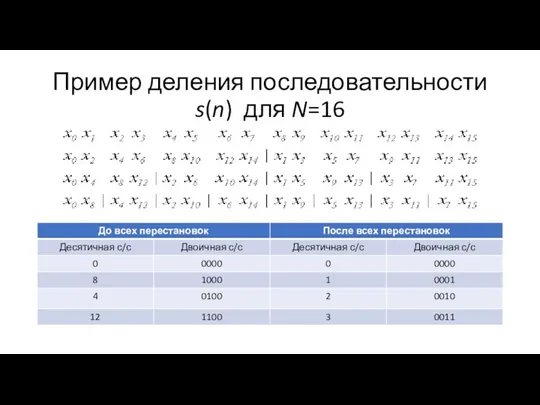
- 17. Пример деления последовательности s(n) для N=16
- 19. Циклический сдвиг вправо Циклический сдвиг вправо при одном разбиении Циклический сдвиг вправо при многократных разбиениях
- 20. Оптимизация вычисления поворачивающих коэффициентов
- 25. Основные задачи психоакустики понять, как слуховая система расшифровывает звуковой образ установить основные соответствия между физическими стимулами
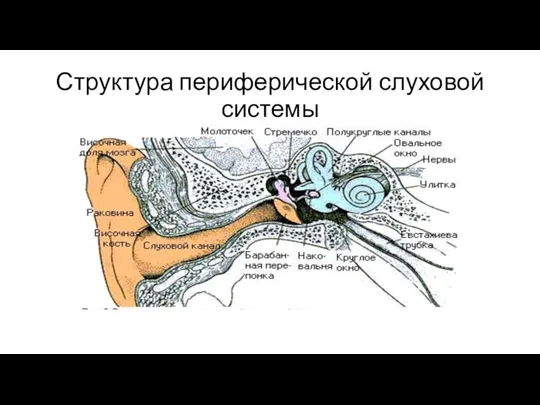
- 26. Периферическая часть слухового анализатора акустическая антенна, принимающая, локализующая, фокусирующая и усиливающая звуковой сигнал; микрофон; частотный и
- 27. Основные функции внешних ушей бинауральное (пространственное) восприятие локализация звукового источника усиление звуковой энергии
- 28. Строение внешних ушей Уши и голова – компоненты внешней акустической антенны Слуховой канал представляет собой изогнутую
- 29. Структура периферической слуховой системы
- 30. Строение среднего уха Это заполненная воздухом полость, соединённая с носоглоткой евстахиевой трубой для выравнивания атмосферного давления.
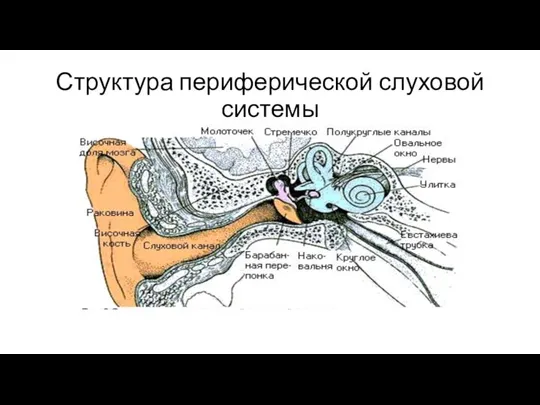
- 31. Структура периферической слуховой системы
- 32. Основные функции среднего уха согласование импеданса воздушной среды с жидкой средой улитки внутреннего уха защита от
- 33. Строение внутреннего уха орган равновесия (вестибулярный аппарат) улитка
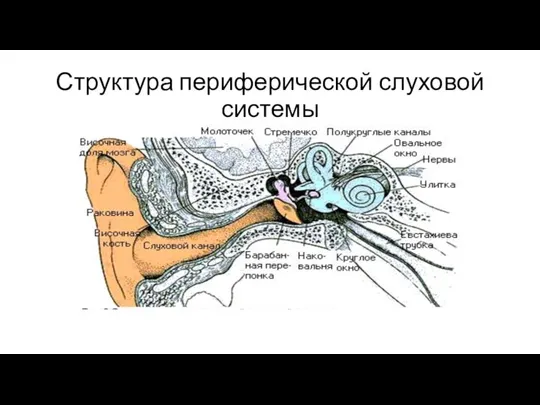
- 34. Структура периферической слуховой системы
- 35. Строение улитки Это трубка переменного сечения, свёрнутая три раза, внутри по всей длине она разделена двумя
- 36. Схематическое изображение развёрнутой улитки (оп – окно преддверия)
- 37. Базилярная мембрана Состоит из нескольких тысяч поперечных волокон: длина – 32 мм, ширина у стремечка –
- 38. Слуховой нерв представляет собой перекрученный ствол, сердцевина которого состоит из волокон, отходящих от верхушки улитки, а
- 39. Упрощённый механизм передачи звука Звуковые волны проходят звуковой канал и возбуждают колебания барабанной перепонки Эти колебания
- 40. Бегущая волна на базилярной мембране
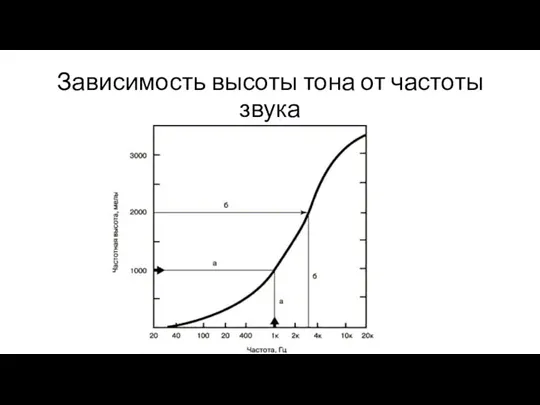
- 42. Зависимость высоты тона от частоты звука
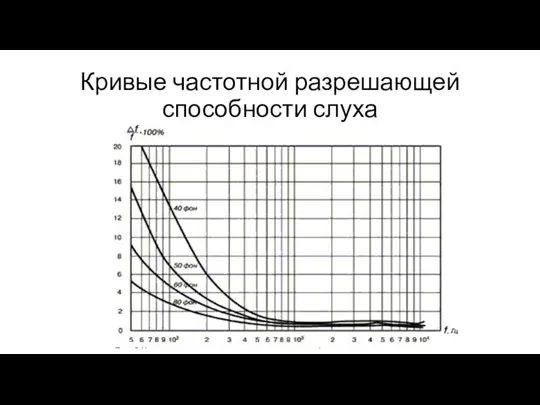
- 43. Кривые частотной разрешающей способности слуха
- 44. Зависимость высоты звука от его интенсивности
- 45. Ощущение высоты тона зависит и от его длительности: короткие звуки воспринимаются как сухой щелчок, но при
- 46. В музыке простые синусоидальные тоны практически не используются, каждый музыкальный тон имеет сложную структуру и состоит
- 47. До частоты примерно 5000 Гц увеличение высоты тона на октаву связано с удвоением частоты. Но выше
- 48. Теория места Теория места при восприятии высоты основана на способности базилярной мембраны выполнять частотный анализ сложного
- 49. В зависимости от спектрального состава на базилярной мембране возбуждаются различные участки. Возбуждаются волосковые клетки, находящиеся на
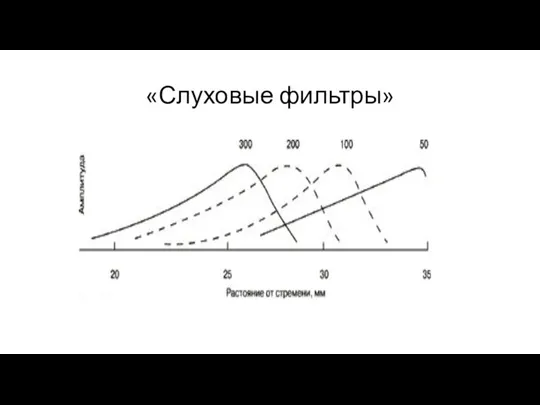
- 50. При действии синусоидального сигнала в слуховом нерве формируется «образец возбуждения» – скорость разрядов нейронов как функция
- 51. «Слуховые фильтры»
- 52. Методы определения высоты
- 53. Метод 1 Присутствие фундаментальной частоты является обязательным для определения высоты звука Но в 1940 году Шутен
- 54. Метод 2 Для большинства музыкальных звуков соседние гармоники обычно присутствуют. Слуховая система, оценивая положение их максимумов
- 55. Метод 3 Позволяет объяснить и пропущенную фундаментальную частоту, и наличие только нечётных гармоник, т.к. от отсутствия
- 56. Выводы теории места Механизм места разворачивает данную гармонику, если критическая полоса её слухового фильтра, построенного на
- 57. Выводы теории места Теория места создаёт базис для понимания того, как можно определить высоту путём анализа
- 58. Временная теория Эта теория использует синхронизацию разрядов нейронов органа Корти с фазой колебания базилярной мембраны (эффект
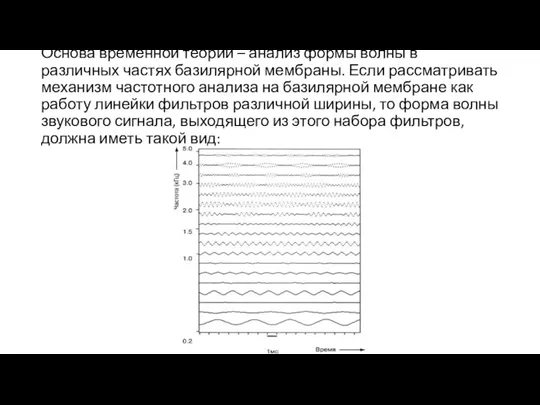
- 59. Основа временной теории – анализ формы волны в различных частях базилярной мембраны. Если рассматривать механизм частотного
- 60. Волновая форма выходного сигнала для фильтра, центральная частота которого выше шестой, не синусоидальная, т.к. гармоники не
- 61. Минимальное время между импульсами от различных мест на базилярной мембране определяется периодом волны, выходящей от соответствующего
- 62. Основа временной теории восприятия высоты тона Мозг определяет периодичность разрядов и по ним восстанавливает частоту основного
- 63. Выводы временной теории Временная теория позволяет понять, как найти фундаментальную частоту на основе анализа временных интервалов
- 64. Современная теория восприятия высоты тона Согласно современным теориям, мозг принимает информацию от периферийной слуховой системы как
- 65. Современная модель для восприятия высоты тона
- 66. Анализ восприятия высоты музыкального тона с помощью предложенной модели позволил получить ряд интересных результатов: Для музыкальных
- 67. Музыкальные звуки, содержащие только неразвёрнутые гармоники (свыше шестой), могут дать ощущение высоты тона по огибающей, при
- 68. Обработка звуковой информации в мозге В настоящее время принята гипотеза, что мозг, получив информацию от периферической
- 69. Применение теории восприятия высоты тона к программе В программе был применён 1 метод теории места, в
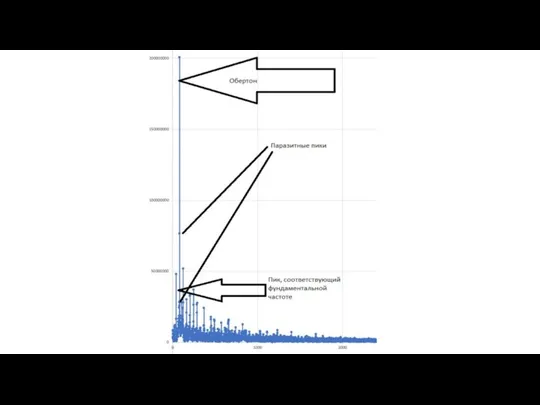
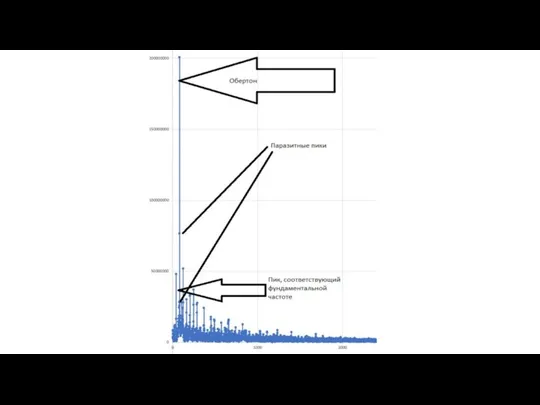
- 70. Возникшие проблемы Но возникла проблема: в амплитудном спектре пик с максимальной среди всех других амплитудой оказался
- 72. Заключение В ходе данной работы был изучен и реализован алгоритм быстрого преобразования Фурье по основанию два
- 74. Скачать презентацию



























































 Антуан Анри Беккерель
Антуан Анри Беккерель Закон сохранения импульса
Закон сохранения импульса Электрооборудование автомобиля, стартер, генератор Автомобиля ВАЗ-2190
Электрооборудование автомобиля, стартер, генератор Автомобиля ВАЗ-2190 Задание по физике в формате ОГЭ
Задание по физике в формате ОГЭ Решение задач. Силы тяжести, упругости
Решение задач. Силы тяжести, упругости Методы подобия физических процессов
Методы подобия физических процессов Закон Архимеда
Закон Архимеда Сообщающиеся сосуды (урок физики, 7 класс)
Сообщающиеся сосуды (урок физики, 7 класс) Средства автоматизации измерения, контроля и управления. Лекция 8
Средства автоматизации измерения, контроля и управления. Лекция 8 Накопление механической энергии
Накопление механической энергии Явление электромагнитной индукции
Явление электромагнитной индукции Технологии обработки материалов. Лекция 14
Технологии обработки материалов. Лекция 14 Трансмиссия автомобиля
Трансмиссия автомобиля Работа в термодинамике
Работа в термодинамике Движение в физике. Звук
Движение в физике. Звук Механические колебания
Механические колебания Повторялка
Повторялка Автор: Тараканова Светлана школа № 14, 8 А класс
Автор: Тараканова Светлана школа № 14, 8 А класс Физика в загадках. Своя игра
Физика в загадках. Своя игра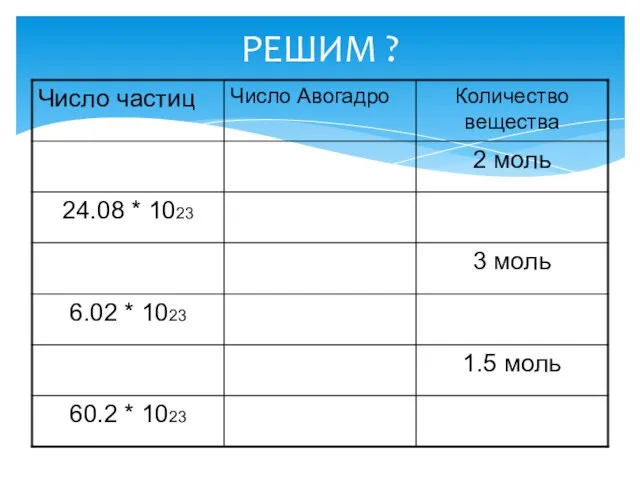 Молярный объем газообразных веществ
Молярный объем газообразных веществ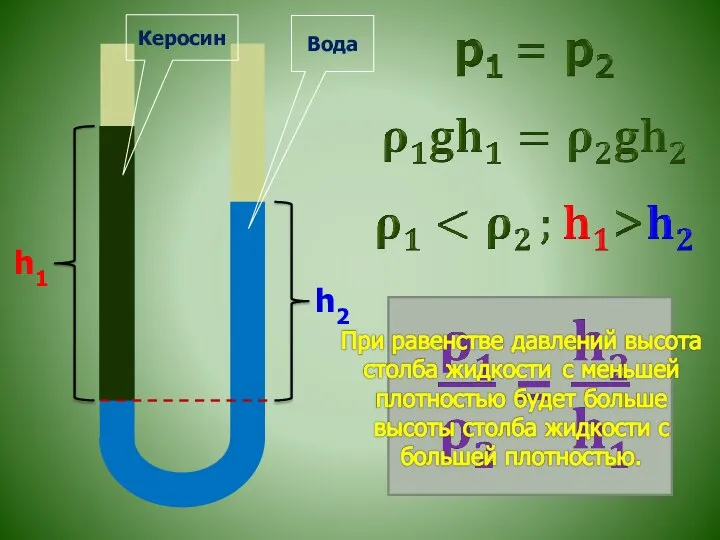 Шлюзы и фонтаны
Шлюзы и фонтаны Идентификация и моделирование CW–crds спектра поглощения молекулы двуокиси азота в области 6000 – 6400 см -1
Идентификация и моделирование CW–crds спектра поглощения молекулы двуокиси азота в области 6000 – 6400 см -1 konspekt (1)
konspekt (1) Вычислительные методы механики деформируемого тела
Вычислительные методы механики деформируемого тела Виды весов
Виды весов Лазеры. Использование приемов ЛСМ как способа достижения метапредметных образовательных результатов
Лазеры. Использование приемов ЛСМ как способа достижения метапредметных образовательных результатов Апоптоз: молекулярные причины и значения
Апоптоз: молекулярные причины и значения Постоянный электрический ток
Постоянный электрический ток