Молекулярная физика. Лекция 10

Молекулярная физика
Используя соотношения и , получим:
и . Полученную формулу называют формулой Больцмана. Для давления будем иметь
, где и при Eпот=0.
В поле силы тяжести вблизи поверхности Земли
,
где m0 – масса молекулы газа, M – его молярная
масса. Последнюю формулу называют барометри-
ческой. Зависимость давления от высоты z над
поверхностью земли при разных температурах и молярных массах представлена на рисунке.

Молекулярная физика
Распределение молекул по скоростям. Распределение Максвелла.
В связи с тем, что в макроскопических объемах газа содержится ас-трономическое число молекул, бессмысленно говорить об опреде-лении точного значения скорости каждой из них. С одной стороны, это сложно осуществить технически, а с другой стороны, молекулы, постоянно сталкиваясь, меняют величину и направление скорости. При таком большом количестве частиц можно говорить лишь о вероятности того, что определенная часть молекул имеет скорости лежащие в некотором интервале от до . Решением подобных задач занимается статистическая физика.
Введем понятие вероятности. Вероятностью называется относитель-ная частота выпадения того или иного события. Игральная кость при падении оказывается одной гранью вверх. Вероятность выпа-дения, например, числа 3 равна числу выпадения тройки, отнесен-ному к общему числу бросаний

Молекулярная физика
Сумма выпадения всех возможных 6 чисел равна .
Пусть из общего числа молекул N скорости, лежащие в интервале от v до v + dv имеют dN молекул. Вероятность dP того, что молекулы имеют скорости, лежащие в этих пределах пропорцио-нальна , т.е. равна , где вероятность выражена через величину интервала скоростей , а функция называется функцией распределения молекул по скоростям.
Будем искать , используя формулу Больцмана. Для этого рассмотрим идеальный газ в состоянии теплового равновесия в однородном гравитационном поле и будем следить только за z компонентой скоростей его молекул. Пусть число молекул в единице объема со скоростями, лежащими в интервале от
до равно . Рассмотрим бесконечно тонкий слой газа площадью S толщиной dz на высоте z. В его объеме содержится молекул, где n(z) -

Молекулярная физика
плотность газа на высоте z. Через некоторое время молекулы этого слоя при тепловом движении сместится на другую высоту z’ и изменит свою толщину от до , а скорости под действием сил поля изменятся и перейдут в интервал от до . Число молекул в этом объеме можно представить в виде .
Поскольку число молекул осталось неизменным, то
.
В поле силы тяжести горизонтальные составляющие скорости не меняются, и закон сохранения энергии примет вид:
Дифференцируя при постоянных z и z’, получим:
, .
Откуда и .

Молекулярная физика
Используя формулу Больцмана, получим:
Из закона сохранения энергии следует:
.
Тогда и .
В результате получено равновесное распределение молекул по значениям только одной компоненты скорости . Доля молекул, обладающих тремя определенными значениями скорости получается перемножением долей
молекул, обладающих каждой из компонент в отдельности.

Молекулярная физика
Таким образом, число молекул dN со скоростями, лежащими в интервалах от до , от до и от до равно
.
если перейти к сферическим координатам и проинтегрировать по
, то .
Константа определяется из соотношения ,
Означающего очевидное утверждение, что молекула имеет какую-то скорость в интервале от 0 до бесконечности. Это событие является достоверным, поэтому его вероятность равна 1.
Функция распределения равна

Молекулярная физика
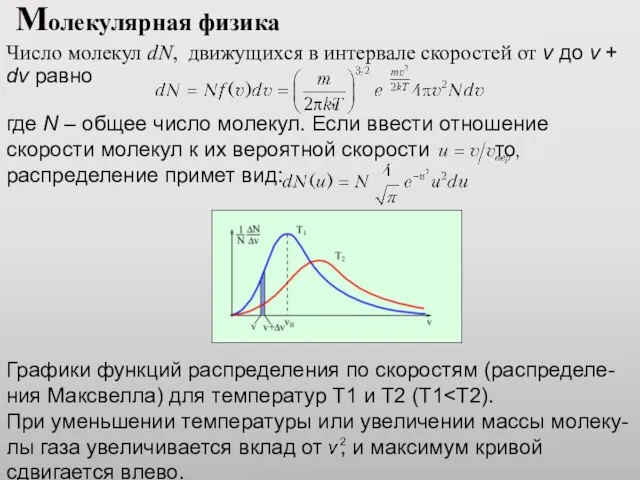
Число молекул dN, движущихся в интервале скоростей от v до v + dv равно
,
где N – общее число молекул. Если ввести отношение скорости молекул к их вероятной скорости то распределение примет вид:
Графики функций распределения по скоростям (распределе-ния Максвелла) для температур Т1 и Т2 (Т1<Т2).
При уменьшении температуры или увеличении массы молеку-лы газа увеличивается вклад от , и максимум кривой сдвигается влево.

Молекулярная физика
1.Наиболее вероятная скорость соответствует максимуму кривой
распределения Максвелла.
,
, где - масса молекулы, M – молярная масса.
2.Средняя скорость молекул .
3.Среднеквадратичная скорость молекул
Пример. Средняя скорость движения молекул
кислорода.
м/с
Распределение молекул по скоростям
Экспериментальное подтверждение распределе-
ния Максвелла получено в опытах Штерна и
Ламмерта.

Молекулярная физика
Примеры решения задач
Задача 62. Найдите суммарную кинетическую энергию вращательного движения молекул углекислого газа (с жесткими связями) массой 88 г при температуре 300 К, молярная масса углекислого газа .
Решение. Молекула углекислого газа CO2 является треха-томной с 6 степенями свободы, три из которых приходятся на вращательное движение. Суммарная кинетическая энергия вращательного движения молекул 88 г (двух молей) CO2 равна
7479 Дж.
Задача 63. При какой температуре Т средняя квадратичная скорость молекул азота больше их наиболее вероятной скорости на
м/с?
Решение. Вычитая из выражения для средней квадратичной скорости наиболее вероятную скорость, получим:

Молекулярная физика
откуда
Задача 64. Найти скорость при которой пересекаются кривые распределения Максвелла молекул по скоростям при температурах Т и 2Т, если наиболее вероятная скорость при температуре 2Т равна.
Решение. В точке пересечения (рис.5) функций распределения (плотностей вероятности) они равны:
,
откуда и
Задача 65. Какая часть молекул кислорода при t = 0°С обладает скоростями от 100 до 110 м/с?
Решение. Запишем распределение Максвелла молекул по
скоростям в виде , где -
относительная скорость, , . Тогда

Молекулярная физика
Задача 66. Найдите разность давлений в салоне самолета, летящего на высоте = 8300 м и за бортом. В салоне поддерживается давление воздуха, соответствующее высоте
=2700 м. Ускорение свободного падения и температура 0°С наружного воздуха от высоты не зависят. Давление на поверхности Земли = 100 кПа, молярная масса воздуха M = 29кг/м3.
Решение. Зависимость давления от высоты над поверхностью Земли дается распределением Больцмана . Тогда давление в салоне равно кПа, а за бортом
кПа. Разность давлений составляет 36 кПа.
Задача 67. Вблизи поверхности Земли отношение объемных концентраций кислорода и азота в воздухе Считая ускорение свободного падения не зависящим от высоты, а темпера-туру атмосферы постоянной и равной 0°С, определить это отношение на высоте h = 10 км.
,