Направление и пределы самопроизвольного протекания физико-химических процессов

Направление и пределы самопроизвольного протекания физико-химических процессов
Самопроизвольные и несамопроизвольные процессы
Энтропия
Второй закон термодинамики
Энергия Гиббса
Энергия Гельмгольца
Химическое сродство

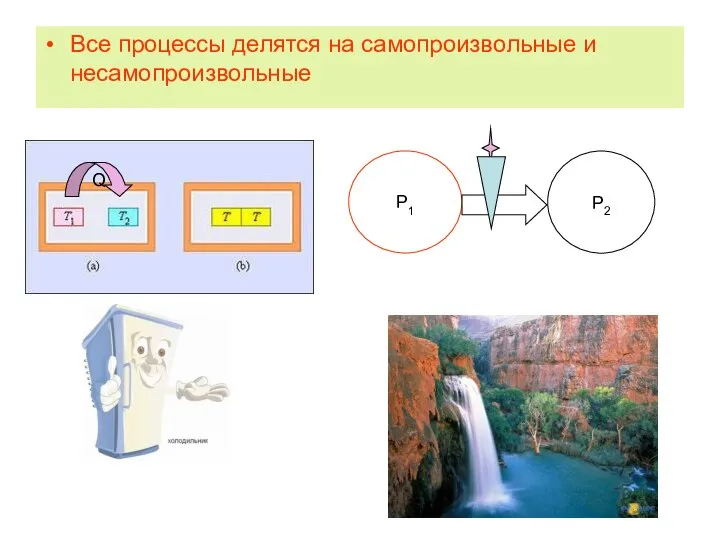
Все процессы делятся на самопроизвольные и несамопроизвольные

Направление и пределы самопроизвольного протекания физико-химических процессов

Особенности самопроизвольных процессов
Протекают без затраты энергии извне
Неравновесные
Необратимые
Если в прямом направлении процесс протекает как самопроизвольный, то в обратном направлении как самопроизвольный не идет
При осуществлении самопроизвольного процесса система способна совершать работу

Критерии направления и пределов протекания самопроизвольного процесса

Метод потенциалов
Самопроизвольное протекание процессов возможно только в направлении выравнивания фактора интенсивности.
Наличие градиента фактора интенсивности предполагает, что этот метод применим только для неоднородных систем

Второй закон термодинамики

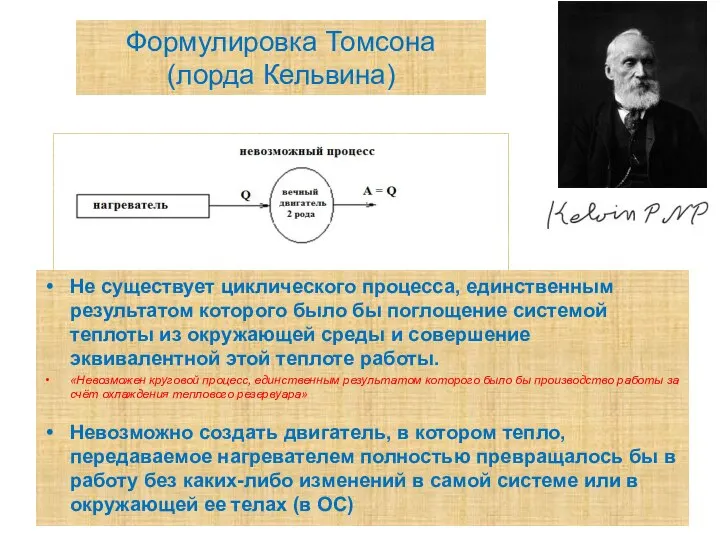
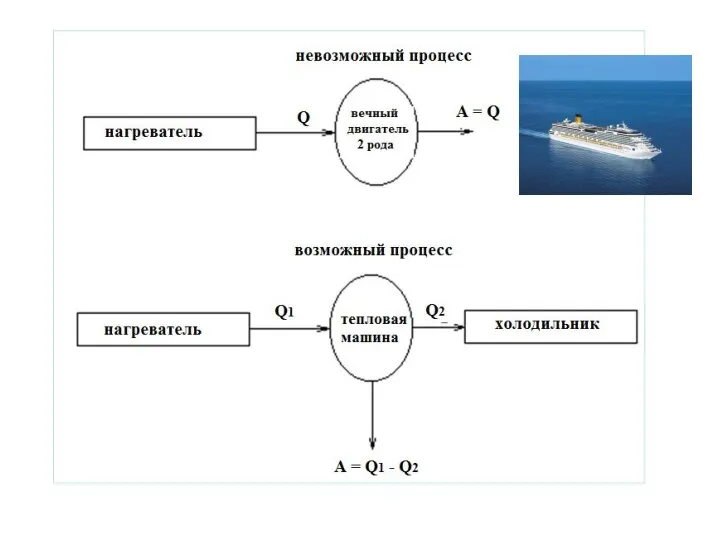
Формулировка Томсона (лорда Кельвина)
Не существует циклического процесса, единственным результатом которого было бы поглощение системой теплоты из окружающей среды и совершение эквивалентной этой теплоте работы.
«Невозможен круговой процесс, единственным результатом которого было бы производство работы за счёт охлаждения теплового резервуара»
Невозможно создать двигатель, в котором тепло, передаваемое нагревателем полностью превращалось бы в работу без каких-либо изменений в самой системе или в окружающей ее телах (в ОС)

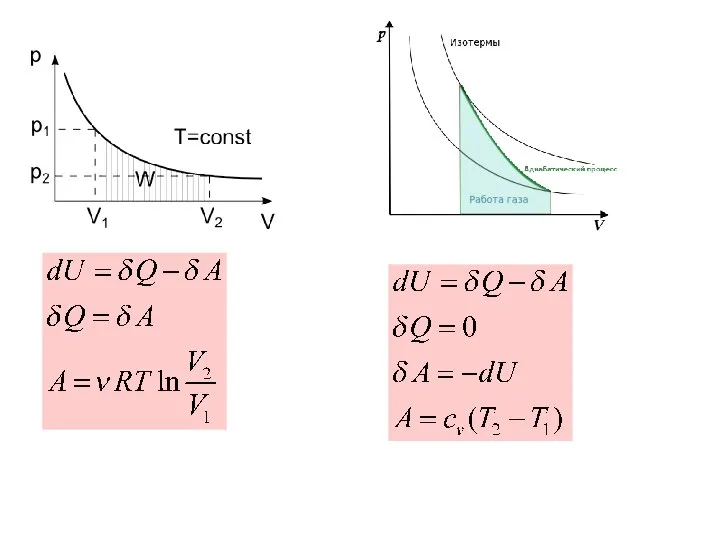
Убедимся в этом!!!
Такое утверждение равносильно утверждению о невозможности процесса превращения теплоты в работу, если в итоге этого процесса состояние рабочего тела остается тем же, каким было в начале процесса и при этом никакие другие части системы не испытали изменений

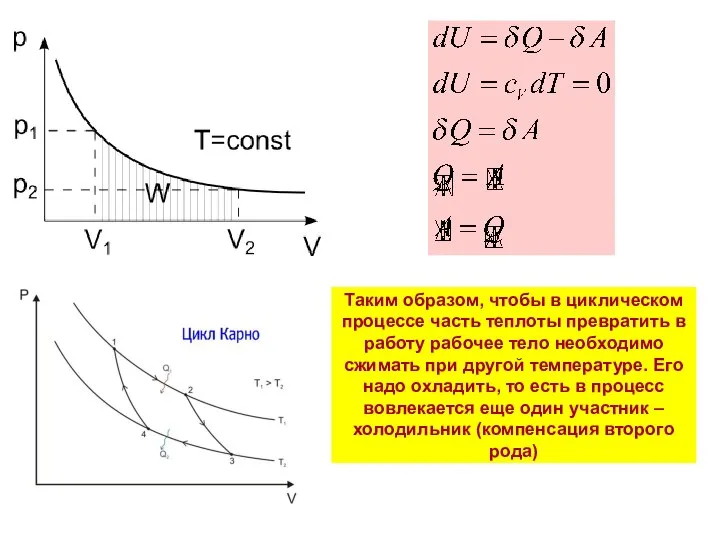
Таким образом, чтобы в циклическом процессе часть теплоты превратить в работу рабочее тело необходимо сжимать при другой температуре. Его надо охладить, то есть в процесс вовлекается еще один участник – холодильник (компенсация второго рода)

Второй закон термодинамики утверждает, что при преобразовании теплоты в работу (неупорядоченных форм движения материи в упорядоченные) наряду с охлаждением теплового источника непременно должны происходить изменения термодинамического состояния еще одного или нескольких тел
Такие изменения получили название компенсаций превращения теплоты в работу:
Компенсации первого рода: изменение термодинамического состояния рабочего тела (невозможны в круговых процессах)
Компенсации второго рода: изменение термодинамического состояния других тел
Таким образом, при самопроизвольном процессе неизменно и однозначно должно что то меняться

Поскольку, согласно закону сохранения энергии, общая энергия системы (мяч – поверхность) не меняется, это означает, что часть энергии мяча перераспределяется, превращается в тепловую энергию движения атомов, образующих поверхность.
Происходит диссипация (рассеяние) энергии направленного движения мяча в тепловое, хаотическое движение частиц.
В то же время трудно предположить, что лежащий на поверхности мяч самопроизвольно подпрыгнет. Для этого необходимо, чтобы мяч получил направленный импульс от частиц, образующих поверхность. Для этого необходимо, чтобы произошел самопроизвольный процесс превращения хаотического, теплового, движения частиц в упорядоченное движение.
Таким образом, самопроизвольно протекают переходы от более упорядоченных к менее упорядоченным формам движения.
Формулировка второго закона термодинамики, данная Кельвиным, является обобщением опыта «прыгающий мяч»

Еще примеры
Газ не может самопроизвольно сжаться, так как для этого необходимо, чтобы все частицы получили возможность собраться в одной части сосуда, получили возможность коллективного направленного движения. В то же время, расширение газа –самопроизвольный процесс.
Температура тела не может стать больше температуры окружающей среды, с которой оно находится в состоянии теплового равновесия. Маловероятно, чтобы столкновения с хаотически движущимися частицами ОС создали условия для приобретения телом дополнительной энергии

Некоторые промежуточные выводы
Когда протекают самопроизвольные процессы, несмотря на то, что полная энергия изолированной системы остается постоянной, в процессе происходит ее перераспределение. Таким образом, логично считать, что направление самопроизвольного процесса должно быть связано с перераспределением энергии.
При протекании самопроизвольного процесса происходит рассеяние (диссипация энергии), которая приводит систему в менее упорядоченное состояние.
Для определения направления самопроизвольно протекающего процесса необходимо найти такое его направление, в ходе которого будет происходить максимальное рассеяние общей энергии изолированной (ТС+ОС) системы.
Принимая во внимание, что существуют две формы передачи энергии: работа (упорядоченная форма) и теплота (неупорядоченная форма), критерии направленности самопроизвольных процессов следует искать в процессах превращения теплоты в работу или работы в теплоту.
В своем развитии системы стремятся к беспорядку.

Логическая природа второго закона термодинамики
Выбрать процесс, для которого многовековой опыт позволяет четко указать, какое направление является самопроизвольным.
Постулировать этот опыт.
Опираясь на постулат найти и доказать, что существует некоторое свойство в системе (функция состояния), знак изменения которого позволяет однозначно определить направление самопроизвольного процесса
Постулат Клаузиуса: «Невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому»
«Теплота не может переходить от холодного тела к теплому сама собой (самопроизвольно) даровым процессом»

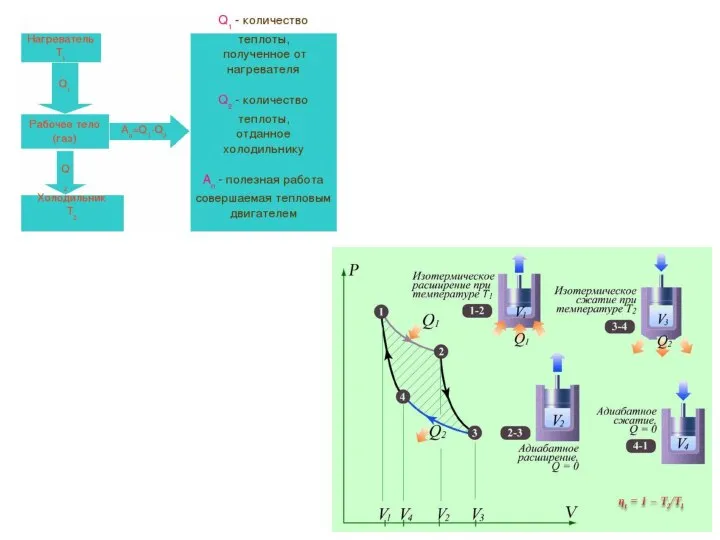
Рассмотрим переход тепла от более нагретого тела (нагревателя) к менее нагретому (холодильнику) посредством рабочего тела тепловой машины:
В равновесном процессе
В неравновесном (самопроизвольном процессе)

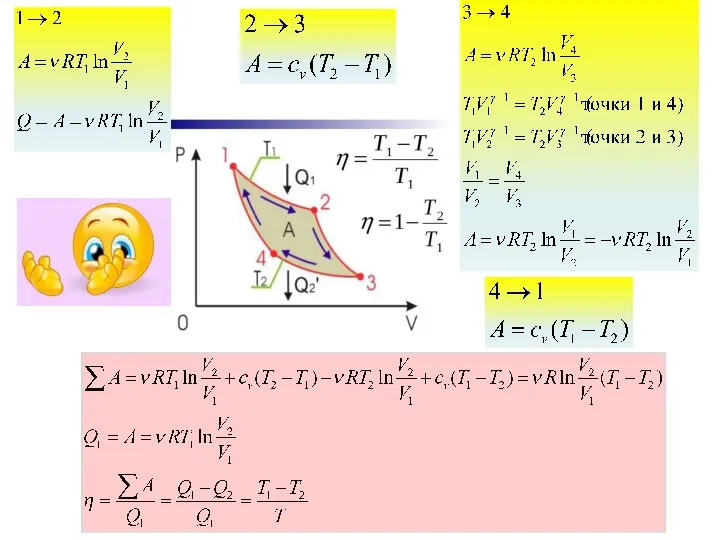
Теорема Карно

«Движущая сила тепла не зависит от агентов, взятых для её развития; её количество исключительно определяется температурами тел, между которыми, в конечном счете, производится перенос теплорода» (Сади Карно)
КПД цикла Карно не зависит от природы рабочего тела и конструкции теплового двигателя и является функцией температур нагревателя и холодильника

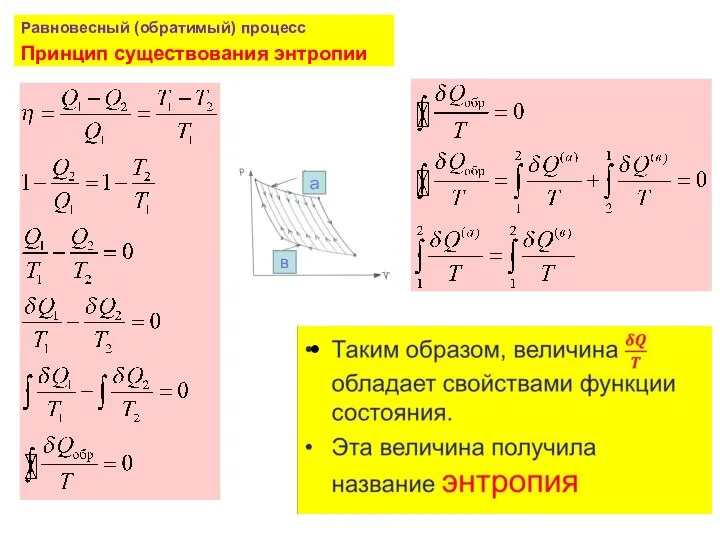
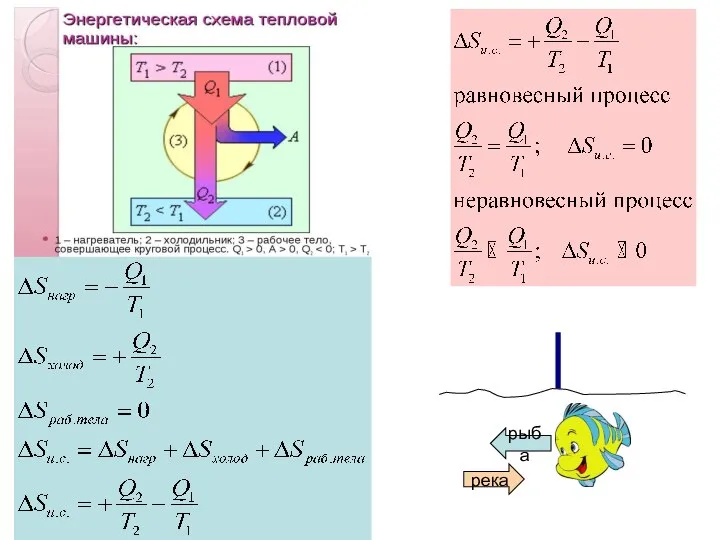
Равновесный (обратимый) процесс
Принцип существования энтропии

Неравновесный (необратимый) процесс
принцип возрастания энтропии
Таким образом:
если процесс является неравновесным и необратимым (самопроизвольным), то количество приведенной теплоты, которое необходимо отдать рабочему телу машины холодильнику, чтобы вернуться в исходное состояние после циклического процесса больше, чем в равновесном процессе.
В неравновесном процессе энтропия изолированной системы возрастает (генерируется в результате неравновесности дополнительное количество энтропии

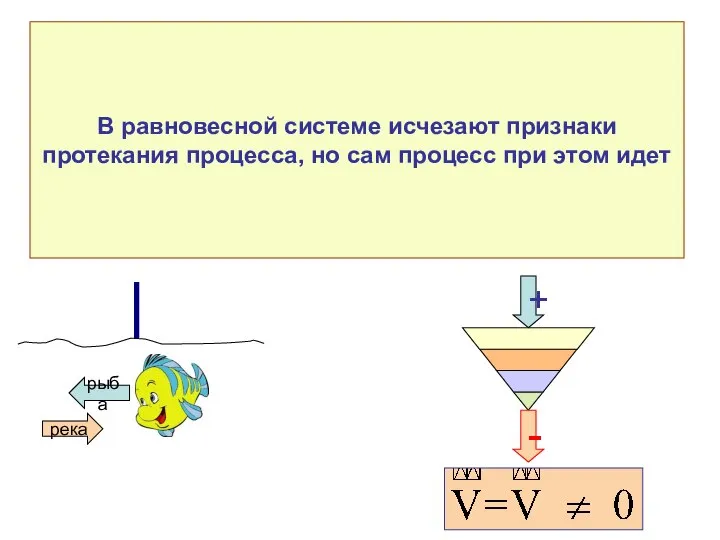
В равновесной системе исчезают признаки протекания процесса, но сам процесс при этом идет

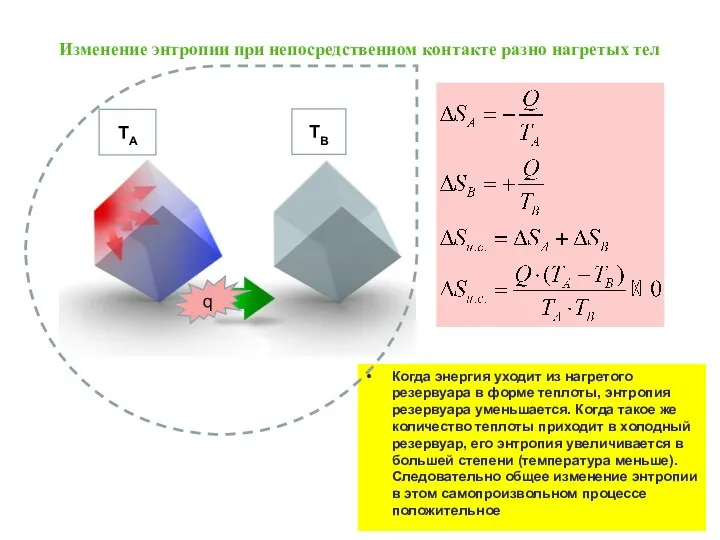
Обратим внимание, что передача эквивалентного количества тепла при разных температурах приводит к разному изменению энтропии. Чем температура ниже, тем рост энтропии (беспорядка) в системе больше.
Термодинамическое определение энтропии:
приведенная теплота

Изменение энтропии при непосредственном контакте разно нагретых тел
Когда энергия уходит из нагретого резервуара в форме теплоты, энтропия резервуара уменьшается. Когда такое же количество теплоты приходит в холодный резервуар, его энтропия увеличивается в большей степени (температура меньше). Следовательно общее изменение энтропии в этом самопроизвольном процессе положительное

Любой циклический процесс может быть представлен бесконечно большим числом бесконечно малых циклов Карно. Поэтому полученные соотношения и выводы могут быть распространены на любой циклический процесс

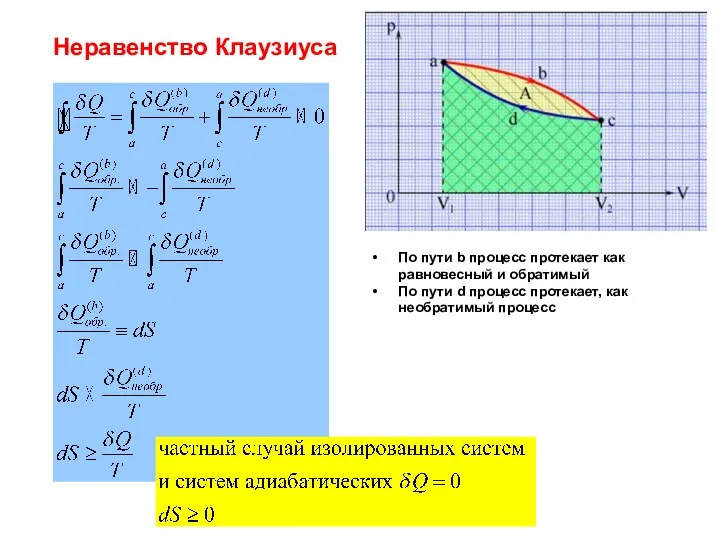
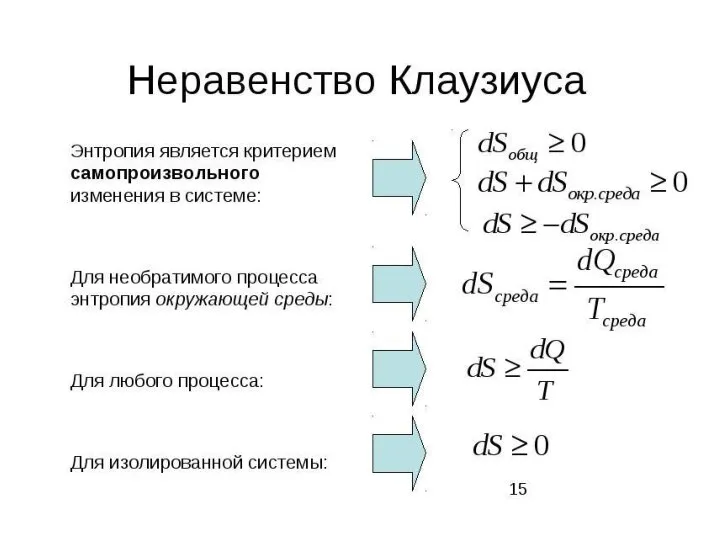
Неравенство Клаузиуса
По пути b процесс протекает как равновесный и обратимый
По пути d процесс протекает, как необратимый процесс

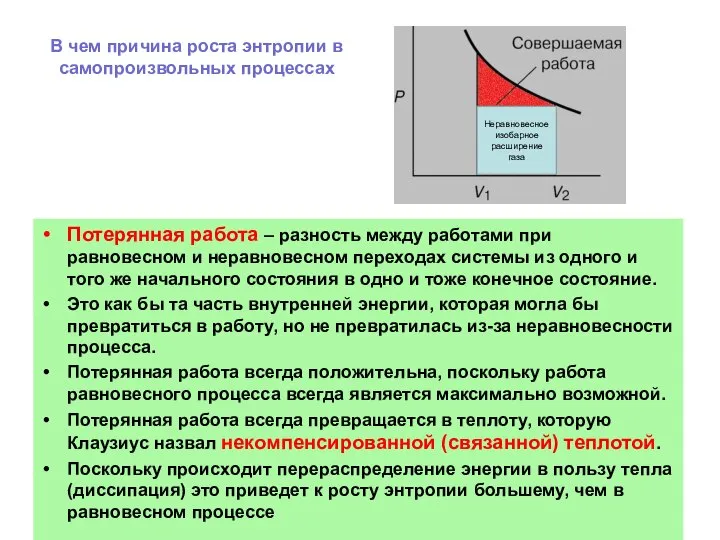
В чем причина роста энтропии в самопроизвольных процессах
Потерянная работа – разность между работами при равновесном и неравновесном переходах системы из одного и того же начального состояния в одно и тоже конечное состояние.
Это как бы та часть внутренней энергии, которая могла бы превратиться в работу, но не превратилась из-за неравновесности процесса.
Потерянная работа всегда положительна, поскольку работа равновесного процесса всегда является максимально возможной.
Потерянная работа всегда превращается в теплоту, которую Клаузиус назвал некомпенсированной (связанной) теплотой.
Поскольку происходит перераспределение энергии в пользу тепла (диссипация) это приведет к росту энтропии большему, чем в равновесном процессе
Неравновесное
изобарное расширение
газа

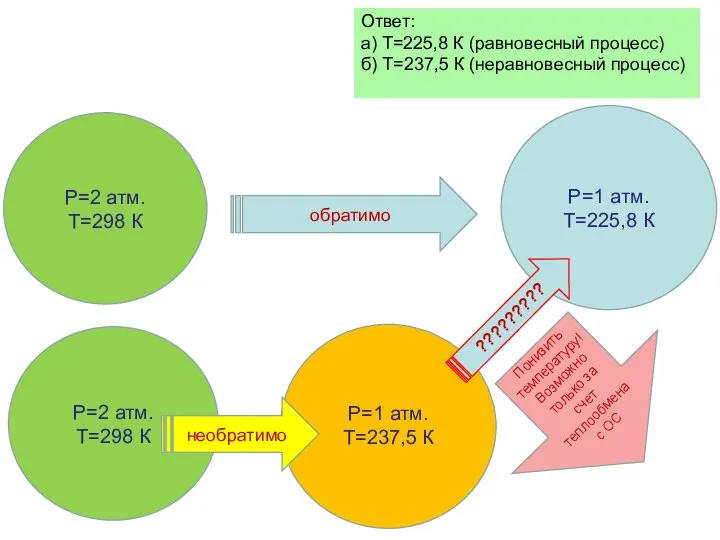
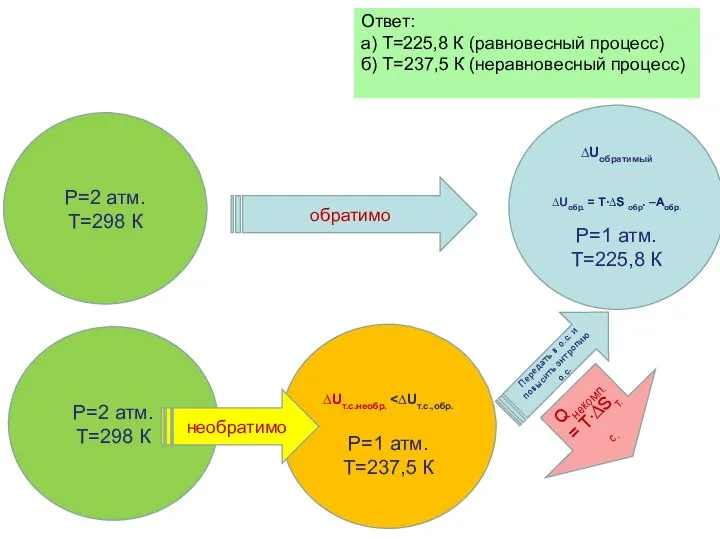
Задача
Один моль Хе, находящийся при температуре 250 С и давлении 2 атмосферы расширяется адиабатически:
а) обратимо до 1 атмосферы
б) против давления 1 атмосфера
Какой будет конечная температура в каждом случае?

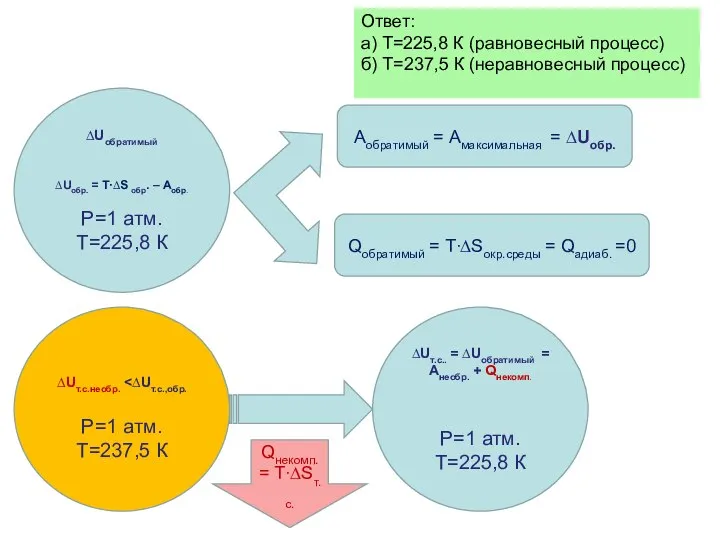
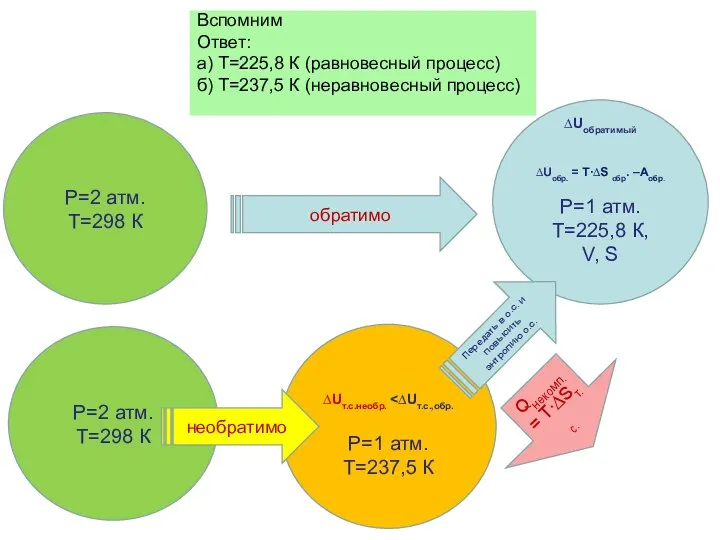
Ответ:
а) Т=225,8 К (равновесный процесс)
б) Т=237,5 К (неравновесный процесс)
Р=1 атм.
Т=225,8 К
Р=1 атм.
Т=237,5 К
?????????
Понизить температуру! Возможно только за счет теплообмена с ОС
Р=2 атм.
Т=298 К
Р=2 атм.
Т=298 К
обратимо
необратимо

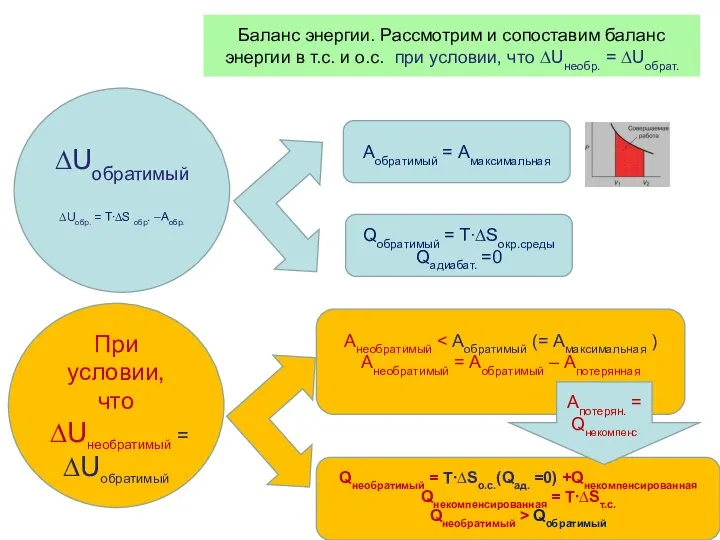
Баланс энергии. Рассмотрим и сопоставим баланс энергии в т.с. и о.с. при условии, что ∆Uнеобр. = ∆Uобрат.
∆Uобратимый
∆Uобр. = T∙∆S обр. –Аобр.
При условии, что
∆Uнеобратимый =
∆Uобратимый
Аобратимый = Амаксимальная
Анеобратимый < Аобратимый (= Амаксимальная )
Анеобратимый = Аобратимый – Апотерянная
Qобратимый = T∙∆Sокр.среды
Qадиабат. =0
Qнеобратимый = T∙∆Sо.с.(Qад. =0) +Qнекомпенсированная
Qнекомпенсированная = T∙∆Sт.с.
Qнеобратимый > Qобратимый
Апотерян. = Qнекомпенс

Ответ:
а) Т=225,8 К (равновесный процесс)
б) Т=237,5 К (неравновесный процесс)
∆Uобратимый
∆Uобр. = T∙∆S обр. – Аобр.
Р=1 атм.
Т=225,8 К
∆Uт.с.необр. <∆Uт.с.,обр.
Р=1 атм.
Т=237,5 К
Аобратимый = Амаксимальная = ∆Uобр.
Qобратимый = T∙∆Sокр.среды = Qадиаб. =0
∆Uт.с.. = ∆Uобратимый = Анеобр. + Qнекомп.
Р=1 атм.
Т=225,8 К
Qнекомп. = T∙∆Sт.с.

Ответ:
а) Т=225,8 К (равновесный процесс)
б) Т=237,5 К (неравновесный процесс)
∆Uобратимый
∆Uобр. = T∙∆S обр. –Аобр.
Р=1 атм.
Т=225,8 К
∆Uт.с.необр. <∆Uт.с.,обр.
Р=1 атм.
Т=237,5 К
Передать в о.с. и повысить энтропию о.с.
Qнекомп. = T∙∆Sт.с.
Р=2 атм.
Т=298 К
Р=2 атм.
Т=298 К
обратимо
необратимо

выводы
Aнеобр. < Aобр
Qнеобр. > Qобр.
∆S необр. > ∆S обр.
∆U < T∙∆Sнеобр. – Анеобр.
∆U = T∙∆Sобр. – Аобр.
При самопроизвольном процессе происходит диссипация энергии: упорядоченная форма обмена энергией (работа) превращается в неупорядоченную форму обмена энергией (теплоту), что является причиной роста энтропии

Статистическое толкование энтропии
Уравнение Больцмана
Постулат Планка
Изменение энтропии в различных термодинамических процессах

События происходят в направлении их большей вероятности, т.е. того состояния, которое может быть реализовано большим числом способов

Система, состоящая из большого числа частиц может быть описана двумя способами:
через интегрированное свойство всей системы в целом;
через свойства каждого из участников ансамбля

Термодинамическая вероятность (W) – это число неповторяющихся микросостояний , которые соответствуют данному макросостоянию вещества
Состояние системы, характеризуемое состоянием каждой входящей в него частицы называют микросостоянием системы
Макросостояние – это состояние вещества, характеризуемое его термодинамическими параметрами
Одному макросостоянию соответствует множество микросостояний вещества
Система может существовать огромным числом способов

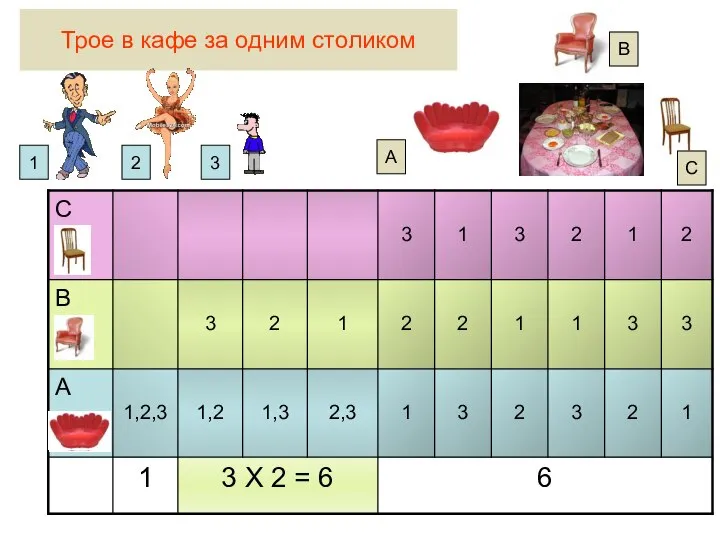
Трое в кафе за одним столиком
1
2
3
А
В
С

Размерность энтропии 1 э.е.= 1 Дж / мольХ К

Энтропия – мера неупорядоченности

Энтропия является функцией состояния системы
Это означает, что энтропия:
Является физическим свойством вещества
Однозначно определена для каждого состояния системы
Изменение энтропии не зависит от пути протекания процесса
Изменение энтропии связано с обменом энергии в форме тепла.
Мера неупорядоченности

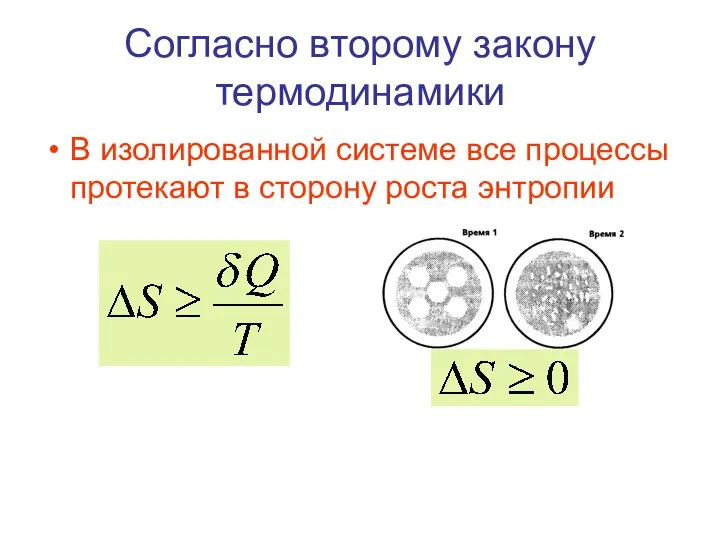
Согласно второму закону термодинамики
В изолированной системе все процессы протекают в сторону роста энтропии

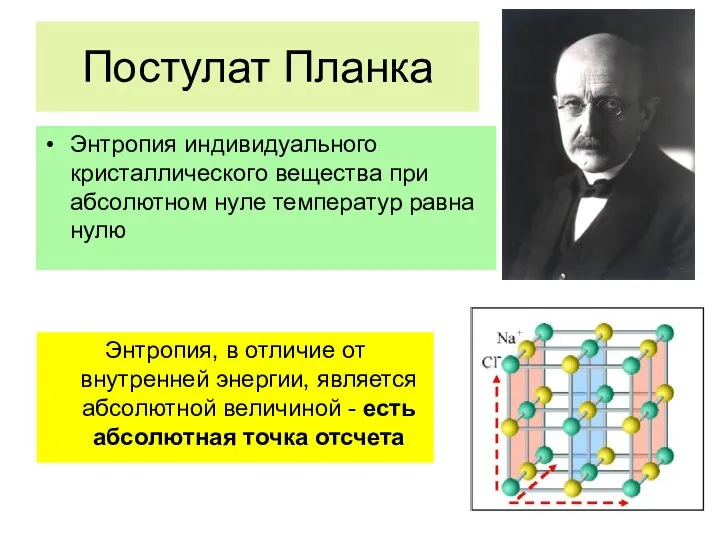
Постулат Планка
Энтропия индивидуального кристаллического вещества при абсолютном нуле температур равна нулю
Энтропия, в отличие от внутренней энергии, является абсолютной величиной - есть абсолютная точка отсчета

Энтропия растет в процессах, сопровождающихся увеличением беспорядка, ростом числа частиц, а также в иных процессах, способствующих увеличению термодинамической вероятности системы
Энтропия растет:
При фазовых переходах плавление – испарение
С ростом температуры
С ростом объема системы
При смешении компонентов
В процессах расширения газа
При растворении
При диссоциации электролитов
С усложнением строения частицы

Энтропия – это:

Энтропия – это:
Свойство, которое имеет абсолютные значения величины (есть ноль отсчета – Постулат Планка)
Экстенсивное свойство: энтропия системы равна сумме энтропий составляющих ее частей.
Величина, характеризующая часть энергии, которая не может быть преобразована в работу при неравновесном процессе – связанной энергии.
Изменение энтропии состоит из двух частей: изменением, обусловленным взаимодействием с ОС и изменением энтропии внутри ТС

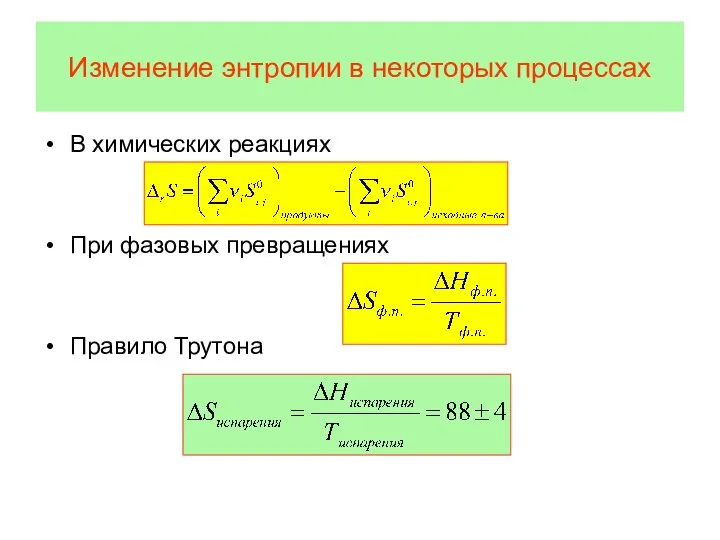
Изменение энтропии в некоторых процессах
В химических реакциях
При фазовых превращениях
Правило Трутона

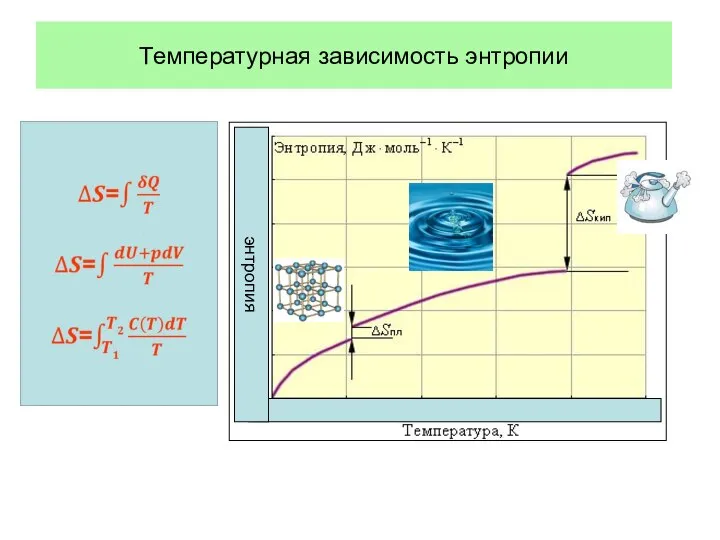
Температурная зависимость энтропии

Фундаментальное уравнение термодинамики
для равновесных процессов
Объединяет первое и второе начало термодинамики

Согласно второму закону термодинамики
В изолированной системе все процессы протекают в сторону роста энтропии

Для неизолированных систем не все так однозначно
Примеры самопроизвольных процессов, сопровождающихся уменьшением энтропии в термодинамической системе:
Система масло – вода после смешения расслаивается
При охлаждении вещество самопроизвольно кристаллизуется, усиливается порядок, энтропия уменьшается
Образование химических связей – уменьшается число частиц, энтропия уменьшается
Испарение воды с мокрых рук: охлаждение рук + испарение воды

Неправильные выводы или что-то упустили из рассмотрения

В системе, но не во Вселенной (как в изолированной системе).
Изменение энтропии состоит из двух частей: изменение, обусловленное взаимодействием ТС с ОС и изменение энтропии внутри самой ТС. Таким образом, порознь каждое из изменений может иметь разный знак, главное, чтобы в сумме они были положительными.
Что же применить в качестве критерия самопроизвольного протекания процесса для конкретной термодинамической системы и конкретных условий ее существования???

Энтропийный и энтальпийный факторы процесса

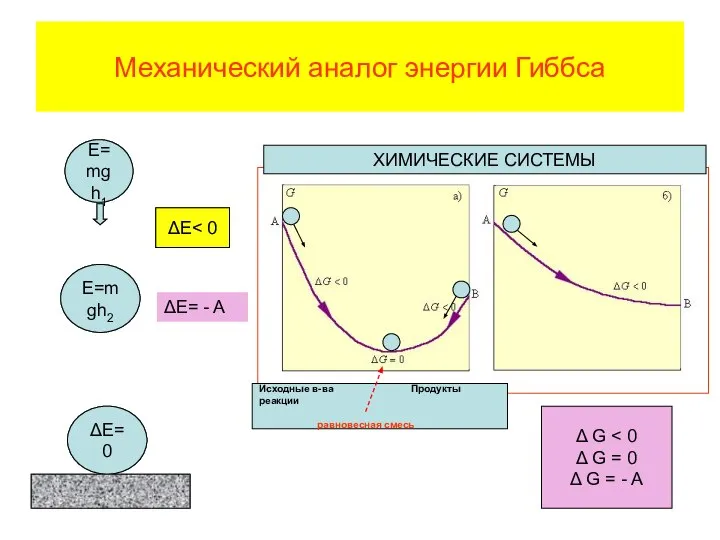
Энергия Гиббса
изобарно-изотермический потенциал
В самопроизвольных процессах система способна совершать работу

Положительным значениям работы соответствуют отрицательные значения изменения энергии Гиббса.
Таким образом, для изобарно-изотермических условий проведения процесса критерием направления самопроизвольного протекания процесса является условие убыли энергии Гиббса, т.е. условие
В самопроизвольных процессах система способна совершать работу!

Механический аналог энергии Гиббса
Δ G < 0
Δ G = 0
Δ G = - A

Энергия Гельмгольца
изохорно-изотермический потенциал

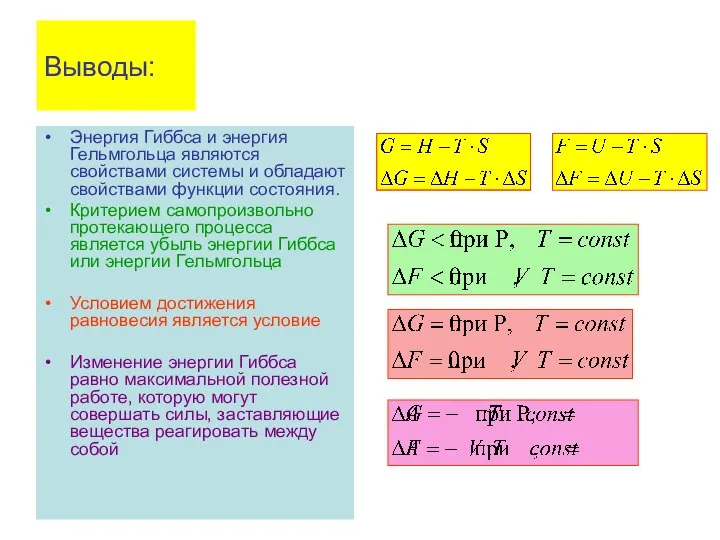
Выводы:
Энергия Гиббса и энергия Гельмгольца являются свойствами системы и обладают свойствами функции состояния.
Критерием самопроизвольно протекающего процесса является убыль энергии Гиббса или энергии Гельмгольца
Условием достижения равновесия является условие
Изменение энергии Гиббса равно максимальной полезной работе, которую могут совершать силы, заставляющие вещества реагировать между собой

Выводы:
Энергия Гиббса (энергия Гельмгольца) учитывает обе тенденции - энтальпийную и энтропийную составляющие самопроизвольно протекающего процесса.
Чем в большей степени в процессе изменяется энергия Гиббса (энергия Гельмгольца), тем в более термодинамически устойчивое состояние переходит система
Нельзя отдельно рассматривать изменение энтальпии или энтропии при определении направления протекания процесса, а следует рассматривать изменение

Это означает, что:
1. в самопроизвольных процессах не всегда реализуются, как благоприятные, оба фактора – и энтальпийный и энтропийный
2. с помощью изменения температуры можно заставить протекать процессы, которые при комнатной температуре как самопроизвольные не идут.

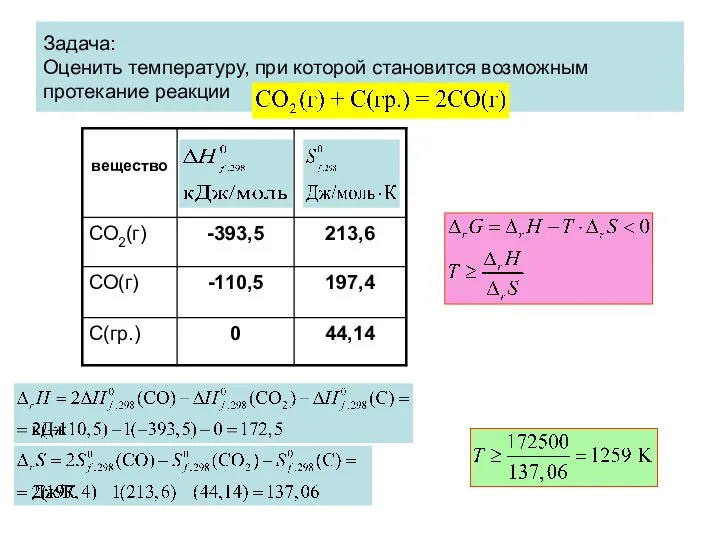
Задача:
Оценить температуру, при которой становится возможным протекание реакции

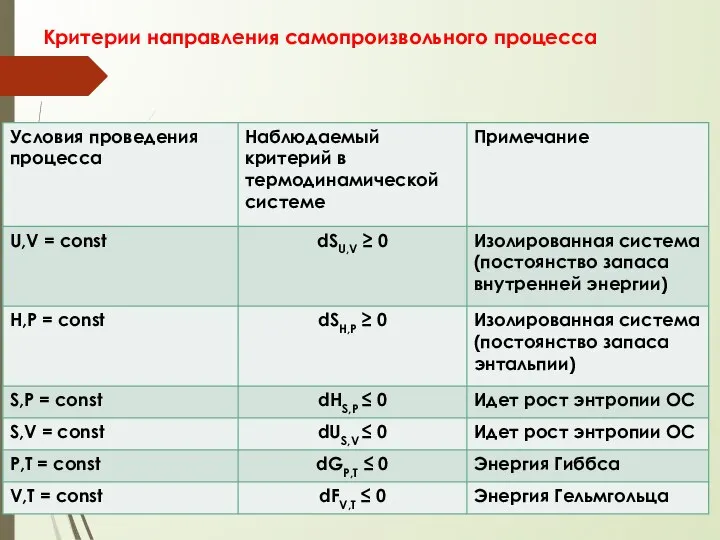
Условия протекания самопроизвольного процесса при условии постоянства в системе:
1) внутренней энергии и объема
2) энтальпии и давления
Критерий – рост энтропии
(что уже не вызывает удивления)

Изохорно - изоэнтропийный процесс
Изобарно – изоэнтропийный процесс

Вспомним
Ответ:
а) Т=225,8 К (равновесный процесс)
б) Т=237,5 К (неравновесный процесс)
∆Uобратимый
∆Uобр. = T∙∆S обр. –Аобр.
Р=1 атм.
Т=225,8 К,
V, S
∆Uт.с.необр. <∆Uт.с.,обр.
Р=1 атм.
Т=237,5 К
Передать в о.с. и повысить энтропию о.с.
Qнекомп. = T∙∆Sт.с.
Р=2 атм.
Т=298 К
Р=2 атм.
Т=298 К
обратимо
необратимо

Критерии направления самопроизвольного процесса

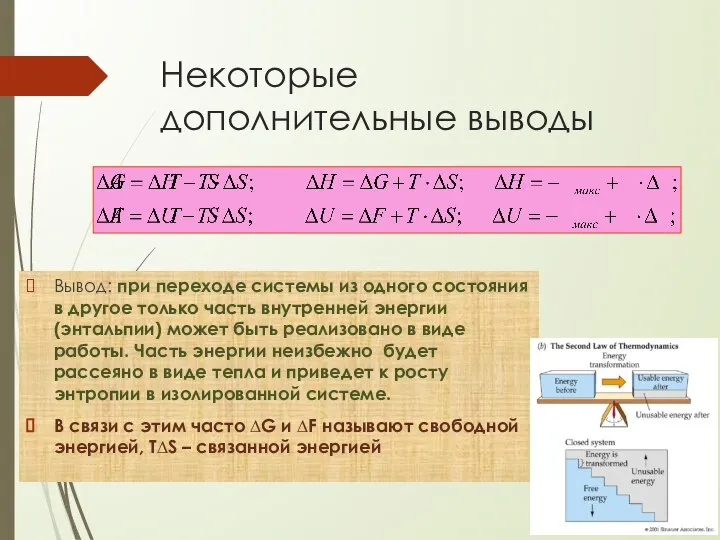
Некоторые дополнительные выводы
Вывод: при переходе системы из одного состояния в другое только часть внутренней энергии (энтальпии) может быть реализовано в виде работы. Часть энергии неизбежно будет рассеяно в виде тепла и приведет к росту энтропии в изолированной системе.
В связи с этим часто ∆G и ∆F называют свободной энергией, T∆S – связанной энергией

Характеристические функции
Термодинамические потенциалы
Характеристической называется такая функция состояния системы, посредством которой или/и посредством ее производной могут быть выражены в явной форме термодинамические свойства системы
В термодинамике наиболее широко используют пять характеристических функций:
Энергия Гиббса (изобарно-изотермический потенциал)
Энергия Гельмгольца (изохорно-изотермический потенциал)
Внутренняя энергия (изохорно-изоэнтропийный потенциал)
Энтальпия (изобарно-изоэнтропийный потенциал)
Энтропия
Первые пять объединены общим названием термодинамических потенциалов

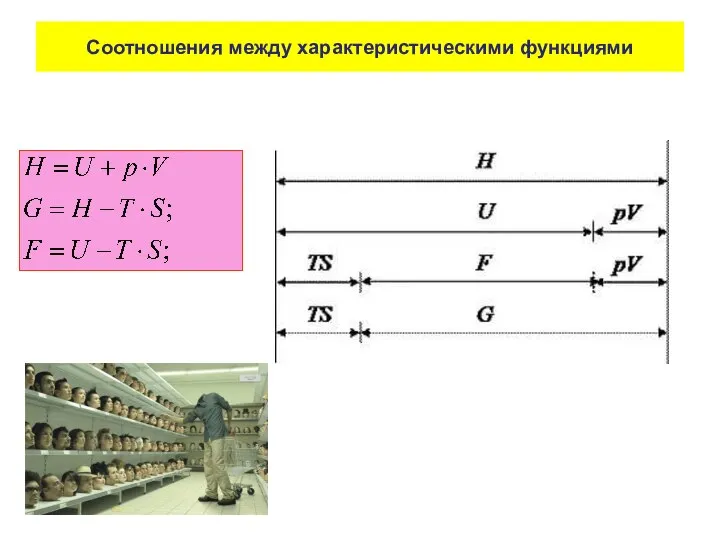
Соотношения между характеристическими функциями

Термодинамические потенциалы:
Являются функциями состояния системы
Позволяют установить направление и пределы самопроизвольного протекания процесса
Позволяют вычислить величины максимальной полезной работы в различных процессах
Выразить различные свойства термодинамической системы

Фундаментальное уравнение термодинамики

Соотношения Максвелла

Задача