Содержание
- 2. 2.1. Первый закон Ньютона. Инерциальные системы В основе так называемой классической или ньютоновской механики лежат три
- 3. Первый закон Ньютона: всякая материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор,
- 4. Оба названных состояния схожи тем, что ускорение тела равно нулю. Поэтому формулировке первого закона можно придать
- 5. Механическое движение относительно, и его характер зависит от системы отсчёта. Первый закон Ньютона выполняется не во
- 6. Система отсчёта, связанная с Землей, строго говоря, неинерциальная, однако эффекты, обусловленные её неинерциальностью (Земля вращается вокруг
- 7. Сущность первого закона Ньютона может быть сведена к трём основным положениям: все тела обладают свойствами инерции;
- 8. 2.2. Масса и импульс тела Воздействие на данное тело со стороны других тел вызывает изменение его
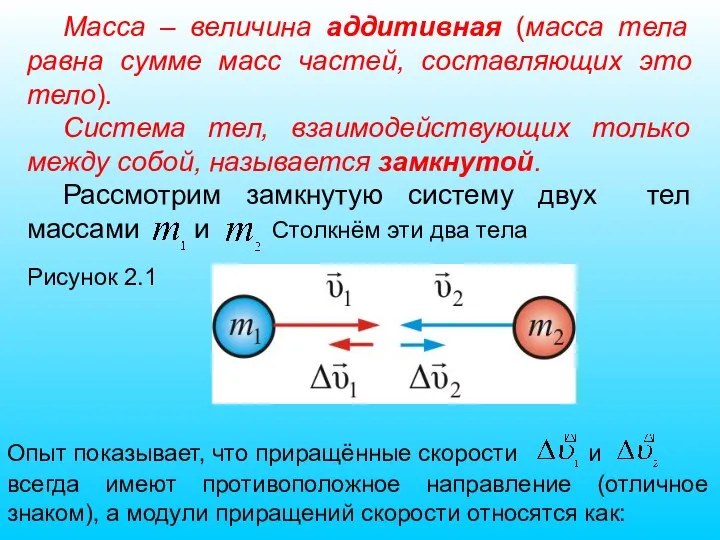
- 9. Масса – величина аддитивная (масса тела равна сумме масс частей, составляющих это тело). Система тел, взаимодействующих
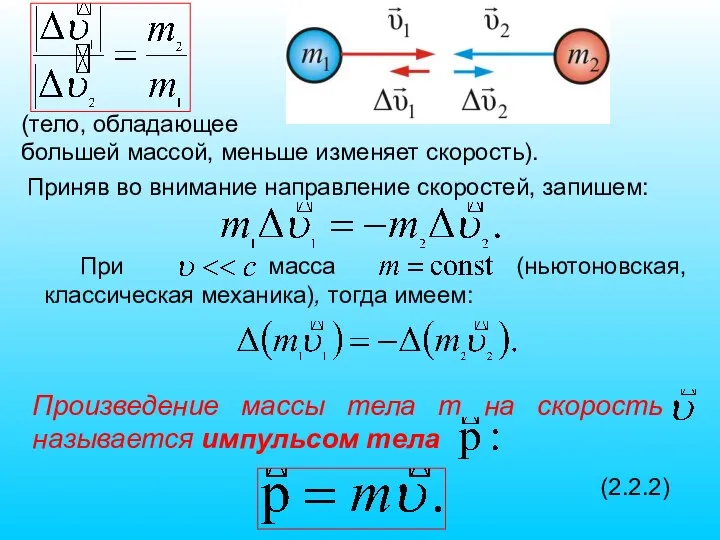
- 10. Приняв во внимание направление скоростей, запишем: При масса (ньютоновская, классическая механика), тогда имеем: Произведение массы тела
- 11. 2.3. Второй закон Ньютона. Математическое выражение второго закона Ньютона: (2.3.1) скорость изменения импульса тела равна действующей
- 12. основное уравнение динамики посту-пательного движения материальной точки. Принцип суперпозиции или принцип независимости действия сил Если на
- 13. Если на материальную точку действует несколько сил, то каждая из них сообщает точке такое же ускорение,
- 14. В системе СИ семь основных единиц (м) – метр, (кг) – килограмм, (с) – секунда, (А)
- 15. 2.4. Третий закон Ньютона
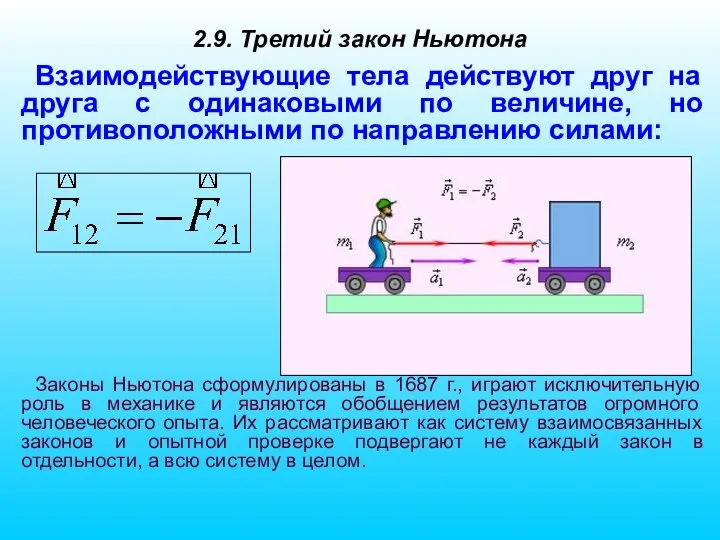
- 16. 2.9. Третий закон Ньютона Взаимодействующие тела действуют друг на друга с одинаковыми по величине, но противоположными
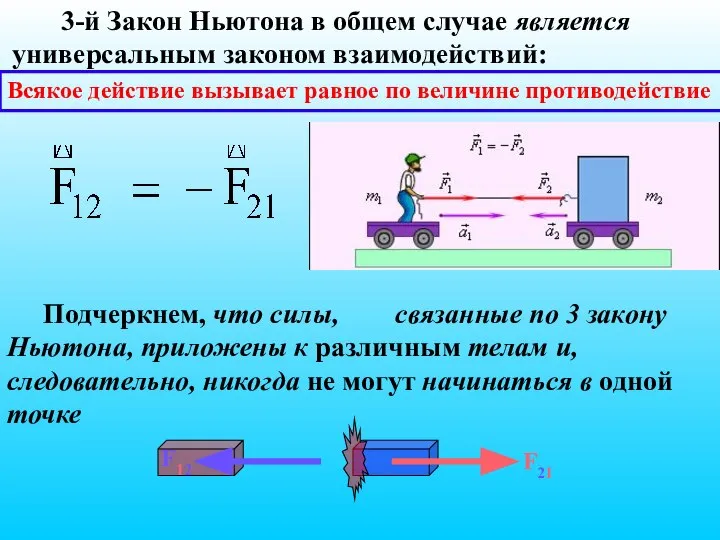
- 17. Всякое действие вызывает равное по величине противодействие 3-й Закон Ньютона в общем случае является универсальным законом
- 18. Законы Ньютона плохо работают при (релятивистская механика) а также, при движении тел очень малых размеров, сравнимых
- 19. 2.5. Импульс произвольной системы тел
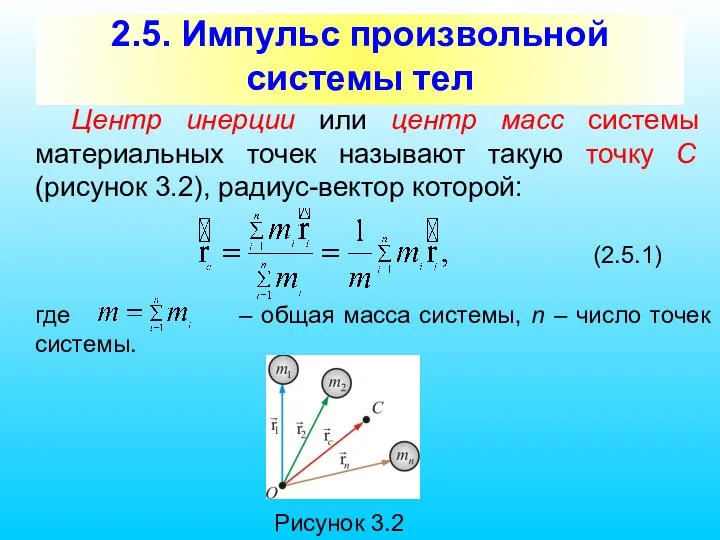
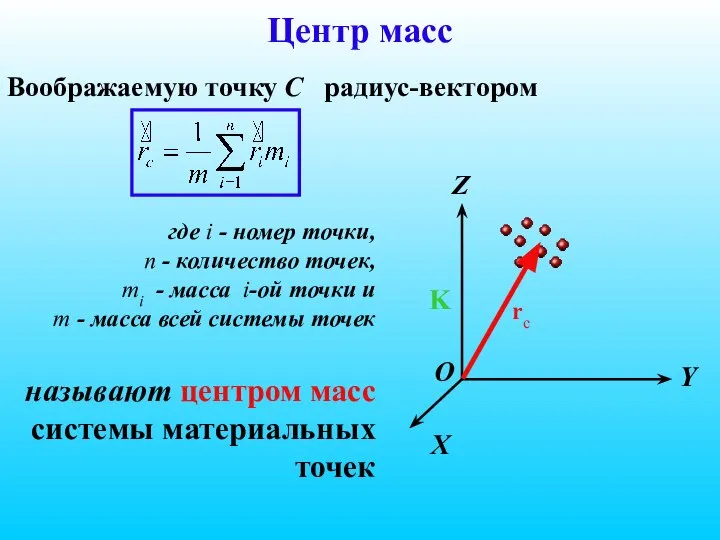
- 20. Центр масс Воображаемую точку С радиус-вектором X Y Z K O rc где i - номер
- 21. При этом не надо путать центр масс с центром тяжести системы – с точкой приложения равнодействующей
- 22. – импульс системы тел, – скорость i-го тела системы. Так как то импульс системы тел можно
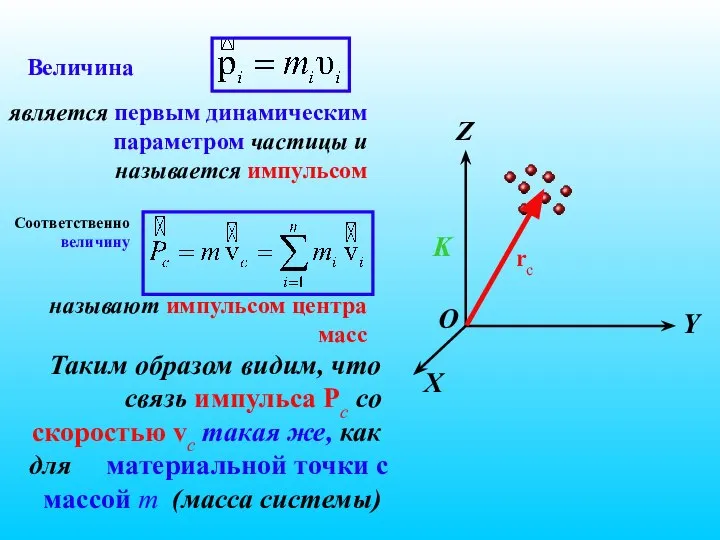
- 23. является первым динамическим параметром частицы и называется импульсом Величина называют импульсом центра масс Соответственно величину X
- 24. 2.6. Основное уравнение динамики поступательного движения произвольной системы тел
- 25. Обозначим – результирующая всех внешних сил приложенных к i-ой точке системы. По второму закону Ньютона можно
- 26. Сложим эти уравнения и сгруппируем попарно силы и По третьему закону Ньютона, поэтому все выражения в
- 27. Скорость изменения импульса системы тел равна главному вектору всех внешних сил, действующих на эту систему. Это
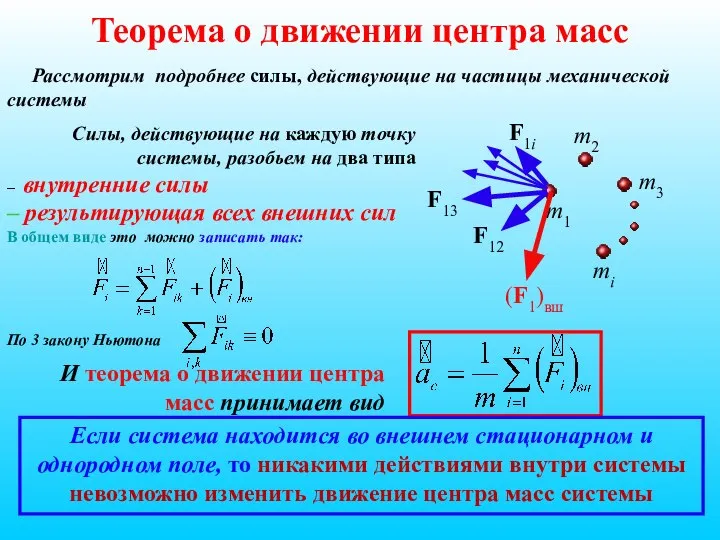
- 28. Центр механической системы движется как материальная точка, масса которой равна массе всей системы, и на которую
- 29. Теорема о движении центра масс Рассмотрим подробнее силы, действующие на частицы механической системы Силы, действующие на
- 30. 2.7. Закон сохранения импульса
- 31. отсюда (2.7.2) Это есть закон сохранения импульса: импульс замкнутой системы не изменяется во времени. Импульс системы
- 32. 2.8. Виды и категории сил в природе Одно из простейших определений силы: влияние одного тела (или
- 33. В настоящее время, различают четыре типа сил или взаимодействий: гравитационные; электромагнитные; сильные (ответственное за связь частиц
- 36. I. Силы Силы трения Силы гравитационные Силы тяжести (вес тела) Силы упругости
- 37. 2.9. Сила тяжести и вес тела Одна из фундаментальных сил – сила гравитации проявляется на Земле
- 38. то есть вес и сила тяжести равны друг другу, но приложены к разным точкам: вес к
- 39. и если наоборот, то Если же тело движется с ускорением то – т.е. наступает состояние невесомости.
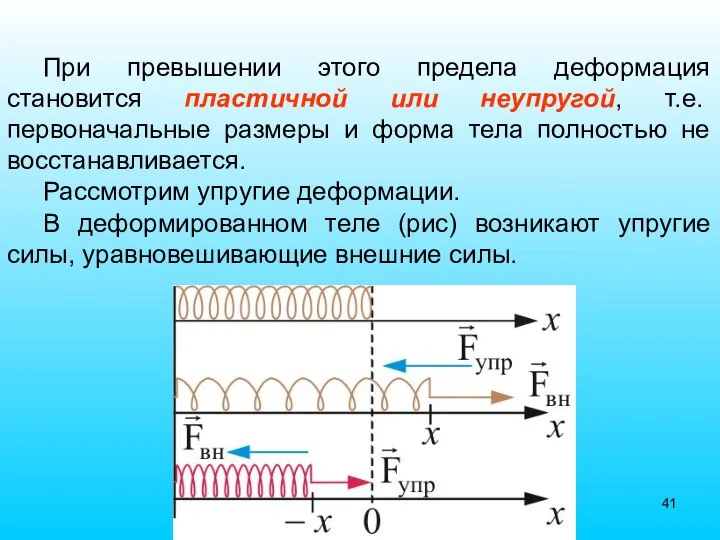
- 40. 2.10. Упругие силы Электромагнитные силы проявляют себя как упругие силы и силы трения. Под действием внешних
- 41. При превышении этого предела деформация становится пластичной или неупругой, т.е. первоначальные размеры и форма тела полностью
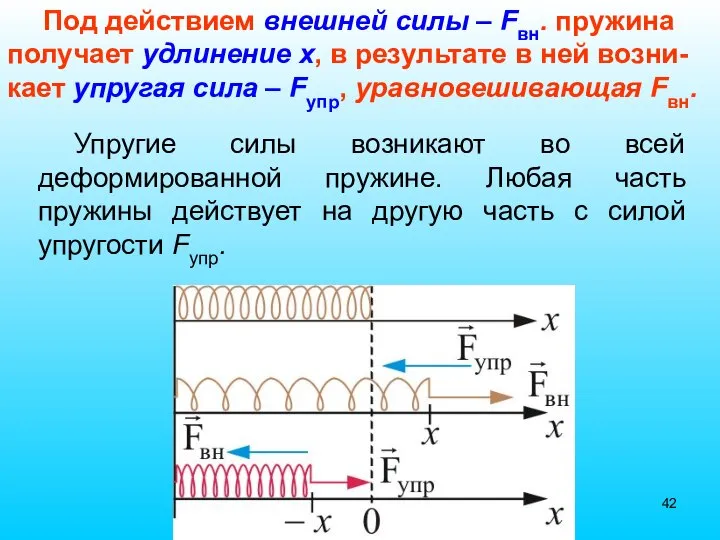
- 42. Упругие силы возникают во всей деформированной пружине. Любая часть пружины действует на другую часть с силой
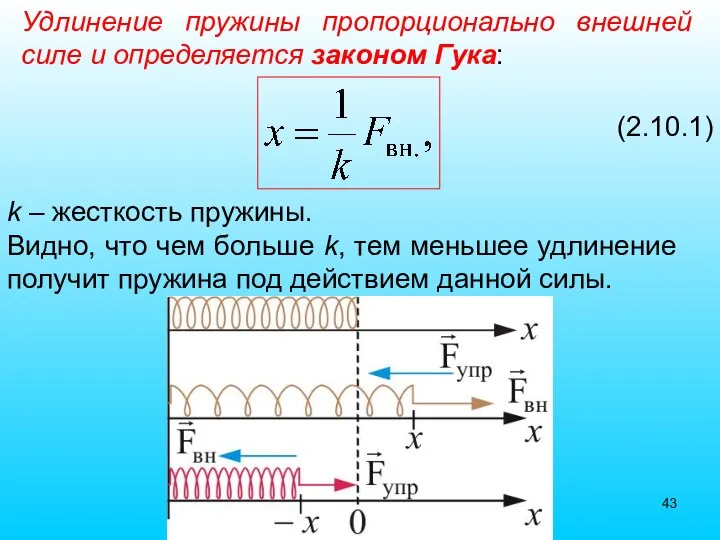
- 43. Удлинение пружины пропорционально внешней силе и определяется законом Гука: (2.10.1) k – жесткость пружины. Видно, что
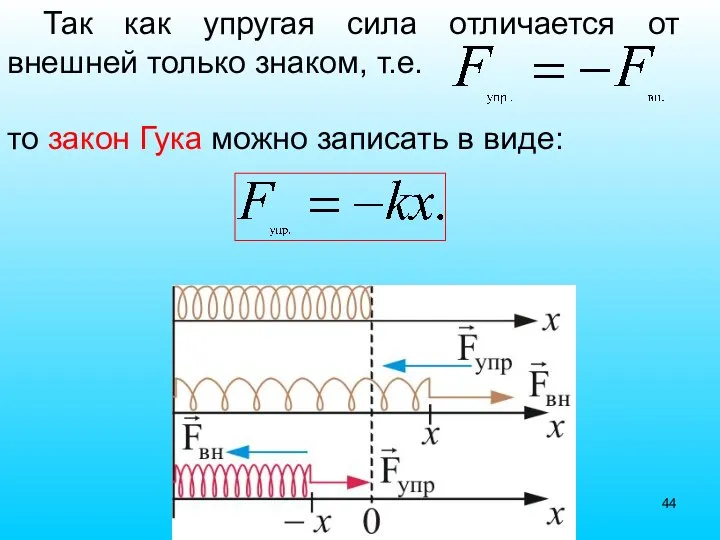
- 44. Так как упругая сила отличается от внешней только знаком, т.е. то закон Гука можно записать в
- 45. Тогда полная работа, которая совершена пружиной, равна: Потенциальная энергия упругой пружины равна работе, совершенной над пружиной.
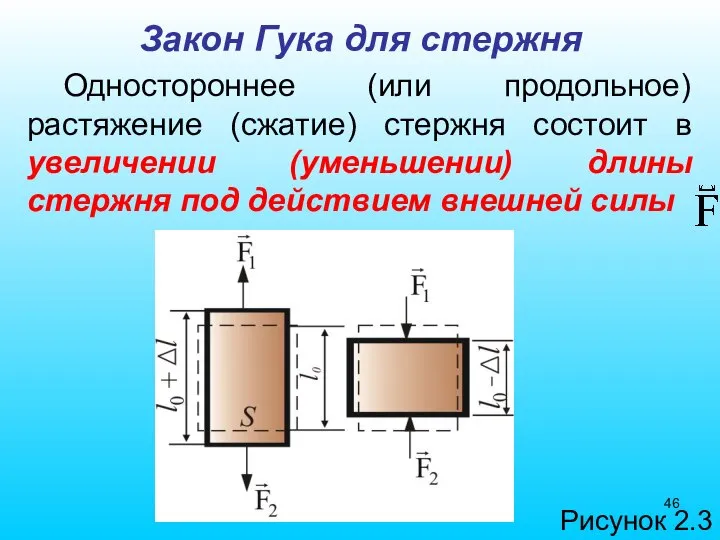
- 46. Закон Гука для стержня Одностороннее (или продольное) растяжение (сжатие) стержня состоит в увеличении (уменьшении) длины стержня
- 47. Такая деформация приводит к возникновению в стержне упругих сил, которые принято характеризовать напряжением σ: Здесь –
- 48. Коэффициент пропорциональности k, как и в случае пружины, зависит от свойств материала и длины стержня. Доказано,
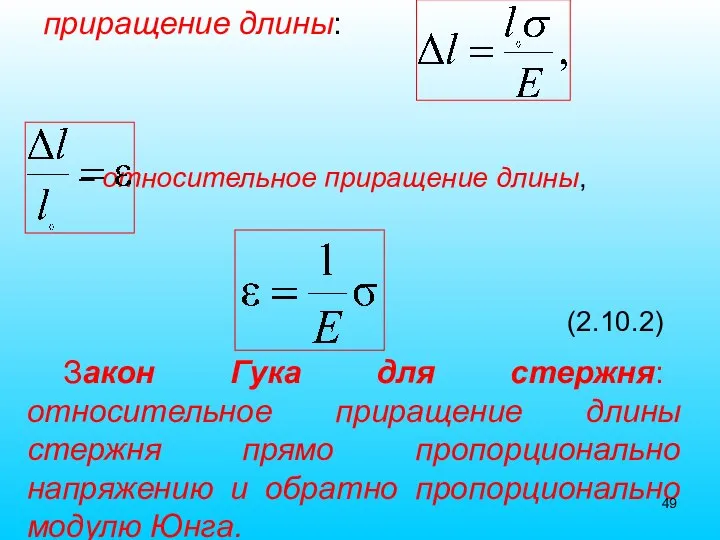
- 49. – относительное приращение длины, (2.10.2) Закон Гука для стержня: относительное приращение длины стержня прямо пропорционально напряжению
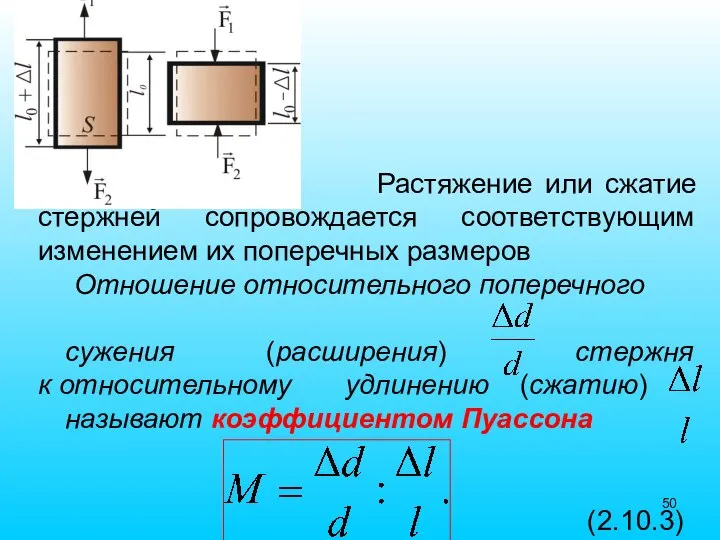
- 50. Растяжение или сжатие стержней сопровождается соответствующим изменением их поперечных размеров Отношение относительного поперечного сужения (расширения) стержня
- 51. Объемная плотность потенциальной энергии тела при растяжении (сжатии) определяется удельной работой по преодолению упругих сил Aупр
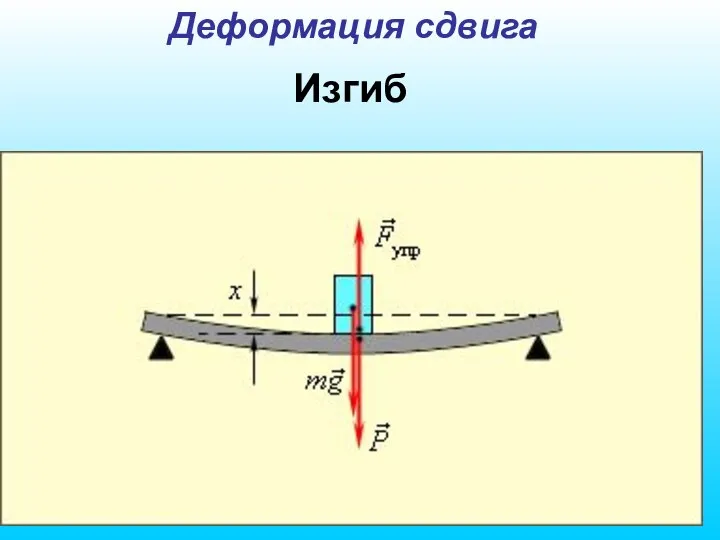
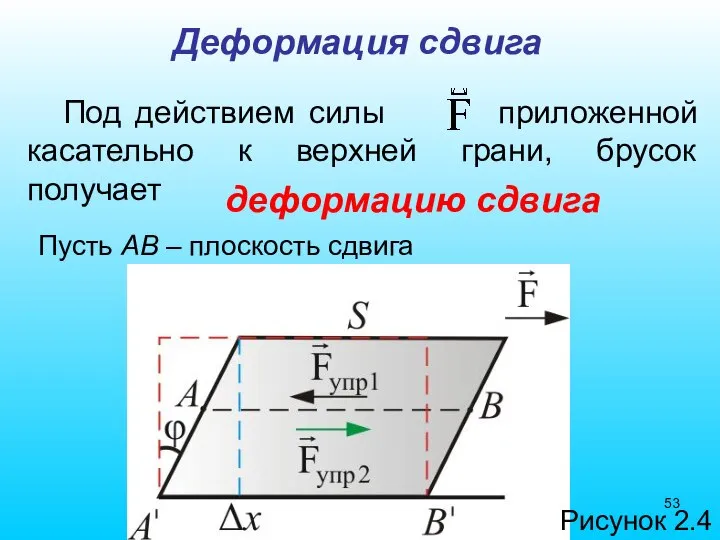
- 52. Изгиб Деформация сдвига
- 53. Деформация сдвига Под действием силы приложенной касательно к верхней грани, брусок получает деформацию сдвига Пусть АВ
- 54. 2.11. Силы трения Трение подразделяется на внешнее и внутреннее. Внешнее трение возникает при относительном перемещении двух
- 55. Жидким (вязким) называется трение между твердым телом и жидкой или газообразной средой или ее слоями. Сухое
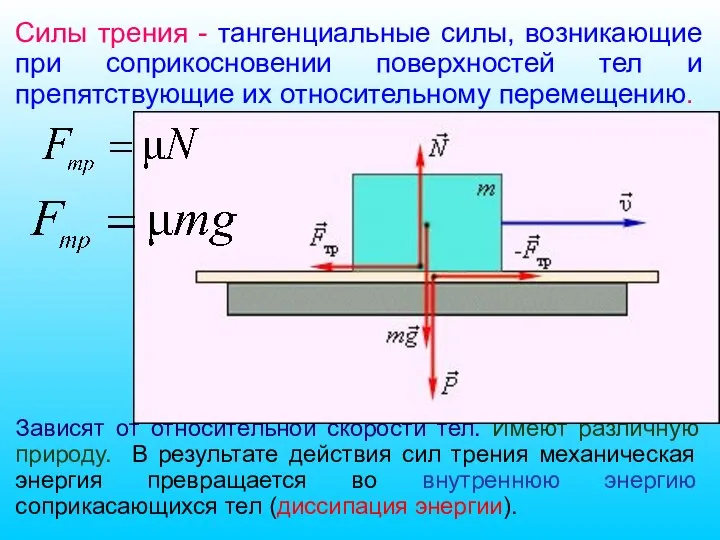
- 56. Силы трения - тангенциальные силы, возникающие при соприкосновении поверхностей тел и препятствующие их относительному перемещению. Зависят
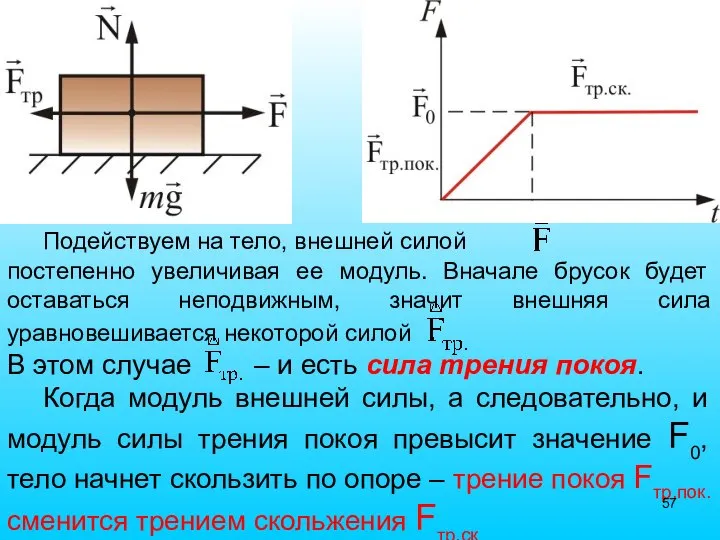
- 57. Подействуем на тело, внешней силой постепенно увеличивая ее модуль. Вначале брусок будет оставаться неподвижным, значит внешняя
- 58. Установлено, что максимальная сила трения покоя не зависит от площади соприкосновения тел и приблизительно пропорциональна модулю
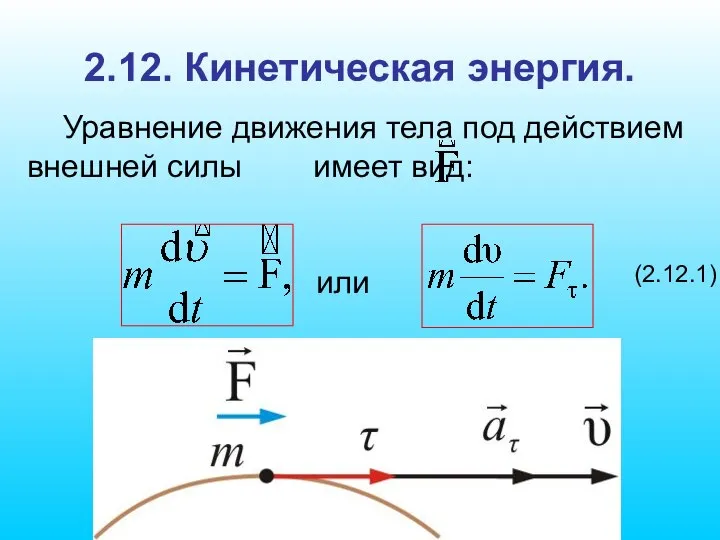
- 60. 2.12. Кинетическая энергия. Уравнение движения тела под действием внешней силы имеет вид: или (2.12.1)
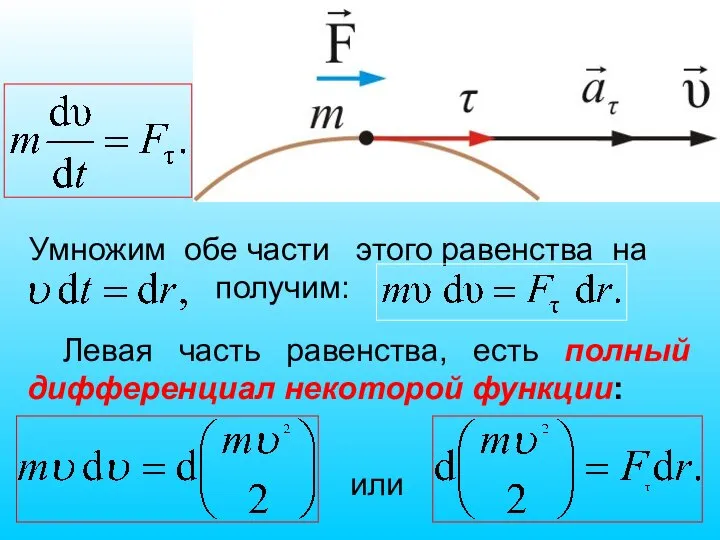
- 61. Умножим обе части этого равенства на получим: Левая часть равенства, есть полный дифференциал некоторой функции: или
- 62. Т.о. Если система замкнута, то и тогда и Если полный дифференциал некоторой функции, описывающей поведение системы
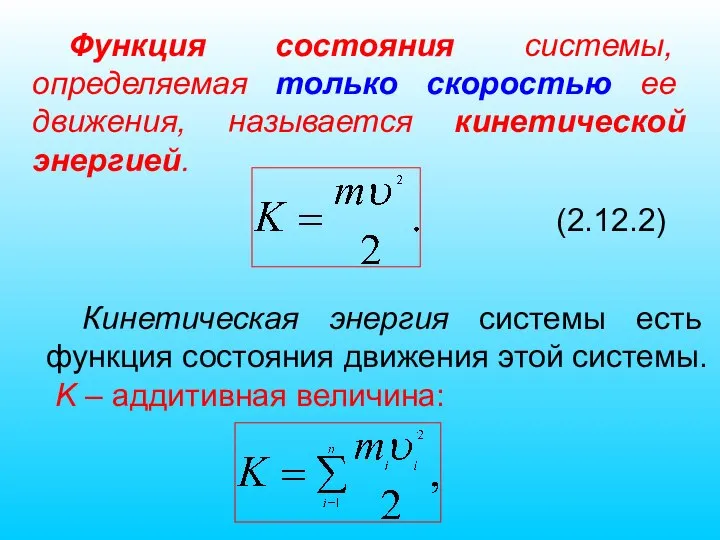
- 63. Функция состояния системы, определяемая только скоростью ее движения, называется кинетической энергией. (2.12.2) Кинетическая энергия системы есть
- 64. Энергия измеряется в СИ в единицах произведения силы на расстояние, т.е. в ньютонах на метр: Кроме
- 65. отсюда Связь кинетической энергии с импульсом p. Т.к.
- 66. Связь кинетической энергии с работой. Если постоянная сила действует на тело, то оно будет двигаться в
- 67. Следовательно, работа силы приложенной к телу на пути r численно равна изменению кинетической энергии этого тела:
- 68. Мощность есть работа, совершаемая в единицу времени. Мгновенная мощность или Средняя мощность Измеряется мощность в ваттах.
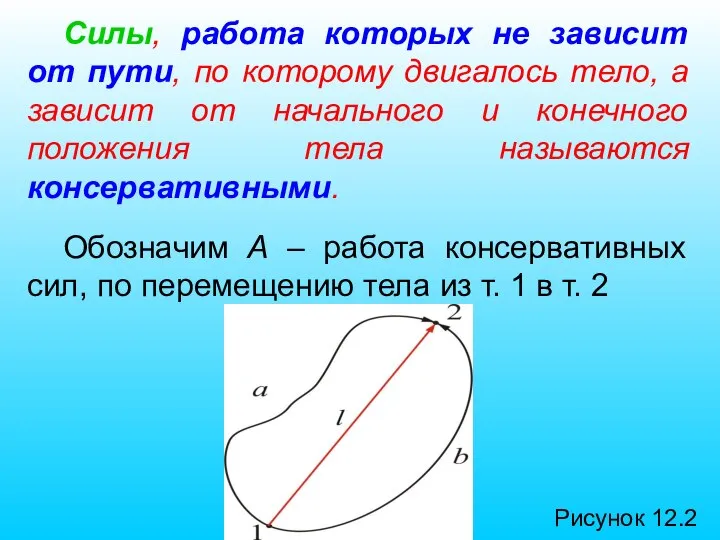
- 69. Силы, работа которых не зависит от пути, по которому двигалось тело, а зависит от начального и
- 70. Изменение направления движения на противоположное – вызывает изменение знака работы консервативных сил. Отсюда следует, что работа
- 71. Если циркуляция какого-либо вектора силы равна нулю, то эта сила консервативна. Консервативные силы: сила тяжести, электростатические
- 72. 2.13. Потенциальная энергия Если на систему материальных тел действуют консервативные силы, то можно ввести понятие потенциальной
- 73. (2.13.1) здесь потенциальная энергия U (х, у, z) – функция состояния системы, зависящая только от координат
- 74. Потенциальная энергия упругой деформации (пружины) Найдём работу, совершаемую при деформации упругой пружины. Сила упругости Сила непостоянна,
- 75. 2.14. Закон сохранения механической энергии Закон сохранения сводит воедино результаты, полученные нами раньше. В сороковых годах
- 76. Для консервативной системы частиц полная энергия системы: Для механической энергии закон сохранения звучит так: полная механическая
- 77. Для замкнутой системы, т.е. для системы на которую не действуют внешние силы, можно записать: (2.14.2) т.е.
- 78. Если в замкнутой системе действуют неконсервативные силы, то полная механическая энергия системы не сохраняется – частично
- 79. Применение законов сохранения . Абсолютно упругий центральный удар При абсолютно неупругом ударе закон сохранения механической энергии
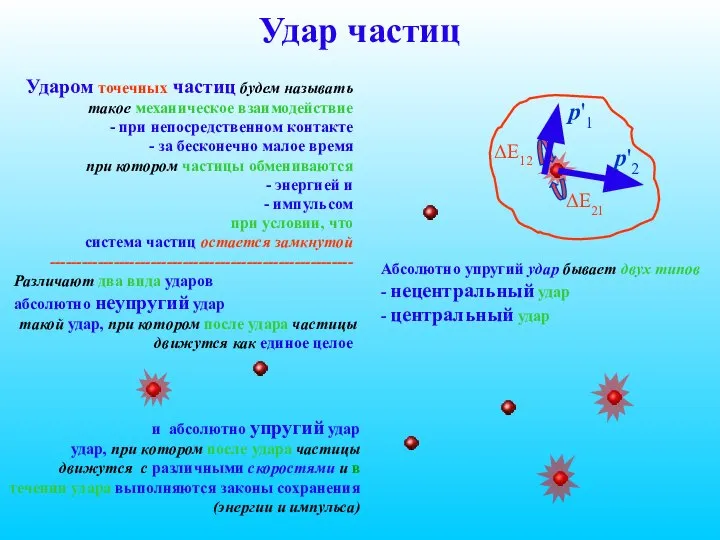
- 80. Удар частиц Ударом точечных частиц будем называть такое механическое взаимодействие - при непосредственном контакте - за
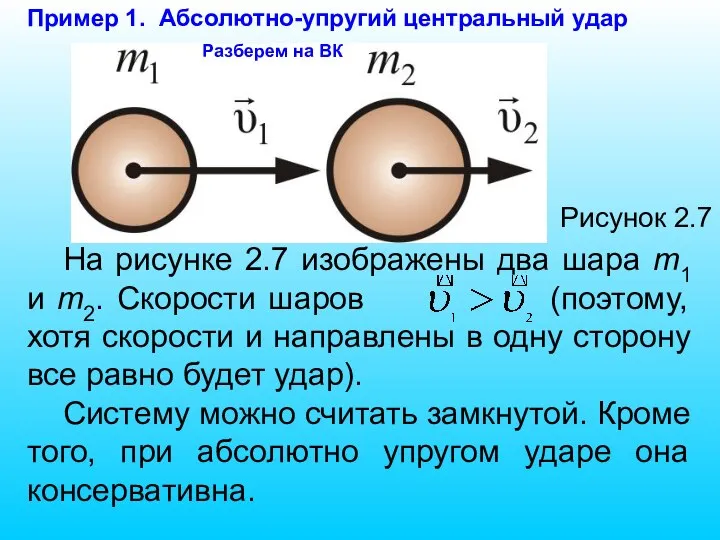
- 81. Рисунок 2.7 На рисунке 2.7 изображены два шара m1 и m2. Скорости шаров (поэтому, хотя скорости
- 82. Обозначим и – скорости шаров после их столкновения. В данном случае можно воспользоваться законом сохранения механической
- 83. Пример 2. Абсолютно упругий удар шара о неподвижную массивную стенку. Стенку можно рассматривать как неподвижный шар
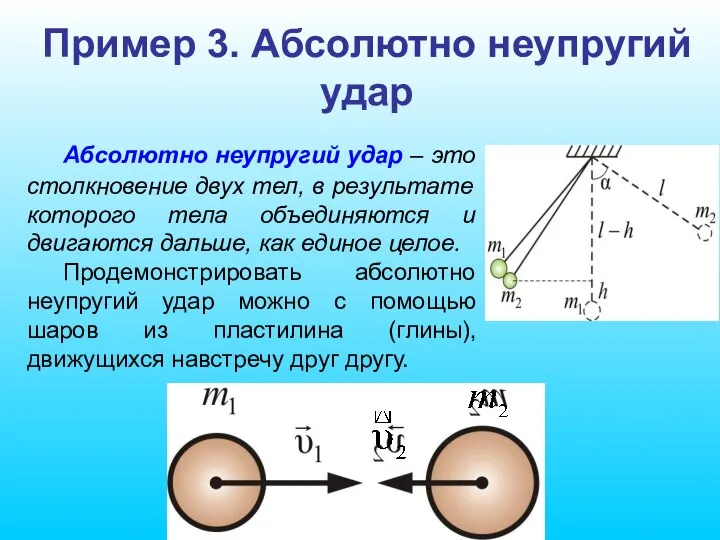
- 84. Пример 3. Абсолютно неупругий удар Абсолютно неупругий удар – это столкновение двух тел, в результате которого
- 85. Если массы шаров m1 и m2, их скорости до удара то используя закон сохранения импульса, можно
- 86. Если шары двигались навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в
- 87. Так как в процессе соударения шаров между ними действуют силы, зависящие не от самих деформаций, а
- 89. Скачать презентацию



























































 Плавание судов
Плавание судов Агрегатные состояния вещества. Различие в молекулярном строении твердых тел, жидкостей и газов (7 класс)
Агрегатные состояния вещества. Различие в молекулярном строении твердых тел, жидкостей и газов (7 класс) Действие магнитного поля на проводник с током. Сила Ампера. Взаимодействие проводников с током
Действие магнитного поля на проводник с током. Сила Ампера. Взаимодействие проводников с током Законы сохранения
Законы сохранения Электрическое освещение бытовых и промышленных объектов
Электрическое освещение бытовых и промышленных объектов Устройство контроля за поведением ребенка во время сна
Устройство контроля за поведением ребенка во время сна Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью Температура. Тепловое равновесие
Температура. Тепловое равновесие Физика - фундаментальная наука
Физика - фундаментальная наука Абрикосов Алексей Алексеевич
Абрикосов Алексей Алексеевич Аристотель, его вклад в развитие механики
Аристотель, его вклад в развитие механики Презентация на тему Определение положения центра тяжести плоской фигуры
Презентация на тему Определение положения центра тяжести плоской фигуры 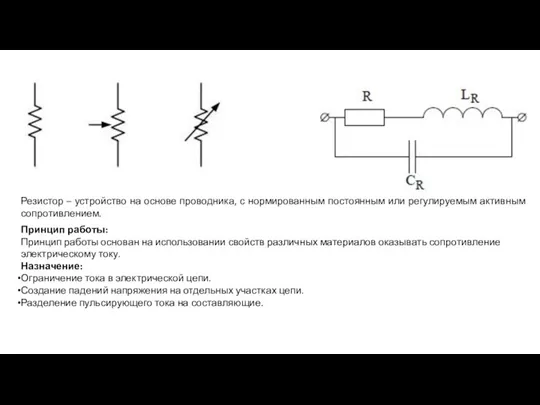 Радиоэлементы. Принцип работы
Радиоэлементы. Принцип работы Условия равновесия твердых тел
Условия равновесия твердых тел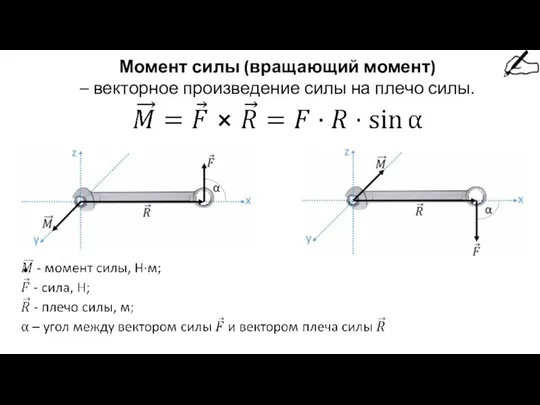 Момент силы (вращающий момент)
Момент силы (вращающий момент) Механические колебания
Механические колебания Электромагнитные колебания
Электромагнитные колебания Развитие представлений о свете
Развитие представлений о свете Сила тока. Напряжение. Сопротивление
Сила тока. Напряжение. Сопротивление Экспериментальные данные и вероятность событий
Экспериментальные данные и вероятность событий Молекулярно-кинетическая теория (МКТ). Масса и размеры молекул
Молекулярно-кинетическая теория (МКТ). Масса и размеры молекул Урок 9п
Урок 9п Статика. Решение задач на равновесие твердого тела
Статика. Решение задач на равновесие твердого тела Расчет характеристик световой волны. Практическая работа №21
Расчет характеристик световой волны. Практическая работа №21 Распространение электромагнитных волн в различных средах
Распространение электромагнитных волн в различных средах Принципиальные и монтажные электросхемы
Принципиальные и монтажные электросхемы Презентация на тему Сложение двух сил, направленных по одной прямой
Презентация на тему Сложение двух сил, направленных по одной прямой  Домашнее задание по физике
Домашнее задание по физике