Определение реакций связей твердого тела

Решение задач на равновесие твердого тела для плоской системы сил

Уравнения равновесия
Ось х не должна быть перпендикулярной к прямой, проходящей через центры А и В
Центры А, В и С не должны лежать на одной прямой
Основная форма условий равновесия (I форма)
II форма условий равновесия
III форма условий равновесия
Три формы уравнений равновесия для ППСС

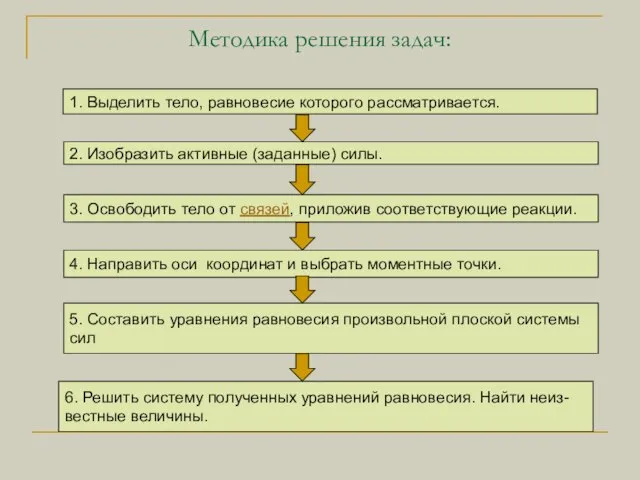
Методика решения задач:
1. Выделить тело, равновесие которого рассматривается.

Рекомендации:
При решении задачи на равновесие тела под дейст-вием произвольной плоской системы сил следует учесть, что:
задача является статически определимой если число неизвестных величин не больше трех (для системы па-раллельных или сходящихся сил не более двух).
натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми.
уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относитель-но точки, где пересекаются линии действия двух реак-ций связей.
при вычислении момента силы часто удобно разло-жить ее на составляющие и , для которых плечи легко определяются, и воспользоваться теоремой Вариньо-на; тогда

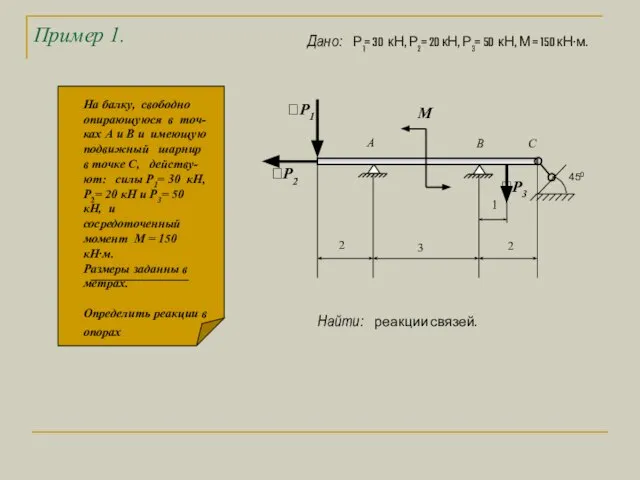
Пример 1.
1
3
2
М
2
А
В
С
Р2
Р1
Р3
На балку, свободно опирающуюся в точ-ках А и В и имеющую подвижный шарнир в точке С, действу-ют: силы Р1= 30 кН, Р2= 20 кН и Р3= 50 кН, и сосредоточенный момент М = 150 кН∙м.
Размеры заданны в метрах.
Определить реакции в опорах
Дано: Р1= 30 кН, Р2= 20 кН, Р3= 50 кН, М = 150 кН∙м.
Найти: реакции связей.

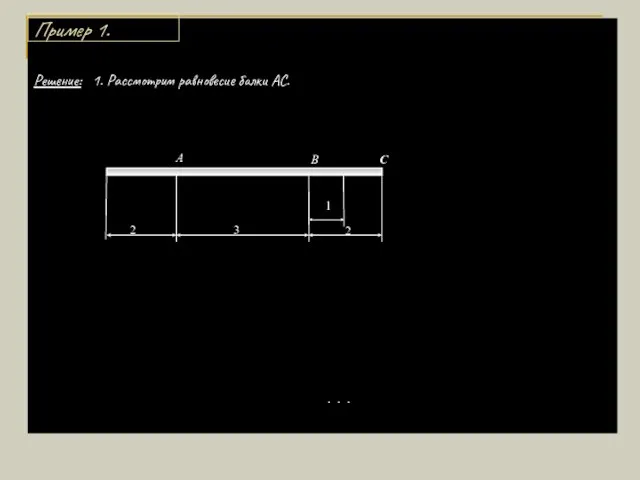
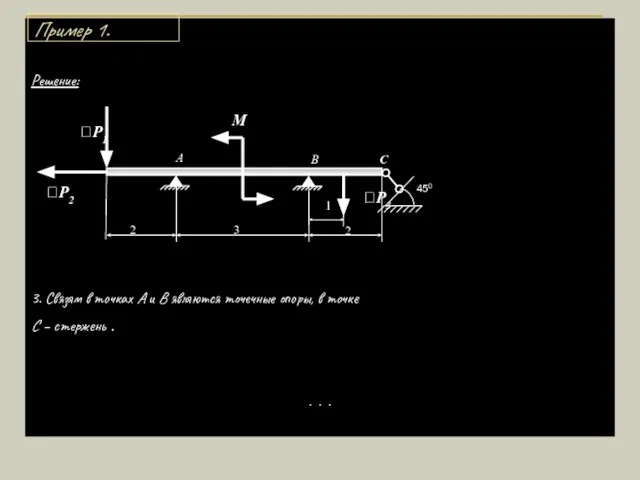
Решение: 1. Рассмотрим равновесие балки АС.
. . .
1
3
2
2
А
В
С
Пример 1.

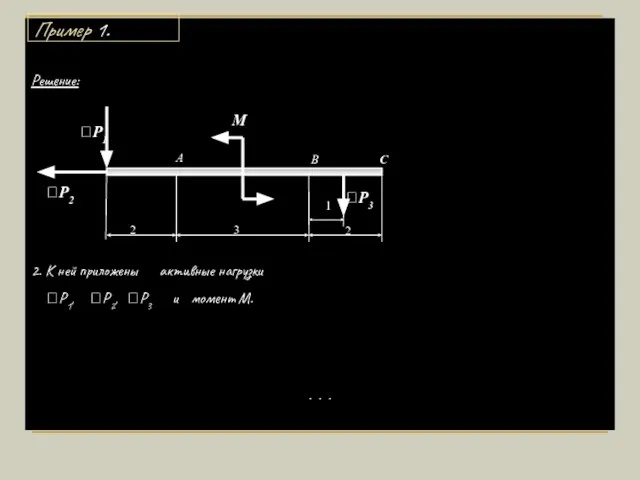
Решение:
2. К ней приложены активные нагрузки
Р1, Р2, Р3 и момент М.
. . .
1
3
2
М
2
А
В
С
Р2
Р1
Р3
Пример 1.

Решение:
3. Связям в точках А и В являются точечные опоры, в точке
С – стержень ..
. . .
1
3
2
М
2
А
В
С
Р2
Р1
Р3
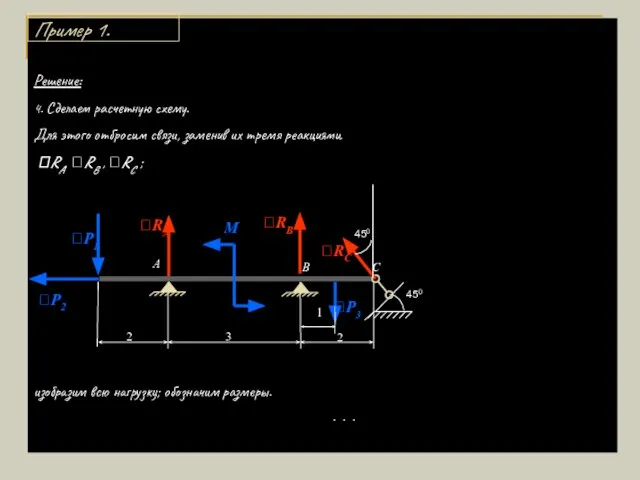
Пример 1.

Решение:
4. Сделаем расчетную схему.
Для этого отбросим связи, заменив их тремя реакциями
RA, RB , RC ;
изобразим всю нагрузку; обозначим размеры.
. . .
Пример 1.
1
3
2
М
2
А
В
С
Р2
Р1
Р3
RA
RB
RC
450

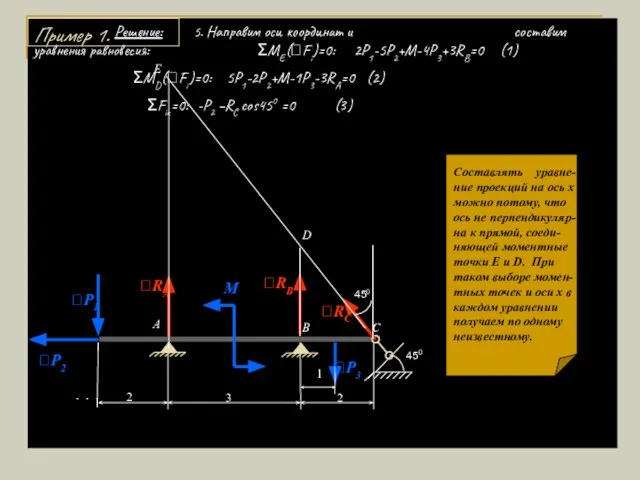
Решение: 5. Направим оси координат и составим уравнения равновесия: ΣМЕ(Fi)=0: 2P1-5P2+M-4P3+3RB=0 (1) ΣМD(Fi)=0: 5P1-2P2+M-1P3-3RA=0 (2)
ΣFix=0: -P2 –RC cos450 =0 (3)
. . .
Пример 1.
1
3
2
М
2
А
В
С
Р2
Р1
Р3
RA
RB
RC
450
E
D
Составлять уравне-ние проекций на ось x можно потому, что ось не перпендикуляр-на к прямой, соеди-няющей моментные точки E и D. При таком выборе момен-тных точек и оси х в каждом уравнении получаем по одному неизвестному.

Решение:
6. Решая полученные уравнения (1), (2), (3) относительно искомых реакций, получим:
RB = (-2P1+5P2-M+4P3)/3 = 30 кН
RA = (5P1-2P2+M-P3)/3 = 70 кН
RC = -P2 / cos450 = 28,28 кН
. . .
Пример 1.