Ауырлық центрі

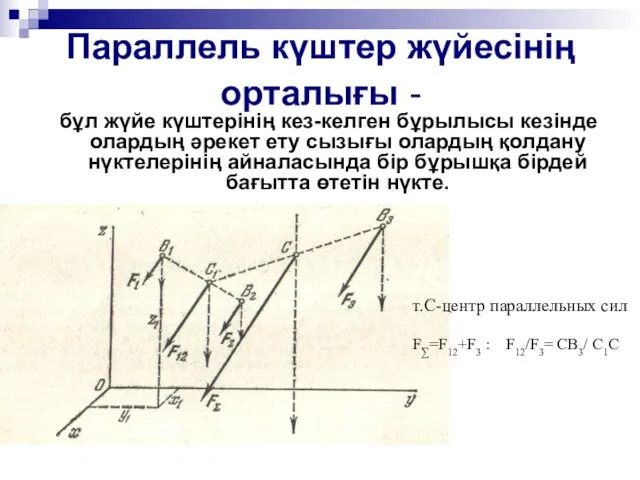
Параллель күштер жүйесінің орталығы -
бұл жүйе күштерінің кез-келген бұрылысы кезінде олардың әрекет ету сызығы олардың қолдану нүктелерінің айналасында бір бұрышқа бірдей бағытта өтетін нүкте.
т.С-центр параллельных сил
F∑=F12+F3 : F12/F3= CВ3/ С1C

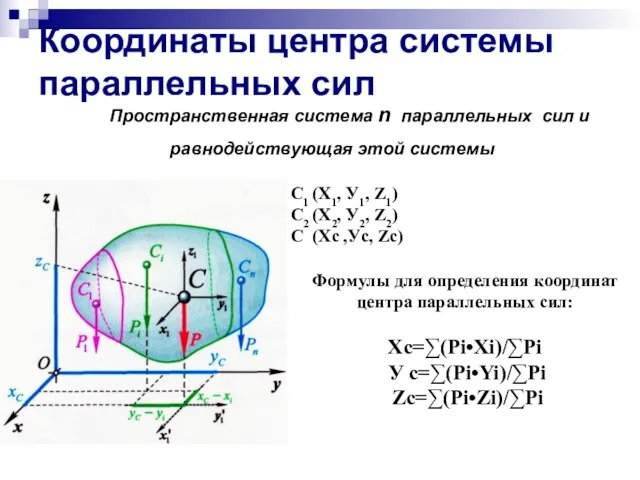
Координаты центра системы параллельных сил
Пространственная система n параллельных сил и равнодействующая этой системы
F2
Формулы для определения координат центра параллельных сил:
Xc=∑(Рi•Xi)/∑Рi
У c=∑(Рi•Yi)/∑Рi
Zc=∑(Рi•Zi)/∑Рi
С1 (Х1, У1, Z1)
С2 (Х2, У2, Z2)
C (Хc ,Уc, Zc)

Ауырлық орталығының орнын анықтау
Ауырлық күші немесе дене салмағы-дененің жерге тартылатын күші.
Кез-келген денені белгілі бір салмағы бар элементар бөлшектер түрінде ұсынуға болады.
Әрбір элементар бөлшектің ауырлық күші жердің центріне бағытталған және параллель күштер жүйесін құрайды.
Осылайша, дененің ауырлық орталығы-дененің барлық элементар бөлшектерінің параллель ауырлық күштерінің центрі.
Ауырлық орталығы-дененің өзінде немесе денеден тыс жерде орналасуы мүмкін геометриялық нүкте( саңылауы бар цилиндр).
Бұл кезде шартты түрде бүкіл дененің салмағы шоғырланған деп саналады.

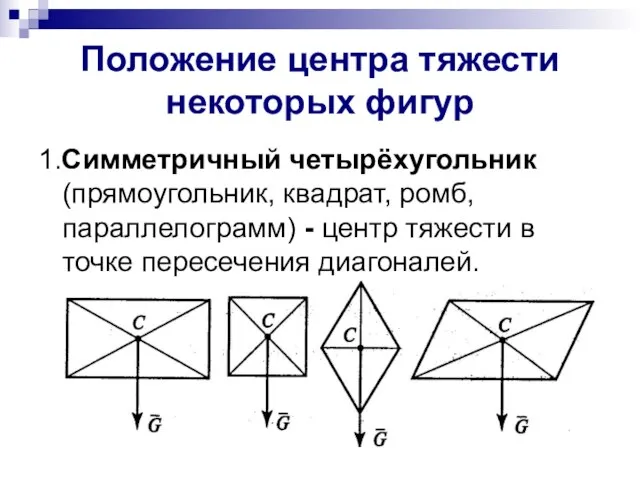
Положение центра тяжести некоторых фигур
1.Симметричный четырёхугольник (прямоугольник, квадрат, ромб, параллелограмм) - центр тяжести в точке пересечения диагоналей.

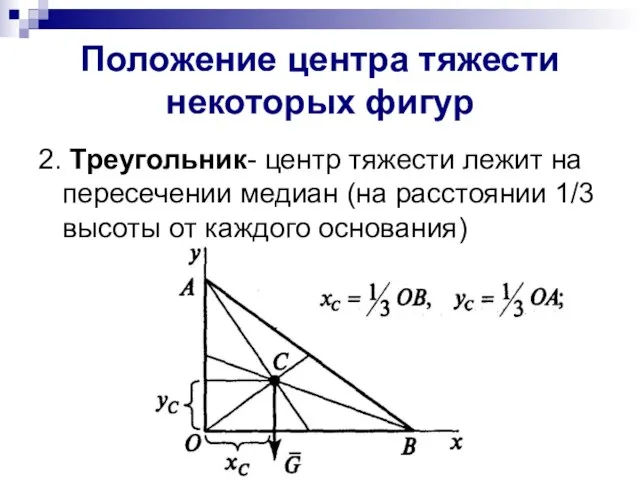
Положение центра тяжести некоторых фигур
2. Треугольник- центр тяжести лежит на пересечении медиан (на расстоянии 1/3 высоты от каждого основания)

Положение центра тяжести некоторых фигур
3. Полукруг— центр тяжести в точке с координатами:
а) Xc= R, Уc=4R/3π (рис. а)
б) Xc=4R/3π , Уc=R (рис. б)

Положение центра тяжести некоторых фигур
4. Конус или полная пирамида — центр тяжести на высоты от основания

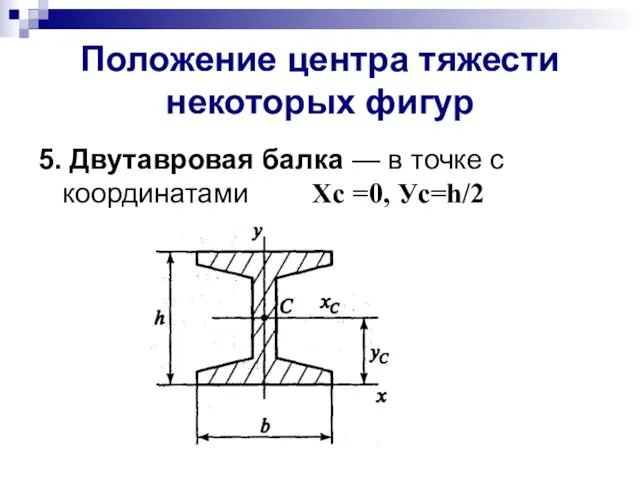
Положение центра тяжести некоторых фигур
5. Двутавровая балка — в точке с координатами Xc =0, Уc=h/2

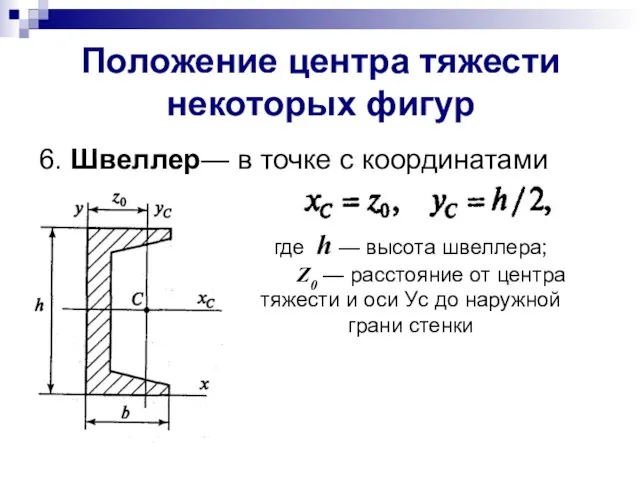
Положение центра тяжести некоторых фигур
6. Швеллер— в точке с координатами
где h — высота швеллера;
Z0 — расстояние от центра тяжести и оси Уc до наружной грани стенки

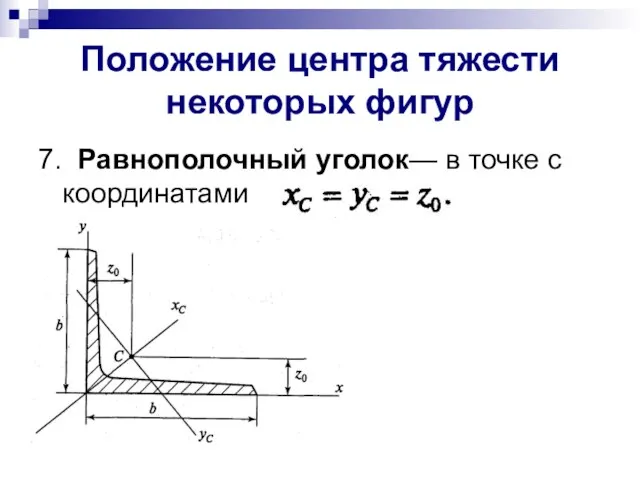
Положение центра тяжести некоторых фигур
7. Равнополочный уголок— в точке с координатами

Методы нахождения центра тяжести
Метод симметрии - этот метод используется для определения центра тяжести однородных симметричных тел и симметричных плоских фигур.
Если однородное тело имеет ось симметрии, то центр тяжести лежит на этой оси
Если две оси симметрии, то центр тяжести находится в точке их пересечения.
Центр тяжести тела вращения лежит на оси вращения.

Методы нахождения центра тяжести
Если плоская фигура имеет неправильную геометрическую форму, то центр тяжести такой фигуры можно определить двумя способами:
1) практическим методом - подвешивания фигуры на острие;
2) теоретическим методом

2 Теоретические методы
А) Метод разбиения - заключается в том, что тело разбивают на фигуры простейшей геометрической формы. Затем определяется положение центра тяжести и площади каждой элементарной фигуры. Для того чтобы найти координаты центра тяжести заданной сложной фигуры, используются следующие формулы:
Где Ai — площади элементарных фигур, на которые разбита сложная фигура;
Xi, Yi— координаты центра тяжести каждой элементарной фигуры относительно случайных осей x и у.

2 Теоретические методы
Б) Метод отрицательных масс - если тело имеет полости или плоская фигура вырезы, то тело вначале рассматривают как единое целое, а затем при подстановке в формулы полости и вырезы будем подставлять со знаком минус.