Осевое растяжение и сжатие стержней

Продольная деформация
Поперечная деформация
Коэффициент Пуассона
осевое растяжение-сжатие стержней

2.2. Закон Гука
E – модуль упругости (модуль Юнга, жесткость) материала
С учетом
закон Гука можно представить в виде
ЕА – жесткость стержня при осевом растяжении или сжатии
осевое растяжение-сжатие стержней
Между σ и ε (двумя разнородными факторами одного явления) существует связь, называемая законом Гука, который является экспериментальным фактом и на современном языке может быть сформулирован так: малые упругие деформации материала, не зависящие от времени деформирования, пропорциональны соответствующим им напряжениям. В случае линейного напряженного состояния закон Гука определен зависимостью

осевое растяжение-сжатие стержней
2.3. Механические характеристики материала
Диаграммы растяжения образцов

осевое растяжение-сжатие стержней
2.4. Расчеты на прочность при растяжении или сжатии
R – расчетное сопротивление материала
Rн – нормативное сопротивление материала, устанавливаемое нормами
проектирования с учетом условий контроля и статистической изменчивости.
k – коэффициент безопасности (запаса прочности). В частности, может быть:
– для хрупких
Условие прочности при растяжении стержня
-- для пластичных материалов

осевое растяжение-сжатие стержней
В зависимости от постановки задачи различают три вида расчета на прочность, которые для случая растяжения или сжатия стержня сводятся к необходимости удовлетворения следующих неравенств:
1) проверочный, когда известны нагрузки на стержень, его материал (расчетное сопротивление) и размеры поперечного сечения:
2) подбор сечения, когда известны нагрузки и материал:
3) определение допускаемой нагрузки, когда известны размеры стержня и
го материал, а определению подлежит нагрузка. Из условия прочности
стержня определяют [N] – допускаемое значение усилия N:
По [N] находят соответствующее ему допускаемое значение внешних усилий.

Условие статического равновесия отсеченной части, как условие равенства нулю суммы проекций на ось всех сил, действующих на рассматриваемую часть стержня, приводит к равенству
Например:
осевое растяжение-сжатие стержней
2.5. Построение эпюры продольного усилия N

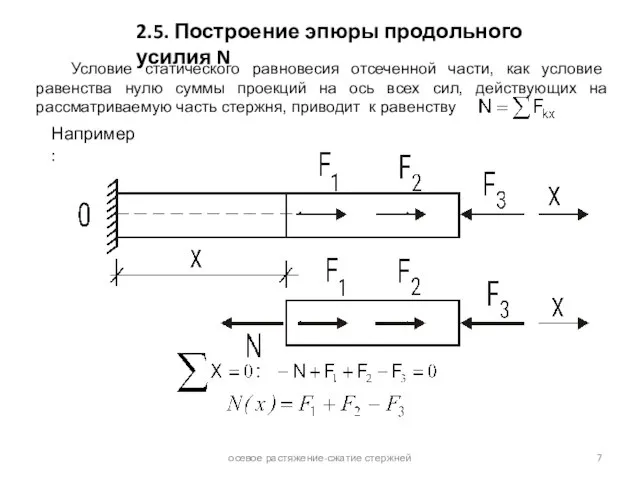
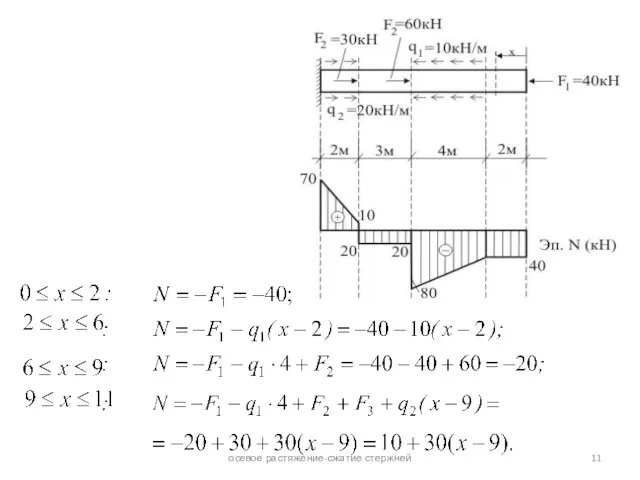
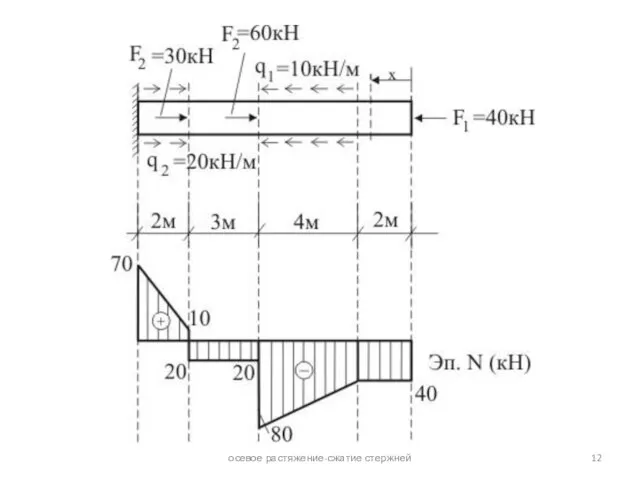
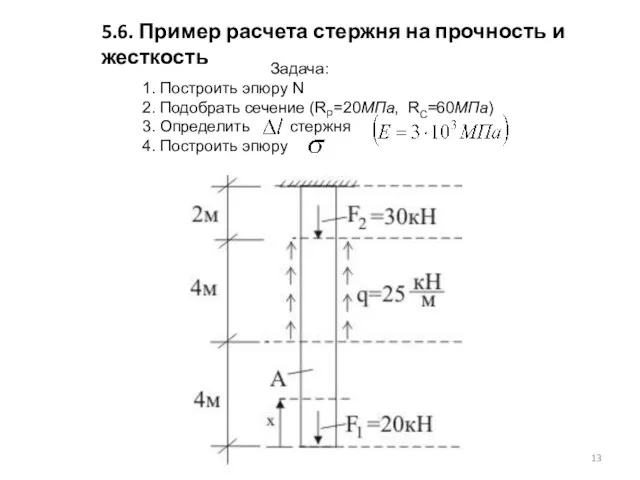
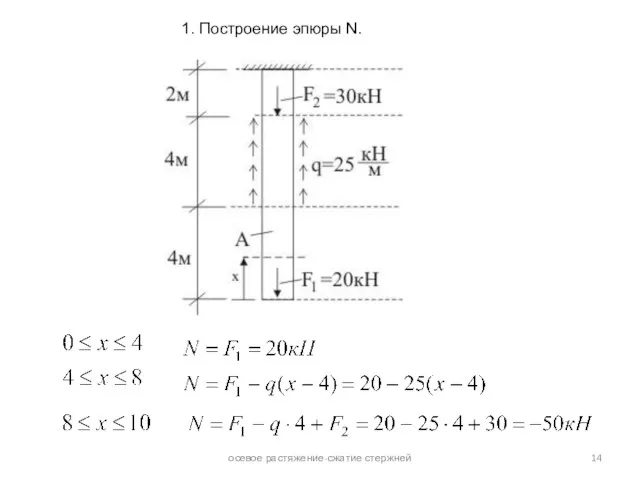
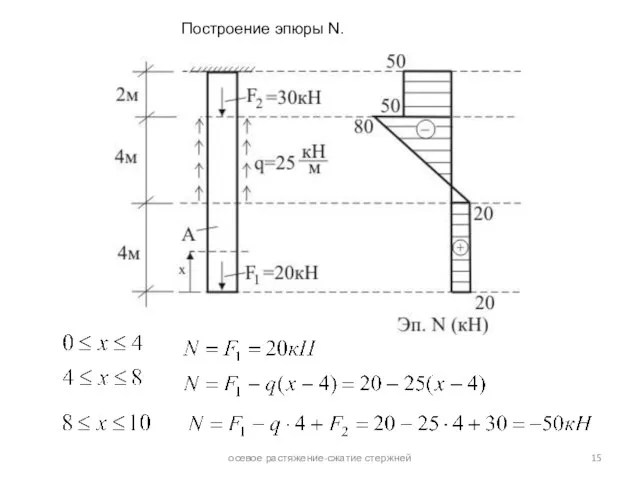
Закон изменения какого-либо усилия по длине стержня в виде графика называют эпюрой этого усилия. Грузовым участком стержня называют его часть, в пределах которой характер действующей нагрузки и его геометрия не меняются. Функциональная зависимость N(x), меняясь от одного грузового участка к другому, на каждом из них сохраняет свой вид.
При исследовании прочности стержня возникает необходимость в знании законов изменения N по его длине. Графические изображения этого закона называют эпюрой продольного усилия.
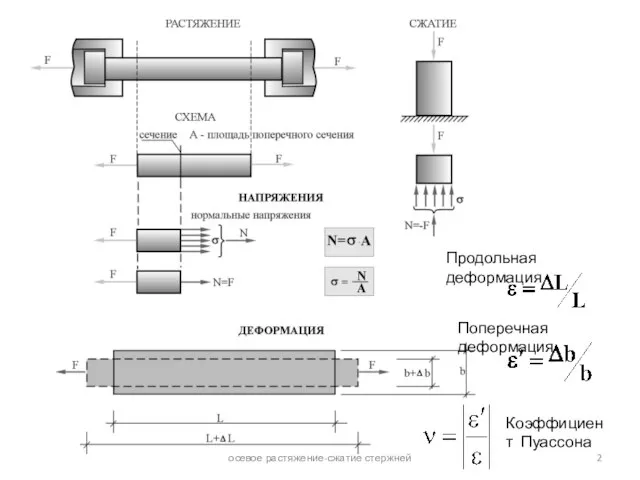
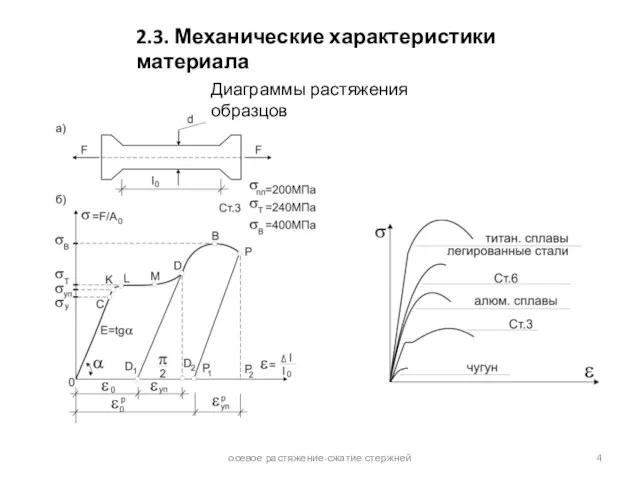
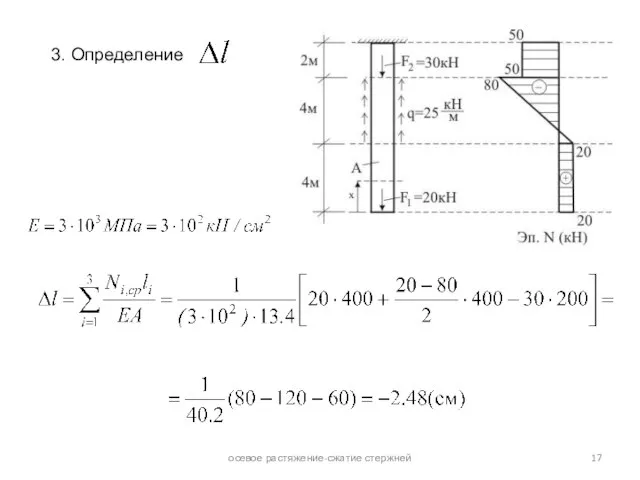
осевое растяжение-сжатие стержней
Величину N в произвольном сечении стержня определяют из условия равновесия его отсеченной части. При этом, согласно закону Ньютона (аксиоме) о равенстве действия и противодействия, не важно равновесие какой из двух частей стержня рассматривать.
N в произвольном сечении стержня численно равно алгебраической сумме проекций на его ось всех внешних сил, приложенных к рассматриваемой (любой из двух) отсеченной части.

осевое растяжение-сжатие стержней
Пример построения эпюры N
Для каждого из 4-х грузовых участков запишем выражения
для продольного усилия N(х).

осевое растяжение-сжатие стержней
:

осевое растяжение-сжатие стержней

осевое растяжение-сжатие стержней

осевое растяжение-сжатие стержней
Задача:
1. Построить эпюру N
2. Подобрать сечение (RP=20МПа, RC=60МПа)
3. Определить стержня
4. Построить эпюру
5.6. Пример расчета стержня на прочность и жесткость

осевое растяжение-сжатие стержней
1. Построение эпюры N.

осевое растяжение-сжатие стержней
Построение эпюры N.

осевое растяжение-сжатие стержней
2. Подбор сечения: (1МПа =10-1 кН/см2)
Примем ( в запас прочности !)
А=13,4см2
Из условий прочности для опасных сечений стержня следует:

осевое растяжение-сжатие стержней
3. Определение