Слайд 4
ВВЕДЕНИЕ
Круг вопросов, изучаемых физикой чрезвычайно широк – от процессов, происходящих в микромире
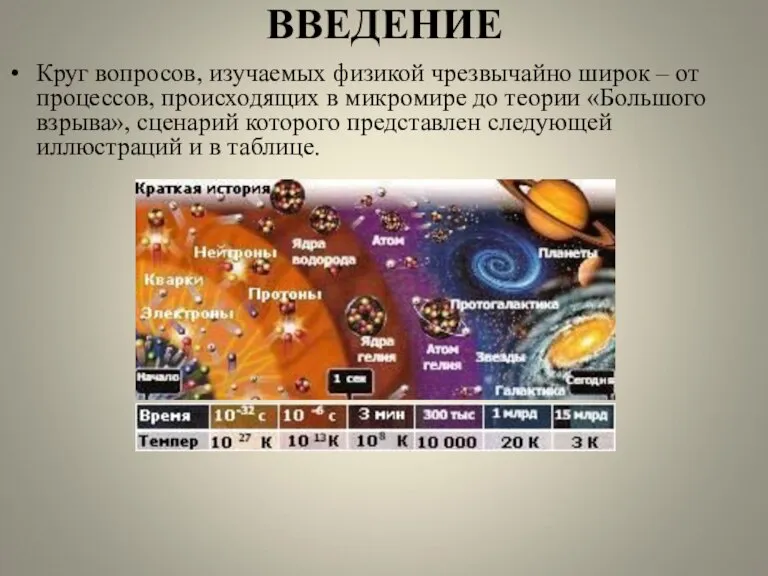
до теории «Большого взрыва», сценарий которого представлен следующей иллюстраций и в таблице.
Слайд 61922 — советский математик Ал. Ал. Фридман нашёл нестационарные решения гравитационного уравнения

Эйнштейна и предсказал расширение Вселенной в результате Большого взрыва.
1948 — выходит работа Г. А. Гамова о "горячей
вселенной", построенная на теории расширяющейся
после Большого взрыва вселенной Фридмана. Гамов
предположил, что первичное вещество было не только
очень плотным, но и очень горячим, в нем происходили
ядерные реакции, и за несколько минут были синтези-
рованы лёгкие химические элементы. Самым эффектным
результатом этой теории стало предсказание космического фона излучения. Электромагнитное излучение должно было, по законам термодинамики, существовать вместе с горячим веществом в "горячую" эпоху ранней Вселенной и сохраняется — только сильно охлаждённым — и до сих пор. В 1950 году Гамов эту температуру в 3 К. 1964 — американс-кие радиоастрономы А. Пензиас и Р. Вилсон открыли космический фон излучения и измерили его температуру: она оказалась равной 3 К!
Слайд 7
ВВЕДЕНИЕ
Достижения физики последних лет наглядно иллюстрируются следующими примерами.
Графен
Представьте себе углеродную пластину толщиной

всего в один атом, но более прочную, чем алмаз, и пропускающую электричество в 100 раз лучше, чем кремний компьютерных чипов. — Графен — самый тонкий и самый прочный материал во вселенной, — заявил 19 июня английский физик Андре Гейм (Andre Geim) из Университета Манчестера.
Слайд 8
ВВЕДЕНИЕ
За «передовые опыты с двумерным материалом графеном» А. К. ГеймуЗа «передовые опыты
с двумерным материалом графеном» А. К. Гейму и К. С. НовосёловуЗа «передовые опыты с двумерным материалом графеном» А. К. Гейму и К. С. Новосёлову была присуждена Нобелевская премияЗа «передовые опыты с двумерным материалом графеном» А. К. Гейму и К. С. Новосёлову была присуждена Нобелевская премия по физикеЗа «передовые опыты с двумерным материалом графеном» А. К. Гейму и К. С. Новосёлову была присуждена Нобелевская премия по физике за 2010 год
Слайд 9
ВВЕДЕНИЕ
105 лет с момента открытия сверхпроводимости.
В 1908 году нидерландский физик и химик

Хейке
Камерлинг-Оннес (1853 - 1926) впервые получил жидкий гелий и достиг рекордно низкой на тот момент температуры 0.9 K. В 1911 году он впервые
наблюдал резкое падение электрического сопротив-ления ртути при темперературе ниже 4.1 K. Это явление получило название сверхпроводимоcти. Нобелевская премия по физике 1913 г.
Большой адронный коллайдер. Сверхпроводящий магнит длиной 29 км
Слайд 12
I.Механика. Кинематика
Механика – раздел физики, изучающий простейшую форму движения материи

– механическую, т.е. изменение положения тела в пространстве и во времени. Обычная или классическая механика справедлива для малых скоростей << и макроскопических размеров. Для скоростей сравнимых со скоростью света используется механика СТО, а для микромира – квантовая механика, которые в пределе переходят в классическую механику. Механика делится на кинематику, динамику и статику.
Кинематика изучает движение тел без учета действия сил (причин его вызывающих).
Динамика изучает движение тел под действием сил.
Статика изучает равновесие тел под действием сил.
Кинематика материальной точки
Материальная точка – тело, размерами которого в данных условиях можно пренебречь. Двигаясь в пространстве тело описывает некоторую кривую, называемую траекторией. В зависимости от ее формы движение бывает прямолинейным, криволинейным, по окружности и т.д. Для описания движения используется радиус-вектор, соединяющий в данный момент точку на траектории с началом координат.
Слайд 13
I.Механика. Кинематика
Пусть в начальный момент времени t1 материальная точка

нахо-дится на траектории в положении 1, а в момент времени t2 – в положении 2 (рис.2). Путь – длина участка 12 вдоль траектории, пройденного телом за рассматриваемый промежуток времени. – неубывающая положительная скалярная величина. Перемещением называется вектор, соединяющий точки 1 и 2 траектории:
Слайд 14I.Механика. Кинематика
Для характеристики движения вводится средняя скорость на участке 12

Слайд 15
I.Механика. Кинематика
При неравномерном движении средняя скорость постоянно меня-ется, поэтому вводят

мгновенную скорость или просто скорость. Она определяется как предел средней скорости при
При модуль перемещения стремится к соответст-вующей длине пути, поэтому модуль или величина скорости
.
Обратное соотношение имеет вид .
Слайд 16I.Механика. Кинематика
Скорость в данной точке направлена по касательной к траектории
,
где - единичный

вектор, определяющий направление касательной в данной точке траектории.
Для определения пройденного пути на конечном участке 12 траекто-рии его необходимо разбить на отрезки
В пределе при получим .
Слайд 17
I.Механика. Кинематика
Ускорение – быстрота изменения скорости. Среднее значение ус-
корения

равно ,
а мгновенное ускорение или просто ускорение
Обратное соотношение имеет вид
Используя связь между и , можно получить закон движения
или x(t), y(t), z(t). При равнопеременном движении с
постоянным ускорением ax вдоль оси x получим:
Слайд 18
I.Механика. Кинематика
, где – начальная скорость, а .
Для

координаты x получим:
или
.
Найдем путь, пройденный телом, движущимся из начала координат с постоянным ускорением ax, если его скорость возросла от до . Выразим t из соотношения между скоростью и ускорением и
подставим его в выражение для перемещения вдоль оси x. Полученная формула полезна при решении ряда задач.
Слайд 19
I.Механика. Кинематика
Ускорение при криволинейном движении
В общем случае криволинейного движения материальной

точки ускорение равно
- единичный вектор, поэтому . Продифференцируем
это равенство . Каждый из векторов и отличен от
нуля, поэтому угол между ними равен 90°, перпендикулярен
вектору и направлен по нормали к касательной в данной точке.
Модуль этого вектора равен ,
т.е. И , где - единичный вектор
нормали.
Слайд 20
I.Механика. Кинематика
Окончательно, получим . Первое слагаемое –
тангенциальное ускорение
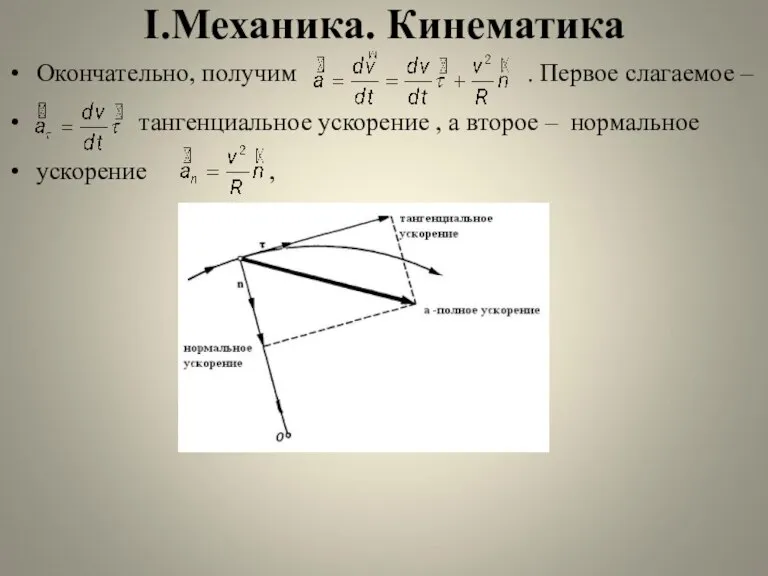
, а второе – нормальное
ускорение ,



















 Количество теплоты. Единицы количества теплоты. Удельная теплоемкость
Количество теплоты. Единицы количества теплоты. Удельная теплоемкость Тест. 8 класс
Тест. 8 класс Презентация по физике "Техника безопасности в кабинете физики" -
Презентация по физике "Техника безопасности в кабинете физики" -  Магнитное поле Земли
Магнитное поле Земли Свойство волн
Свойство волн Процессы теплопередачи. Сложный теплообмен и теплопередача
Процессы теплопередачи. Сложный теплообмен и теплопередача Теория движения военных колесных машин. Лекция 3
Теория движения военных колесных машин. Лекция 3 Сенсори температури охолоджувальної рідини
Сенсори температури охолоджувальної рідини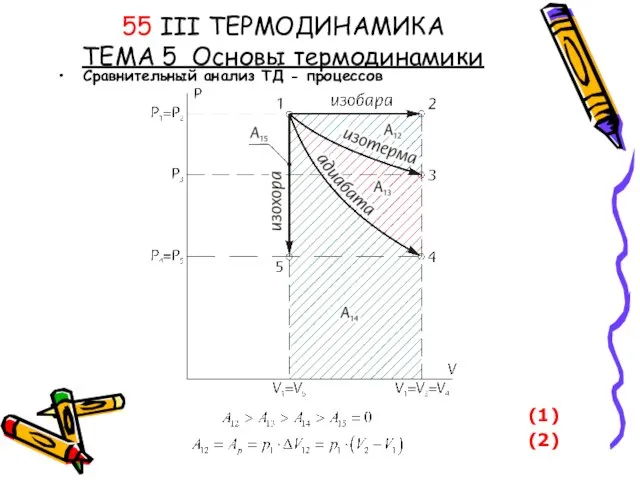 55 III ТЕРМОДИНАМИКА ТЕМА 5 Основы термодинамики Сравнительный анализ ТД - процессов
55 III ТЕРМОДИНАМИКА ТЕМА 5 Основы термодинамики Сравнительный анализ ТД - процессов Расчет свободной энергии с помощью молекулярной динамики
Расчет свободной энергии с помощью молекулярной динамики Метод перемещений расчета на устойчивост.ь Пример расчета
Метод перемещений расчета на устойчивост.ь Пример расчета История создания швейной машины
История создания швейной машины Презентация на тему Постоянные магниты. Магнитное поле Земли
Презентация на тему Постоянные магниты. Магнитное поле Земли 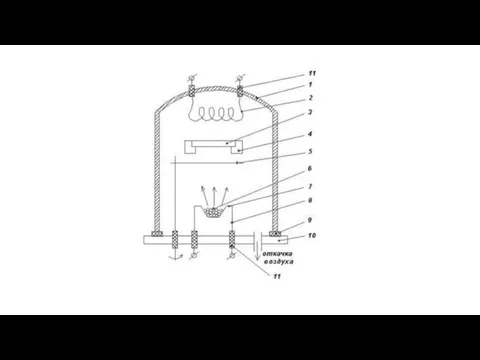 Физико-химические основы термического вакуумного напыления тонких пленок. Тема 8
Физико-химические основы термического вакуумного напыления тонких пленок. Тема 8 Регулирование гидромуфт
Регулирование гидромуфт Марковские процессы
Марковские процессы Safarov_Krasnov
Safarov_Krasnov Метод проектов на уроках физики
Метод проектов на уроках физики Физика в медицине. Элективный курс предпрофильной подготовки обучающихся 9-х классов
Физика в медицине. Элективный курс предпрофильной подготовки обучающихся 9-х классов Плазмохімічне одержання сполук заліза. Магістерська робота
Плазмохімічне одержання сполук заліза. Магістерська робота Магнитный поток
Магнитный поток Шаговое напряжение
Шаговое напряжение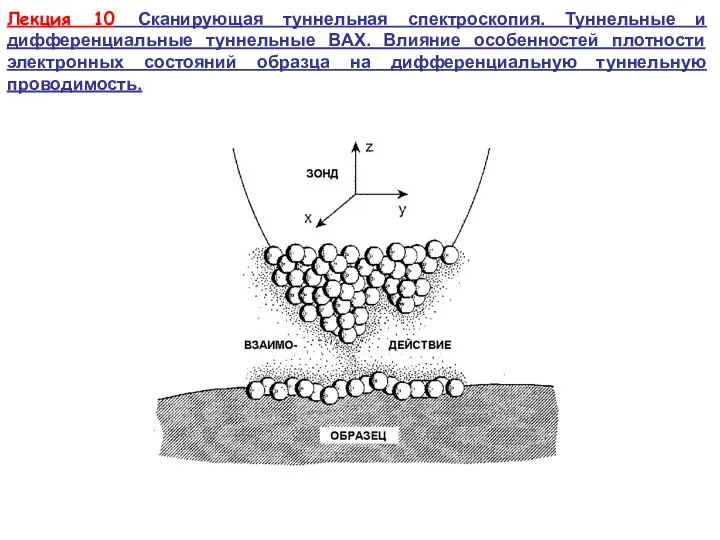 Сканирующая туннельная спектроскопия. Туннельные и дифференциальные туннельные ВАХ
Сканирующая туннельная спектроскопия. Туннельные и дифференциальные туннельные ВАХ Радиоактивность. Человек и радиация
Радиоактивность. Человек и радиация Идентификация и моделирование CW–crds спектра поглощения молекулы двуокиси азота в области 6000 – 6400 см -1
Идентификация и моделирование CW–crds спектра поглощения молекулы двуокиси азота в области 6000 – 6400 см -1 Роль домашнего демонстрационного физического эксперимента в формировании интереса школьников к урокам физики
Роль домашнего демонстрационного физического эксперимента в формировании интереса школьников к урокам физики Тепловое действие электрического тока. Закон Джоуля-Ленца
Тепловое действие электрического тока. Закон Джоуля-Ленца Момент силы относительно точки
Момент силы относительно точки