Содержание
- 2. Дифракция света – это совокупность явлений, наблюдаемых при распространении света сквозь малые отверстия или вблизи границ
- 3. Особенности физической природы интерференции и дифракции интерференцией волн принято называть перераспределение интенсивности, возникающее в результате суперпозиции
- 4. Поэтому говорят, например, об интерференционной картине от двух узких щелей и о дифракционной картине от одной
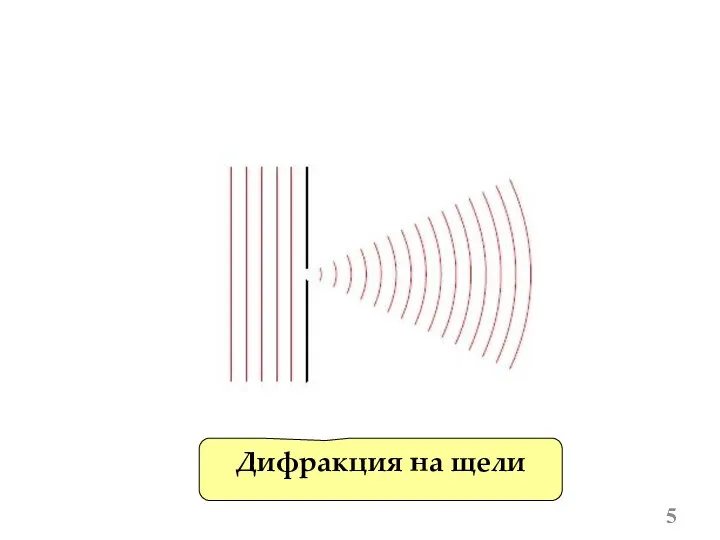
- 5. Дифракция на щели
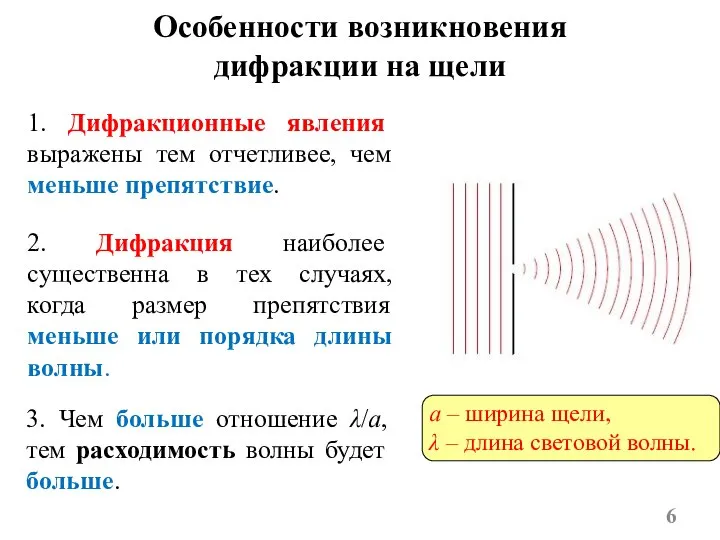
- 6. Особенности возникновения дифракции на щели 1. Дифракционные явления выражены тем отчетливее, чем меньше препятствие. 3. Чем
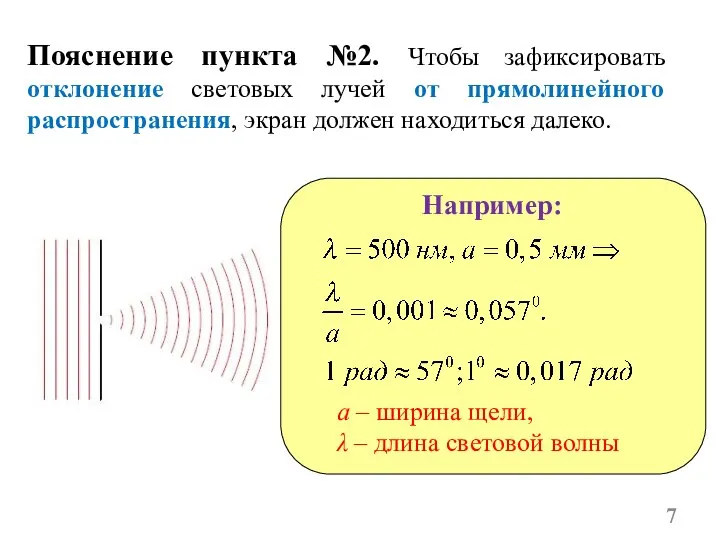
- 7. Пояснение пункта №2. Чтобы зафиксировать отклонение световых лучей от прямолинейного распространения, экран должен находиться далеко. Например:
- 8. Что мы наблюдаем? Мы наблюдаем дифракционную картину, представляющую собой чередующиеся светлые и темные кольца, которые являются
- 9. Принцип Гюйгенса Каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн
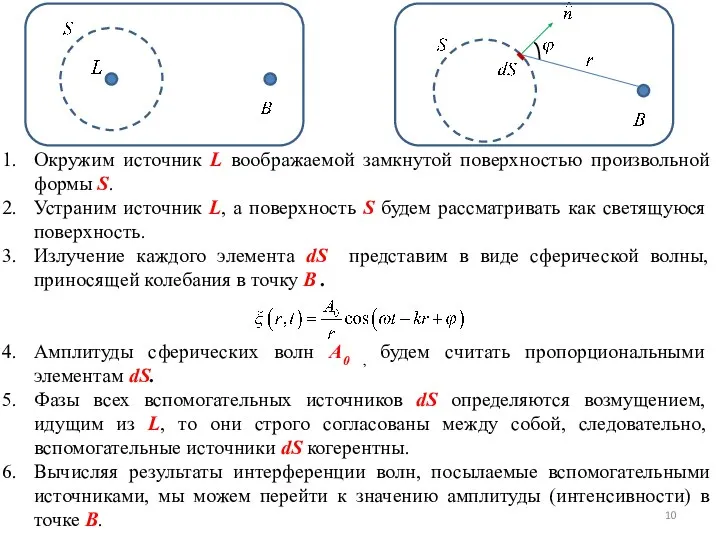
- 10. Окружим источник L воображаемой замкнутой поверхностью произвольной формы S. Устраним источник L, а поверхность S будем
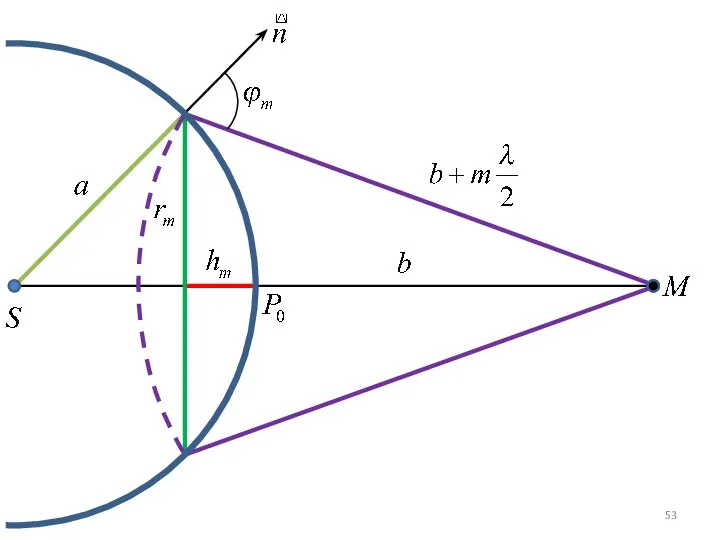
- 11. Метод Зон Френеля Рассмотрим действие световой волны из точки S (источник) в какой-либо точке наблюдения M.
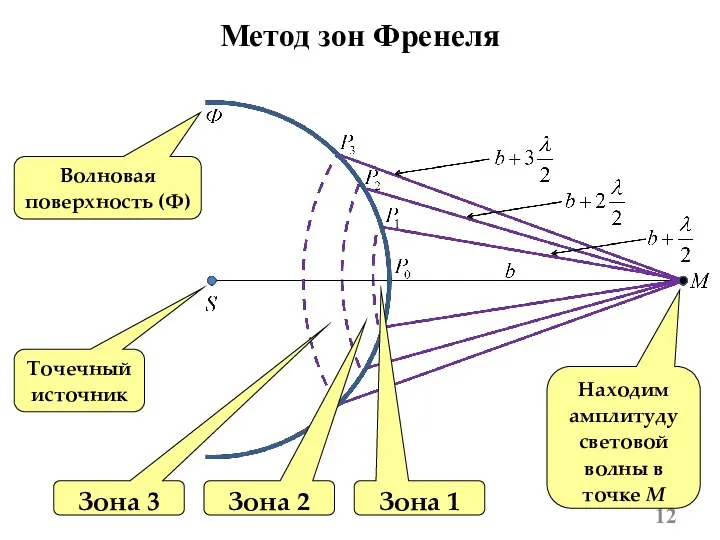
- 12. Метод зон Френеля Зона 1 Зона 2 Зона 3 Точечный источник Находим амплитуду световой волны в
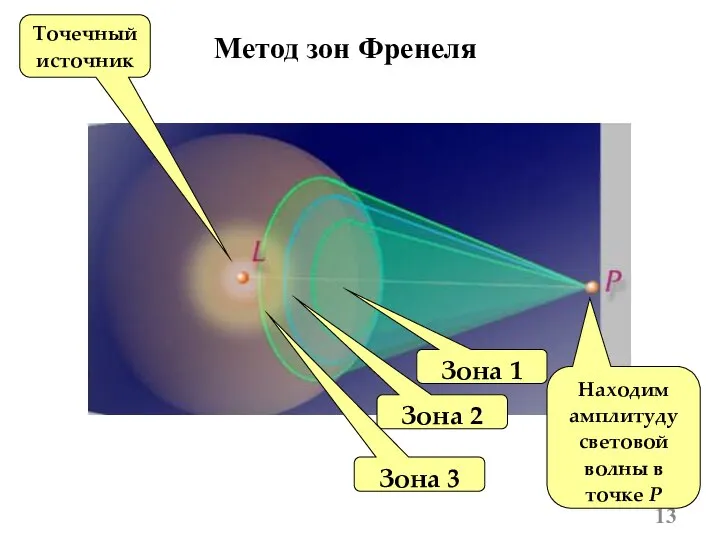
- 13. Метод зон Френеля Зона 1 Зона 2 Зона 3 Точечный источник Находим амплитуду световой волны в
- 14. Так как колебания от соседних зон проходят до точки M расстояния, отличающиеся на λ/2, то в
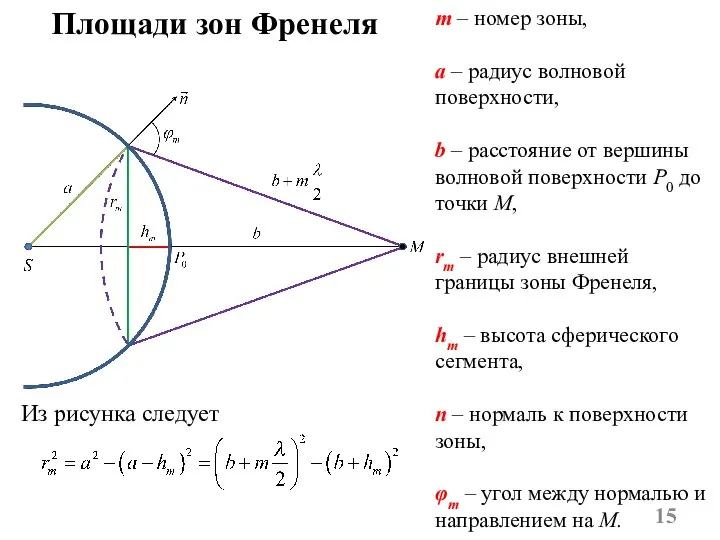
- 15. Площади зон Френеля m – номер зоны, a – радиус волновой поверхности, b – расстояние от
- 16. Площадь сферического сегмента σm m-й зоны Френеля равны Выражение не зависит от m, следовательно, при не
- 17. Действие зон постепенно убывает от центральной к периферическим (с ростом m): Общее число зон Френеля, умещающихся
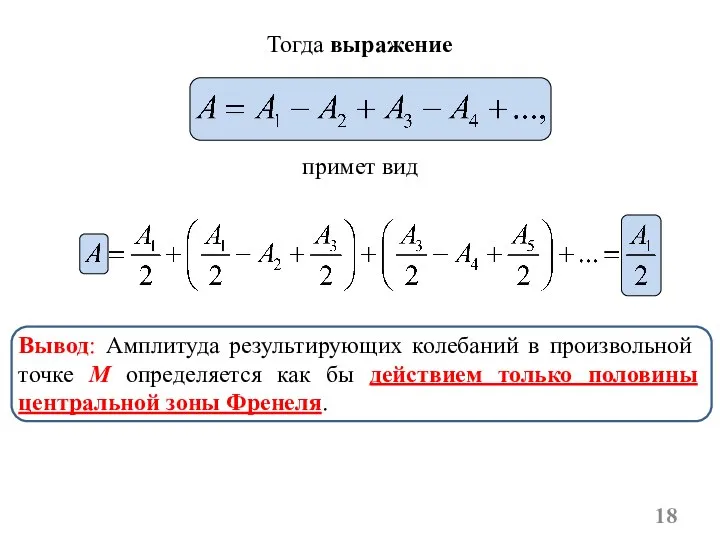
- 18. Тогда выражение примет вид Вывод: Амплитуда результирующих колебаний в произвольной точке M определяется как бы действием
- 19. Подставив сюда выражение , найдем радиус внешней границы m-й зоны Френеля: a=b=10 см, λ=0,5 мкм r1=0,158
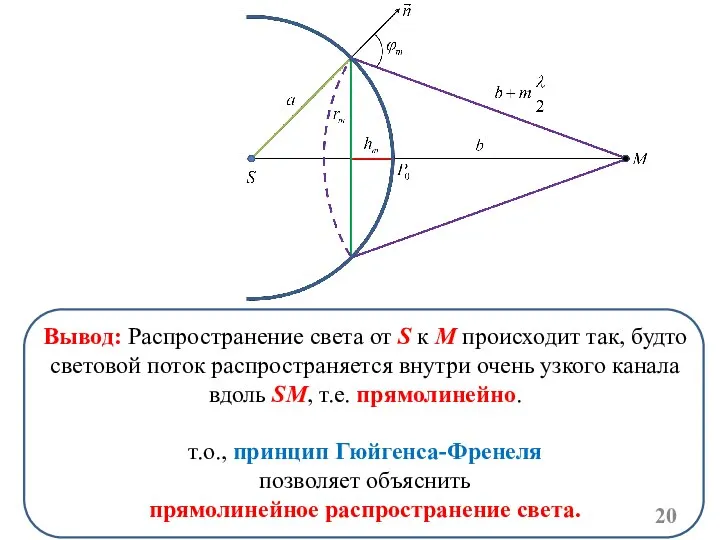
- 20. Вывод: Распространение света от S к M происходит так, будто световой поток распространяется внутри очень узкого
- 21. Это стеклянные пластинки, состоящие из системы чередующихся прозрачных и непрозрачных концентрических колец, построенных по принципу расположения
- 22. I. Дифракция Френеля (дифракция в сходящихся лучах) В этом случае на препятствие падает сферическая или плоская
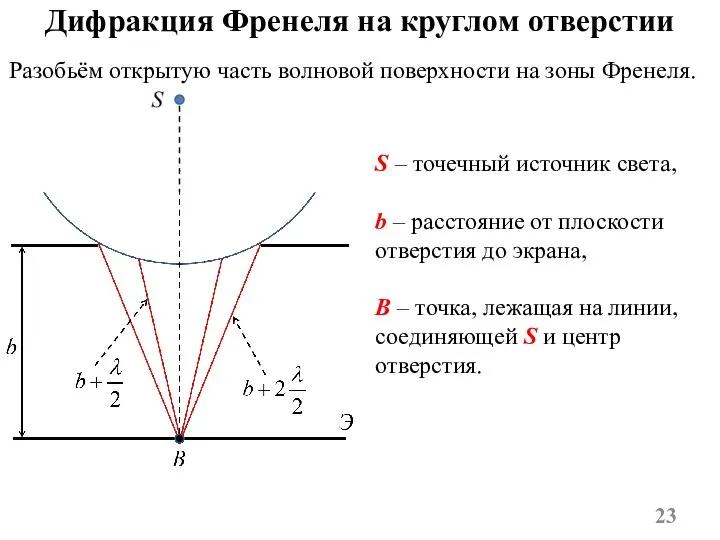
- 23. Дифракция Френеля на круглом отверстии S – точечный источник света, b – расстояние от плоскости отверстия
- 24. Если отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке B будет больше, чем
- 25. Если отверстие открывает одну зону Френеля, то амплитуда в точке B будет равна A1, т.е. вдвое
- 26. Дифракционная картина от круглого отверстия вблизи точки B будет иметь вид чередующихся темных и светлых колец
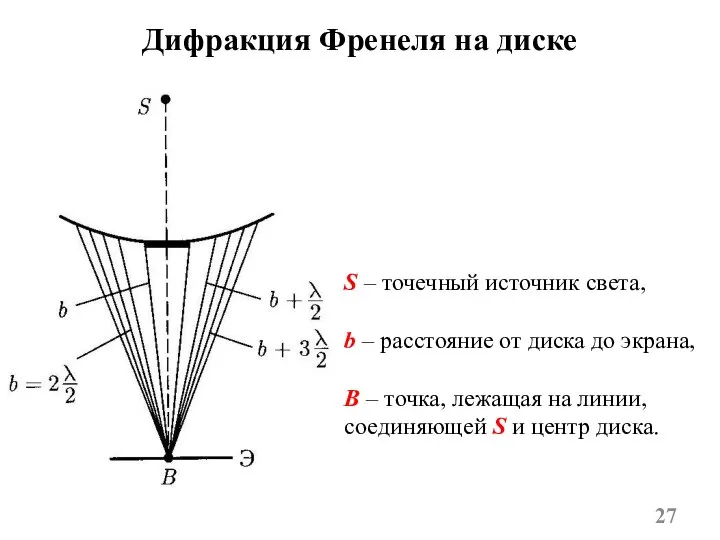
- 27. Дифракция Френеля на диске S – точечный источник света, b – расстояние от диска до экрана,
- 28. Внимание! Закрытый диском участок волнового фронта надо исключить из рассмотрения и строить зоны Френеля, начиная с
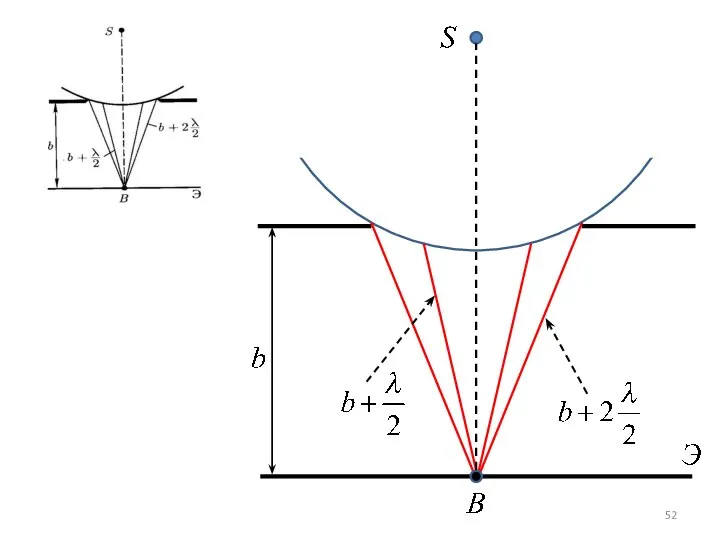
- 29. В точке B всегда наблюдается интерференционный максимум (светлое пятно Пуассона), соответствующий половине действия первой открытой зоны
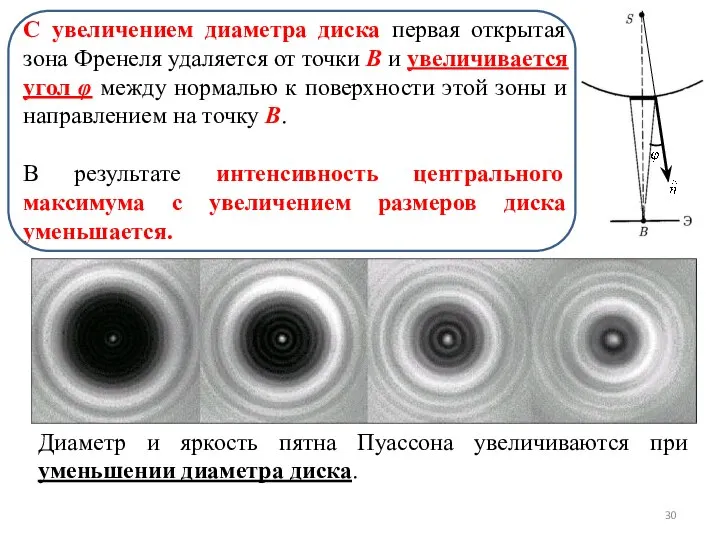
- 30. С увеличением диаметра диска первая открытая зона Френеля удаляется от точки B и увеличивается угол φ
- 31. Наблюдается в том случае, когда источник света и точка наблюдения бесконечны удалены от препятствия, вызвавшего дифракцию.
- 32. Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной a. Согласно принципу Гюйгенса –
- 33. Оптическая разность хода ΔL между крайними лучами MC и PD, идущими от щели в произвольном направлении
- 34. Если число зон Френеля чётное, то В точке B наблюдается дифракционный минимум (полная темнота) Если число
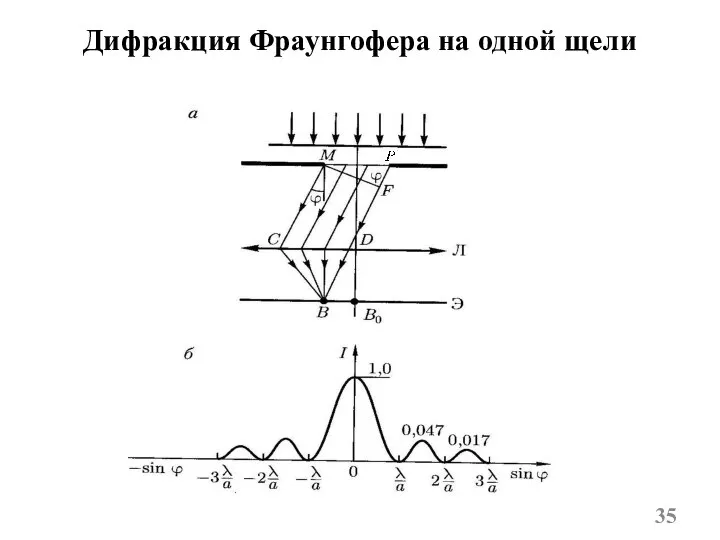
- 35. Дифракция Фраунгофера на одной щели
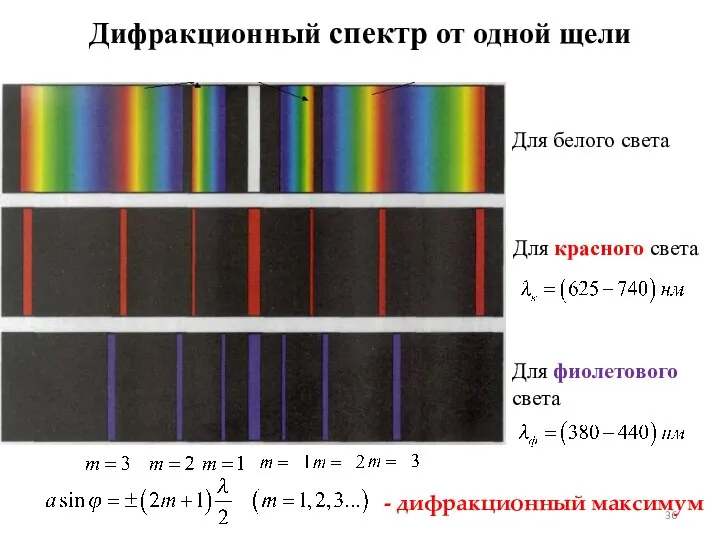
- 36. Дифракционный спектр от одной щели Для белого света Для красного света Для фиолетового света - дифракционный
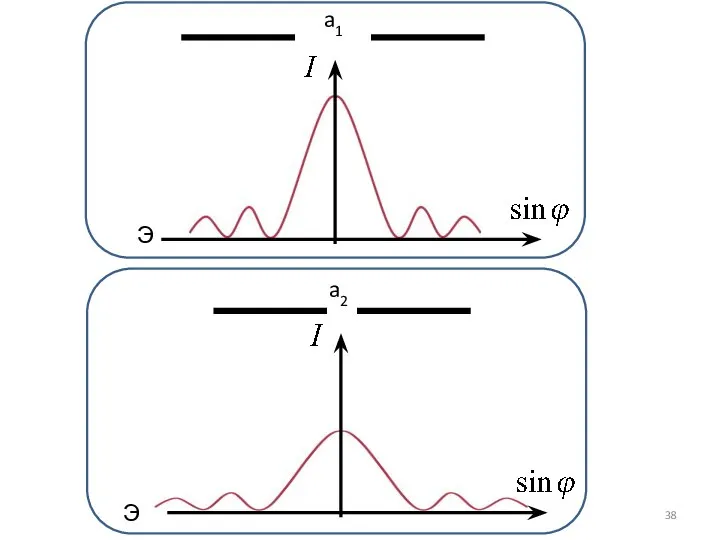
- 37. 1. Из формулы для дифракционного минимума следует, что с уменьшением ширины щели a центральная светлая полоса
- 39. При освещении щели белым светом центральный максимум наблюдается в виде белой полоски, переходящей в цветную каёмку.
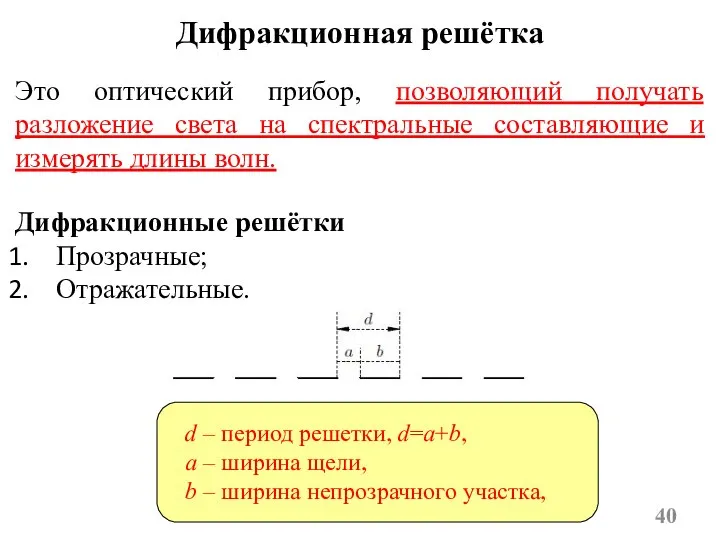
- 40. Дифракционная решётка Это оптический прибор, позволяющий получать разложение света на спектральные составляющие и измерять длины волн.
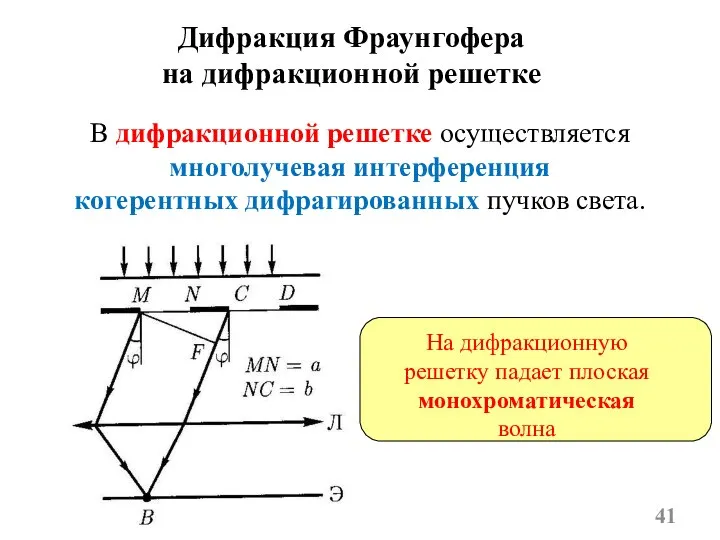
- 41. Дифракция Фраунгофера на дифракционной решетке В дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света. На
- 42. Т.к. щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух
- 43. Но в дифракционной решетке возникнут дополнительные минимумы, так как вследствие взаимной интерференции световых лучей, посылаемых двумя
- 44. Наоборот, действие одной щели будет усиливать действие другой, если Это условие главных максимумов. Максимумов нулевого порядка
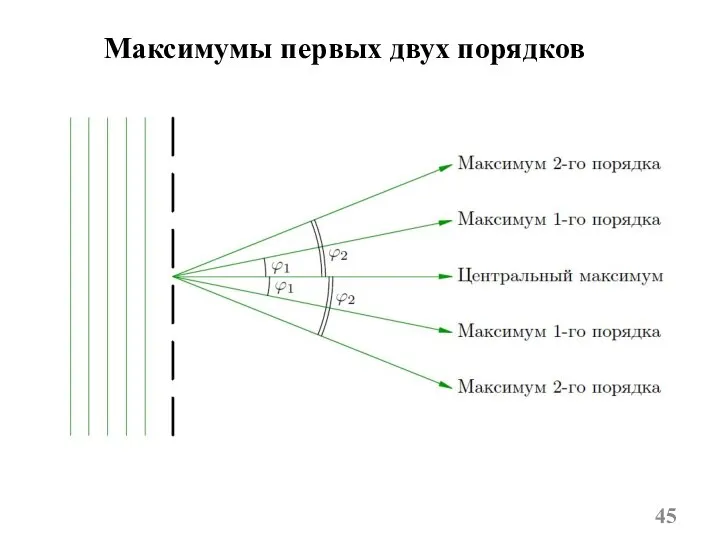
- 45. Максимумы первых двух порядков
- 46. Дифракционный спектр — равномерный во всех областях и располагается в порядке возрастания длин волн: от фиолетового
- 47. перья птиц; крылья бабочек; перламутровая поверхность морской раковины; компакт-диск (дорожки на поверхности диска образуют отражательную дифракционную
- 48. Дифракция лазерного луча на дифракционной решетке
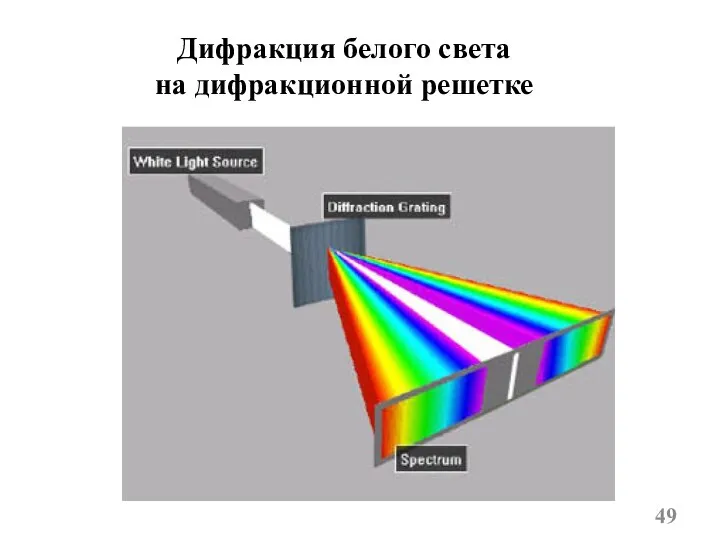
- 49. Дифракция белого света на дифракционной решетке
- 50. Дифракция на компакт-диске (отражательная дифракционная решетка)
- 51. Почему свет распространяется только в одну сторону? Вторичные волны, интерферируя, усиливают друг друга на огибающей своих
- 55. Скачать презентацию































 Явление тяготения. Сила тяжести
Явление тяготения. Сила тяжести Тест
Тест Оптика, квантовая оптика, квантовая механика
Оптика, квантовая оптика, квантовая механика Сила
Сила Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Электрический ток в жидкостях
Электрический ток в жидкостях Отсчёт по производственной практике
Отсчёт по производственной практике 2_kurs_lektsia_1_2
2_kurs_lektsia_1_2 Решение задач по кинематики
Решение задач по кинематики Проводники и диэлектрики
Проводники и диэлектрики В мире звуков
В мире звуков 实验五 功率放大电路
实验五 功率放大电路 Презентация на тему Изобретение радио Поповым (11 класс)
Презентация на тему Изобретение радио Поповым (11 класс)  Технология проверки технического состояния направляющих и ведущих колёс
Технология проверки технического состояния направляющих и ведущих колёс Решение многоуровневой задачи. Эйфелева башня
Решение многоуровневой задачи. Эйфелева башня Презентация на тему Деление ядер урана
Презентация на тему Деление ядер урана  Электростатика. Основы электромеханики
Электростатика. Основы электромеханики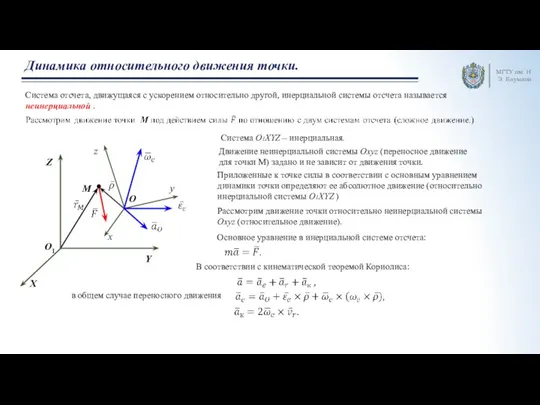 Динамика относительного движения точки. Лекция 2
Динамика относительного движения точки. Лекция 2 f3c279363c6051c6009ac4b1a3800ded
f3c279363c6051c6009ac4b1a3800ded Техническая механика
Техническая механика Квантовый протокол E91. Неравенства Белла
Квантовый протокол E91. Неравенства Белла Электромагнитная природа света
Электромагнитная природа света Сила трения
Сила трения Изобретение радио
Изобретение радио Искусственный интеллект. Сценарий №1
Искусственный интеллект. Сценарий №1 Плоская система сходящихся сил. Определение равнодействующей аналитическим способом
Плоская система сходящихся сил. Определение равнодействующей аналитическим способом Генератор 2ГВ-008
Генератор 2ГВ-008 Определение реакций связей твердого тела
Определение реакций связей твердого тела