Основы гидродинамического подобия. Лекция №5

ПЛАН ЛЕКЦИИ
1. Режимы движения жидкости (ламинарный и турбулентный). Числа и критерии гидродинамического подобия. Моделирование гидродинамических явлений.
2. Понятие о методе размерностей. Пи-теорема. Применение методов теории размерностей к исследованию гидравлических закономерностей.
3. Гидравлические сопротивления, их физическая природа и классификация. Структура формул для вычисления потерь энергии (напора).

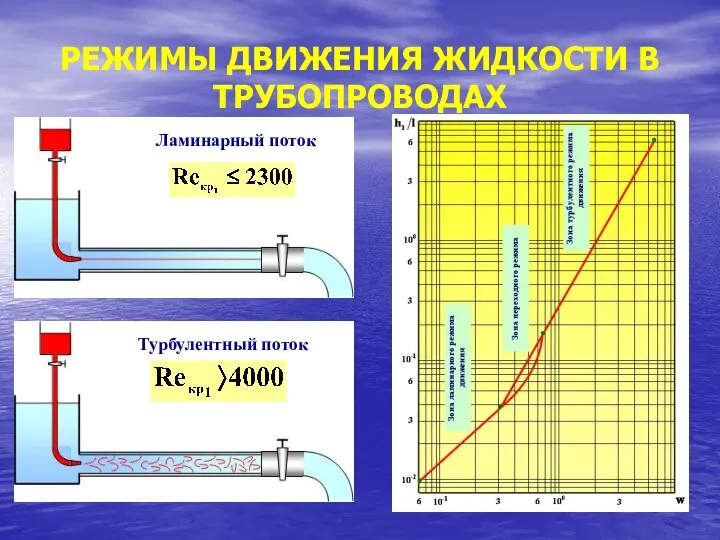
РЕЖИМЫ ДВИЖЕНИЯ
РЕАЛЬНОЙ ЖИДКОСТИ
В природе существует два режима движения жидкости.
Ламинарный (слоистый) режим движения, при котором частицы жидкости в потоке движутся упорядоченно в виде несмешивающихся струек или слоев.
Турбулентный, при котором частицы жидкости имеют сложные неупорядоченные траектории движения, вследствие чего происходит интенсивное перемешивание потока.

РЕЖИМЫ ДВИЖЕНИЯ
РЕАЛЬНОЙ ЖИДКОСТИ
1869 год немецкий ученый Хаген отметил, что закон сопротивления движению жидкости зависит от режима движения.
1880 год русский ученый Менделеев в своем сочинении «О сопротивлении жидкости и о воздухоплавании» указал на существование в природе двух режимов движения жидкости с разным законом ее сопротивления.
1883 год русский физик Петров установил, что при смазке силы трения, определяемые вязким сопротивлением, при ламинарном режиме, пропорциональны первой степени скорости.

РЕЖИМЫ ДВИЖЕНИЯ
РЕАЛЬНОЙ ЖИДКОСТИ
Наиболее полные исследования жидкости в трубах были проведены английским физиком Рейнольдсом (1881-1883 г.), который предложил установку для экспериментального определения режима движения жидкости.
Рейнольдс установил, что границы ламинарного и турбулентного режима движения жидкости необходимо определять не постоянной величиной скорости потока, а постоянной величиной числа Рейнольдса.

РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ В ТРУБОПРОВОДАХ
Ламинарный поток

ОСНОВЫ ТЕОРИИ ПОДОБИЯ
Законы сочетания аналитических и экспериментальных исследований в значительной степени определяет теория подобия – наука о правильной организации и проведении эксперимента и теория размерностей.

ОСНОВЫ ТЕОРИИ ПОДОБИЯ
Теория подобия дает ответ:
какие условия необходимы и достаточны для существования подобия двух или более систем;
какие физические величины необходимо измерять в процессе исследования, как обрабатывать результаты исследований, чтобы их можно было распространить на все подобные процессы и явления.

УСЛОВИЯ И МАСШТАБЫ
ПОДОБИЯ
Геометрическое подобие – равенство соответствующих углов и пропорциональность сходственных линейных размеров, площадей и объемов
Линейный масштаб подобия

УСЛОВИЯ И МАСШТАБЫ
ПОДОБИЯ
Кинематическое подобие – пропорциональность местных скоростей в сходственных точках и равенство углов,
характеризующих направление этих скоростей
Масштаб времени
Масштаб скорости

УСЛОВИЯ И МАСШТАБЫ
ПОДОБИЯ
Динамическое подобие – пропорциональность сил, действующих на сходственные объемы в кинематически подобных потоках и равенство углов, характеризующих направление этих сил
Масштаб плотности
Масштаб сил

КРИТЕРИИ ПОДОБИЯ
Критерий Ньютона

КРИТЕРИИ ПОДОБИЯ
Доминирующая сила – сила вязкого сопротивления
Критерий Рейнольдса
Критерий Рейнольдса – величина пропорциональная отношению сил инерции к силам трения

КРИТЕРИИ ПОДОБИЯ
Доминирующая сила – сила давления
Критерий Эйлера
Критерий Эйлера – величина пропорциональная отношению сил давления к силам инерции

КРИТЕРИИ ПОДОБИЯ
Доминирующая сила – сила тяжести
Критерий Фруда
Критерий Фруда – величина пропорциональная отношению сил инерции к силам тяжести

ПРИМЕНЕНИЕ МЕТОДА
АНАЛИЗА РАЗМЕРНОСТЕЙ
При различных гидравлических исследованиях приходиться устанавливать функциональные зависимости между физическими величинами, оказывающими влияние на исследуемые явления, которые могут быть получены из анализа размерностей. В основе этого метода лежит так называемая Пи-теорема, или теорема Бэкингема, основанная на том, что функциональная зависимость между «n» физическими размерными величинами всегда может быть преобразована в уравнение, содержащее «m» безразмерных комбинаций тех же физических величин (так называемых чисел ).

ПРИМЕНЕНИЕ МЕТОДА
АНАЛИЗА РАЗМЕРНОСТЕЙ
Равенство безразмерных величин в подобных потоках выражает равенство относительных значений соответствующих физических величин, поэтому эти величины могут представлять собой соответствующие критерии подобия.
При гидравлических исследованиях оказывается целесообразным из числа переменных выбрать следующие три величины с независимыми размерностями, включающими в себя три основных единицы (длины, времени и массы):
характерный линейный размер, как правило, для труб круглого сечения это диаметр трубопровода – = м;
средняя скорость потока – = м⋅с-1;
плотность жидкости – = кг⋅м-3.

ПРИМЕНЕНИЕ МЕТОДА
АНАЛИЗА РАЗМЕРНОСТЕЙ
Через основные величины можно выразить размерность любой величины, входящей в функциональные зависимости
Численные значения
Значения отвлеченных чисел

ПРИМЕНЕНИЕ МЕТОДА
АНАЛИЗА РАЗМЕРНОСТЕЙ
Показатели степеней находят из условия безразмерности числа , т.е. путем сравнения размерностей левой и правой частей при первичных единицах – метр, секунда и килограмм.

ПРИМЕНЕНИЕ МЕТОДА
АНАЛИЗА РАЗМЕРНОСТЕЙ
Свойства теоремы
Если в числителе и знаменателе содержаться величины с одинаковой размерностью, то число представляет собой отношение этих величин.
Если в числителе и знаменателе имеются одинаковые величины, то число равно единице ( ).

ПРИМЕНЕНИЕ МЕТОДА
АНАЛИЗА РАЗМЕРНОСТЕЙ

ПРИМЕНЕНИЕ МЕТОДА
АНАЛИЗА РАЗМЕРНОСТЕЙ
симплекс геометрического подобия
относительная шероховатость
Показатели степени
При кг:
При м:
При с:

ПРИМЕНЕНИЕ МЕТОДА
АНАЛИЗА РАЗМЕРНОСТЕЙ