Основы медицинской и биологической физики. Лекция 4. Часть 1

Лекция 3
ОСНОВЫ МЕДИЦИНСКОЙ и БИОЛОГИЧЕСКОЙ ФИЗИКИ
Часть I

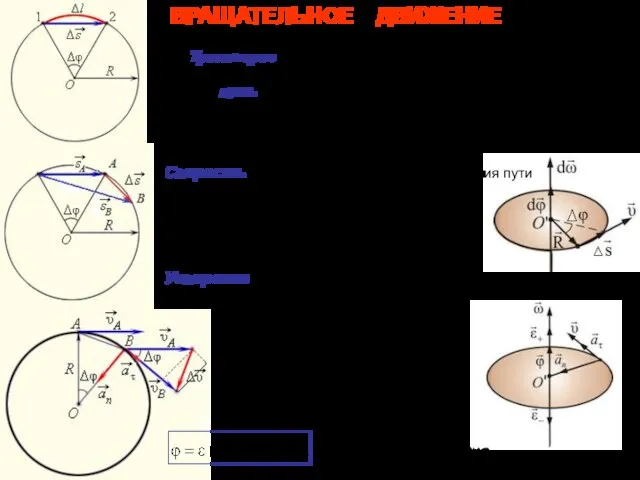
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Δs - перемещение
Δl ≈ Δs
Δφ – угловое перемещение
при Δφ → 0 Δt → 0
Траектория – линия по которой движется тело
Δt - время движения
Δl – путь – длина траектории
Ускорение – характеризует быстроту изменения скорости
Скорость – характеризует быстроту изменения пути
- уравнение движения

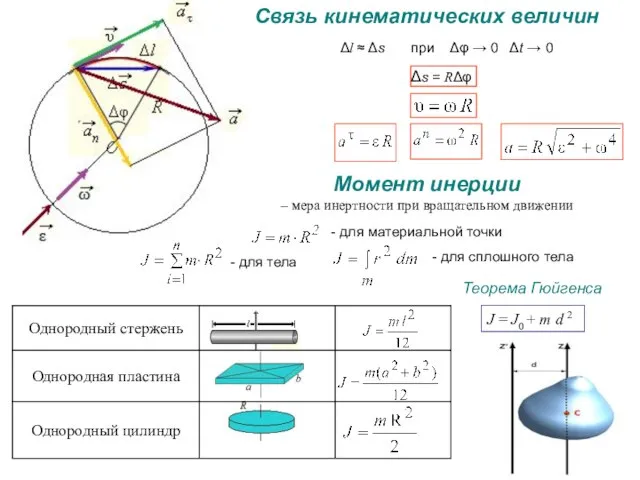
Связь кинематических величин
Δs = RΔφ
при Δφ → 0 Δt → 0
Δl ≈ Δs
Момент инерции
– мера инертности при вращательном движении
- для материальной точки
- для тела
- для сплошного тела
Теорема Гюйгенса
J = J0 + m d 2

Динамика вращательного движения

Центрифугирование

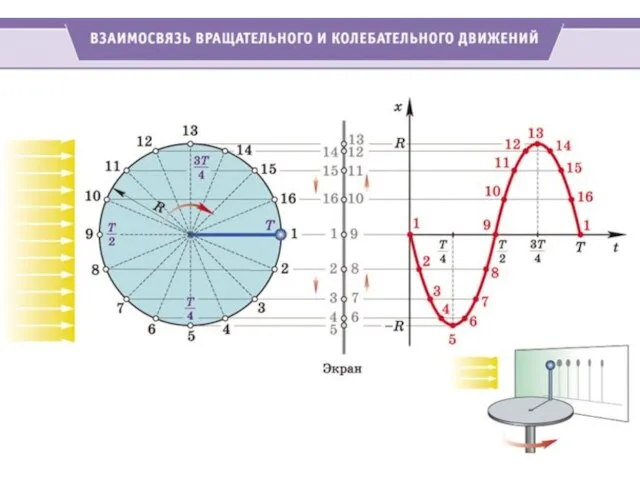
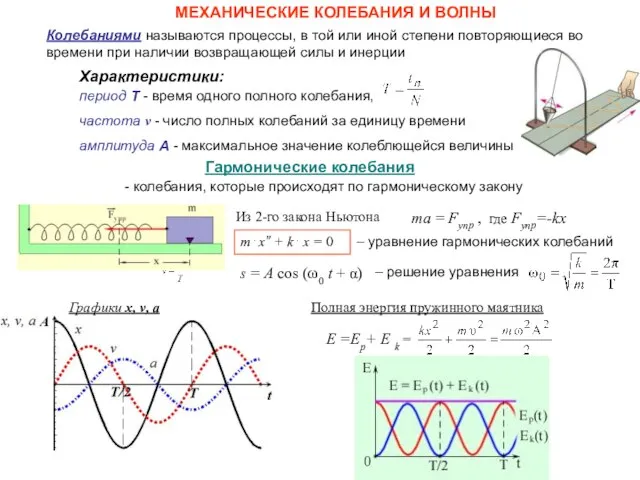
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
Гармонические колебания
Колебаниями называются процессы, в той или иной степени повторяющиеся во времени при наличии возвращающей силы и инерции
Характеристики:
период Т - время одного полного колебания,
частота ν - число полных колебаний за единицу времени
амплитуда А - максимальное значение колеблющейся величины
- колебания, которые происходят по гармоническому закону
ma = Fупр , где Fупр=-kx
Из 2-го закона Ньютона
m . x” + k . x = 0
– уравнение гармонических колебаний
s = A cos (ω0 t + α)
– решение уравнения
Графики x, v, a
Полная энергия пружинного маятника
E =Ep+ E k =

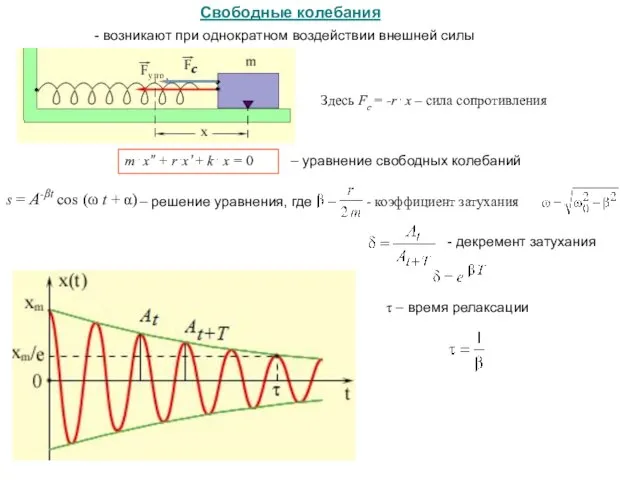
Свободные колебания
- возникают при однократном воздействии внешней силы
– уравнение свободных колебаний
s = A-βt cos (ω t + α)
– решение уравнения, где
m . x” + r .x’ + k . x = 0
Здесь Fc = -r , x – сила сопротивления
- коэффициент затухания
- декремент затухания
τ – время релаксации

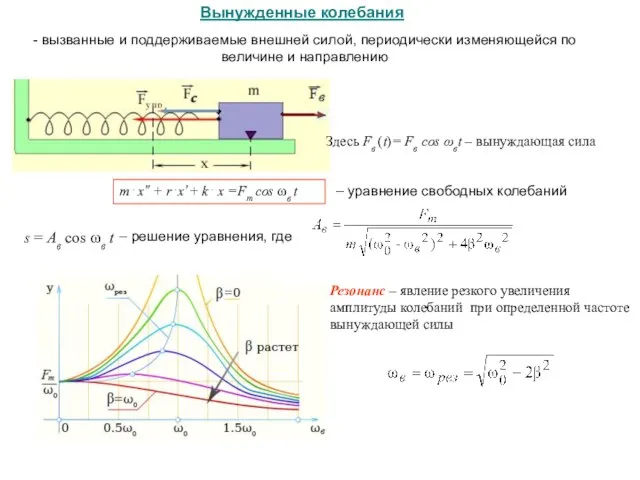
Вынужденные колебания
- вызванные и поддерживаемые внешней силой, периодически изменяющейся по величине и направлению
m . x” + r .x’ + k . x =Fm cos ωв t
– уравнение свободных колебаний
Здесь Fв (t)= Fв cos ωвt – вынуждающая сила
s = Aв cos ωв t
– решение уравнения, где
Резонанс – явление резкого увеличения амплитуды колебаний при определенной частоте вынуждающей силы

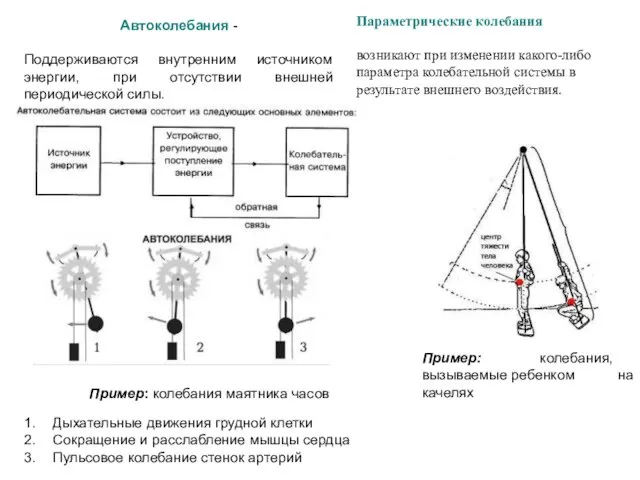
Параметрические колебания
возникают при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.
Автоколебания -
Поддерживаются внутренним источником энергии, при отсутствии внешней периодической силы.
Пример: колебания, вызываемые ребенком на качелях
Пример: колебания маятника часов
Дыхательные движения грудной клетки
Сокращение и расслабление мышцы сердца
Пульсовое колебание стенок артерий

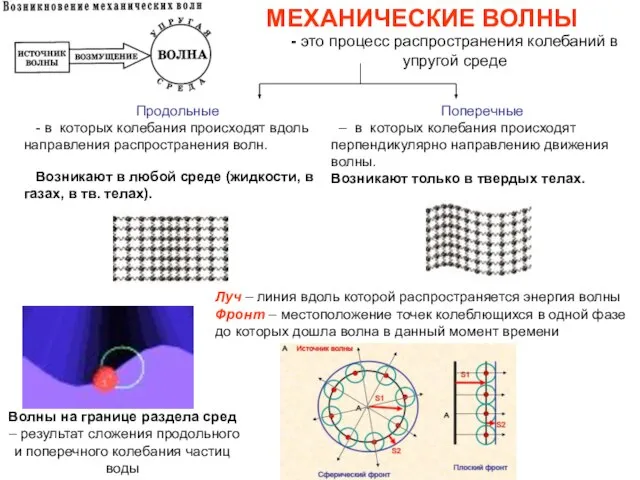
МЕХАНИЧЕСКИЕ ВОЛНЫ
- это процесс распространения колебаний в упругой среде
Поперечные
– в которых колебания происходят перпендикулярно направлению движения волны.
Возникают только в твердых телах.
Продольные
- в которых колебания происходят вдоль направления распространения волн.
Возникают в любой среде (жидкости, в газах, в тв. телах).
Волны на границе раздела сред – результат сложения продольного и поперечного колебания частиц воды
Луч – линия вдоль которой распространяется энергия волны
Фронт – местоположение точек колеблющихся в одной фазе до которых дошла волна в данный момент времени

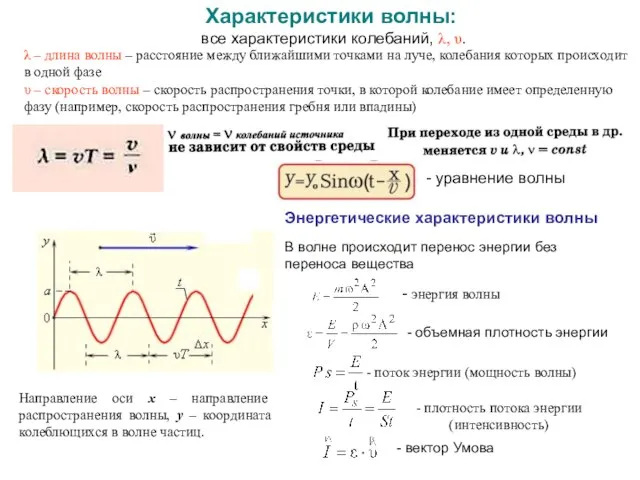
Характеристики волны:
все характеристики колебаний, λ, υ.
λ – длина волны – расстояние между ближайшими точками на луче, колебания которых происходит в одной фазе
υ – скорость волны – скорость распространения точки, в которой колебание имеет определенную фазу (например, скорость распространения гребня или впадины)
Направление оси х – направление распространения волны, у – координата колеблющихся в волне частиц.
- уравнение волны
Энергетические характеристики волны
В волне происходит перенос энергии без переноса вещества
- энергия волны
- объемная плотность энергии
- поток энергии (мощность волны)
- плотность потока энергии (интенсивность)
- вектор Умова

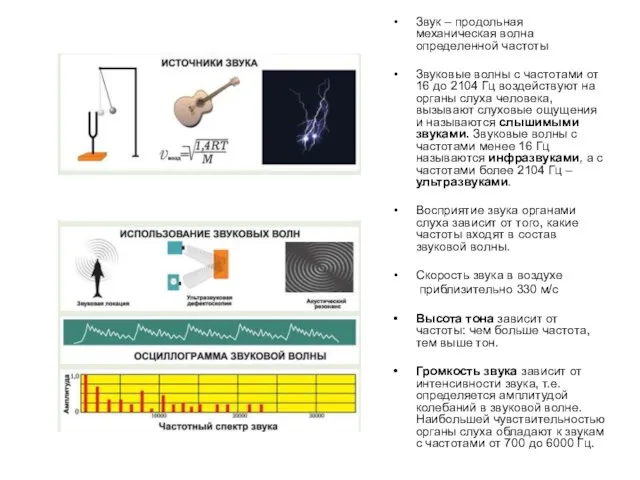
АКУСТИКА
Звук - колебания частиц в упругих средах, распространяющиеся в форме продольных волн, частота которых лежит в пределах, воспринимаемых человеческим ухом, в среднем от 16 до 20000 Гц, называются звуковыми колебаниями или просто звуком.
Виды звука:
Тон – звук, являющийся периодическим процессом.
Шум – звук, отличающийся сложной неповторяющейся временной зависимостью.
Звуковой удар – это кратковременное звуковое воздействие: хлопок, взрыв.
Объективные
характеристики звука
Частота
Амплитуда колебаний
Форма колебаний
Гармонический спектр
Интенсивность звука
Звуковое давление
Субъективные
характеристики звука
Высота – определяется высотой основного тона
Тембр – определяется спектральным составом
Громкость – характеризует уровень слухового ощущения

Звук – продольная механическая волна определенной частоты
Звуковые волны с частотами от 16 до 2104 Гц воздействуют на органы слуха человека, вызывают слуховые ощущения и называются слышимыми звуками. Звуковые волны с частотами менее 16 Гц называются инфразвуками, а с частотами более 2104 Гц – ультразвуками.
Восприятие звука органами слуха зависит от того, какие частоты входят в состав звуковой волны.
Скорость звука в воздухе
приблизительно 330 м/с
Высота тона зависит от частоты: чем больше частота, тем выше тон.
Громкость звука зависит от интенсивности звука, т.е. определяется амплитудой колебаний в звуковой волне. Наибольшей чувствительностью органы слуха обладают к звукам с частотами от 700 до 6000 Гц.

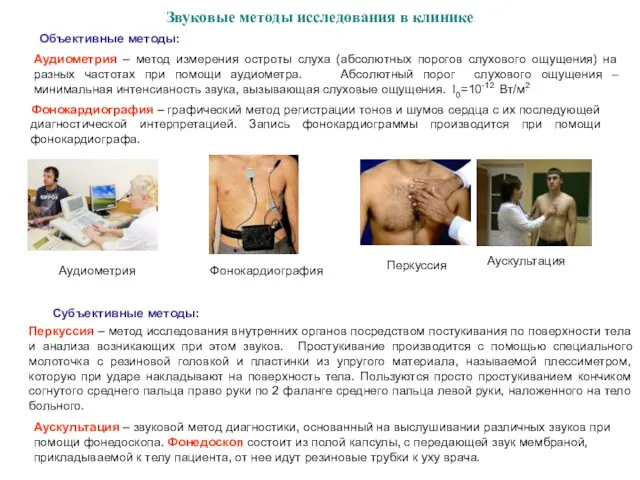
Звуковые методы исследования в клинике
Аудиометрия
Объективные методы:
Аудиометрия – метод измерения остроты слуха (абсолютных порогов слухового ощущения) на разных частотах при помощи аудиометра. Абсолютный порог слухового ощущения – минимальная интенсивность звука, вызывающая слуховые ощущения. I0=10-12 Вт/м2
Фонокардиография – графический метод регистрации тонов и шумов сердца с их последующей диагностической интерпретацией. Запись фонокардиограммы производится при помощи фонокардиографа.
Субъективные методы:
Перкуссия – метод исследования внутренних органов посредством постукивания по поверхности тела и анализа возникающих при этом звуков. Простукивание производится с помощью специального молоточка с резиновой головкой и пластинки из упругого материала, называемой плессиметром, которую при ударе накладывают на поверхность тела. Пользуются просто простукиванием кончиком согнутого среднего пальца право руки по 2 фаланге среднего пальца левой руки, наложенного на тело больного.
Аускультация – звуковой метод диагностики, основанный на выслушивании различных звуков при помощи фонедоскопа. Фонедоскоп состоит из полой капсулы, с передающей звук мембраной, прикладываемой к телу пациента, от нее идут резиновые трубки к уху врача.
Перкуссия
Аускультация
Фонокардиография

Реология (от греч. rhéos — течение, поток и... логия), наука о деформациях и текучести вещества. Р. рассматривает процессы, связанные с необратимыми остаточными деформациями и течением разнообразных вязких и пластических материалов (неньютоновских жидкостей, дисперсных систем и др.), а также явления релаксации напряжений, упругого последействия и т.д.
Биореология исследует течение разнообразных биологических жидкостей (например, крови, синовиальной, плевральной и др.), деформации различных тканей (мышц, костей, кровеносных сосудов) у человека и животных.

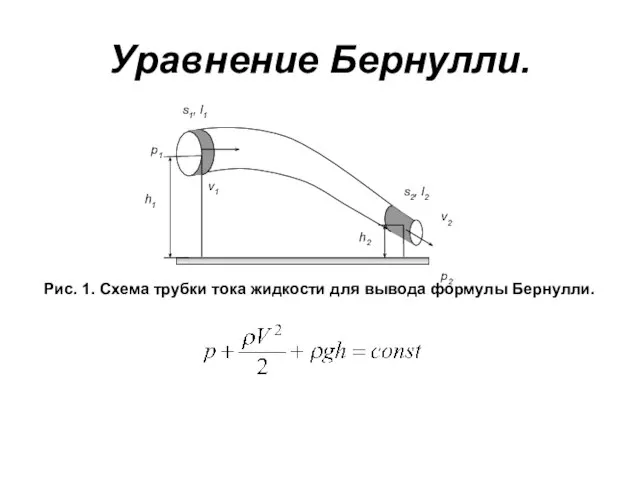
Уравнение Бернулли.
Рис. 1. Схема трубки тока жидкости для вывода формулы Бернулли.

Внутреннее трение (вязкость) жидкости.
Формула Ньютона.
Рассмотрим ламинарный поток вязкой жидкости по горизонтальному руслу.
Fтр =
.

Течение вязкой жидкости. Формула Пуазейля.

Методы определения вязкости жидкости.
Совокупность методов измерения вязкости называют вискозиметрией, и приборы, используемые для таких целей - вискозиметрами.
Капиллярные методы основаны на законе Пуазейля и заключаются в измерении времени протекания через капилляр жидкости известной массы под действием силы тяжести при определенном перепаде давлений.
Рис. 7. Вискозиметр Оствальда.
1 – измерительный резервуар,
2 – кольцевые метки,
3 – резервуар,
4 – капилляр,
5 – груша.
Вискозиметр Оствальда.
Вискозиметр Оствальда представлен на рисунке 7.

Метод падающего шарика (метод Стокса)