Слайд 2Напряженность результирующего поля равна
геометрической (векторной) сумме напряженностей полей, создаваемых каждым зарядом

в отдельности:
Слайд 3Потенциал результирующего поля равен
алгебраической сумме потенциалов этих полей:

Слайд 4Найти потенциал намного проще, поскольку это скалярная величина.

Слайд 5Расчет полей по методу суперпозиции
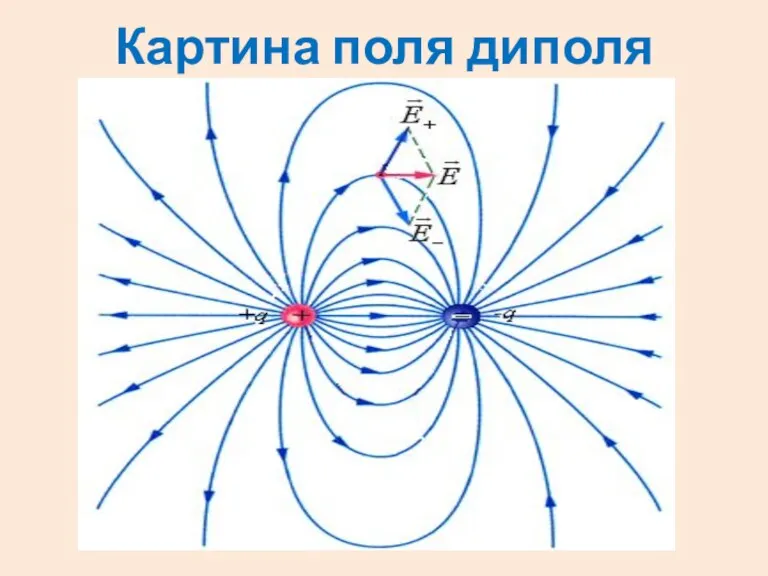
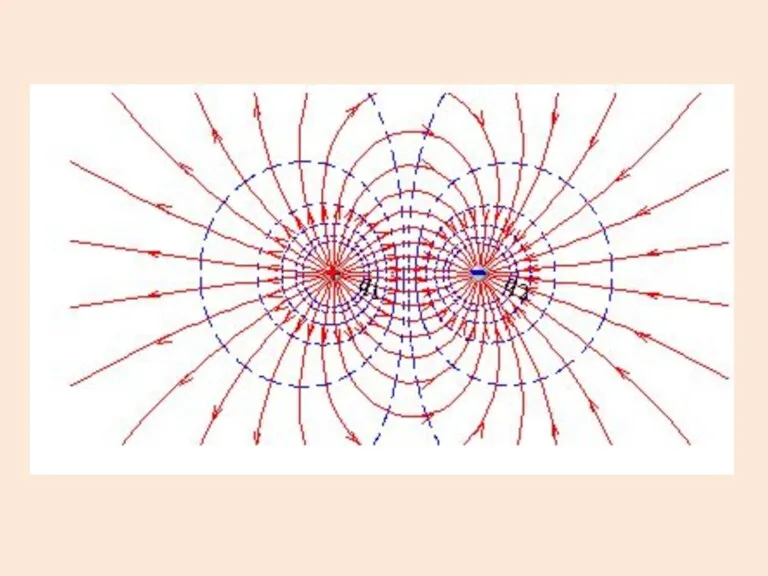
1. Поле диполя.
Электрический диполь – система двух зарядов

равных по величине и противоположных по знаку.
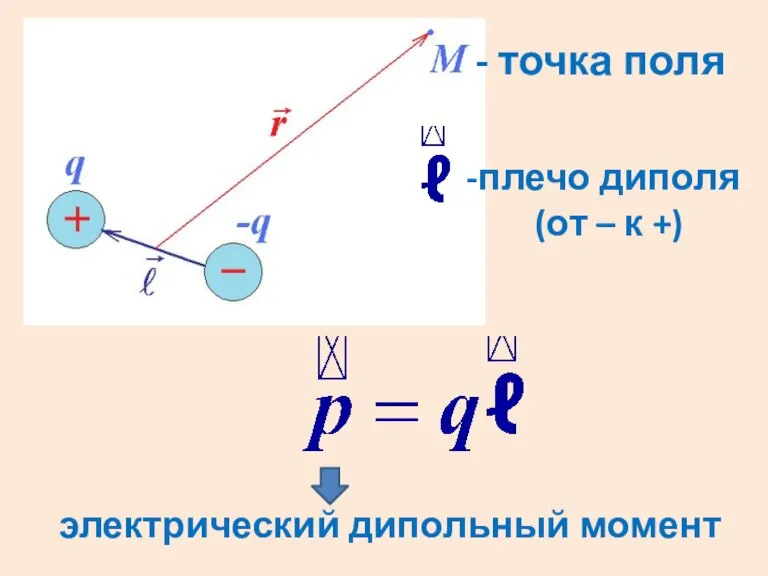
Слайд 6- точка поля
плечо диполя (от – к +)
электрический дипольный момент
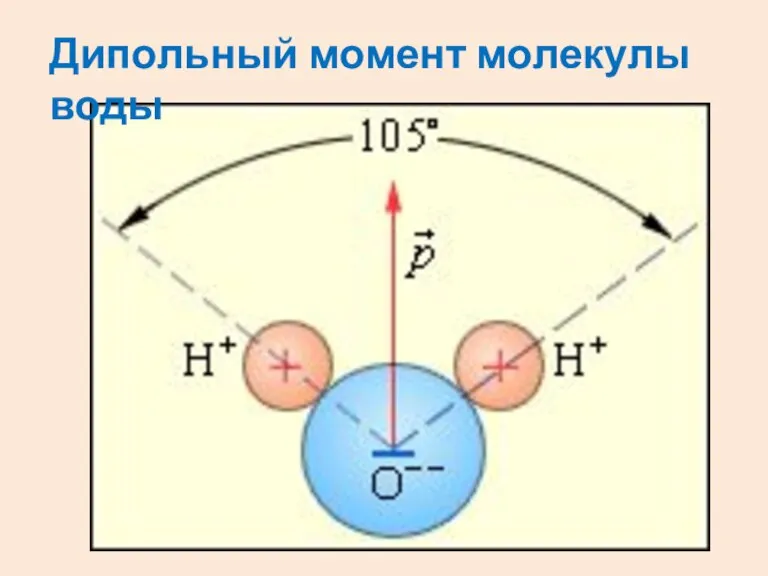
Слайд 7Дипольный момент молекулы воды
Слайд 8Дипольный момент измеряется в

Слайд 9Диполь можно изобразить так:
Если , диполь называют точечным.

Слайд 10Будем искать поле на оси диполя (обозначим ) и на перпендикуляре к
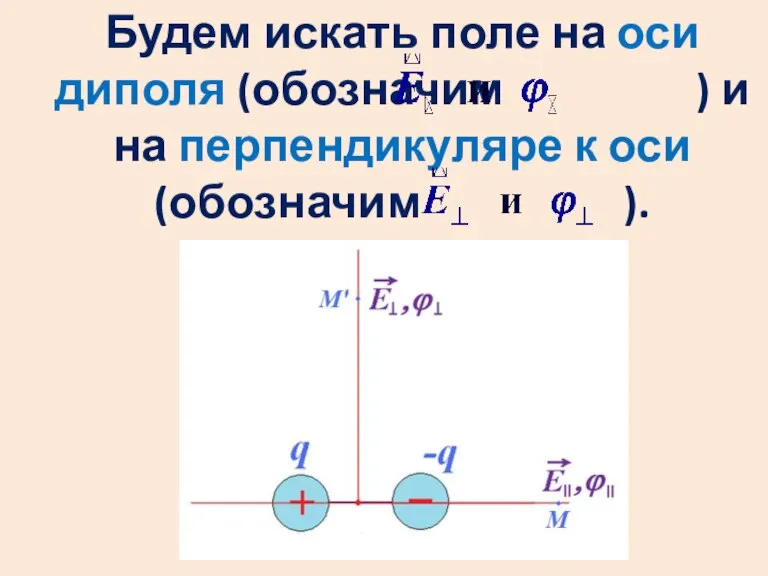
оси
(обозначим ).
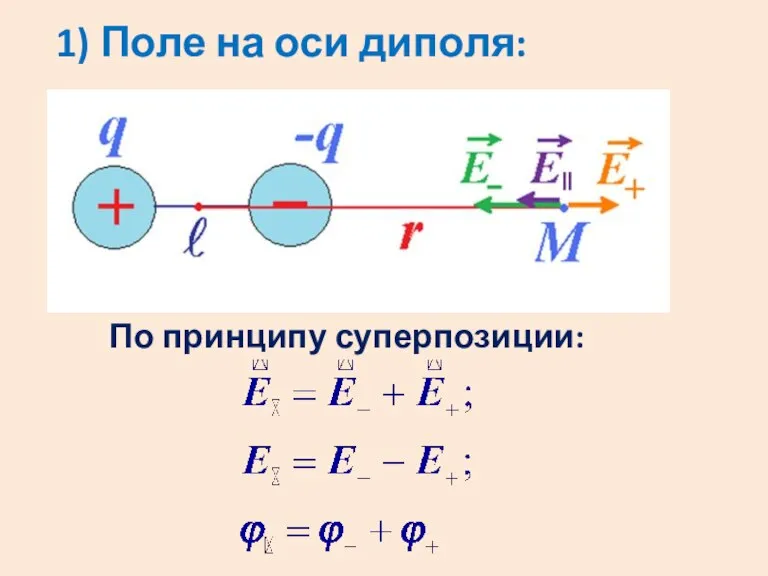
Слайд 111) Поле на оси диполя:
По принципу суперпозиции:
Слайд 12Пусть расстояние от +q до М,
расстояние от –q до М.
Для точечного

диполя
Слайд 14Заметим, что . Тогда
А со стороны положительного заряда

Слайд 15Потенциал поля диполя убывает как квадрат расстояния – быстрее, чем для точечного

заряда.
Слайд 17Напряженность поля диполя убывает как куб расстояния – тоже быстрее, чем у

точечного заряда.
Слайд 182) Поле на перпендикуляре к оси диполя
Потенциал искать не надо. Ясно, что
Ищем
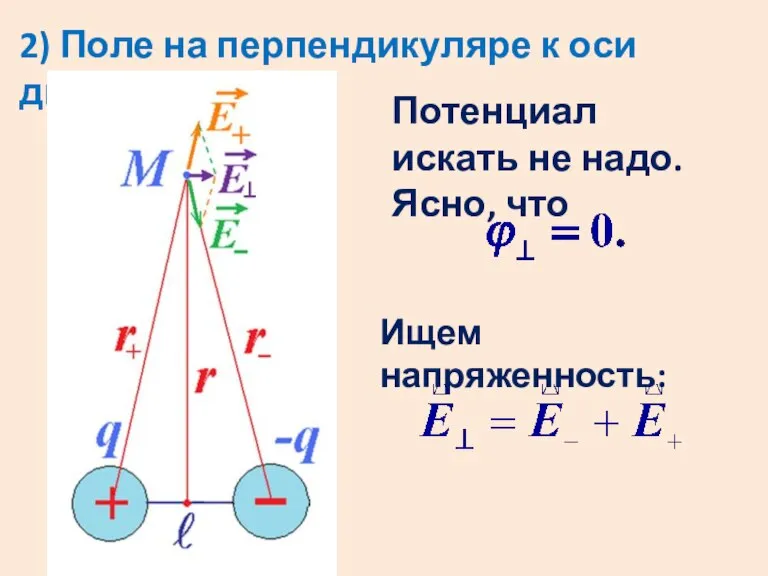
напряженность:
Слайд 19Большие и маленькие треугольники на рисунке подобны. Тогда

Слайд 20Тоже убывает как куб расстояния.

Слайд 23Непрерывно распределенный заряд
Пусть заряд – не точечный, а непрерывно распределен по протяженному

телу.
Слайд 24Линейная плотность заряда – заряд, приходящийся на единицу длины.
1 м
λ

Слайд 25Поверхностная плотность заряда – заряд единицы площади.
σ
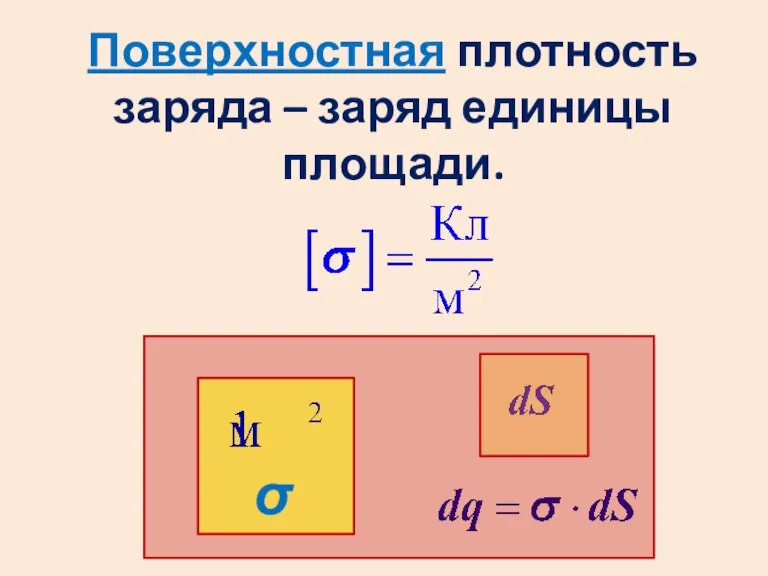
Слайд 26Объемная плотность заряда – заряд единицы объема.
Заряд объема :

Слайд 272. Поле бесконечной однородно заряженной нити
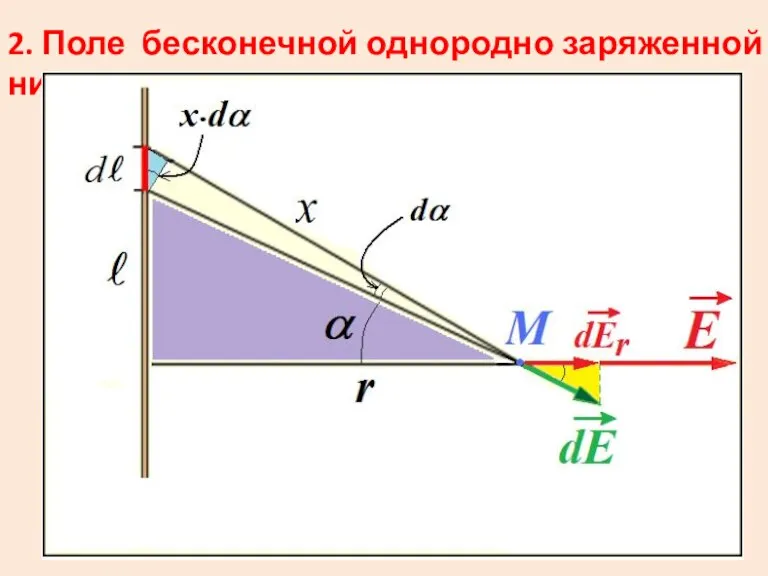
Слайд 28Каждый элемент длины создает напряженность . Эти векторы образуют “веер”.
Этот вектор

направлен горизонтально, т. к. в вертикальном направлении в сумме имеем нуль.
Слайд 29Горизонтальная компонента каждого вектора равна .
На рисунке три цветных треугольника подобны. Острый

уголок при вершине равен α .
Слайд 31Интегрировать будем по углу. Верхняя и нижняя части нити дают равный вклад.

Угол меняем в пределах от нуля до π/2, а интеграл умножим на 2. Остается выразить dl и x.
Слайд 32В верхнем маленьком треугольнике
В большом треугольнике

Слайд 34 Для вакуума
Напряженность поля нити:



























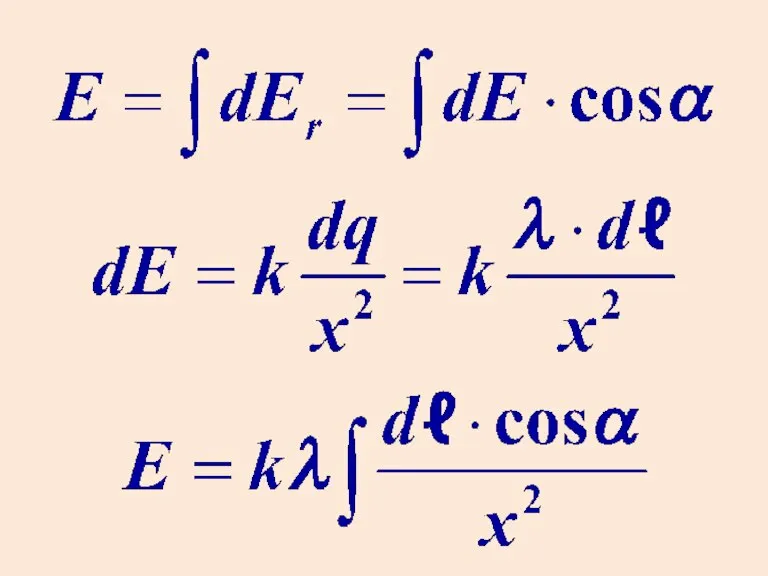




 Релаксация спинового ансамбля
Релаксация спинового ансамбля Основы электротехники. Основные понятия и законы
Основы электротехники. Основные понятия и законы Корпускулярно-волновой дуализм
Корпускулярно-волновой дуализм Вакуумная, компрессорная техника и пневмосистемы
Вакуумная, компрессорная техника и пневмосистемы Как сберечь тепло в доме
Как сберечь тепло в доме Производство и передача электроэнергии в РФ
Производство и передача электроэнергии в РФ Движение в физике. Звук
Движение в физике. Звук Основные законы социальной динамики. Лекция 3
Основные законы социальной динамики. Лекция 3 Летняя практика
Летняя практика Электролиз. Удивительный мир гальваники
Электролиз. Удивительный мир гальваники Четырехмерный мир (пространство Минковского)
Четырехмерный мир (пространство Минковского) Расчет шатуна. Лекция №11а
Расчет шатуна. Лекция №11а Газовые законы
Газовые законы Деятельность и достижения Галилео Галилея в механике
Деятельность и достижения Галилео Галилея в механике Самолётные ответчики. Основы радиолокации
Самолётные ответчики. Основы радиолокации Интерференция волн
Интерференция волн Эстелайт. Светоотверждаемые, нанокомпозитные материалы
Эстелайт. Светоотверждаемые, нанокомпозитные материалы ИК-спектроскопия
ИК-спектроскопия Отрасль, которая производит электроэнергию и передает её на расстояние по линиям электропередач.
Отрасль, которая производит электроэнергию и передает её на расстояние по линиям электропередач. Эксимерные лазеры
Эксимерные лазеры Дисперсия света. Опыт И. Ньютона
Дисперсия света. Опыт И. Ньютона Презентация на тему Равнодействующие силы. Сила трения
Презентация на тему Равнодействующие силы. Сила трения  Физика и техника
Физика и техника Физика и техника
Физика и техника Ядерный реактор. АЭС
Ядерный реактор. АЭС Постоянные магниты. Магнитное поле Земли
Постоянные магниты. Магнитное поле Земли Оптика. Законы отражения
Оптика. Законы отражения Закон сохранения энергии
Закон сохранения энергии