Плоская система сходящихся сил. Определение равнодействующей аналитическим способом

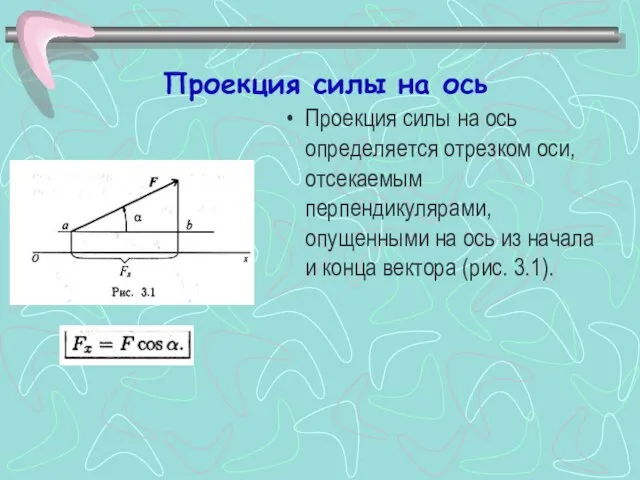
Проекция силы на ось
Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 3.1).

Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).

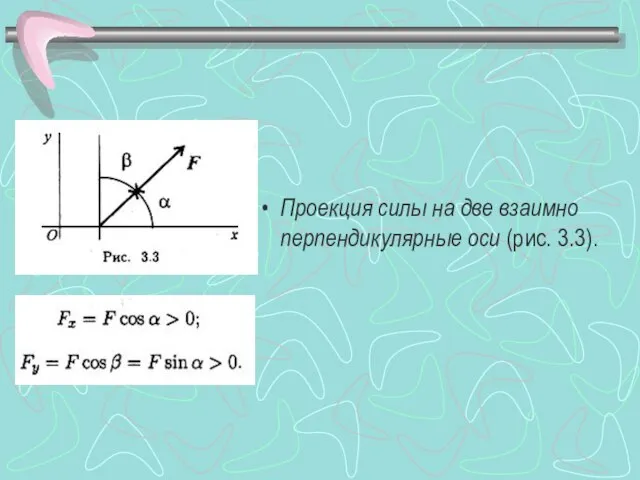
Проекция силы на две взаимно перпендикулярные оси (рис. 3.3).

Определение равнодействующей системы сил аналитическим способом
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геометрическим способом.
Выберем систему координат, определим пропорции всех заданных векторов на эти оси (рис. 3.4, а).
Складываем проекции всех векторов на оси х и у (рис. 3.4, б).

Модуль (величину) равнодействующей можно найти по известным проекциям:
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5).

Условия равновесия плоской системы сходящихся сил в аналитической форме
Исходя из того, что равнодействующая равна нулю, получим:

Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.
Система уравнений равновесия плоской сходящейся системы сил:
В задачах координатные оси выбирают так, чтобы решение было наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.

Пример 1. Определить величины и знаки проекций представленных на рис. 3.6 сил.

Пример 2. Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом.
1. Определяем проекции всех сил системы на Ох (рис. 3.7, а):

F∑x = 8,66 – 20 + 10,6 = - 0,735 кН
Сложив алгебраически проекции, получим проекцию равнодействующей на ось Ох.
Знак говорит о том, что равнодействующая направлен влево.

2. Определяем проекции всех сил на ось Оу значения проекций, получим величину проекции Оу.
Сложив алгебраически значения проекций, получим величину проекции равнодействующей на ось Оу.
Знак проекции соответствует направлению вниз. Следовательно, равнодействующая направлена влево и вниз (рис. 3.7б).

Пример 3. Система трех сил находится в равновесии. Известны проекции двух сил системы на взаимно перпендикулярные оси Ох и Оу:
Flx = 10 кН; F2x = 5 кН;
F1y = - 2 кН; F2y = 6 кН.
Определить, чему равна и как направлена третья сила системы.
Решение
1. Из уравнений равновесия системы определяем: