Содержание
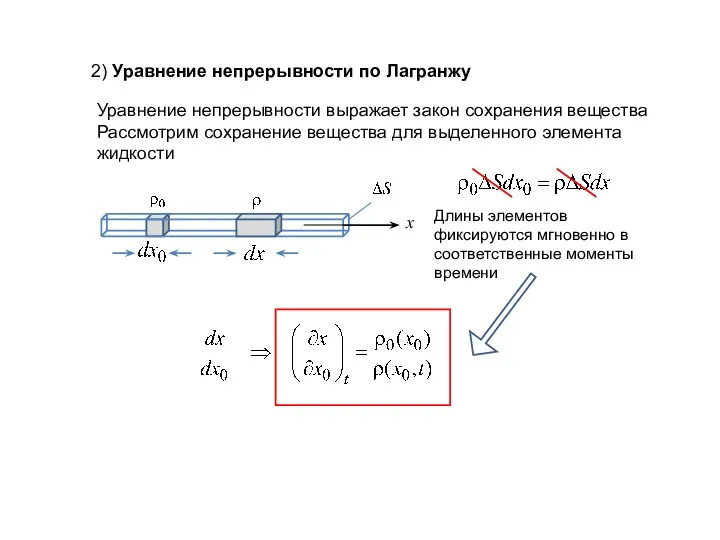
- 2. 2) Уравнение непрерывности по Лагранжу Уравнение непрерывности выражает закон сохранения вещества Рассмотрим сохранение вещества для выделенного
- 3. 3) Уравнение движения по Лагранжу Выделенный элемент dx испытывает ускорение Находится под действием разности сил давления
- 4. Из закона сохранения вещества Поэтому 4) Решение задачи По условиям задачи Уравнение движения дает Величину начального
- 5. Отсюда имеем связь лагранжевой координаты x c ее начальным значением Цель решения – нахождение распределения плотности
- 6. Обозначая исходное распределение плотности имеем окончательно 5) Обсуждение и выводы Вместо можно рассмотреть используя (1) Однако
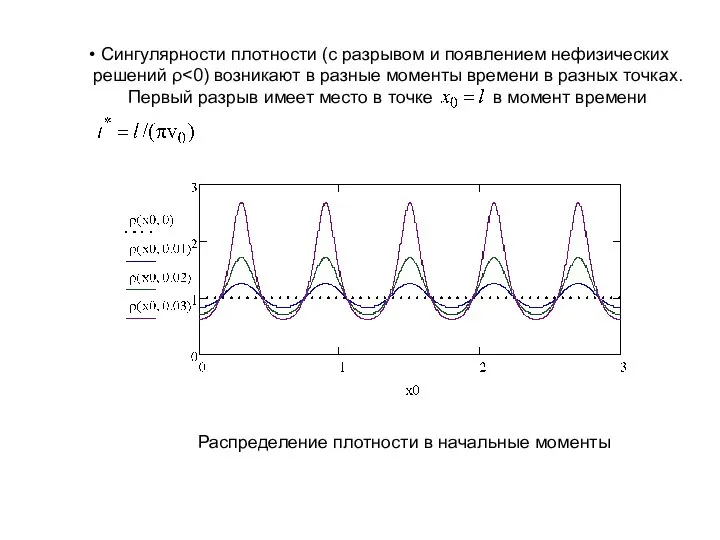
- 7. Сингулярности плотности (с разрывом и появлением нефизических решений ρ Первый разрыв имеет место в точке в
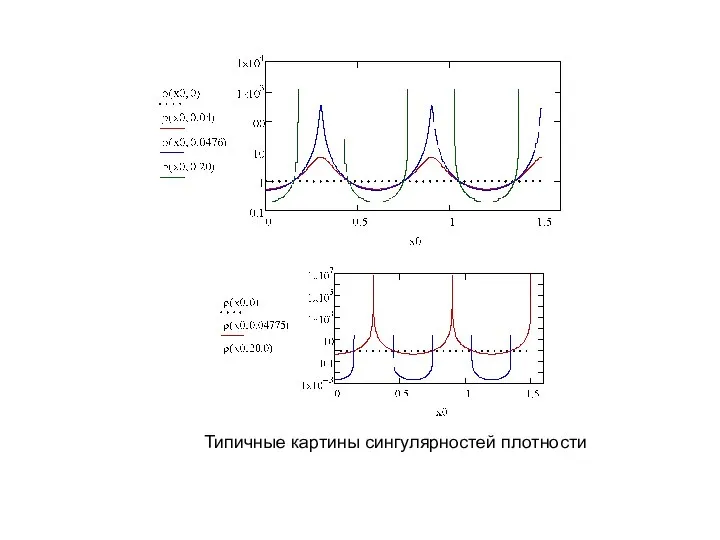
- 8. Типичные картины сингулярностей плотности
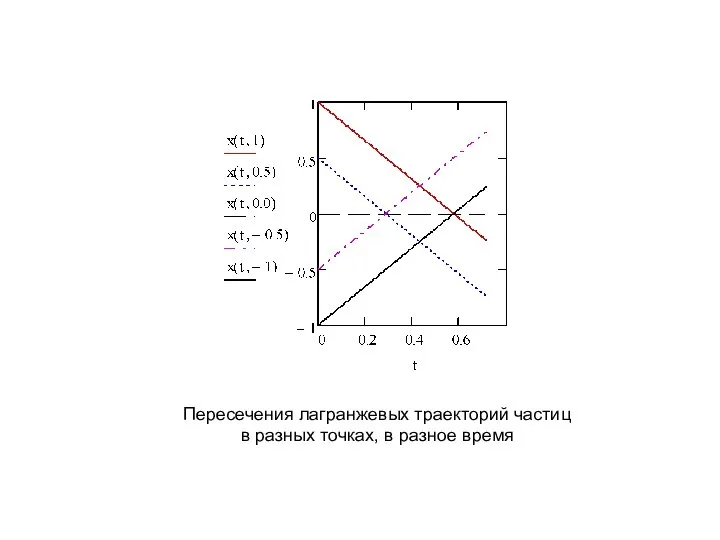
- 9. Пересечения лагранжевых траекторий частиц в разных точках, в разное время
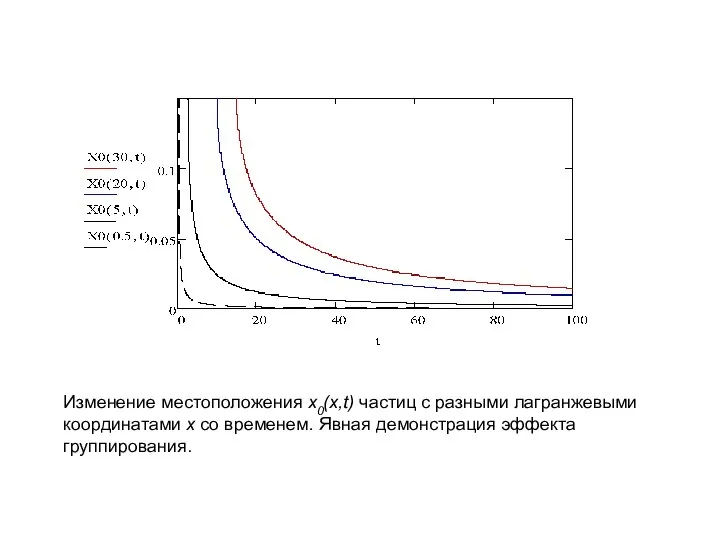
- 10. Изменение местоположения x0(x,t) частиц с разными лагранжевыми координатами x со временем. Явная демонстрация эффекта группирования.
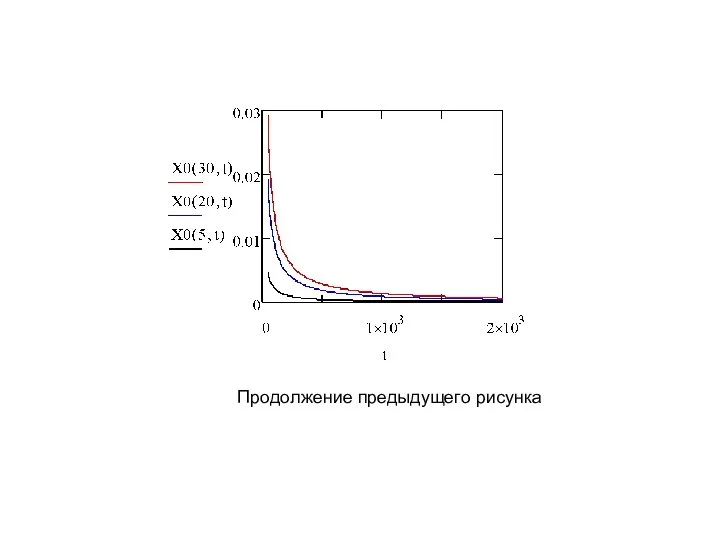
- 11. Продолжение предыдущего рисунка
- 13. Скачать презентацию




 Многофакторное прогнозирование экологических характеристик дизеля на основе вычислительных методов
Многофакторное прогнозирование экологических характеристик дизеля на основе вычислительных методов Формула бинома Ньютона
Формула бинома Ньютона Изображения, даваемые линзой
Изображения, даваемые линзой Спектры. Устройство спектроскопа
Спектры. Устройство спектроскопа Механические колебания и волны
Механические колебания и волны Простейшие оптические приборы
Простейшие оптические приборы Квантовые постулаты Бора
Квантовые постулаты Бора О, сколько нам открытий чудных…
О, сколько нам открытий чудных… 3-й закон Ньютона
3-й закон Ньютона Презентация на тему Рентгеновское излучение. История открытия
Презентация на тему Рентгеновское излучение. История открытия  Урок открытия нового знания (ОНЗ)
Урок открытия нового знания (ОНЗ) Презентация на тему Взаимодействие тел. Масса тела
Презентация на тему Взаимодействие тел. Масса тела  Классическое определение вероятности Решение задач.
Классическое определение вероятности Решение задач. Гидростатическое давление в точке. Тема 1
Гидростатическое давление в точке. Тема 1 Электромагнитная индукция
Электромагнитная индукция Перспективный бортовой водородный стандарт частоты космического применения
Перспективный бортовой водородный стандарт частоты космического применения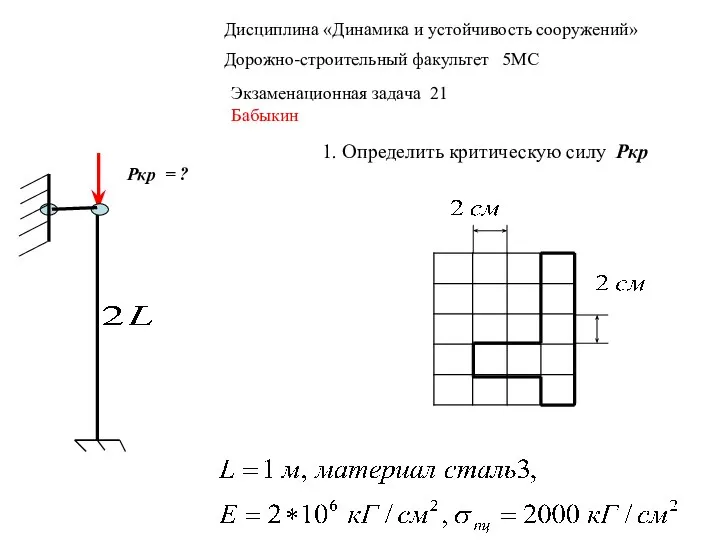 Динамика. Экзаменационные задачи 21-43
Динамика. Экзаменационные задачи 21-43 2Методы расчетов электрических нагрузок и выбор сечения проводников
2Методы расчетов электрических нагрузок и выбор сечения проводников Дифракция в сходящихся лучах (дифракция Френеля)
Дифракция в сходящихся лучах (дифракция Френеля) Получение переменного электрического тока. (Физика 11 класс). Разработала учитель физики МОУ СОШ № 8 г. Тюмени Жижимонтова Т.Г.
Получение переменного электрического тока. (Физика 11 класс). Разработала учитель физики МОУ СОШ № 8 г. Тюмени Жижимонтова Т.Г. Модельный ряд двигателей ЗМЗ
Модельный ряд двигателей ЗМЗ Тепловая генерация энергии на основе холодного ядерного синтеза
Тепловая генерация энергии на основе холодного ядерного синтеза Электрическое сопротивление
Электрическое сопротивление Устойчивость режима работы реактора. Лекция № 5
Устойчивость режима работы реактора. Лекция № 5 Соединение конденсаторов
Соединение конденсаторов Презентация на тему Электрическая цепь
Презентация на тему Электрическая цепь  Линзы. Построения в линзах. 11 класс
Линзы. Построения в линзах. 11 класс ТMM структура. Лекция 1
ТMM структура. Лекция 1