Молекулярно-кинетический подход применительно к расчету тепловой нагрузки при пленочном кипении

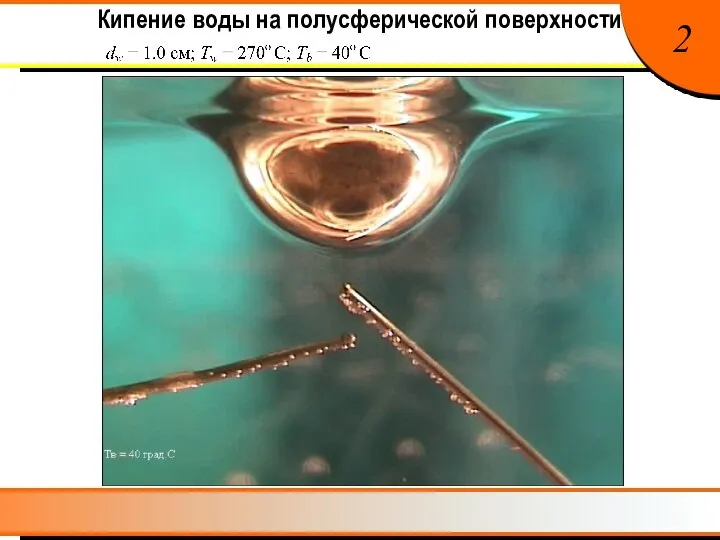
Кипение воды на полусферической поверхности
2

Юрий Петрович Ивочкин Константин Кубриков

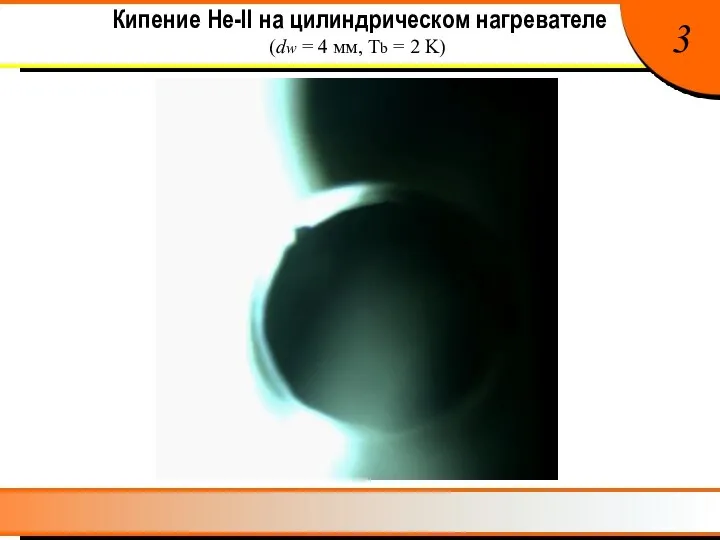
Кипение He-II на цилиндрическом нагревателе
(dw = 4 мм, Tb = 2 K)
3

Пленочное кипение Не-II на цилиндре
4

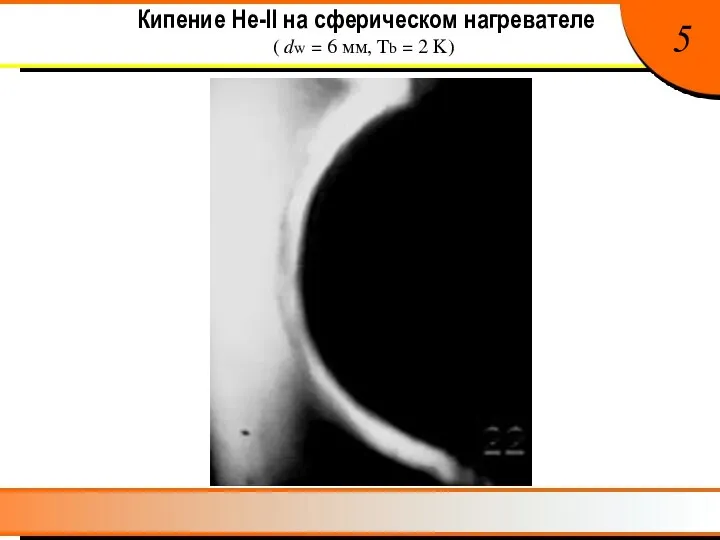
Кипение He-II на сферическом нагревателе
(dw = 6 мм, Tb = 2 K )
5

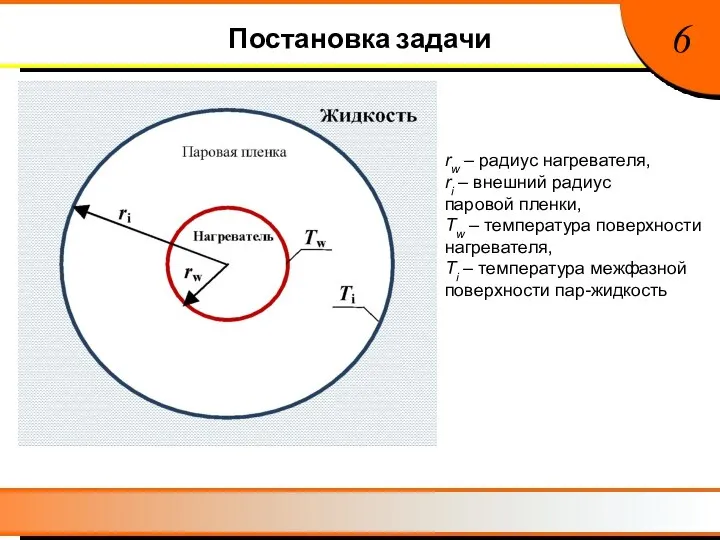
Постановка задачи
6
rw – радиус нагревателя,
ri – внешний радиус
паровой пленки,
Tw – температура поверхности
нагревателя,
Ti – температура межфазной
поверхности пар-жидкость

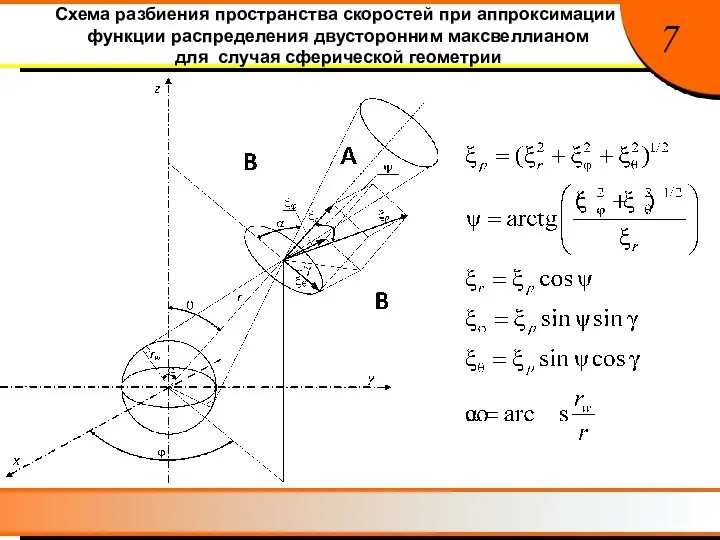
Схема разбиения пространства скоростей при аппроксимации
функции распределения двусторонним максвеллианом
для случая сферической геометрии
7

Аппроксимация функции распределения
8

Уравнение Больцмана для
сферически симметричной задачи
9 a
где - компоненты вектора скорости в сферической системе координат.

Интегральное уравнение для сферической геометрии
задачи, полученное из кинетического уравнения Больцмана 9 b

Результаты интегрирования уравнения
10

Формула для плотности теплового потока
11

12
При решении уравнения Больцмана граничное условие при фиксировано:
При тонких пленках задачу для кинетического уравнения Больцмана можно считать плоской и одномерной:
С учетом этого аналитическая формула для теплового потока приобретает вид:
В результате решения кинетического уравнения Больцмана получено давление в пленке и плотность теплового потока на нагревателе .
Сравнение с численным решением
кинетического уравнения Больцмана для тонких пленок
(тестовая задача)

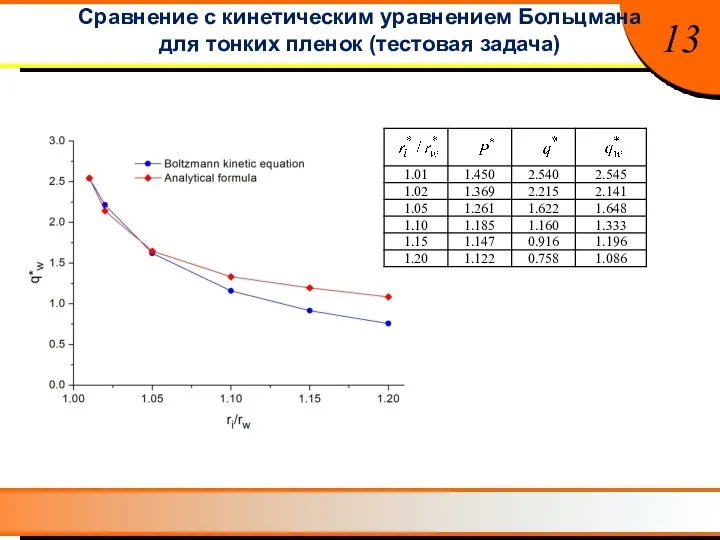
13
Сравнение с кинетическим уравнением Больцмана
для тонких пленок (тестовая задача)

14
Численное решение уравнения Больцмана
в сферической постановке
Уравнение Больцмана для сферически симметричной задачи имеет вид:
где - компоненты вектора скорости в сферической системе координат.
Однако описывать движение молекул в декартовой системе координат является более естественным. Перевод компонентов скорости в сферическую систему
существенно осложняет вычисление интеграла столкновений;
требует использования более сложных разностных схем для левой части уравнения.

15
Численное решение уравнения Больцмана
в сферической постановке
Построение конечноразностных схем для сферического уравнения при сохранении декартовых координат в скоростном пространстве.
Рассмотрим, как частицы, имеющие скорость , пронизывают тонкие сферические слои.
Баланс массы для i-го слоя:
где - функция распределения, - номер сферического слоя, - внешний и внутренний радиус -го сферического слоя, соответственно.

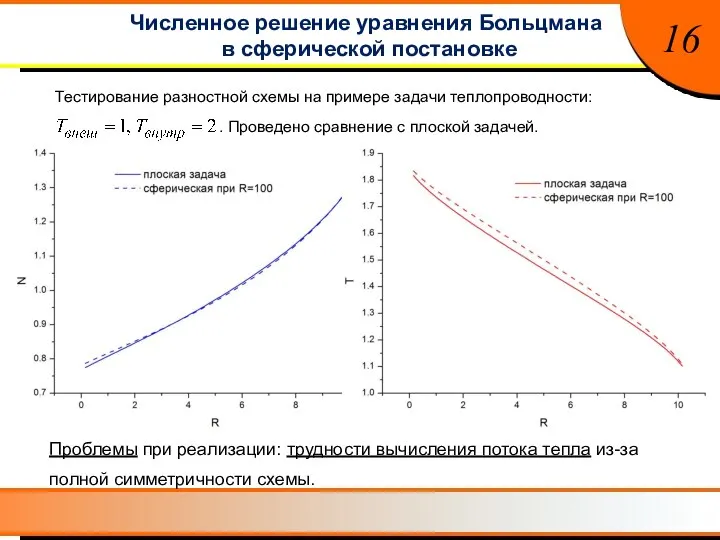
Численное решение уравнения Больцмана
в сферической постановке
16
Тестирование разностной схемы на примере задачи теплопроводности:
. Проведено сравнение с плоской задачей.
Проблемы при реализации: трудности вычисления потока тепла из-за полной симметричности схемы.

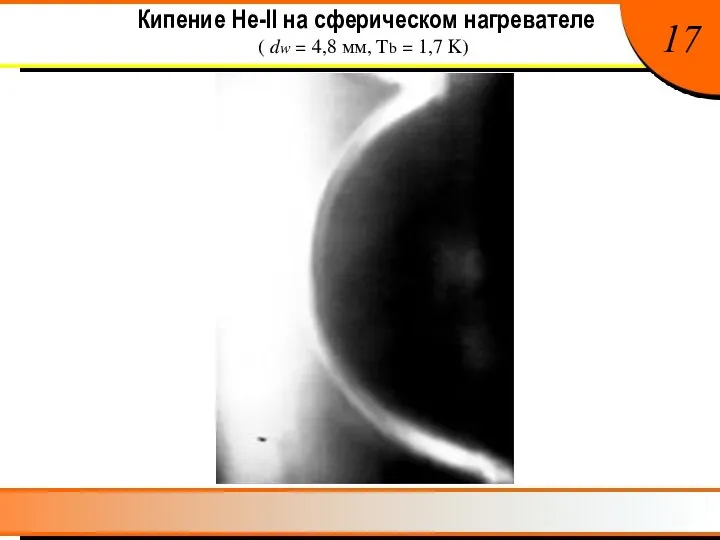
Кипение He-II на сферическом нагревателе
(dw = 4,8 мм, Tb = 1,7 K )
17

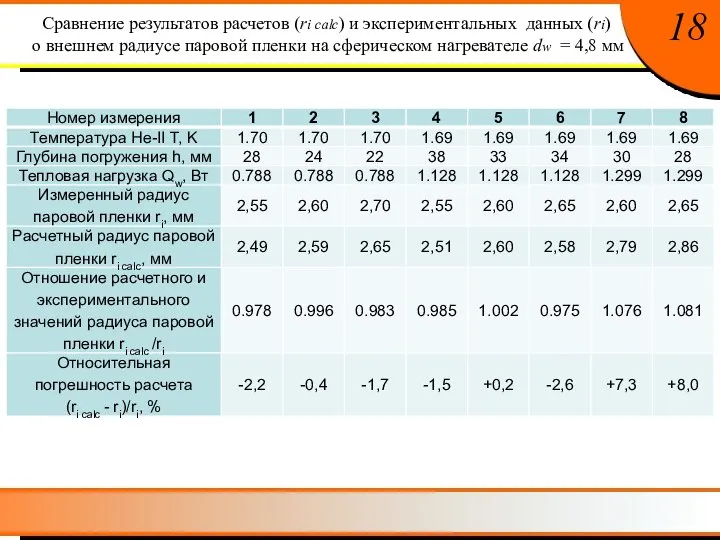
18
Сравнение результатов расчетов (ri calc) и экспериментальных данных (ri)
о внешнем радиусе паровой пленки на сферическом нагревателе dw = 4,8 мм

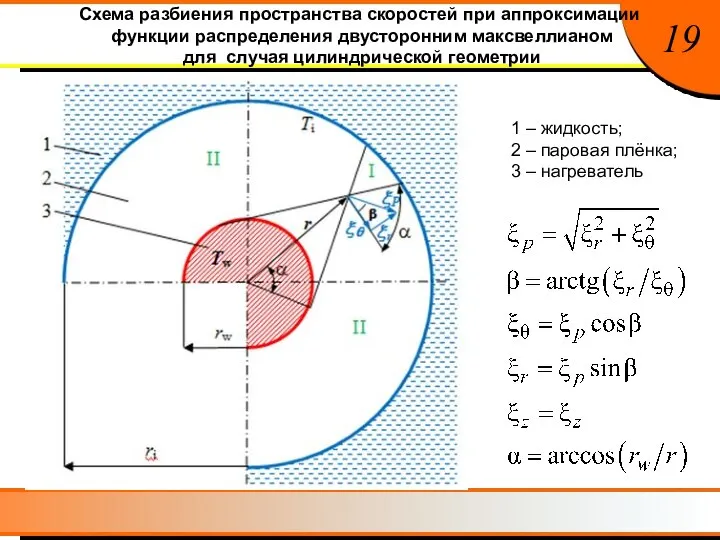
Схема разбиения пространства скоростей при аппроксимации
функции распределения двусторонним максвеллианом
для случая цилиндрической геометрии
19
1 – жидкость;
2 – паровая плёнка;
3 – нагреватель

Интегральное уравнение для цилиндрической
геометрии задачи, полученное из кинетического уравнения
Больцмана
20

Аппроксимация функции распределения
21

Результаты интегрирования уравнения
22

Формула для плотности теплового потока
23

24
Пленочное кипение Не-II на цилиндре

Примеры пленочного кипения на цилиндре
25