Слайд 2Некоторые основные понятия ПМ
Прикладная механика представляет собой комплексную дисциплину, в которой излагаются

основные положения о прочности и жесткости материалов и методах расчета конструктивных элементов, а также изучает сами механизмы и машины.
Элемент конструкции – некоторая часть конструкции (сооружения, механизма), предназначенная для расчета.
Прочность – способность тела (детали, элемента конструкции) сопротивляться внешним воздействиям (силовым, температурным и т.д.) без разрушения, или без появления в нем пластических деформаций.
Жесткость – способность тела незначительно изменять свой объем и форму под действием внешних сил.
Деформации, исчезающие после снятия нагрузок, называются упругими.
Деформации, остающиеся в теле после снятия нагрузок, называются остаточными или пластическими.
Устойчивость – способность конструкции сохранять первоначальную форму или находиться в состоянии устойчивого равновесия.
Долговечность – способность конструкции сохранять необходимые для эксплуатации служебные свойства в течение заранее предусмотренного срока времени.
Механические свойства – характеристики материала, описывающие его поведение при внешних силовых воздействиях.
Слайд 3Некоторые основные понятия ПМ
Реальный объект – исследуемый элемент конструкции, взятый с учетом

всех своих особенностей: геометрических, физических, механических и других.
Расчетная схема – это реальный объект, у которого отброшены все детали (особенности), не связанные с расчетом, а их влияние заменено силовыми воздействиями.
Для перехода от реального объекта к расчетной схеме (с целью упрощения расчетов) необходимо вводить схематизацию понятий.
Можно выделить следующие типы схематизации:
- геометрическая схематизация;
- физическая схематизация;
- силовая схематизация.
Слайд 4Геометрическая схематизация
(модель формы)
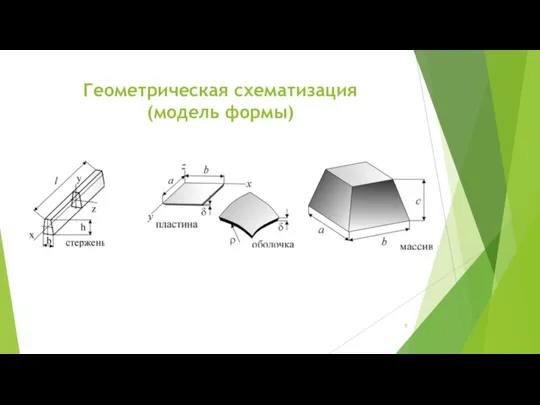
Для схематизации формы реальных объектов в сопротивлении материалов используются

следующие основные типы элементов: стержень (брус, балка, вал), пластина (плита, оболочка) и массивное тело.
Стержень – элемент конструкции, у которого два измерения малы по сравнению с третьим.
Пластина – элемент конструкции, у которого одно измерение (толщина) мало по сравнению с двумя другими.
Массивное тело – элемент конструкции, у которого все размеры имеют один порядок.
Слайд 5Геометрическая схематизация
(модель формы)
Слайд 6Физическая схематизация
(модель материала)
Материал элементов конструкций будем в дальнейшем считать сплошным, однородным,

изотропным и линейно-упругим.
Сплошной материал – материал, не имеющий разрывов, пустот, трещин, пор, включений и т. д.
Однородный материал – материал, в каждой точке которого механические свойства одинаковы и не зависят от величины выделенного объема.
Изотропный материал – материал, свойства которого одинаковы по всем направлениям.
Упругий материал – материал, обладающий способностью восстанавливать первоначальные форму и размеры тела после снятия внешней нагрузки.
Линейно-упругий материал – материал, подчиняющийся закону Гука. Закон Гука: «Перемещения точек упругого тела (в известных пределах нагружения) прямо пропорциональны силам, вызывающим эти перемещения».
Слайд 7Силовая схематизация
(модель нагружения)
Внешние силы – силы взаимодействия между рассматриваемым элементом

конструкции и другими телами, связанными с ним.
Классификация внешних сил по способу приложения:
Сосредоточенные нагрузки – силы и моменты, площадь действия которых мала по сравнению с размерами объекта (приложены в точке). Обозначения: F (Р), М (T). Единицы измерения: [F]=H; [M]=Н·м в СИ или [F]=кг; [M]=кг·м в технической системе.
Распределенные нагрузки – силы, действующие а) на некоторой длине, б) по некоторой площадке, в) по объему. Обозначение q. Единицы измерения: а) [q]=H/м, кг/см, кг/мм; б) [q]=H/м2, кг/см2, кг/мм2; в) [q]=H/м3, кг/см3, кг/мм3 и т. д.
Слайд 8Силовая схематизация
(модель нагружения)
Классификация внешних сил по характеру изменения во времени:

Статические нагрузки медленно и плавно возрастают от нуля до своего конечного значения, а затем остаются неизменными.
Динамические нагрузки сопровождаются ускорениями как деформированного тела, так и взаимодействующих с ним тел.
К динамическим нагрузкам относятся, например, силы действующие на ускорено движущиеся тела, ударные нагрузки и т. д.
Повторно-переменные нагрузки – силы непрерывно и периодически изменяющиеся во времени.
Слайд 9Несвободное твердое тело. Связи. Реакции связей.
Твердое тело называется свободным, если оно может

перемещаться в пространстве в любом направлении.
Тело, ограничивающее свободу движения данного твердого тела, является по отношению к нему связью.
Твердое тело, свобода движения которого ограничена связями, называется несвободным.
Все силы, действующие на несвободное твердое тело, наряду с делением на внешние и внутренние силы, можно разделить на задаваемые силы и реакции связей.
Задаваемые силы (активные) выражают действие на твердое тело других тел, вызывающих или способных вызвать изменение его кинематического состояния.
Реакцией связи называется сила или система сил, выражающая механическое действие связи на тело.
Одним из основных положений механики является принцип освобождаемости твердых тел от связей, согласно которому несвободное твердое тело можно рассматривать как свободное, на которое, кроме задаваемых сил, действуют реакции связей.
Полученное в результате освобождения от связей свободное тело находится под действием задаваемых сил и реакций связей.
Слайд 10Основные типы связей и их реакции

Слайд 11Основные типы связей и их реакции

Слайд 12Основные типы связей и их реакции

Слайд 13Системы сил
Система сил может быть:
плоской, если все силы лежат в одной

плоскости;
пространственной, если силы не лежат в одной плоскости.
Силы могут пересекаться в одной точке, то тогда эта система называется
системой сходящихся сил:
это может быть как на плоскости (плоская система сходящихся сил);
так и в пространстве (пространственная система сходящихся сил).
Силы могут быть параллельны друг другу, то тогда эта система называется
системой параллельных сил:
это может быть как на плоскости (плоская система параллельных сил);
так и в пространстве (пространственная система параллельных сил).
Силы могут произвольно располагаться:
на плоскости (произвольная плоская система сил);
и в пространстве (произвольная пространственная система сил).
Слайд 14Понятие о статически неопределенных задачах
Если число неизвестных реакций больше, чем уравнений равновесия,

то задача статически неопределима, т.е. методами статики не решается.
Очевидно, что для пространственной системы сходящихся сил число неизвестных реакций не должно превышать трех, а для плоской - двух.
Слайд 15Определение внутренних усилий.
Метод сечений
Внутренние усилия – силы взаимодействия (сцепления) между частицами

тела, возникающие внутри элемента конструкции, как противодействие внешнему нагружению.
Внутренние усилия во всех случаях стремятся сохранить тело как единое целое, противодействуя всякой попытке изменить взаимное расположение частиц, т. е. деформировать и разрушить тело. Поэтому именно величиной внутренних усилий определяется возможность разрушения в том или ином опасном сечении элемента конструкции.
При их нахождении используется метод сечений.
Разрезая тело какой-либо плоскостью, мы мысленно разрушаем эти связи, но для равновесия системы заменяем нарушенные связи силами, которые называются внутренними. Для их определения следует рассмотреть равновесие любой части тела по одну сторону от плоскости сечения.
Слайд 16Определение внутренних усилий.
Метод сечений
Из уравнений равновесия для оставленной части тела определяется

главный вектор с проекциями N, Qy, Qz и главный момент с проекциями Mx, My, Mz. В прикладной механике (сопротивлении материалов) эти проекции часто называют внутренними усилиями.
Метод сечений позволяет отбросить ненужный для расчета элемент конструкции (или часть этого элемента), заменить его силой, действие которой будет эквивалентно действию отброшенного элемента (его части). Если задача статически определима, то для определения этой силы достаточно использовать уравнения равновесия (уравнения статики).
Рассмотрим какой-либо элемент (например, брус), находящийся в равновесии под действием внешних сил. Пусть требуется определить внутренние усилия в произвольном сечении бруса.
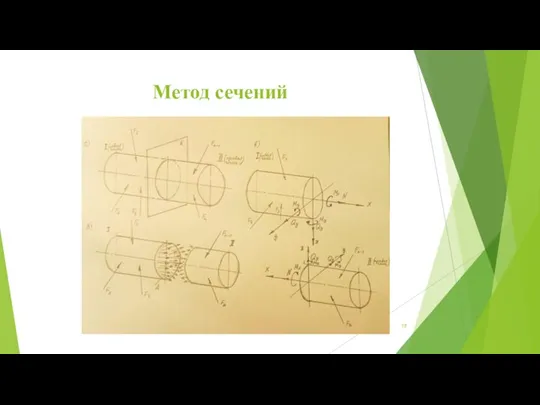
Слайд 17Определение внутренних усилий.
Метод сечений
Применим метод сечений:
а) мысленно рассечем элемент плоскостью

А–А;
б) отбросим ненужную (наиболее сложно нагруженную) часть элемента, действие отброшенной части заменим внутренними усилиями;
в) внутренние усилия приведем к главному вектору R и главному моменту M, главный вектор и главный момент разложим по трем взаимно перпендикулярным осям x, y и z (ось x – нормальна к сечению элемента);
г) внутренние усилия (N, Qy, Qz, Mx, My, Mz) определим
из уравнений равновесия оставшейся части элемента.
Слайд 19Определение внутренних усилий.
Метод сечений

Слайд 20Определение внутренних усилий.
Метод сечений

Слайд 21Определение внутренних усилий.
Метод сечений

Слайд 22Определение внутренних усилий.
Метод сечений





















 Масса, плотность, объём. (Решение задач с использованием эксперимента)
Масса, плотность, объём. (Решение задач с использованием эксперимента) Метрология. Лекция №5
Метрология. Лекция №5 Инвариантность АСР
Инвариантность АСР Тест по теме Электрический ток
Тест по теме Электрический ток Что такое электричество
Что такое электричество Задания
Задания Prezentatsia_6
Prezentatsia_6 Постоянный ток
Постоянный ток Атмосфера. Стратосфера
Атмосфера. Стратосфера Машина Голдберга
Машина Голдберга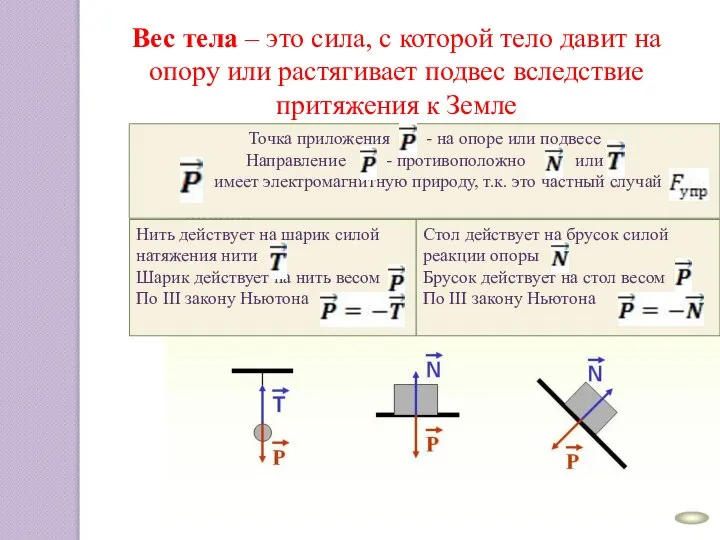 Вес тела
Вес тела Магнитное поле и его графическое изображение. Однородное и неоднородное поле. 9 класс
Магнитное поле и его графическое изображение. Однородное и неоднородное поле. 9 класс Радио- и СВЧ-волны в средствах связи
Радио- и СВЧ-волны в средствах связи Помпаж. Способы повышения запасов ГДЛУ (борьба с помпажом)
Помпаж. Способы повышения запасов ГДЛУ (борьба с помпажом) Графен – бұл кәдімгі алмаз бен графиттен
Графен – бұл кәдімгі алмаз бен графиттен Презентация на тему Действие электрического тока на тело человека
Презентация на тему Действие электрического тока на тело человека  Напруження і деформації при згині
Напруження і деформації при згині Графическое представление физического процесса - функция
Графическое представление физического процесса - функция Частотные методы синтеза
Частотные методы синтеза Свойства внешнего эвольвентного зацепления
Свойства внешнего эвольвентного зацепления Лекция 1 Ядерно-топливный цикл
Лекция 1 Ядерно-топливный цикл Презентация на тему Специальная теория относительности
Презентация на тему Специальная теория относительности  Ультрафиолетовое излучение
Ультрафиолетовое излучение Измерение скоростей продольных волн в образцах методом прямого просвечивания
Измерение скоростей продольных волн в образцах методом прямого просвечивания Телефон без электричества. Физика
Телефон без электричества. Физика Низкотемпературное гетерогенное разделение и концентрирование
Низкотемпературное гетерогенное разделение и концентрирование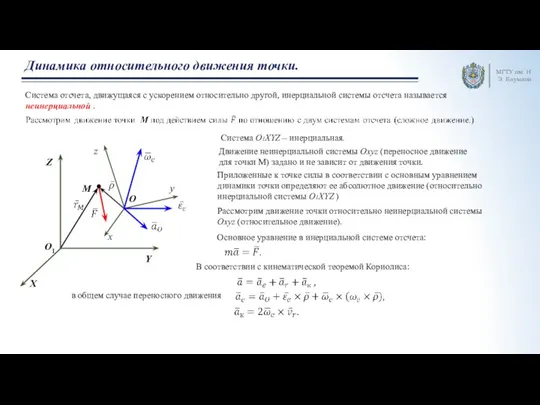 Динамика относительного движения точки. Лекция 2
Динамика относительного движения точки. Лекция 2 Польза и вред электризации
Польза и вред электризации