Содержание
- 2. Выражение примет следующий вид: Отношение количества тепла, полученного системой от какого-либо тела, к температуре этого тела
- 3. Если какая-либо система совершает цикл, в ходе которого вступает в теплообмен с двумя тепловыми резервуарами, температуры
- 4. Если система в ходе цикла вступает в теплообмен не с двумя, а с N телами, причем
- 5. Если в ходе теплообмена с системой температура внешних тел изменяется, то каждый процесс передачи тепла можно
- 6. Знак равенства соответствует обратимому процессу, знак неравенства – необратимому процессу. Для обратимого процесса: В пределе, переходя
- 7. ЭНТРОПИЯ.
- 8. Элементарное приращение энтропии равно элементарному количеству тепла, получаемому системой извне, отнесенному к температуре, при которой это
- 9. В случае необратимого перехода из состояния 1 в состояние 2: Объединим вместе выражения для изменения энтропии
- 10. Если система теплоизолирована (не обменивается теплом с окружающей средой), то:
- 11. Определим изменение энтропии при обратимом переходе из состояния 1 в состояние 2:
- 12. При изотермическом процессе (Т1 = Т2):
- 13. Для того, чтобы найти изменение энтропии при необратимом процессе, нужно рассмотреть какой-либо обратимый процесс, приводящий систему
- 14. ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ.
- 16. Скачать презентацию













 Метрология. Случайные погрешности: статистические методы оценивания
Метрология. Случайные погрешности: статистические методы оценивания Единицы работы электрического тока, применяемые на практике
Единицы работы электрического тока, применяемые на практике Оптические явления
Оптические явления МБОУ «Юхмачинская средняя общеобразовательная школа» Алькеевского муниципального района Республики Татарстан ФИЗИКА В ПРИРОДЕ
МБОУ «Юхмачинская средняя общеобразовательная школа» Алькеевского муниципального района Республики Татарстан ФИЗИКА В ПРИРОДЕ  Презентация на тему Электрическая цепь
Презентация на тему Электрическая цепь  Адиабатическое приближение
Адиабатическое приближение Лётные и эксплуатационные ограничения многодвигательного ВС DA-42. Тема 7
Лётные и эксплуатационные ограничения многодвигательного ВС DA-42. Тема 7 Физика. Физические явления
Физика. Физические явления Динер Никита Физика Инерция
Динер Никита Физика Инерция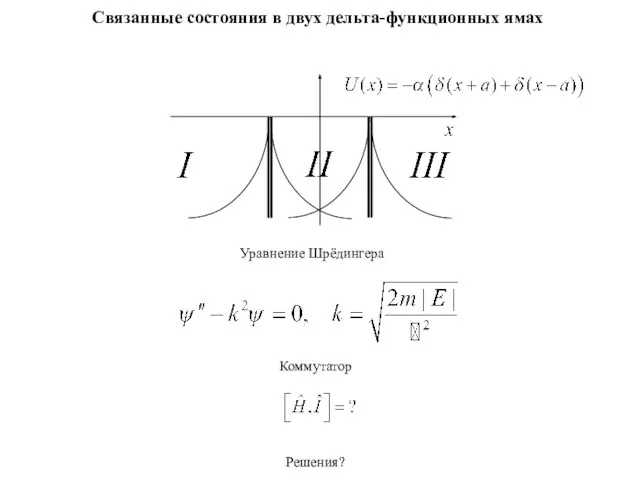 Связанные состояния в двух дельта - функционных ямах
Связанные состояния в двух дельта - функционных ямах Солнце, воздух и вода – наши лучшие друзья
Солнце, воздух и вода – наши лучшие друзья Револьверный станок
Револьверный станок Магнитное поле
Магнитное поле Внутренняя энергия. Работа в термодинамике. Количество теплоты
Внутренняя энергия. Работа в термодинамике. Количество теплоты Иллюзии и Физика. Вечная Борьба
Иллюзии и Физика. Вечная Борьба Теория пластин
Теория пластин Расчёт кругового поворота автомобиля
Расчёт кругового поворота автомобиля Сила трения
Сила трения Презентация на тему Кипение
Презентация на тему Кипение  Интерактивные лабораторные работы по физике
Интерактивные лабораторные работы по физике Нанотехнологии вокруг нас
Нанотехнологии вокруг нас Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила
Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила  Физика и В.О.В
Физика и В.О.В Способы увеличения подачи воздуха и топлива в цилиндры двигателя внутреннего сгорания (ДВС)
Способы увеличения подачи воздуха и топлива в цилиндры двигателя внутреннего сгорания (ДВС)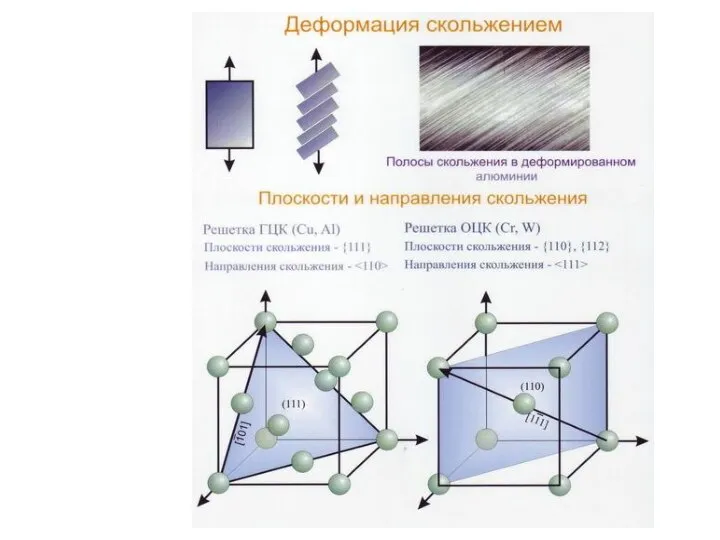 Пластическая деформация металлов
Пластическая деформация металлов ИК-спектроскопия
ИК-спектроскопия Техобслуживание
Техобслуживание Термодинамические системы и термодинамические параметры
Термодинамические системы и термодинамические параметры