Слайд 2Основная задача классической механики - определить положение тела в пространстве в любой

момент времени.
По характеру решаемых задач классическую механику делят на кинематику, динамику и статику.
Слайд 3Кинематика описывает движение тел без выяснения причин, вызывающих данное движение.
Динамика – раздел

механики, в котором изучаются причины движения.
Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел.
Законы сохранения импульса и энергии являются следствиями законов Ньютонов.
Слайд 4Механическим движением тела называется изменение положения тела в пространстве относительно других тел

с течением времени.
Закон относительности движения: характер движения тела зависит от того, относительно каких тел мы рассматриваем движение.
Нет абсолютно неподвижных тел.
Слайд 5Прямолинейное равномерное движение
Описать движение тела – это значит, указать способ определения его

положения в пространстве в любой момент времени.
Для описания движения нужно ввести некоторые понятия: материальная точка, траектория, путь, перемещение, координата, момент времени, промежуток времени, скорость.
Слайд 6Материальная точка - тело, размерами которого в условиях рассматриваемой задачи можно пренебречь.

Тело, движущееся поступательно, можно принимать за материальную точку даже в том случае, если его размеры соизмеримы с проходимыми им расстояниями.
Слайд 7Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые

две точки тела, остается параллельным самому себе.
Слайд 8Что нужно знать для того, чтобы указать положение тела?
Во-первых, знать, где

оно было в начальный момент времени; во-вторых, каков вектор перемещения в любой момент времени.
Тело, относительно которого рассматривается движение, называется телом отсчета.
Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Слайд 9Два способа описания движения тел
Координатный
Векторный
В координатном способе положение тела в пространстве задается координатами,

которые с течением времени меняются.
Слайд 10В векторном способе используется радиус-вектор.
Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную

точку. Закон (или уравнение) движения в векторной форме - зависимость радиуса-вектора от времени:
Слайд 11Для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости

всех трех ее координат от времени, либо зависимость от времени радиус-вектора этой точки.
Три скалярных уравнения или эквивалентное им одно векторное уравнение называются кинематическими уравнениями движения материальной точки.
Слайд 12Двигаясь, материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета.

Линия, по которой движется точка в пространстве, называется траекторией.
По форме траектории все движения делятся на прямолинейные и криволинейные.
Слайд 13Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём,

пройденным за этот промежуток времени. Его обозначают буквой S.
Путь – скалярная величина.
Слайд 14Для описания движения тела нужно указать, как меняется положение точек с течением

времени.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Обозначается на чертежах как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:
Слайд 15Важной величиной, характеризующей движение тела, является его скорость. Скорость – векторная величина.

Она считается заданной, если известен ее модуль и направление. Скорость равномерного прямолинейного движения точки – векторная величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
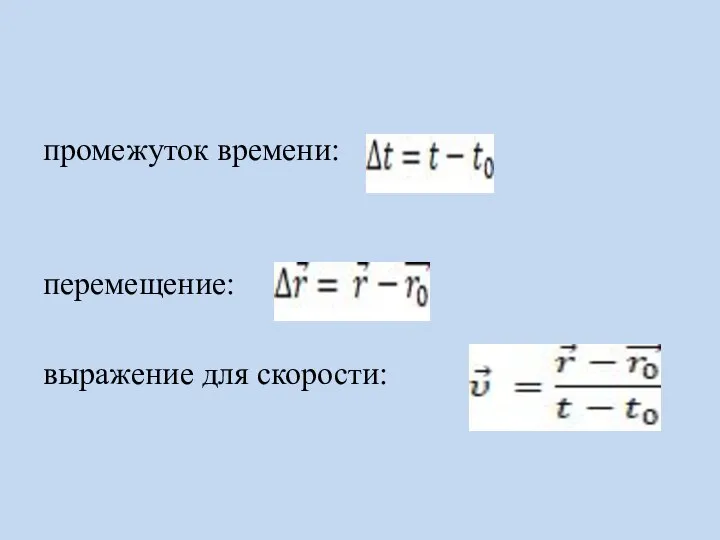
Слайд 16промежуток времени:
перемещение:
выражение для скорости:
Слайд 17Выразим отсюда радиус-вектор:
Это уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор

точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени.
Слайд 18В проекциях на ось ОХ уравнение можно записать в виде: х=х0+vхt.
Это уравнение равномерного

прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х0.
Слайд 19Путь S, пройденный точкой при движении вдоль оси ОХ, равен модулю изменения

ее координаты:
Его можно найти, зная модуль скорости:
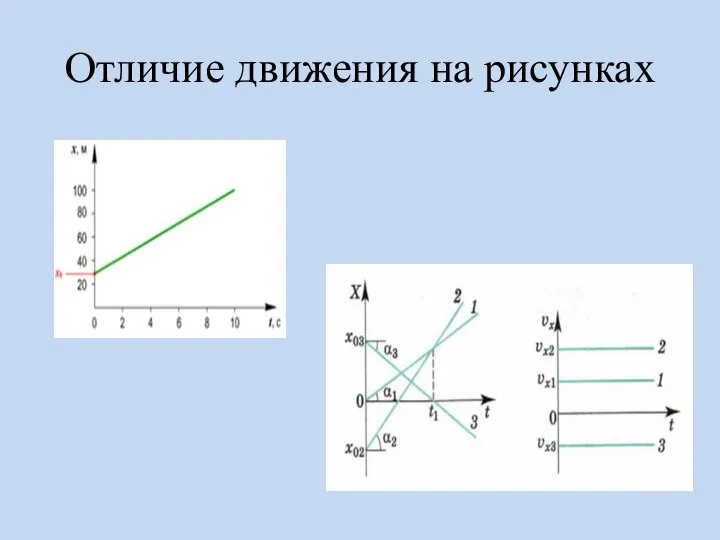
Слайд 21Проекция скорости определяет угол наклона прямой х(t) к оси t и численно

равна тангенсу угла:
Слайд 22Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения

и скорости от выбора системы отсчёта.
В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
Слайд 23Задача 1.
Тело движется равномерно и прямолинейно в положительном направлении оси ОХ. Координата

тела в начальный момент времени равна xо = -10м. Найдите координату тела через 5с, если модуль её скорости равен ʋ=2 м/с. Какой путь проделало тело за это время?
Слайд 24Решение:
Координату точки найдем по формуле:
х = х0 + ?х t
Так как направление вектора скорости

совпадает с направлением оси координат, проекция вектора скорости положительна и равна ʋx=ʋ; тогда вычисляем:
х = - 10 + 2· 5 = 0 (м).
Пройденный путь найдем s = ʋ t; s = 2·5 = 10 м.
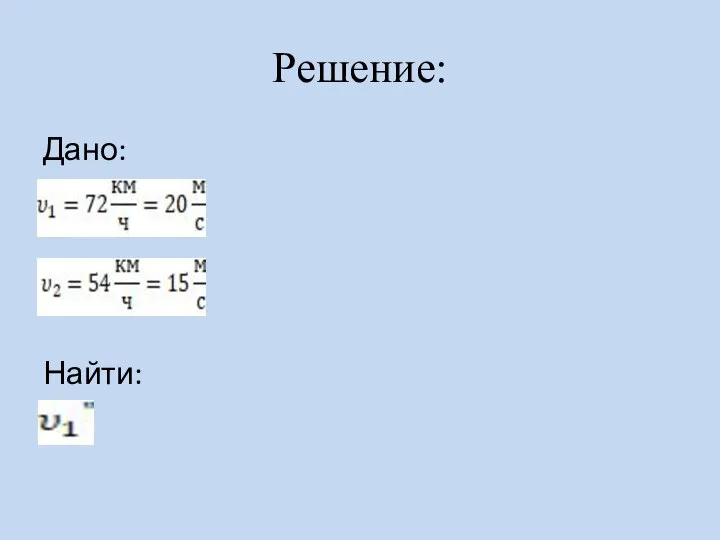
Слайд 25Задача 2
Равномерно друг за другом движутся два поезда. Скорость первого равна 72

км/ч, а скорость второго — 54 км/ч. Определите скорость первого поезда относительно второго.
























 Статическое электричество. Вред и польза для человека. 2 класс
Статическое электричество. Вред и польза для человека. 2 класс Инструмент MATE
Инструмент MATE Диполь. Поле системы зарядов. Теорема Ирншоу
Диполь. Поле системы зарядов. Теорема Ирншоу Исследование цепей с последовательным и параллельным соединением резисторов
Исследование цепей с последовательным и параллельным соединением резисторов Неделя нанотехнологий
Неделя нанотехнологий Второй закон Ньютона
Второй закон Ньютона Электрический ток в газах
Электрический ток в газах Единицы измерения скорости. Формула скорости
Единицы измерения скорости. Формула скорости Цепные ядерные реакции.
Цепные ядерные реакции. 2_mekhanicheskoe_dvizhenie
2_mekhanicheskoe_dvizhenie Автотрансформаторы
Автотрансформаторы Презентация на тему Тепловые машины и их КПД
Презентация на тему Тепловые машины и их КПД  Волны. Интерференция и дифракция
Волны. Интерференция и дифракция АЭС с реактором РБМК
АЭС с реактором РБМК Презентация на тему Величины, характеризующие колебательные движения
Презентация на тему Величины, характеризующие колебательные движения  Презентация на тему Сила трения скольжения
Презентация на тему Сила трения скольжения  Заряды. Закон Кулона
Заряды. Закон Кулона Пирог, сотовая структура Вселенной
Пирог, сотовая структура Вселенной Аппараты для исследования дальнего космоса. Тема № 3
Аппараты для исследования дальнего космоса. Тема № 3 Установка батарей своими руками
Установка батарей своими руками Волны в океане
Волны в океане Оптимальное проектирование диска компрессора
Оптимальное проектирование диска компрессора Радиационный контроль
Радиационный контроль Конденсатор в переменном токе
Конденсатор в переменном токе Решение задач по теме Термодинамика. Теплообмен. Первое начало термодинамики. Тепловые двигатели
Решение задач по теме Термодинамика. Теплообмен. Первое начало термодинамики. Тепловые двигатели 680-сильная Toyota Camry
680-сильная Toyota Camry Металлы в нашей жизни
Металлы в нашей жизни Определение непотопляемости судна
Определение непотопляемости судна