Слайд 2Экспоненциалды тарату заңы
F(t)=1- e-λt; (3.1)
f(t)= λ* e-λt; (3.2)
P(t) = e-λt; (3.3)
Q(t1)= 1

- e-λt; (3.4)
P(t1) = e-λt; (3.5)
Слайд 3Экспоненциалды тарату заңы
∞
τ=∫ P(t)dt =1/λ; (3.6)
0
D[T]=1/λ2; (3.7)
λ(t) = f(t)/P(t) =
![Экспоненциалды тарату заңы ∞ τ=∫ P(t)dt =1/λ; (3.6) 0 D[T]=1/λ2; (3.7) λ(t)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/913827/slide-2.jpg)
λ; (3.8)
Слайд 4Экспоненциалды тарату заңы
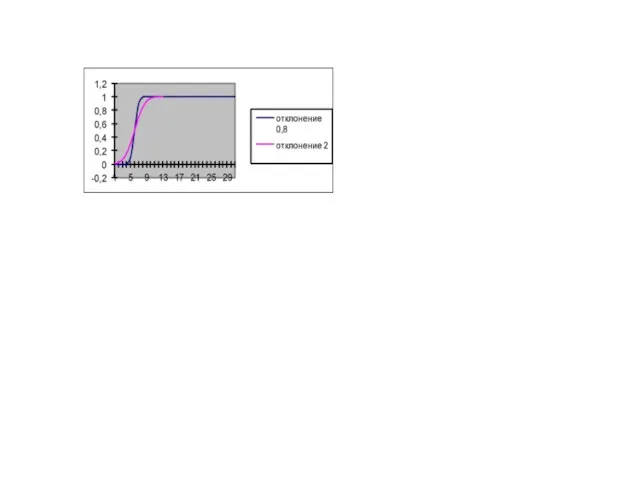
Свойства экспонециального распределения:
1. При λ*t<<1, т.е. t<τ=1/λ
P(t) = 1 -

λ*t =1 – t/τ
с погрешнотью δ<= 0,5*(λ*t)2;
2. P(t1,t3)= e-λt1/ e-λt2= e-λ(t1-t2)
Слайд 5Нормальное распределение:
F(t)=(1/(σ*√2*π )∫ e-(x-m)2/(2*σ)dx ;
f(t)= (1/(σ*√2*π ) *e-(t-m)2/(2*σ2);
τ=m;
D[T]=σ2;
![Нормальное распределение: F(t)=(1/(σ*√2*π )∫ e-(x-m)2/(2*σ)dx ; f(t)= (1/(σ*√2*π ) *e-(t-m)2/(2*σ2); τ=m; D[T]=σ2;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/913827/slide-4.jpg)
Слайд 7
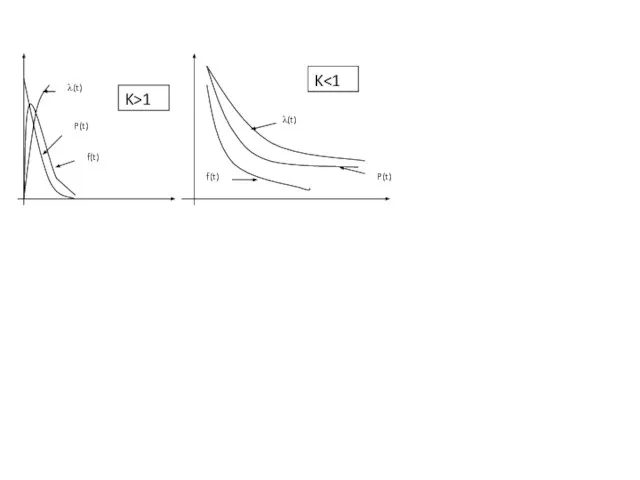
Распределение Вейбулла – Гнеденко.
F(t)=(1/(σ*√2*π )∫ e-(x-m)2/(2*σ)dx ;
f(t)= (1/(σ*√2*π ) *e-(t-m)2/(2*σ2);
F(t)=1- e-αtk

;
f(t)= α*t(k-1)*k*e-αtk;
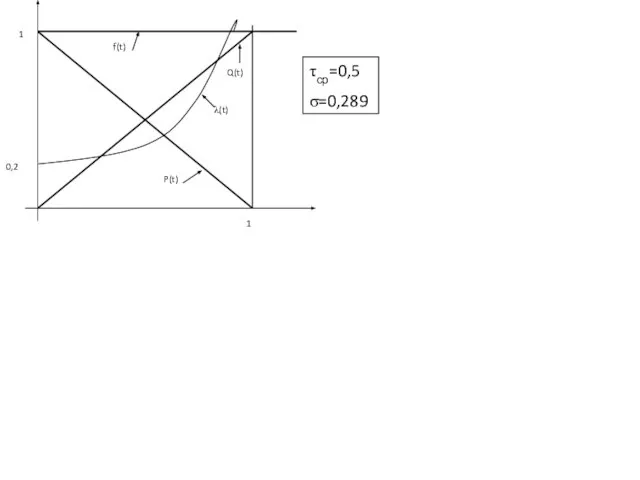
Слайд 9Равномерный закон:
f при 0 < t < 1/f
f(t) = 0 при t

> 1/f
P(t) = 1 – f*t;
f/(1-f*t) 0 < t < 1/f
λ(t) = 0 t > 1/f
∞ 1/a
τср= ∫(1- f*t)dt= ∫ (1-f*t)dt = 1/(2*a);
0 0
∞ 1/a
D(t)=∫ (t-τср)2*f(t)dt =∫ (1-1/(2*a))2f(t)dt =1/(12*a2);
0 0
σ(t) = √ (1-1/(12*a2) = 1/(2*a*√3 );
h(t)=f* e ft;

![Экспоненциалды тарату заңы ∞ τ=∫ P(t)dt =1/λ; (3.6) 0 D[T]=1/λ2; (3.7) λ(t)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/913827/slide-2.jpg)

![Нормальное распределение: F(t)=(1/(σ*√2*π )∫ e-(x-m)2/(2*σ)dx ; f(t)= (1/(σ*√2*π ) *e-(t-m)2/(2*σ2); τ=m; D[T]=σ2;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/913827/slide-4.jpg)


 Лабораторная работа. Измерение удельной теплоемкости твердого тела
Лабораторная работа. Измерение удельной теплоемкости твердого тела Динамика точки. Законы Галилея – Ньютона
Динамика точки. Законы Галилея – Ньютона Презентация на тему Типы интегральных схем
Презентация на тему Типы интегральных схем  Курс лекций по теоретической механике. Статика
Курс лекций по теоретической механике. Статика ИСПАР И КОНДЕН
ИСПАР И КОНДЕН Что такое электричество
Что такое электричество Ременные передачи
Ременные передачи Автомобили III
Автомобили III Изготовление и изучение дифракционных оптических элементов
Изготовление и изучение дифракционных оптических элементов 679405
679405 Физика древесины
Физика древесины Общие теоремы динамики
Общие теоремы динамики Физика в игрушках
Физика в игрушках Лесозаготовительная техника
Лесозаготовительная техника Элементы теории относительности
Элементы теории относительности Собственный механический и магнитный моменты электрона. Спин
Собственный механический и магнитный моменты электрона. Спин лекция 2 Динамика. Сила. Работа. Энергия. Импульс. (2)
лекция 2 Динамика. Сила. Работа. Энергия. Импульс. (2) Tlak v kvapalinách
Tlak v kvapalinách Введение в оптоэлектронику
Введение в оптоэлектронику Исследовать зависимость дальности полёта снаряда от угла вылета
Исследовать зависимость дальности полёта снаряда от угла вылета Внутренняя энергия и способы её изменения
Внутренняя энергия и способы её изменения Электроэнергетические системы и сети. Определение параметров элементов электрической сети
Электроэнергетические системы и сети. Определение параметров элементов электрической сети Абсолютные и относительные величины
Абсолютные и относительные величины Сверхпроводимость. Свойства
Сверхпроводимость. Свойства Презентация по физике "Атомная энергетика" -
Презентация по физике "Атомная энергетика" -  Электрическое сопротивление проводников. Единицы сопротивления. Закон Ома для участка цепи
Электрическое сопротивление проводников. Единицы сопротивления. Закон Ома для участка цепи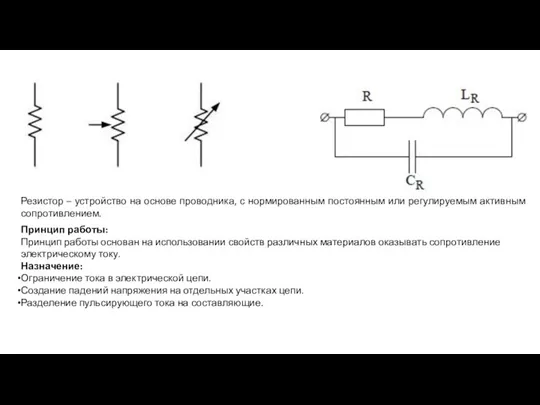 Радиоэлементы. Принцип работы
Радиоэлементы. Принцип работы Магнитные явления
Магнитные явления