Слайд 5Дифракция на круглом отверстии

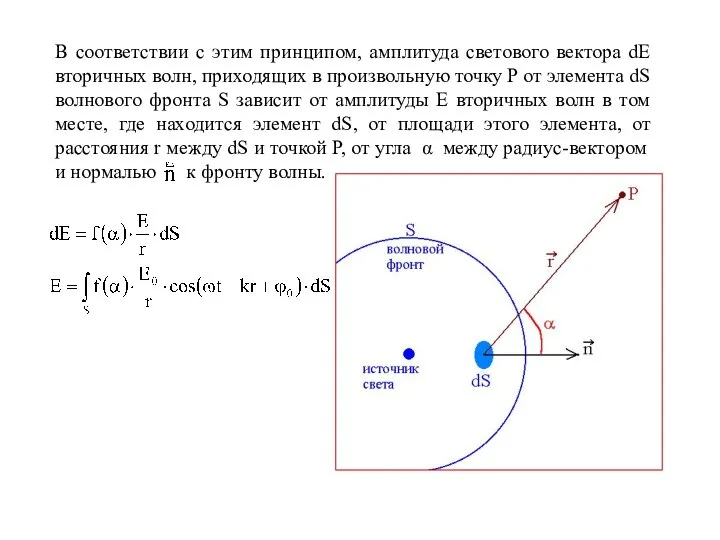
Слайд 9Решение задач по расчету дифракционной картины основывается на принципе Гюйгенса-Френеля:
Каждая частица среды,

до которой дошла световая волна, сама становится источником вторичных когерентных волн, результат интерференции которых определяет положение фронта волны в каждый следующий момент времени.
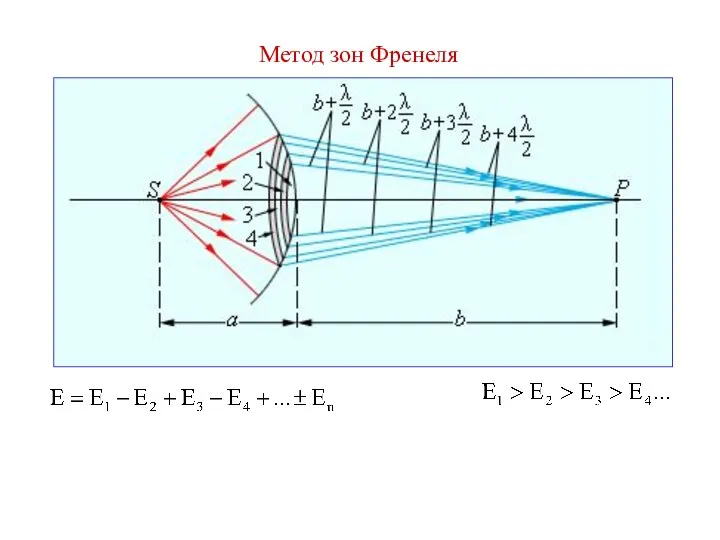
Слайд 15«+» : n - нечетное
«-» : n - четное

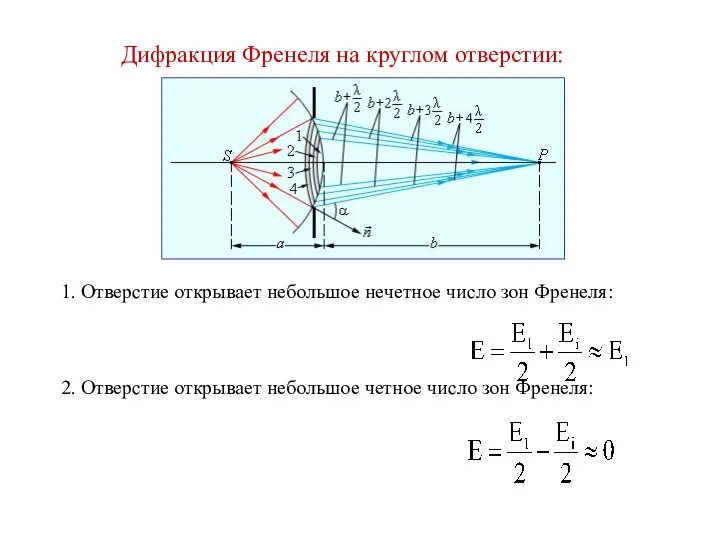
Слайд 16Дифракция Френеля на круглом отверстии:
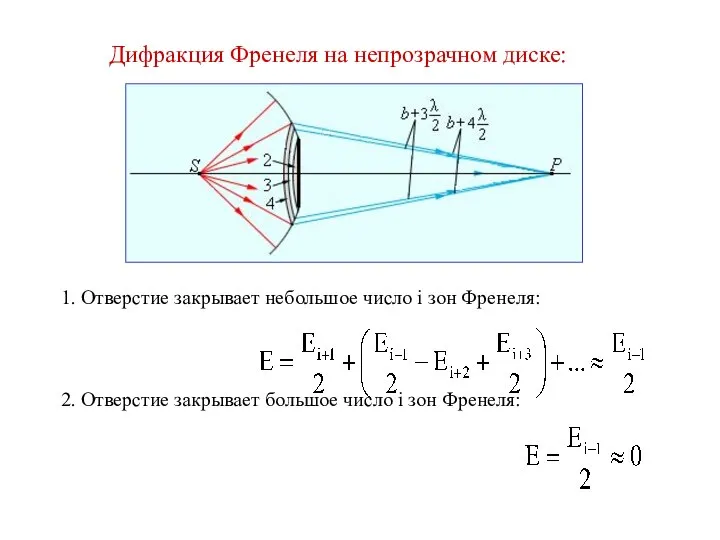
Слайд 17Дифракция Френеля на непрозрачном диске:
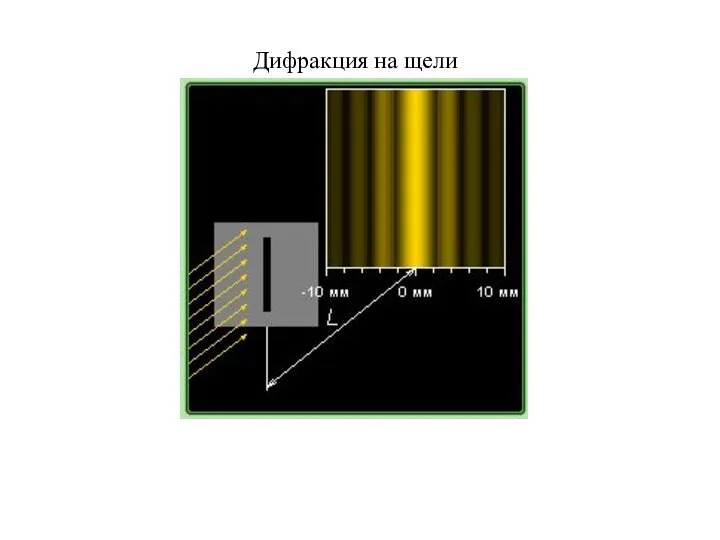
Слайд 18Условие максимума для щели
Условие минимума для щели

Слайд 19Условие максимума для дифракционной решетки
Условие минимума для дифракционной решетки





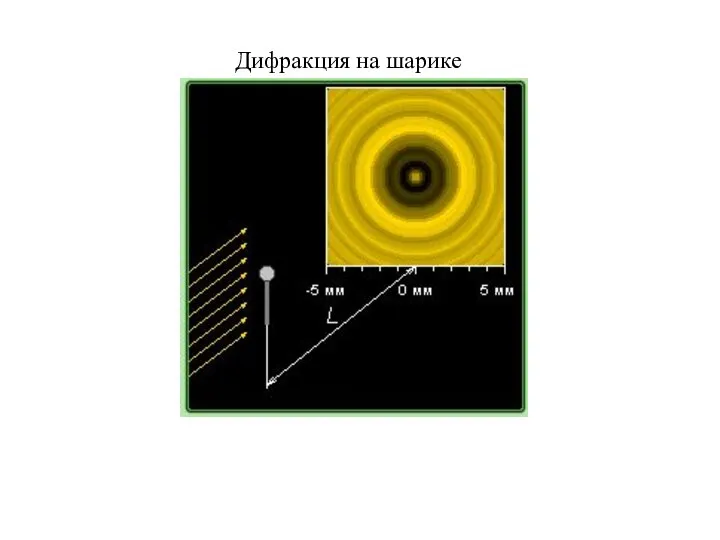
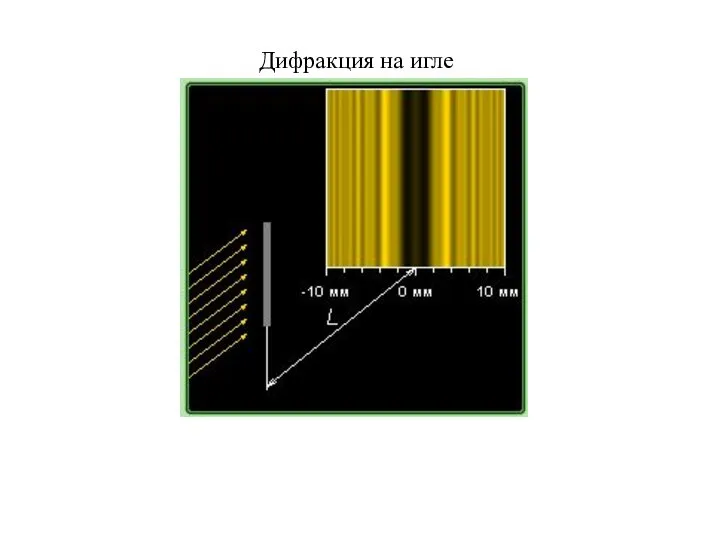








 Давление
Давление Сила упругости
Сила упругости Контрольная работа по теме МКТ
Контрольная работа по теме МКТ Презентация на тему Никола Тесла (1856-1943)
Презентация на тему Никола Тесла (1856-1943)  Свойства жидкостей. Поверхностное натяжение
Свойства жидкостей. Поверхностное натяжение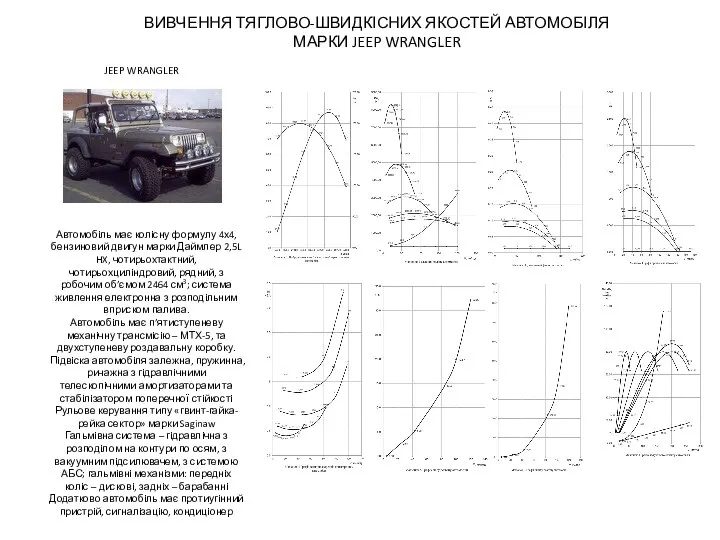 Вивчення тяглово-швидкісних якостей автомобіля марки Jeep Wrangler
Вивчення тяглово-швидкісних якостей автомобіля марки Jeep Wrangler Урок-сказка: Первоначальные сведения о строении вещества 7 класс
Урок-сказка: Первоначальные сведения о строении вещества 7 класс Второй закон термодинамики
Второй закон термодинамики Теплоемкость. Уравнение теплового баланса
Теплоемкость. Уравнение теплового баланса Электрическое_поле_в_вакууме_лекция
Электрическое_поле_в_вакууме_лекция Контрольная передачи
Контрольная передачи Кот Шрёдингера. Коллапс волновой функции. Введение в квантовую физику
Кот Шрёдингера. Коллапс волновой функции. Введение в квантовую физику Неразъемные соединения
Неразъемные соединения Гармонические колебания
Гармонические колебания Использование УМК Живая физика в проектной деятельности учащихся
Использование УМК Живая физика в проектной деятельности учащихся Кожухотрубный реактор
Кожухотрубный реактор Сообщающиеся сосуды
Сообщающиеся сосуды Место доказательств в научном познании
Место доказательств в научном познании Испарение. Насыщенный и ненасыщенный пар
Испарение. Насыщенный и ненасыщенный пар Моделирование электромагнитных волн в цилиндрическом волноводе
Моделирование электромагнитных волн в цилиндрическом волноводе Электрический ток в вакууме
Электрический ток в вакууме Единицы работы электрического тока, применяемые на практике
Единицы работы электрического тока, применяемые на практике Сборка, регулировка и испытание охлаждения и смазки двигателей
Сборка, регулировка и испытание охлаждения и смазки двигателей Наноматериалы, нанотехнологии в области технического обслуживания и ремонта транспортных средств
Наноматериалы, нанотехнологии в области технического обслуживания и ремонта транспортных средств Силы в механике. Импульс тела. Закон сохранения
Силы в механике. Импульс тела. Закон сохранения Использование интернет – технологий в обучении физики
Использование интернет – технологий в обучении физики Сравнение КАМАЗ-5490 NEO и КАМАЗ-54901
Сравнение КАМАЗ-5490 NEO и КАМАЗ-54901 Презентация_Sintecon_хроматография_краткая_обо_всем
Презентация_Sintecon_хроматография_краткая_обо_всем