Содержание
- 2. Сопротивление материалов – наука о прочности и деформируемости элементов (деталей) сооружений и машин
- 3. Литература 1. Ицкович Г.М. Сопротивление материалов. 2. Феодосьев В.И. Сопротивление материалов. 3. Петрухин Г.Г. Сопротивление материалов.
- 4. Задачи сопротивления материалов Первая задача - расчет элементов конструкций на прочность. Прочность - способность детали сопротивляться
- 5. Задачи сопротивления материалов Вторая задача - расчет элементов конструкций на жесткость Жесткость - способность материала или
- 6. Задачи сопротивления материалов Третья задача - расчет элементов конструкций на устойчивость
- 7. Классификация сил Внешние силы: активные (нагрузки) и реактивные (реакции связей). Объемные силы – силы, действующие на
- 8. Классификация сил По характеру изменения во времени различают: - статические нагрузки, нарастающие медленно и плавно от
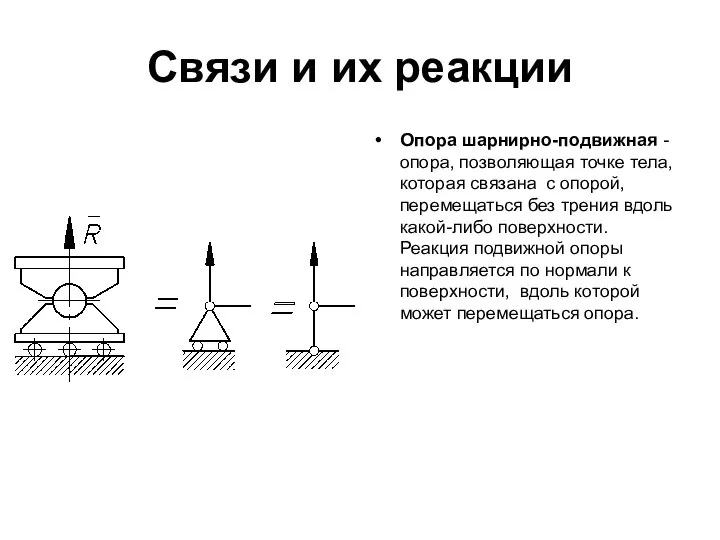
- 9. Связи и их реакции Опора шарнирно-подвижная - опора, позволяющая точке тела, которая связана с опорой, перемещаться
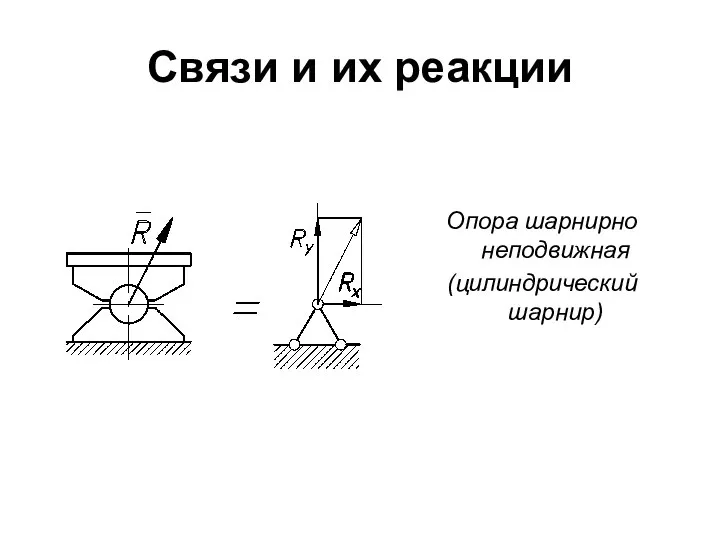
- 10. Связи и их реакции Опора шарнирно неподвижная (цилиндрический шарнир)
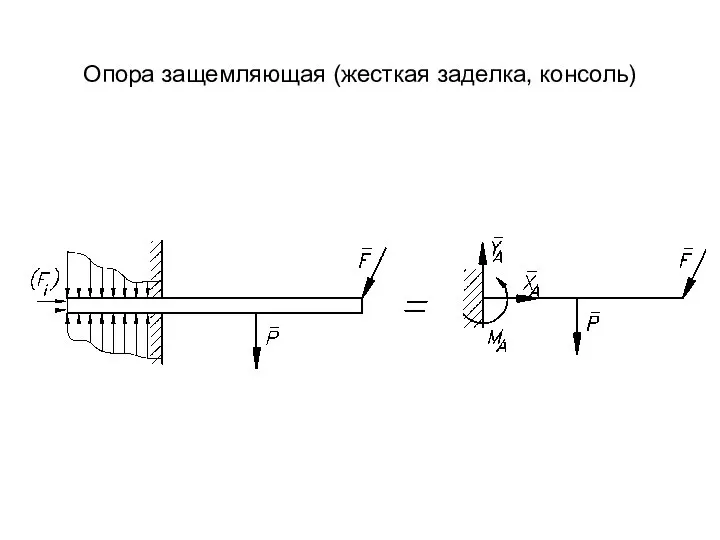
- 11. Опора защемляющая (жесткая заделка, консоль)
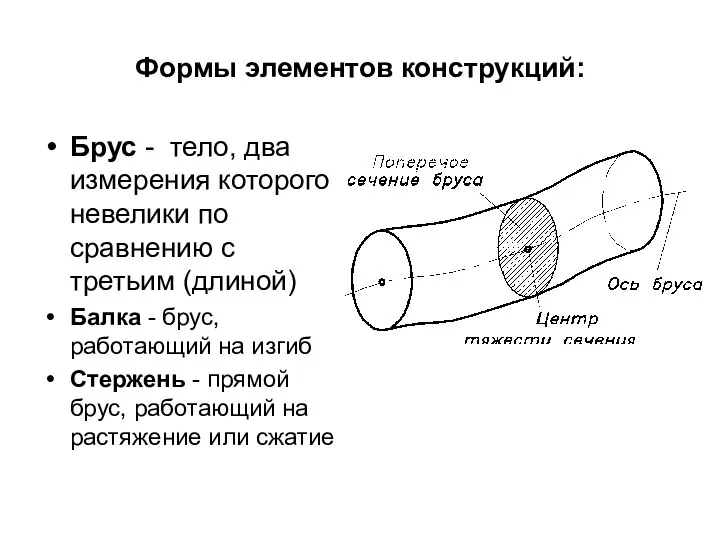
- 12. Формы элементов конструкций: Брус - тело, два измерения которого невелики по сравнению с третьим (длиной) Балка
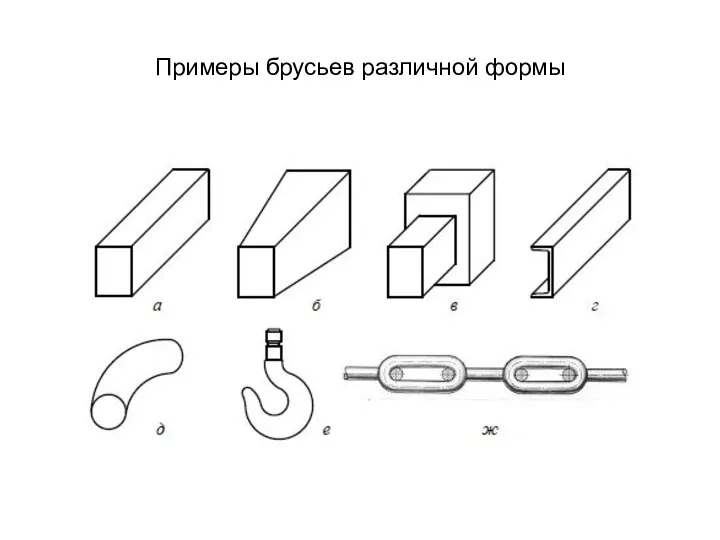
- 13. Примеры брусьев различной формы
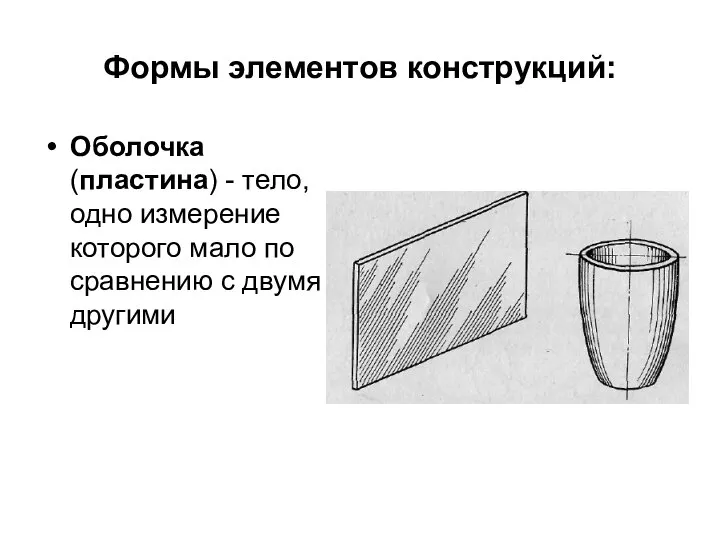
- 14. Формы элементов конструкций: Оболочка (пластина) - тело, одно измерение которого мало по сравнению с двумя другими
- 15. Массив тело, все три измерения которого - величины одного порядка (строительный блок, шарик или ролик подшипника
- 16. ГИПОТЕЗЫ И ДОПУЩЕНИЯ, ПРИНЯТЫЕ В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
- 17. Материал однороден, т. е. свойства любых сколь угодно малых его частиц совершенно тождественны. Это допущение достаточно
- 18. 2. Тело рассматривается как сплошная среда, т.е. материал полностью заполняет весь объем тела без каких-либо пустот.
- 19. Материал изотропен, т.е. физико-механические свойства его по всем направлениям одинаковы. Материалы, не обладающие указанным свойством, называют
- 20. В известных пределах нагружения материал обладает идеальной упругостью, т.е. после снятия нагрузки деформации полностью исчезают
- 21. 5. Перемещения точек упругого тела в известных пределах нагружения прямо пропорциональны силам, вызывающим эти перемещения. «Ut
- 22. Роберт Гук 1635–1703
- 23. 6. Гипотеза Бернулли о плоских сечениях – поперечные сечения, плоские и нормальные к оси стержня до
- 24. 7. Принцип Сен-Венана – в сечениях, достаточно удаленных от мест приложения нагрузки, деформация тела не зависит
- 25. Адемар Жан-Клод Барре де СЕН-ВЕНАН (1797 - 1886)
- 27. 8. Принцип независимости действия сил (принцип суперпозиции)- результат воздействия нескольких внешних факторов равен сумме результатов воздействия
- 28. 9. Принцип начальных размеров (гипотеза о малости деформаций) – деформации в точках тела настолько малы по
- 29. Внутренние силовые факторы
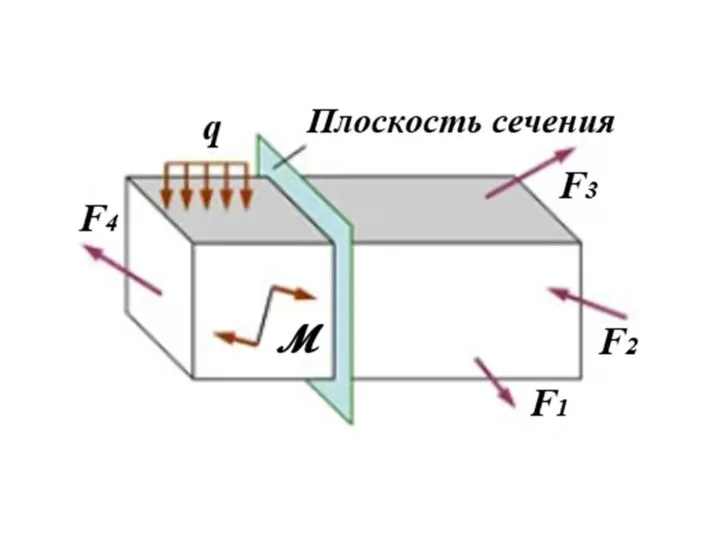
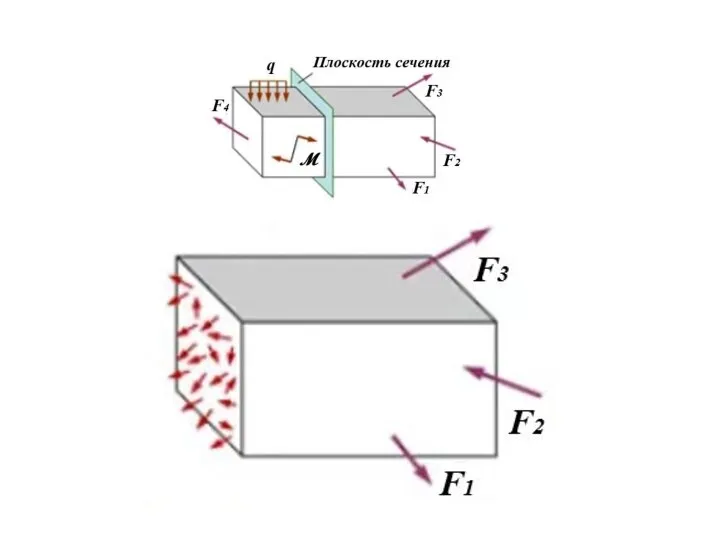
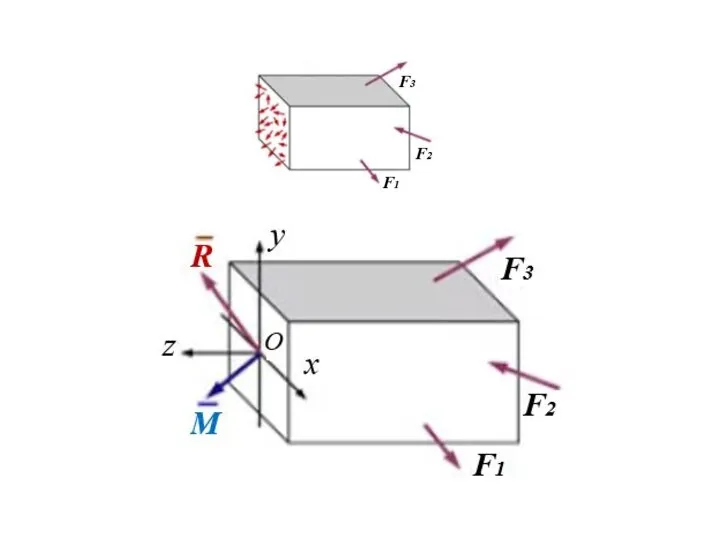
- 30. Метод сечений - определение внутренних усилий путем составления уравнений равновесия любой отсеченной части тела
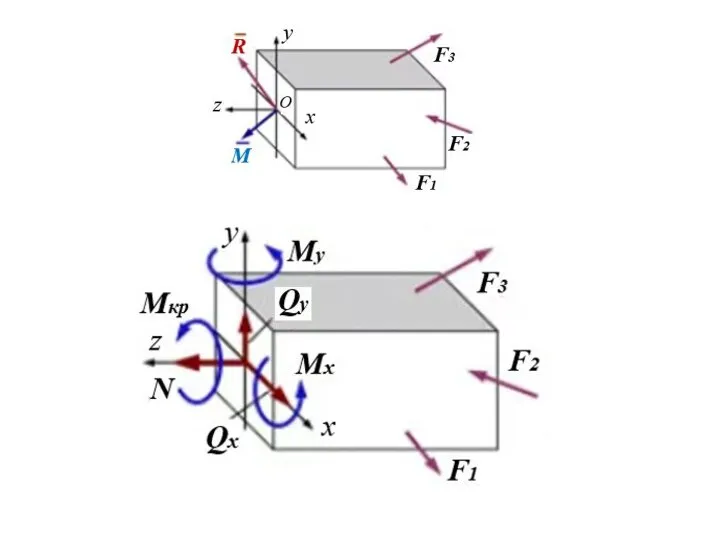
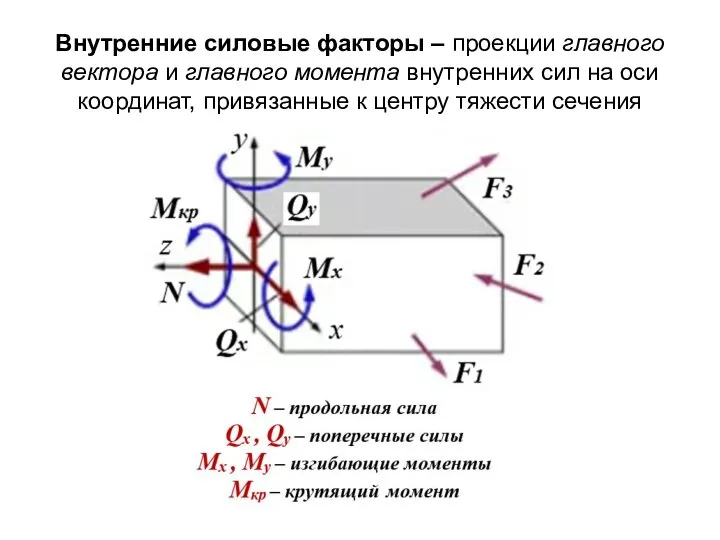
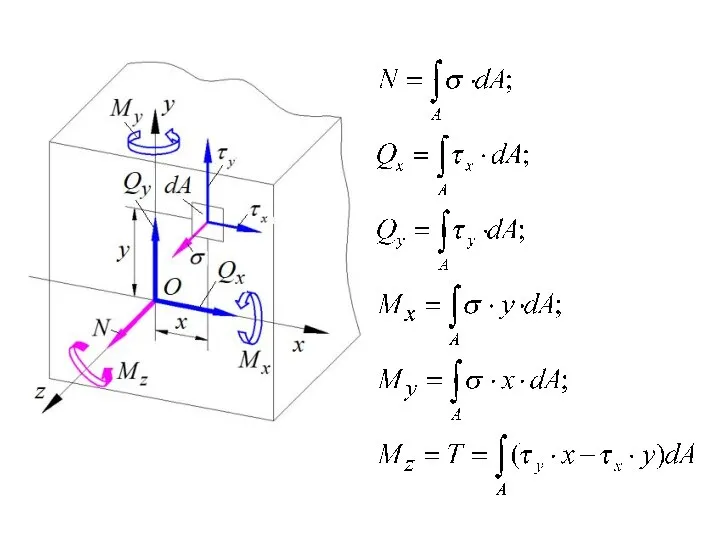
- 35. Внутренние силовые факторы – проекции главного вектора и главного момента внутренних сил на оси координат, привязанные
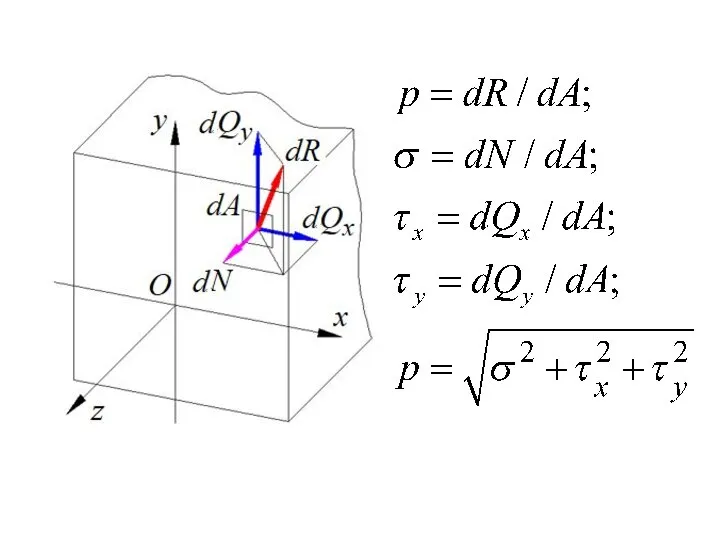
- 36. Напряжения Напряжение механическое полное – мера интенсивности распределения внутренних сил. Для любой точки А упругого тела
- 37. Огюстен Луи Коши 1789 - 1857
- 40. Растяжение (сжатие) – вид деформации, при котором из шести внутренних силовых факторов не равно нулю одно
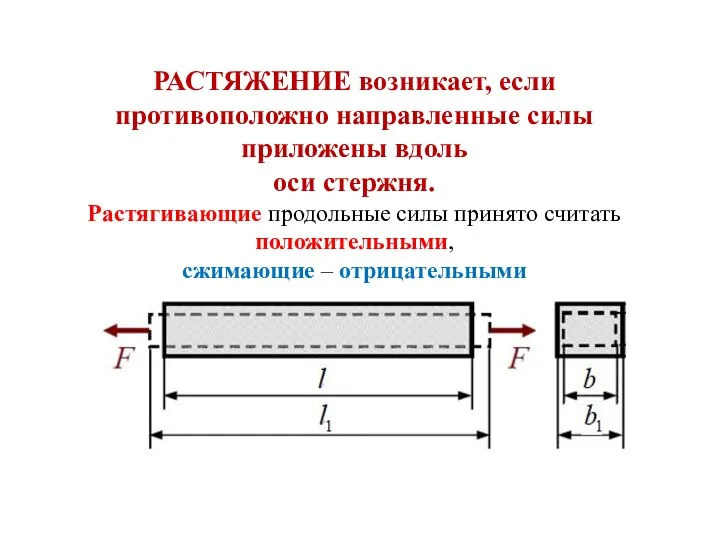
- 41. РАСТЯЖЕНИЕ возникает, если противоположно направленные силы приложены вдоль оси стержня. Растягивающие продольные силы принято считать положительными,
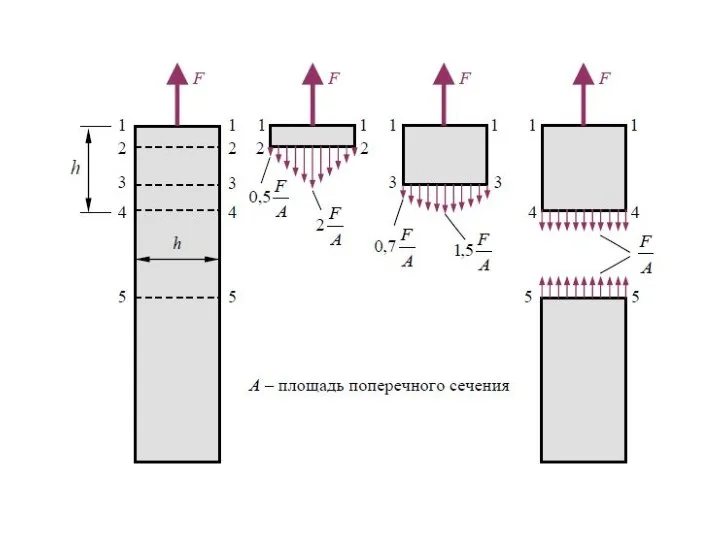
- 42. Напряжения в поперечных сечениях бруса При растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные
- 43. Деформации при растяжении и сжатии Закон Гука
- 44. Современное определение модуля Юнга было дано в 1826 г. за три года до смерти Юнга французским
- 45. Томас Юнг (Янг) (1773-1829) английский физик, механик, врач, астроном и востоковед, один из создателей волновой теории
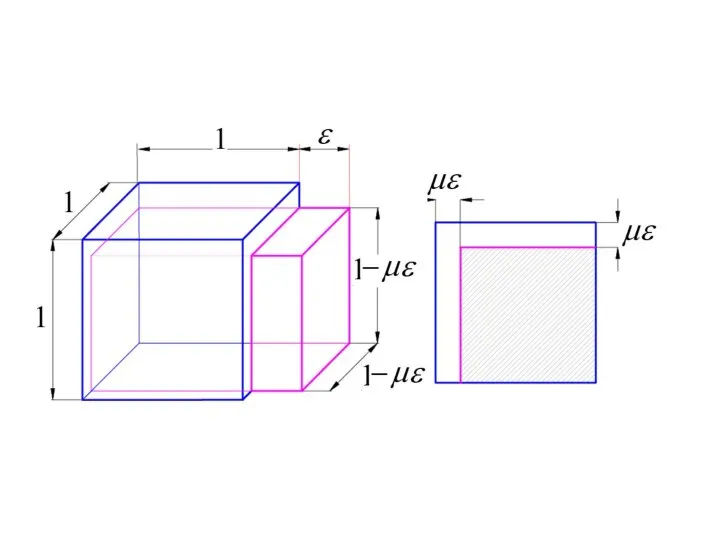
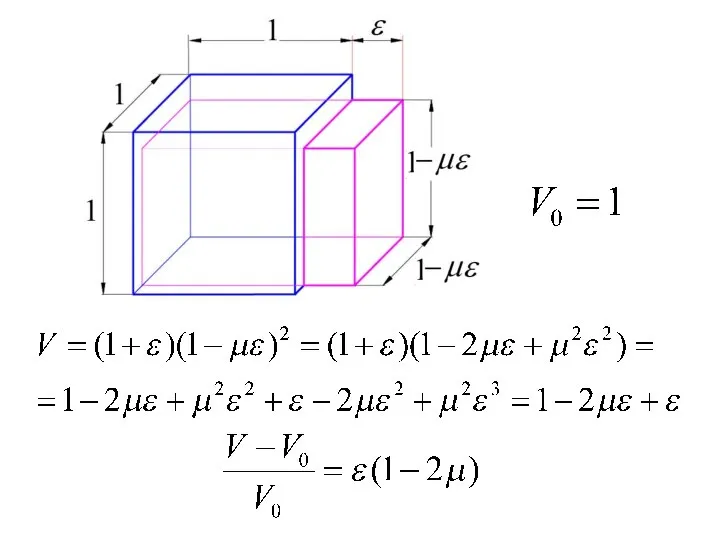
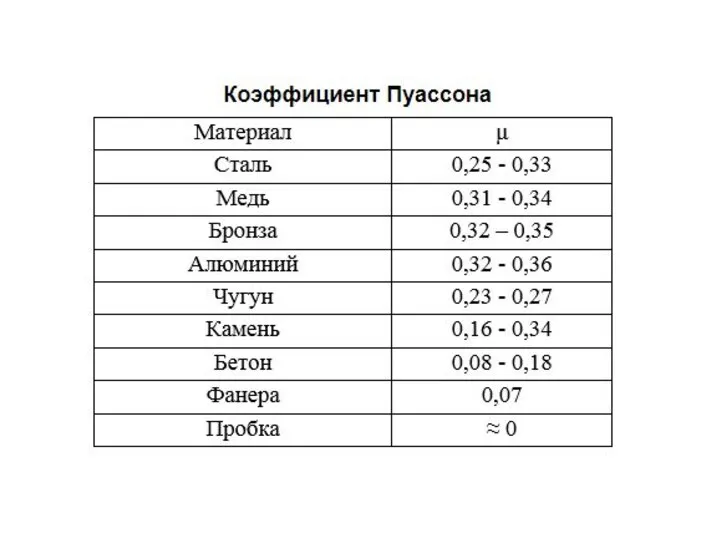
- 46. Коэффициент Пуассона
- 47. Симеон Дени ПУАССОН (1781-1840)
- 48. Как показывает опыт, при растяжении бруска длина его увеличивается на величину Δl, ширина же уменьшается на
- 52. Деформации стержня при растяжении-сжатии
- 56. Энергия деформации при растяжении
- 57. Теорема Клапейрона «Работа силы, статически приложенной к линейно-деформируемой системе, равна половине произведения конечного значения силы на
- 58. Суммируя по всей длине стержня, определяем Для всей системы
- 59. Для стержня (участка стержня) постоянного поперечного сечения при условии, что продольная сила по длине стержня не
- 60. Бенуа Поль Эмиль КЛАПЕЙРОН (1799-1864)
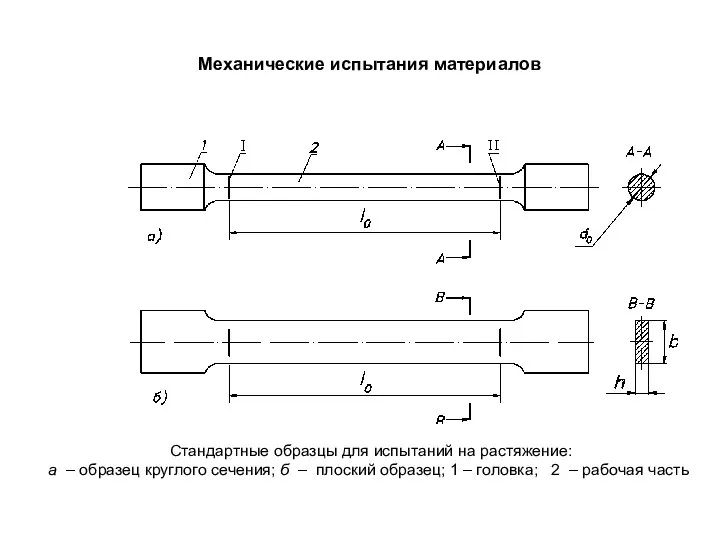
- 61. Механические испытания материалов Стандартные образцы для испытаний на растяжение: а – образец круглого сечения; б –
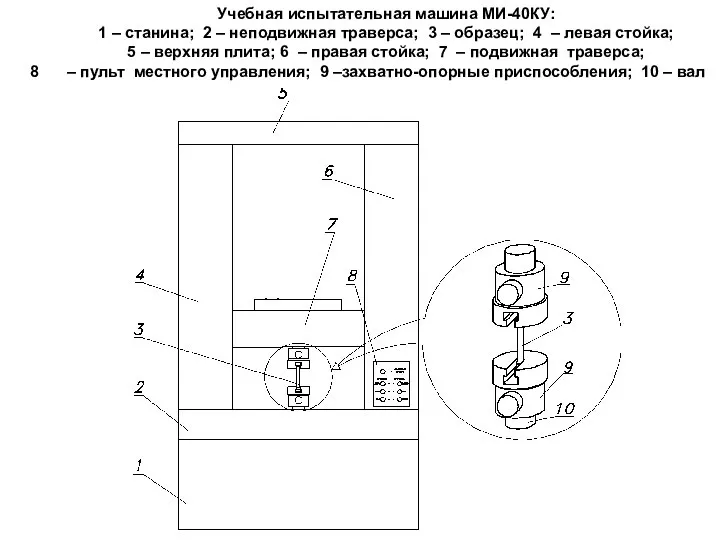
- 62. Учебная испытательная машина МИ-40КУ: 1 – станина; 2 – неподвижная траверса; 3 – образец; 4 –
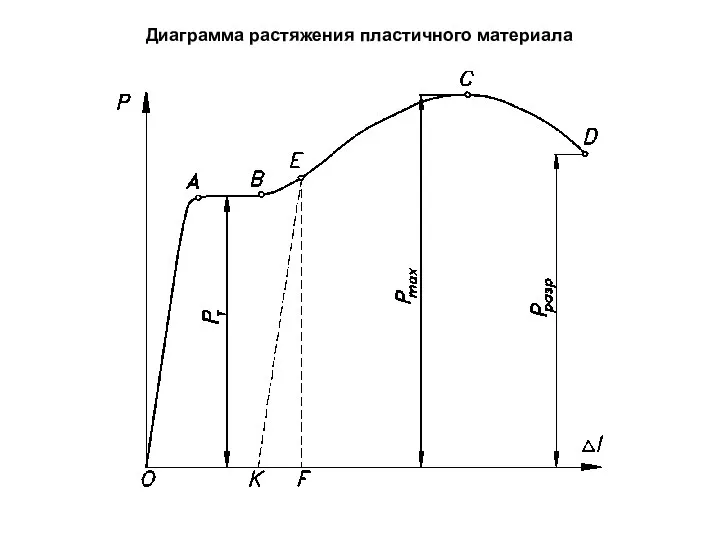
- 63. Диаграмма растяжения пластичного материала
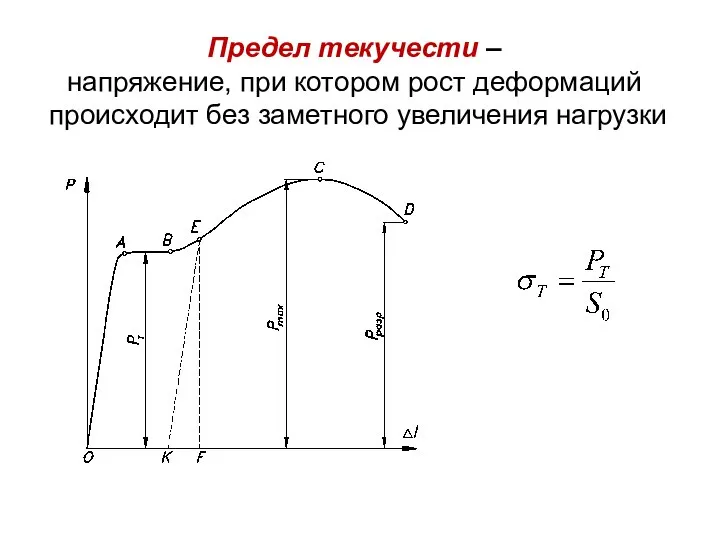
- 64. Предел текучести – напряжение, при котором рост деформаций происходит без заметного увеличения нагрузки
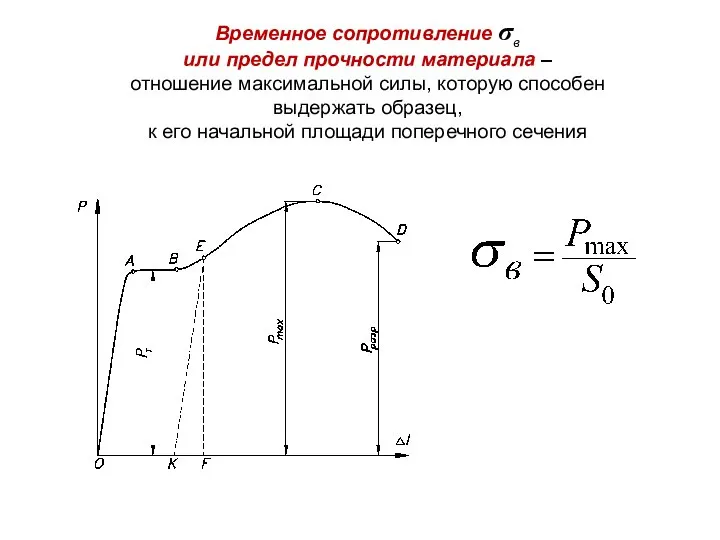
- 65. Временное сопротивление σв или предел прочности материала – отношение максимальной силы, которую способен выдержать образец, к
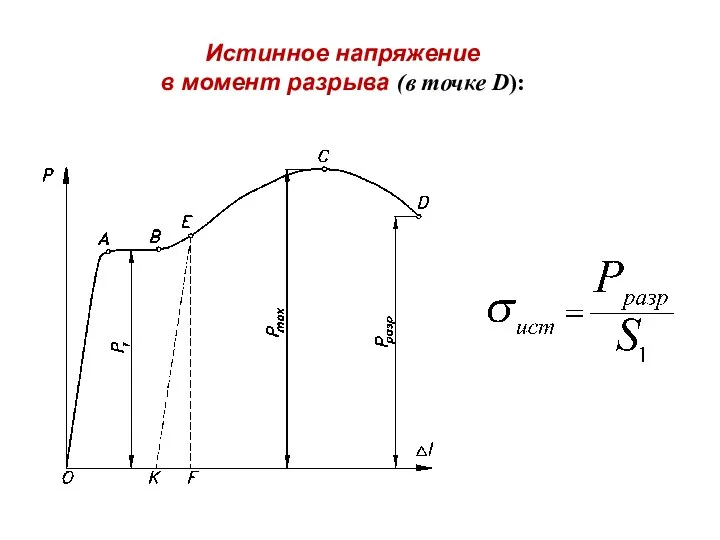
- 66. Истинное напряжение в момент разрыва (в точке D):
- 68. Скачать презентацию









































 Турнир юных знатоков физики
Турнир юных знатоков физики Уравнение Эйлера
Уравнение Эйлера Определение коэффициента силы трения
Определение коэффициента силы трения Закон вращательного движения абсолютно твердого тела. Гироскоп
Закон вращательного движения абсолютно твердого тела. Гироскоп Звуковые волны
Звуковые волны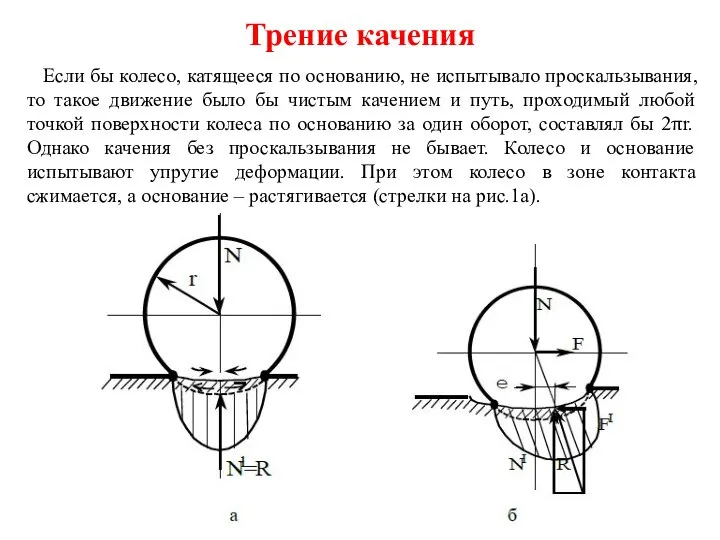 Трение качения
Трение качения Использование интернет – технологий в обучении физики
Использование интернет – технологий в обучении физики Магнитное поле. Лекция 19. Закон Био-Савара-Лапласа. Теорема о циркуляции вектора магнитной индукции
Магнитное поле. Лекция 19. Закон Био-Савара-Лапласа. Теорема о циркуляции вектора магнитной индукции Бином Ньютона. 11 класс
Бином Ньютона. 11 класс Термодинамика. Внутренняя энергия
Термодинамика. Внутренняя энергия 16M33┐є┐и▓ё╙═╗·┐к╖в┼р╤╡╫╩┴╧пер
16M33┐є┐и▓ё╙═╗·┐к╖в┼р╤╡╫╩┴╧пер Презентация на тему Давление твёрдых тел
Презентация на тему Давление твёрдых тел  Решение задач МКТ
Решение задач МКТ Явления тяготения. Сила тяжести
Явления тяготения. Сила тяжести Двигатели для радиоуправляемых автомоделей
Двигатели для радиоуправляемых автомоделей Движение по окружности
Движение по окружности Электродинамика Максвелла: границы и перспективы обобщений и модификаций
Электродинамика Максвелла: границы и перспективы обобщений и модификаций Индикаторы напряжения
Индикаторы напряжения Статика. Понятия и определения
Статика. Понятия и определения Презентация на тему Проектная творческая работа по физике: миф или реальность
Презентация на тему Проектная творческая работа по физике: миф или реальность  Конструктивные изменения, внесенные в устройства техники ОАО Гомсельмаш
Конструктивные изменения, внесенные в устройства техники ОАО Гомсельмаш Явление электромагнитной индукции
Явление электромагнитной индукции Анализ сложной линейной электрической цепи постоянного тока
Анализ сложной линейной электрической цепи постоянного тока Импульс
Импульс Электростатика
Электростатика Дробилка безрешетная
Дробилка безрешетная Лекция 11. Крутильные колебания стержня
Лекция 11. Крутильные колебания стержня Элементы таблицы Менделеева
Элементы таблицы Менделеева