Содержание
- 2. Свойства ДВПФ. Линейность Пусть дана линейная комбинация сигналов: где a и b - постоянные коэффициенты Тогда
- 3. Свойства ДВПФ. Временной сдвиг Пусть дан сигнал, задержанный на величину k0: Спектр такого сигнала равен: Амплитудный
- 4. Свойства ДВПФ. Спектр свёртки сигналов Пусть дан сигнал, который сворачивает две последовательности: Спектр свёртки равен произведению
- 5. Свойства ДВПФ. Спектр произведения сигналов Пусть дан сигнал: Спектр произведения равен свёртке спектров:
- 6. Свойства ДВПФ. Теорема Парсеваля Пусть дан сигнал: Тогда для него будет справедливо такое утверждение: сумма квадрата
- 7. Свойства ДВПФ. Итоги Данные свойства позволяют вычислять спектры различных сигналов, не используя прямую формулу для вычисления
- 9. Скачать презентацию






 Строительство и эксплуатация зданий и сооружений. Связи и их реакции
Строительство и эксплуатация зданий и сооружений. Связи и их реакции Акустооптические модуляторы света
Акустооптические модуляторы света Примесные полупроводники
Примесные полупроводники Закон сохранения импульса
Закон сохранения импульса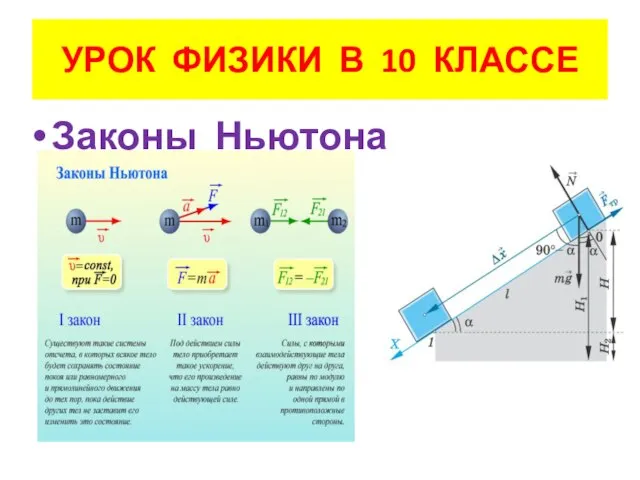 Презентация на тему Законы Ньютона (10 класс)
Презентация на тему Законы Ньютона (10 класс)  Сопротивление материалов
Сопротивление материалов Простые механизмы
Простые механизмы Применение аккумуляторов
Применение аккумуляторов Закон сохранения импульса
Закон сохранения импульса Электрическая цепь. Электрическая схема. Условные обозначения
Электрическая цепь. Электрическая схема. Условные обозначения Радиоактивные превращения атомных ядер
Радиоактивные превращения атомных ядер Презентация на тему Электризация тел. Два рода зарядов (8 класс)
Презентация на тему Электризация тел. Два рода зарядов (8 класс)  Антенно-мачтовые сооружения
Антенно-мачтовые сооружения Скорость. Расчет пути и времени движения
Скорость. Расчет пути и времени движения Физическая лихорадка. Методические указания
Физическая лихорадка. Методические указания 11, задание и конспект по электростатике
11, задание и конспект по электростатике Презентация на тему Физические величины измерение физических величин
Презентация на тему Физические величины измерение физических величин  Установка механической блокировки
Установка механической блокировки Токи и напряжения в длинных линиях электропередач
Токи и напряжения в длинных линиях электропередач Презентация на тему Электромагнит
Презентация на тему Электромагнит  Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения Электромагнитная индукция. Закон электромагнитной индукции. Индуктивность. Энергия магнитного поля катушки с током
Электромагнитная индукция. Закон электромагнитной индукции. Индуктивность. Энергия магнитного поля катушки с током Презентация на тему Механическая работа и мощность (10 класс)
Презентация на тему Механическая работа и мощность (10 класс)  Автоматическое управление. Типовая упрощенная структура САУ
Автоматическое управление. Типовая упрощенная структура САУ Кинематика. 10 класс
Кинематика. 10 класс Светодиодная лампа. Открытый городской конкурс научно-технических проектов школьников Инженерный старт – 2019
Светодиодная лампа. Открытый городской конкурс научно-технических проектов школьников Инженерный старт – 2019 Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения Машина - техническое приспособление, выполняющее механические движения для преобразования энергии
Машина - техническое приспособление, выполняющее механические движения для преобразования энергии