Основы молекулярно-кинетической теории

Макроскопические тела- тела состоящие из большого числа молекул
Статистический метод – основан на том, что св-ва макроскопической сис-мы опр-ся св-ми частиц сис-мы и усредненными значениями хар-к этих частиц ( скорость, энергия и пр.)
Термодинамический метод – основан на том, что макроскопические тела могут обмениваться энергией как с друг другом так и с внешней средой ( давление, объем, температура)

Молекулярно-кинетическая теория
Вещество состоит из мельчайших частиц (атомов или молекул)
Частицы в-ва находятся в непрерывном хаотическом движении, скорость которого определяет T тела
Между частицами существуют силы притяжения и оттталкивания

Fпр
Fот
F
Засисимость силы взаимодействия от расстояния
r > r0 – силы притяжения
r < r0 – силы отталкивания
r = r0 силы =0

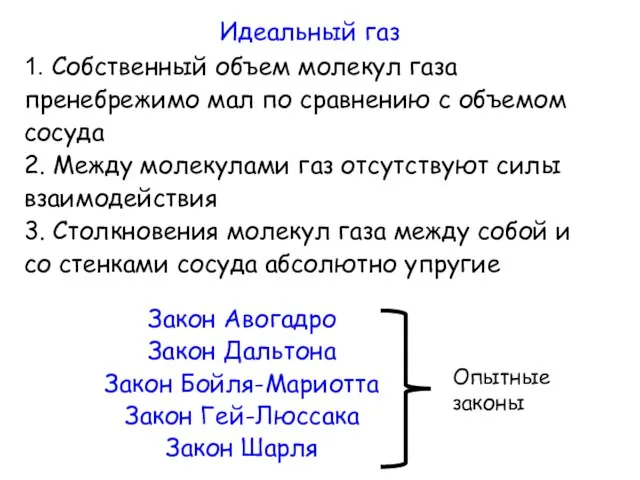
Идеальный газ
1. Собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда
2. Между молекулами газ отсутствуют силы взаимодействия
3. Столкновения молекул газа между собой и со стенками сосуда абсолютно упругие
Закон Авогадро
Закон Дальтона
Закон Бойля-Мариотта
Закон Гей-Люссака
Закон Шарля
Опытные законы

Закон Авогадро – моли любых газов при одинаковых T и P занимают одинаковый объем
При нормальных условиях Vm=22,41•10-3 м3
Постоянная Авогадро – число молекул в одном моле в-ва NA = 6,022•1023
Моль в-ва – кол-во в-ва, содержащее NA структурных элементов (атомов)
Закон Дальтона - давление смеси ид. газов, равно сумме парциальных давлений входящих в нее газов
P = P1 + P2 + P3 +…
Парциальное дав-ние – дав-ние, которое производил бы газ, если бы один занимал весь объем смеси при той же температуре

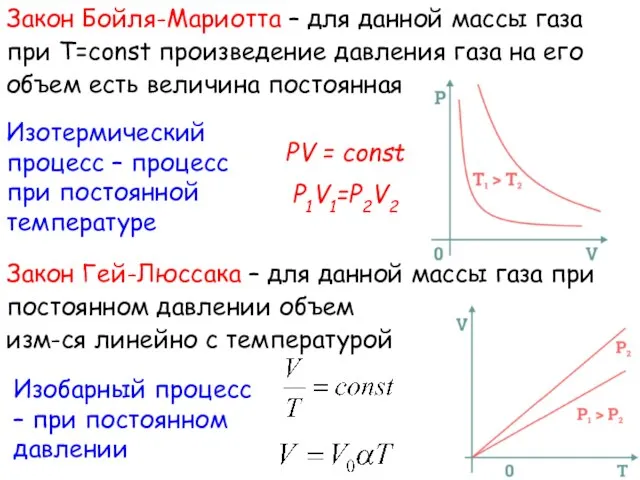
Закон Бойля-Мариотта – для данной массы газа при Т=const произведение давления газа на его объем есть величина постоянная
Изотермический процесс – процесс при постоянной температуре
PV = const
P1V1=P2V2
Закон Гей-Люссака – для данной массы газа при постоянном давлении объем
изм-ся линейно с температурой
Изобарный процесс – при постоянном давлении

Закон Шарля – давление данной массы при постоянном давлении изм-ся линейно с Т.
Процесс изохорный – при постоянном объеме
Из законов
b = const, ~ массе
Уравнение состояния идеального газа ( ур-ние Клайперона) связывает между собой термодинамические (макроскопические) параметры системы
b =???

При нормальных условиях
Газовая постоянная
M – Vm
m - V
Для произвольного объема V массой m
Из пропорции
ν -число молей газа
Уравнение Менделеева-Клайперона

Постоянная Больцмана
k = 1.38•10-23 Дж/К
Концентрация – число молекул в единице объема
Уравнение Менделеева-Клайперона
Давление идеального газа при данной t° прямо ~ концентрации его молекул
При одинаковых P и t° все газы содержат в единице объема одинаковое число молекул

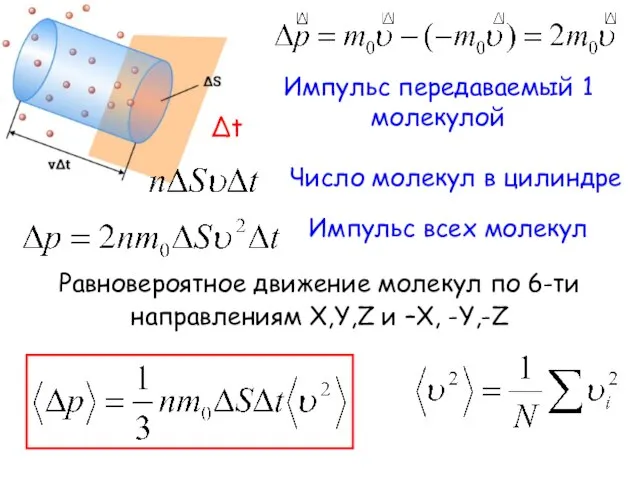
Импульс передаваемый 1 молекулой
Δt
Число молекул в цилиндре
Импульс всех молекул
Равновероятное движение молекул по 6-ти направлениям Х,Y,Z и –X, -Y,-Z

Сила давления на стенку сосуда
Делим на площадь
Основное уравнение МКТ
Среднее зн-ние кинет. энергии поступ. дв-ния молекул
Давление идеального газа опр-ся средним зн-нием кинет. энергии молекул
Температура явл-ся мерой средней энергии молекул

Для данного газа средняя квад-ная скорость зависит только от температуры
Статистическая хар-ка!!!!!
Δυ → В каждом интервале будет нах-ся ΔN молекул с этой скоростью – распределение числа молекул по скоростям

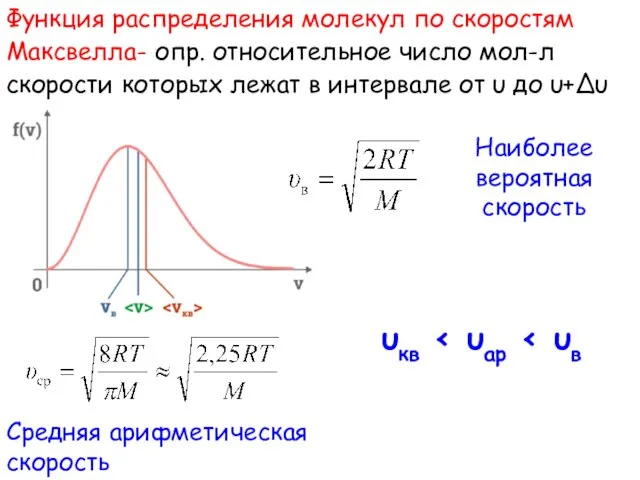
Функция распределения молекул по скоростям Максвелла- опр. относительное число мол-л скорости которых лежат в интервале от υ до υ+Δυ
Наиболее вероятная скорость
Средняя арифметическая скорость
υкв < υар < υв

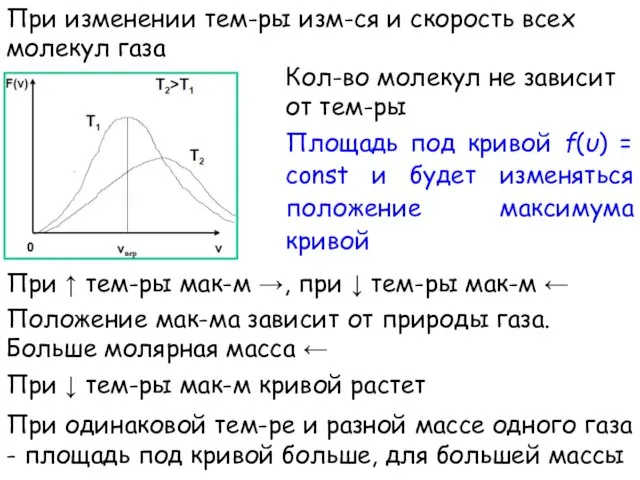
При изменении тем-ры изм-ся и скорость всех молекул газа
Площадь под кривой f(υ) = const и будет изменяться положение максимума кривой
Кол-во молекул не зависит от тем-ры
При ↑ тем-ры мак-м →, при ↓ тем-ры мак-м ←
Положение мак-ма зависит от природы газа. Больше молярная масса ←
При ↓ тем-ры мак-м кривой растет
При одинаковой тем-ре и разной массе одного газа - площадь под кривой больше, для большей массы

P убывает с высотой тем быстрее, чем тяжелее газ
Обозначим P1 = P0 и h1=h0 , где P0 и h0 давление и высота на уровне моря
барометрическая формула

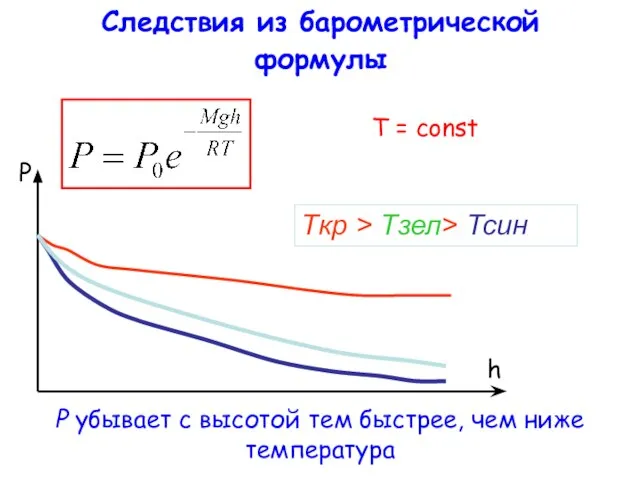
Следствия из барометрической формулы
Tкр > Tзел> Тсин
T = const
P убывает с высотой тем быстрее, чем ниже температура