Содержание
- 2. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. ЛЕКЦИИ. ВВЕДЕНИЕ Современная техника ставит перед инженерами множество задач, решение которых связано с исследованием
- 3. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. ЛЕКЦИИ. ВВЕДЕНИЕ Современная техника ставит перед инженерами множество задач, решение которых связано с исследованием
- 4. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. ЛЕКЦИИ. ВВЕДЕНИЕ Современная техника ставит перед инженерами множество задач, решение которых связано с исследованием
- 5. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. ЛЕКЦИИ. ВВЕДЕНИЕ Общим названием «механика» объединен целый комплекс дисциплин, занимающих различными вопросами механических взаимодействий
- 6. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. ЛЕКЦИИ. ВВЕДЕНИЕ Общим названием «механика» объединен целый комплекс дисциплин, занимающих различными вопросами механических взаимодействий
- 7. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. ЛЕКЦИИ. ВВЕДЕНИЕ Общим названием «механика» объединен целый комплекс дисциплин, занимающих различными вопросами механических взаимодействий
- 8. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. ЛЕКЦИИ. ВВЕДЕНИЕ Общим названием «механика» объединен целый комплекс дисциплин, занимающих различными вопросами механических взаимодействий
- 9. ОБЪЕКТЫ И МЕТОДЫ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ Материальной точкой называется геометрическая точка, обладающая массой - (МТ).
- 10. ОБЪЕКТЫ И МЕТОДЫ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ Материальной точкой называется геометрическая точка, обладающая массой - (МТ). Абсолютно твердым
- 11. ОБЪЕКТЫ И МЕТОДЫ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ Материальной точкой называется геометрическая точка, обладающая массой - (МТ). Абсолютно твердым
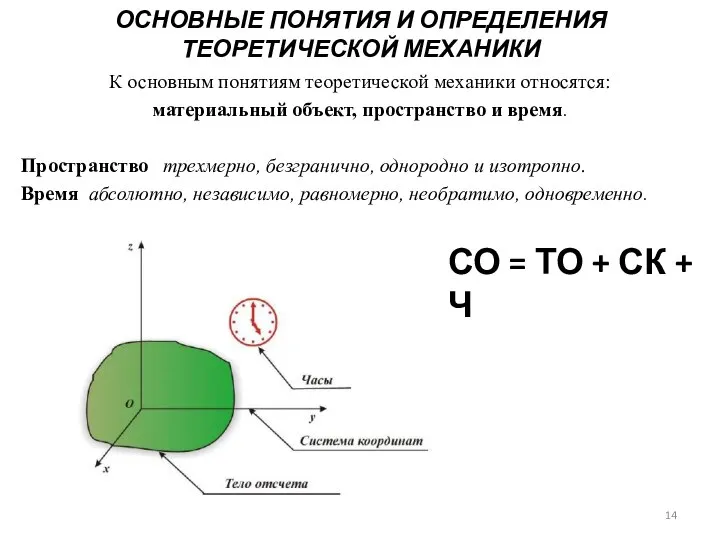
- 12. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ К основным понятиям теоретической механики относятся: материальный объект, пространство и
- 13. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ К основным понятиям теоретической механики относятся: материальный объект, пространство и
- 14. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ К основным понятиям теоретической механики относятся: материальный объект, пространство и
- 15. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ После того, как мы ввели понятие системы отсчета, мы можем
- 16. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ Материальные объекты, движение и равновесие которых приходится изучать, разделяются на
- 17. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ Материальные объекты, движение и равновесие которых приходится изучать, разделяются на
- 18. РОЛЬ И ЗНАЧЕНИЕ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ Теоретическую механику, в основу которой положены законы Галилея - Ньютона, часто
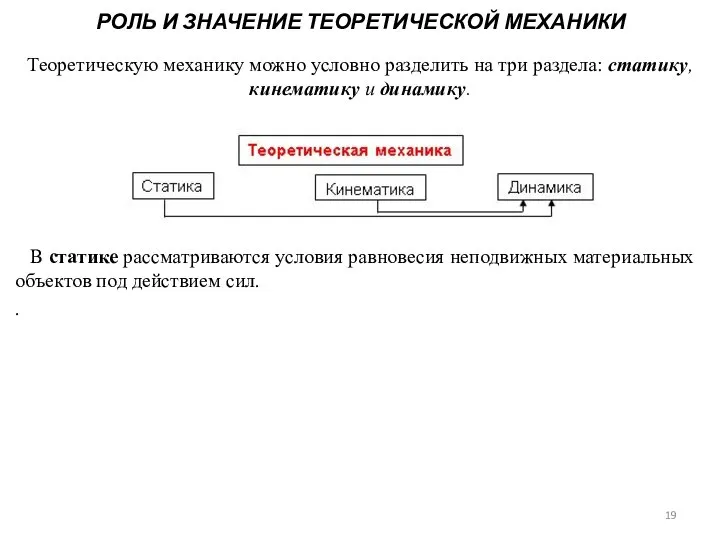
- 19. РОЛЬ И ЗНАЧЕНИЕ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ Теоретическую механику можно условно разделить на три раздела: статику, кинематику и
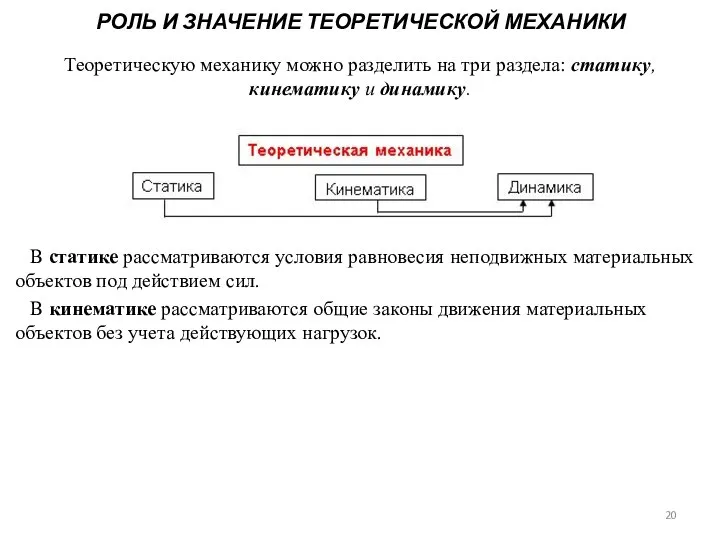
- 20. РОЛЬ И ЗНАЧЕНИЕ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ Теоретическую механику можно разделить на три раздела: статику, кинематику и динамику.
- 21. РОЛЬ И ЗНАЧЕНИЕ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ Теоретическую механику можно разделить на три раздела: статику, кинематику и динамику.
- 22. СТАТИКА ТВЕРДОГО ТЕЛА (ТТ) Статика есть общее учение о силах. В статике изучаются законы равновесия абсолютно
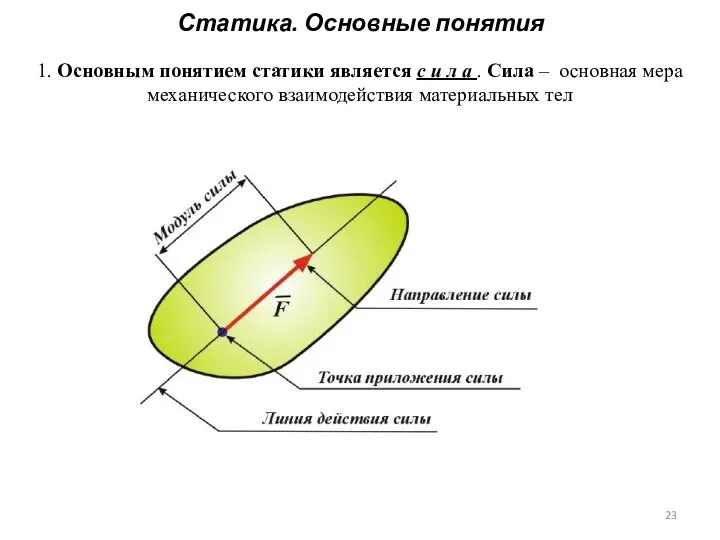
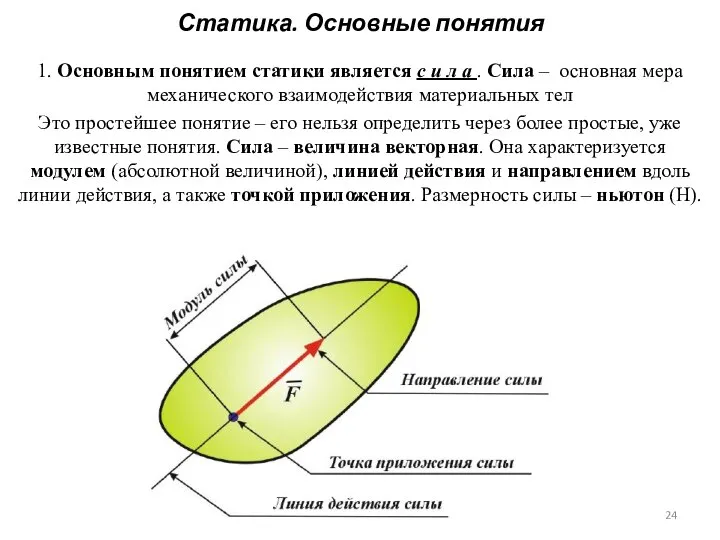
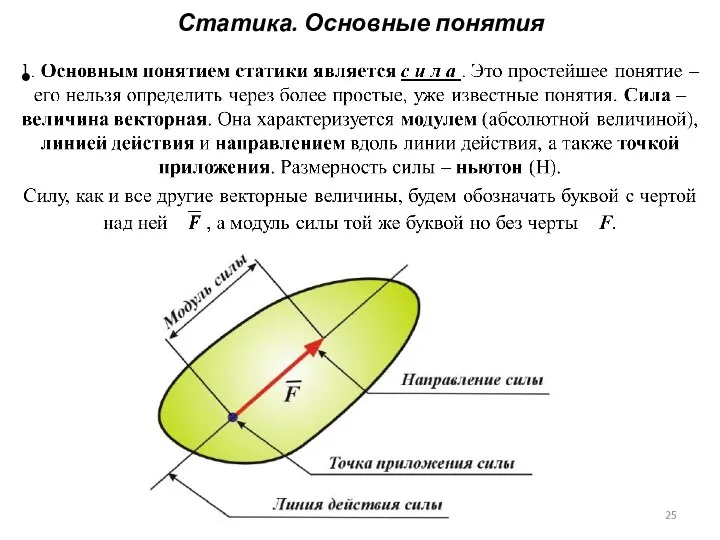
- 23. Статика. Основные понятия 1. Основным понятием статики является с и л а . Сила – основная
- 24. Статика. Основные понятия 1. Основным понятием статики является с и л а . Сила – основная
- 25. Статика. Основные понятия
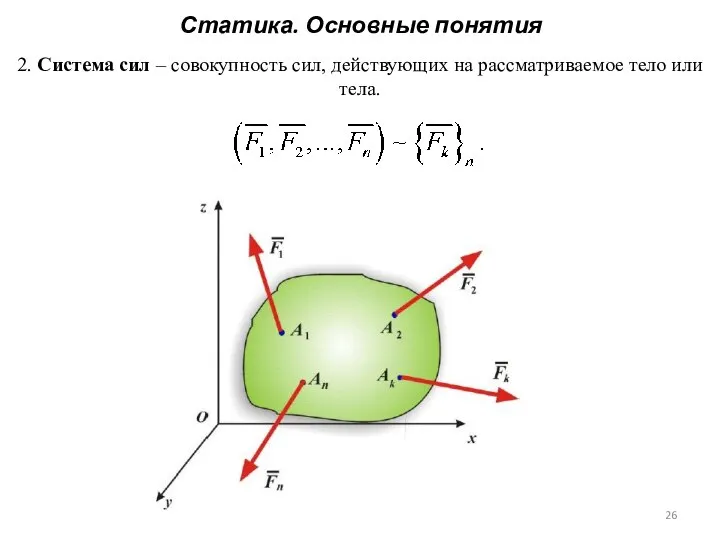
- 26. Статика. Основные понятия 2. Система сил – совокупность сил, действующих на рассматриваемое тело или тела.
- 27. Статика. Основные понятия Система сил может быть: сходящейся , если линии всех сил системы пересекаются в
- 28. Статика. Основные понятия Система сил может быть: сходящейся , если линии всех сил системы пересекаются в
- 29. Статика. Основные понятия Система сил может быть: сходящейся , если линии всех сил системы пересекаются в
- 30. Статика. Основные понятия 3. Если одну систему сил ,действующих на свободное твердое тело, можно заменить другой
- 31. Статика. Основные понятия 3. Если одну систему сил ,действующих на свободное твердое тело, можно заменить другой
- 32. Статика. Основные понятия 3. Если одну систему сил ,действующих на свободное твердое тело, можно заменить другой
- 33. Статика. Основные понятия 5. Сила называется уравновешивающей данную систему сил, если она вместе с этой системой
- 34. Статика. Основные понятия 5. Сила называется уравновешивающей данную систему сил, если она вместе с этой системой
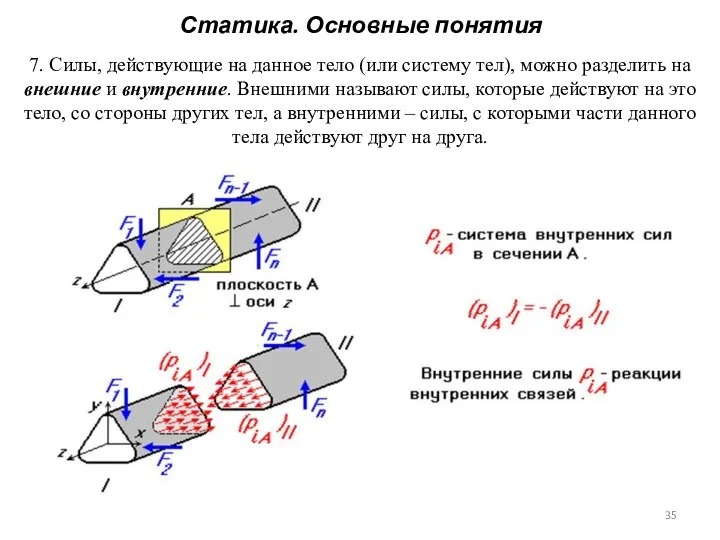
- 35. Статика. Основные понятия 7. Силы, действующие на данное тело (или систему тел), можно разделить на внешние
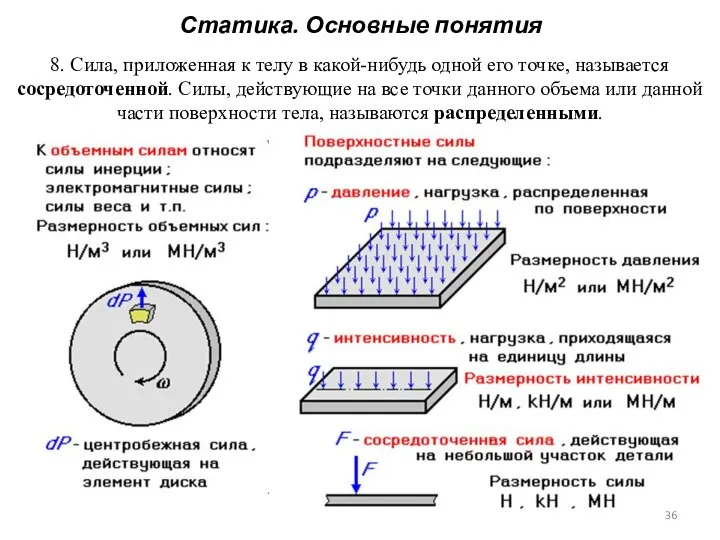
- 36. Статика. Основные понятия 8. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Силы,
- 37. Статика. Основные понятия Задачами статики являются: Преобразование систем сил, действующих на твердое тело, в системы их
- 38. Статика. Основные понятия Задачами статики являются: Преобразование систем сил, действующих на твердое тело, в системы их
- 39. Статика. Основные понятия Задачами статики являются: Преобразование систем сил, действующих на твердое тело, в системы их
- 40. Статика. Аксиомы статики Аксиома №1: если на свободное абсолютно твердое тело действуют две силы, то тело
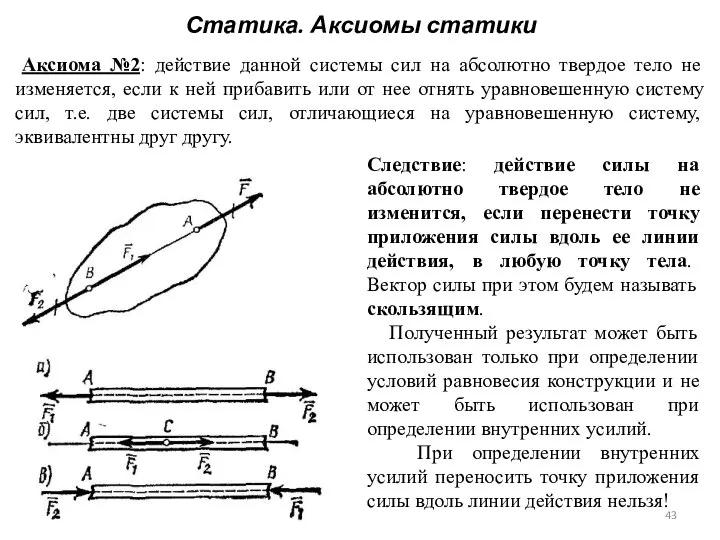
- 41. Статика. Аксиомы статики Аксиома №2: действие данной системы сил на абсолютно твердое тело не изменяется, если
- 42. Статика. Аксиомы статики Аксиома №2: действие данной системы сил на абсолютно твердое тело не изменяется, если
- 43. Статика. Аксиомы статики Аксиома №2: действие данной системы сил на абсолютно твердое тело не изменяется, если
- 44. Статика. Аксиомы статики Аксиома №3: Закон параллелограмма сил: две силы, приложенные к телу в одной точке,
- 45. Статика. Аксиомы статики Аксиома №3: Закон параллелограмма сил: две силы, приложенные к телу в одной точке,
- 46. Статика. Аксиомы статики Аксиома №4: закон равенства действия и противодействия: при всяком действии одного материального тела
- 47. Статика. Аксиомы статики Аксиома №4: закон равенства действия и противодействия: при всяком действии одного материального тела
- 48. Статика. Аксиомы статики Аксиома №5: принцип отвердевания: равновесие изменяемого (деформируемого тела), находящегося под действием данной системы
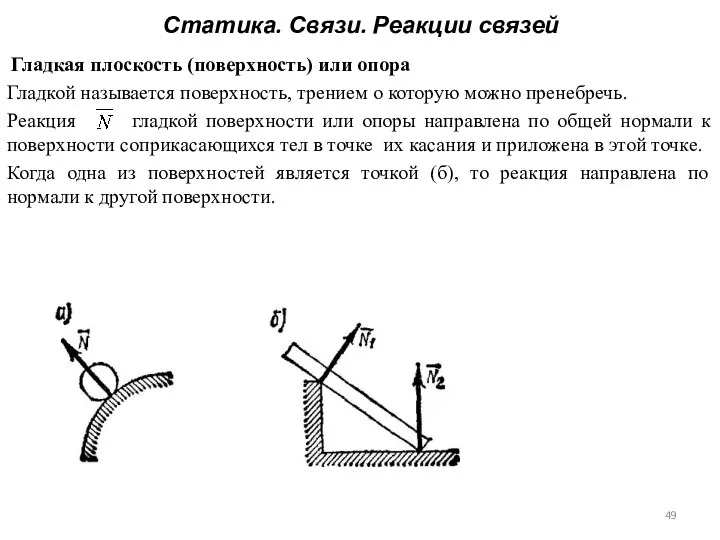
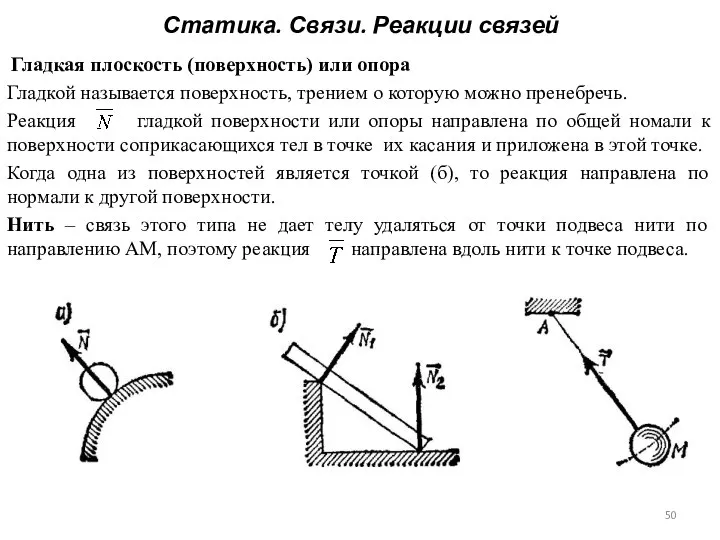
- 49. Статика. Связи. Реакции связей Гладкая плоскость (поверхность) или опора Гладкой называется поверхность, трением о которую можно
- 50. Статика. Связи. Реакции связей Гладкая плоскость (поверхность) или опора Гладкой называется поверхность, трением о которую можно
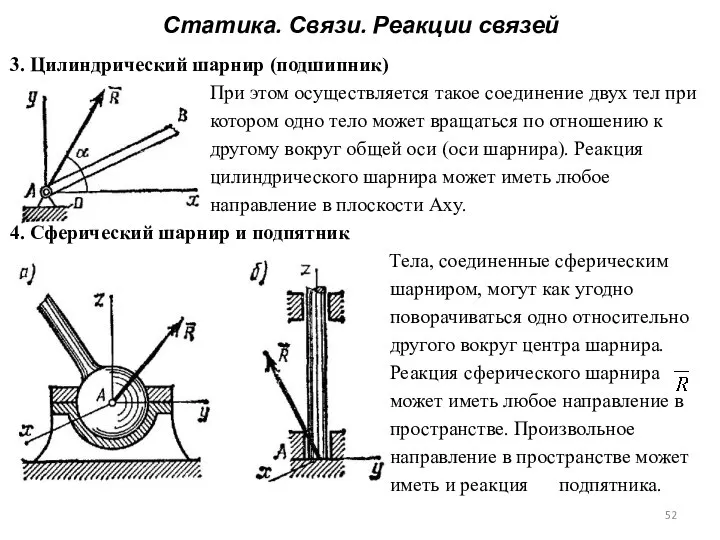
- 51. Статика. Связи. Реакции связей 3. Цилиндрический шарнир (подшипник) При этом осуществляется такое соединение двух тел при
- 52. Статика. Связи. Реакции связей 3. Цилиндрический шарнир (подшипник) При этом осуществляется такое соединение двух тел при
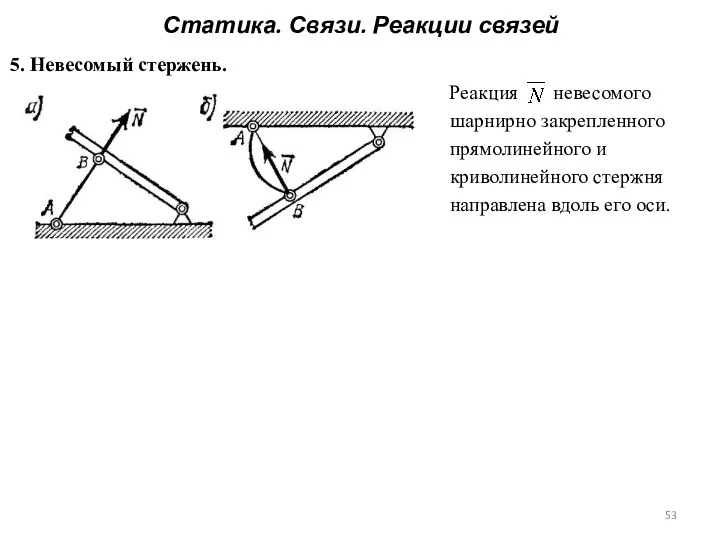
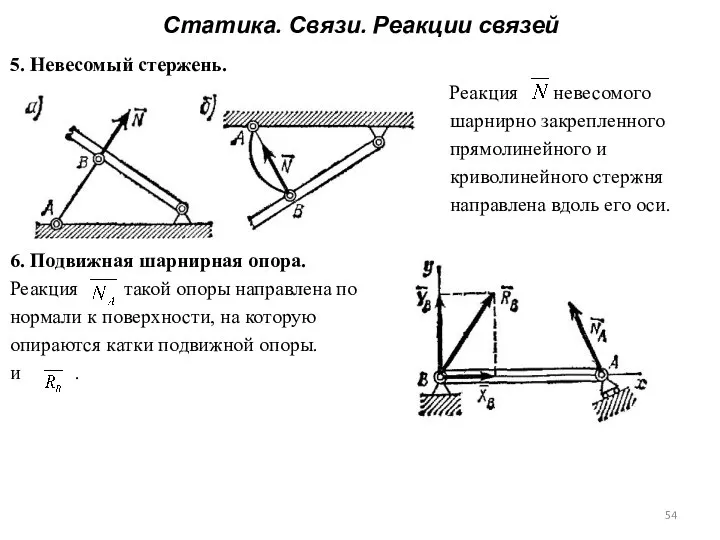
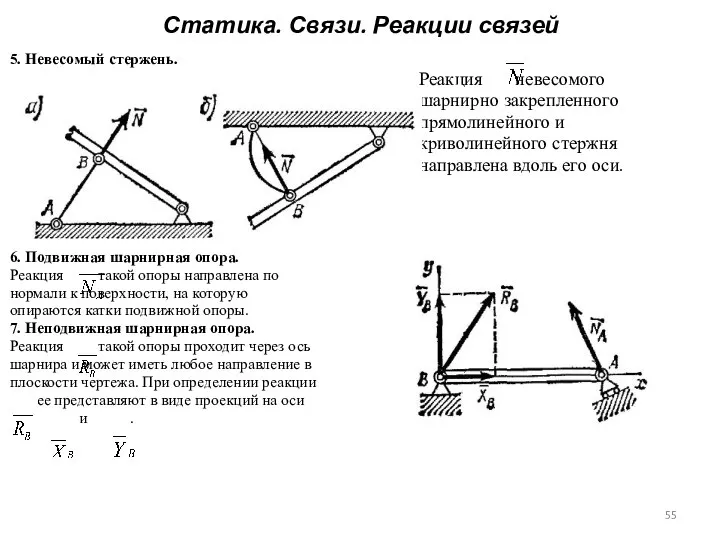
- 53. Статика. Связи. Реакции связей 5. Невесомый стержень. Реакция невесомого шарнирно закрепленного прямолинейного и криволинейного стержня направлена
- 54. Статика. Связи. Реакции связей 5. Невесомый стержень. Реакция невесомого шарнирно закрепленного прямолинейного и криволинейного стержня направлена
- 55. Статика. Связи. Реакции связей 5. Невесомый стержень. Реакция невесомого шарнирно закрепленного прямолинейного и криволинейного стержня направлена
- 56. Статика. Связи. Реакции связей 8. Скользящая заделка. Реакции такой опоры представлены сосредоточенной силой ( ), и
- 58. Скачать презентацию







































 Решение задач на силу Ампера и силу Лоренца. Урок 51
Решение задач на силу Ампера и силу Лоренца. Урок 51 Механические колебания
Механические колебания Плотность вещества
Плотность вещества Прямолинейное равномерное движение
Прямолинейное равномерное движение Микроподводные движители. Виды микро-движителей
Микроподводные движители. Виды микро-движителей Лазерные фазовые дальномеры
Лазерные фазовые дальномеры Презентация на тему Конденсаторы (10 класс)
Презентация на тему Конденсаторы (10 класс)  Стенд для лабораторных работ Зубчатые передачи
Стенд для лабораторных работ Зубчатые передачи Давление твёрдых тел, жидкостей и газов
Давление твёрдых тел, жидкостей и газов Антенна. Классификация радиопередающих устройств
Антенна. Классификация радиопередающих устройств Процедура работы с браком
Процедура работы с браком Магнитное поле
Магнитное поле Автомобили. 3 класс
Автомобили. 3 класс Атом - сложная частица
Атом - сложная частица МФТИ 5 вариант. Подготовка к ЕГЭ
МФТИ 5 вариант. Подготовка к ЕГЭ Внешний фотоэффект. Изучение законов внешнего фотоэффекта
Внешний фотоэффект. Изучение законов внешнего фотоэффекта Презентация на тему Робототехника и Искусственный Интеллект
Презентация на тему Робототехника и Искусственный Интеллект  Сила упругости. Закон Гука. Вес тела
Сила упругости. Закон Гука. Вес тела Линзы. Виды линз. Условное обозначение линз. Собирающие линзы
Линзы. Виды линз. Условное обозначение линз. Собирающие линзы Свойства металлов и сплавов
Свойства металлов и сплавов Лабораторная работа Определение положения центра тяжести плоской фигуры
Лабораторная работа Определение положения центра тяжести плоской фигуры Введение в гидродинамику
Введение в гидродинамику Мир без денег – это возможно?
Мир без денег – это возможно? Закон Ома, расчёт сопротивления, виды соединения проводников. Подготовка к контрольной
Закон Ома, расчёт сопротивления, виды соединения проводников. Подготовка к контрольной Классификация композитов. Волокна и матрицы. Структура и назначение
Классификация композитов. Волокна и матрицы. Структура и назначение Полупроводники. Проводимость полупроводников
Полупроводники. Проводимость полупроводников Динамика поступательного движения
Динамика поступательного движения Основные потребители реактивной мощности на промышленных предприятиях. Основные принципы размещения компенсирующих устройств
Основные потребители реактивной мощности на промышленных предприятиях. Основные принципы размещения компенсирующих устройств