Слайд 2Условия обучения
По итогам изучения дисциплины проводится экзамен
В течение семестра необходимо выполнить все

задания по календарному плану, который опубликован на Учебном портале
Для допуска на сессию набрать 40 баллов
Слайд 3Список литературы
1. Бесекерский В.Л., Попов Е.П. Теория систем автоматического управления. СПб.: Профессия,

2003.
2. Теория автоматического управления. Ч. 1 Теория линейных систем автоматического управления / под ред. Академика А.А.Воронова. 2-е изд. М.: Высшая школа, 1984.
3. Босс В. Лекции по теории управления. Т.1: Автоматическое регулирование. М.: ЛЕНАНД, 2017
4. Рощин А.В. Основы теории автоматического управления. Учебное пособие. М.: МГУПИ, 2007
Слайд 4Темы дисциплины
Управление и информатика, построение модели простого объекта, общие принципы системной организации,

построение передаточной функции, формы представления моделей, инвариантность и чувствительность систем управления, уравнения в нормальной форме, задача Коши, передаточная матрица. Математические модели объектов и систем управления, переходные и частотные характеристики объекта, весовая функция, переходная функция, частотные характеристики, логарифмические частотные характеристики, асимптотические логарифмические частотные характеристики.
Слайд 5Темы дисциплины
Проблема устойчивости, типовые элементарные звенья, интегрирующее звено, апериодическое звено, колебательное звено,

дифференцирующее звено, соединение звеньев. Исследование системы автоматического управления. построение логарифмических частотных характеристик, проверка устойчивости системы, запас устойчивости по фаз, запас устойчивости по амплитуде.
Слайд 6Решение типовых задач теории управления. Устойчивость.

Слайд 7Необходимое условие устойчивости

Слайд 9Частный случай. Критерий Вышнеградского.
Критерий устойчивости для системы с характеристическим уравнением третьего порядка:
Проверить

соответствие критерия Вышнеградского критерию Гурвица.
Слайд 10Решение задач
Определить устойчивость замкнутой и разомкнутой системы по известной передаточной функции разомкнутой

системы
Характеристическое уравнение разомкнутой системы
Найдём передаточную функцию замкнутой системы
Характеристическое уравнение замкнутой системы
2•4 > 3•1 - т.е. система устойчива
Слайд 11Задачи для самостоятельного решения
1.
2.
3.
4.

Слайд 12Задачи для самостоятельного решения
Известна передаточная функция разомкнутой системы. Определить значение постоянной времени

T, при котором замкнутая система окажется на границе устойчивости.
1.
2.
Слайд 13Домашнее задание
Определить устойчивость замкнутой и разомкнутой системы по известной передаточной функции разомкнутой

системы
1.
2.
Известна передаточная функция разомкнутой системы. Определить значение постоянной времени T, при котором замкнутая система окажется на границе устойчивости.
1.
Слайд 14Примеры годографов Михайлова
Годограф Михайлова устойчивых систем имеет спиралевидную форму, начинается при
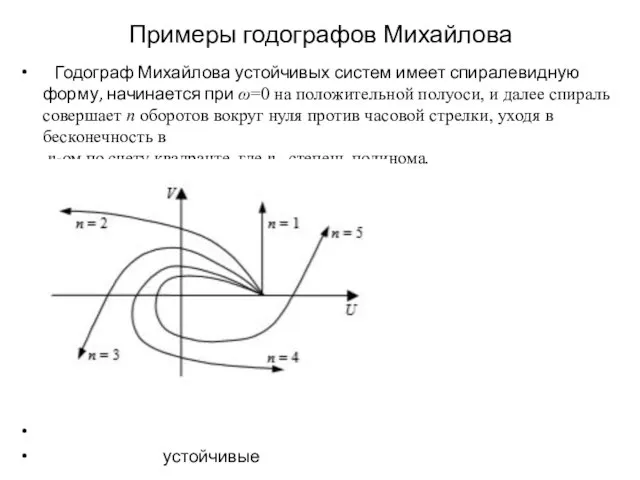
ω=0 на положительной полуоси, и далее спираль совершает n оборотов вокруг нуля против часовой стрелки, уходя в бесконечность в
n-ом по счету квадранте, где n –степень полинома.
устойчивые
Слайд 15Критерий Михайлова
Для того, чтобы САУ была устойчива необходимо и достаточно, чтобы годограф

Михайлова при изменении частоты от 0 до ∞ , начинаясь при ω=0
на вещественной положительной полуоси, обходил против часовой стрелки последовательно n квадрантов координатной плоскости .
Годограф Михайлова относится к знаменателю передаточной функции.
Пример. Оценить устойчивость АС по критерию Михайлова, если известен характеристический полином замкнутой системы
Слайд 16Критерий Михайлова
Для построения кривой Михайлова определим вещественную и мнимую части функции
Определим
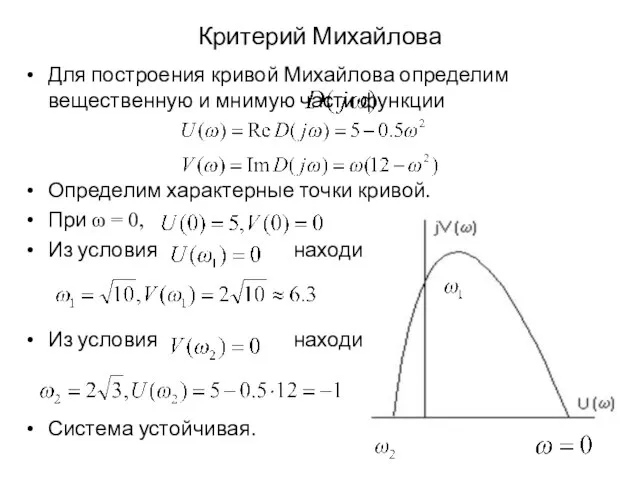
характерные точки кривой.
При ω = 0,
Из условия находим
Из условия находим
Система устойчивая.
Слайд 17Задачи для самостоятельного решения
1.
2.
Домашнее задание

Слайд 18Критерий Найквиста
Если разомкнутая система устойчива, то для устойчивости замкнутой системы годограф W(i

ω) вообще не должен охватывать точку (-1, 0i) при изменении частоты от 0 до ∞ и повороте вектора годографа W(i ω) по часовой стрелке.
а) - разомкнутая система
б) – вспомогательная функция H(iω)
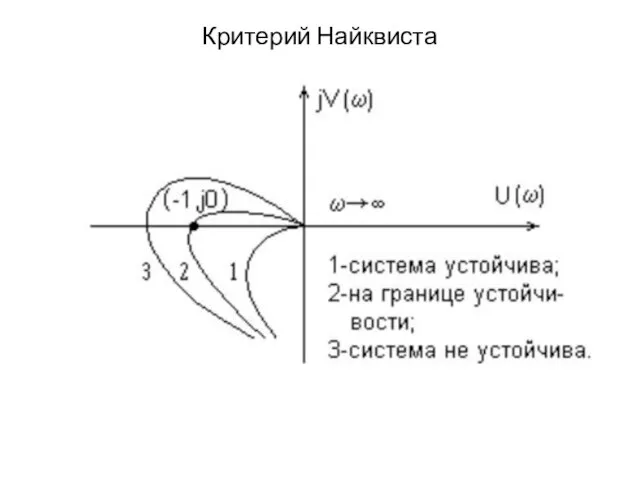
Слайд 20Критерий Найквиста
Следствие из критерия Найквиста
Если разомкнутая система неустойчива, то для устойчивости замкнутой
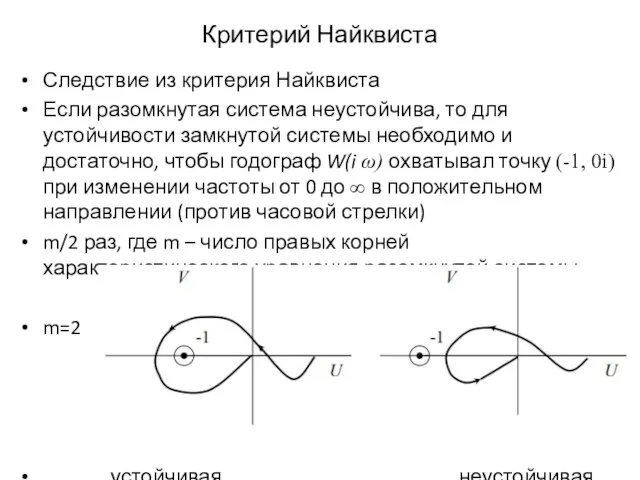
системы необходимо и достаточно, чтобы годограф W(i ω) охватывал точку (-1, 0i) при изменении частоты от 0 до ∞ в положительном направлении (против часовой стрелки)
m/2 раз, где m – число правых корней характеристического уравнения разомкнутой системы.
m=2
устойчивая неустойчивая
Слайд 21Критерий Найквиста
Разомкнутая система астатическая. (Знаменатель передаточной функции имеет нулевые корни). Годограф зеркально
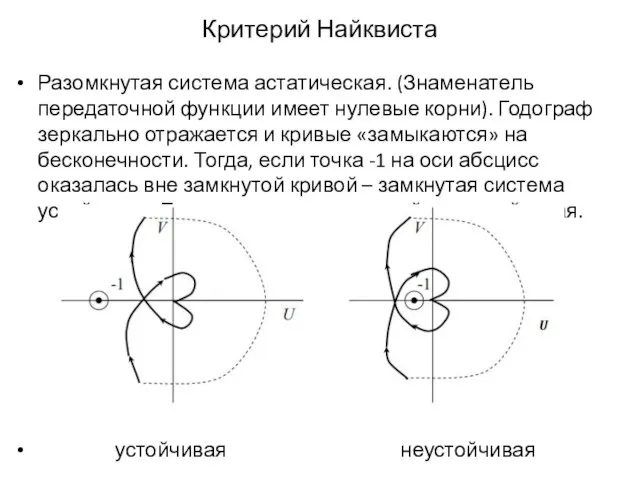
отражается и кривые «замыкаются» на бесконечности. Тогда, если точка -1 на оси абсцисс оказалась вне замкнутой кривой – замкнутая система устойчивая. Если охватывается кривой – неустойчивая.
устойчивая неустойчивая
Слайд 22Критерий Найквиста
Замкнутая система будет находиться на границе устойчивости, если годограф разомкнутой системы

проходит через точку -1 оси абсцисс. Аналитически это условие можно записать в виде
Пример. Дана передаточная функция разомкнутой системы:
Проверить с помощью критерия Найквиста, будет ли устойчива замкнутая система.
По критерию Гурвица разомкнутая система устойчива.
Найдём частотную характеристику.
Слайд 23Критерий Найквиста
Выделим действительную и мнимую части
По условию V(ω) = 0 находим частоты

пересечения годографом действительной оси и соответствующие значенияU(ω):
V(ω) = 0, , ,
U(0) = 2, U(2) =- 0.18
По условию U(ω) = 0, находим частоту пересечения годографом мнимой оси и соответствующее значение V (ω):
U(ω) = 0, ,
V (0.58)=-0.94
Слайд 24Критерий Найквиста
Для ω = 1 получаем U(1) = – 0.3, V(1) =
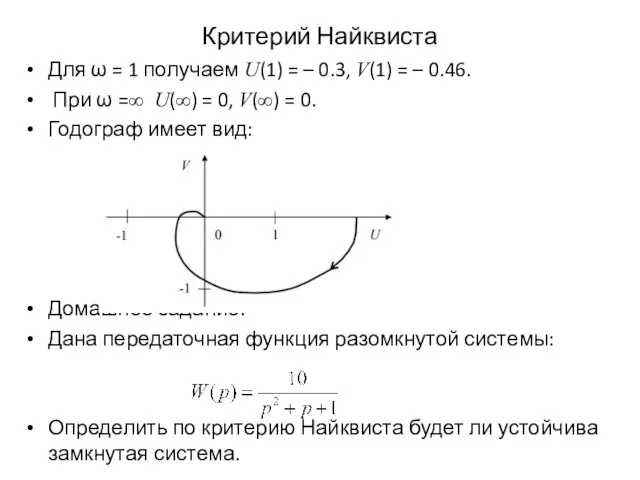
– 0.46.
При ω =∞ U(∞) = 0, V(∞) = 0.
Годограф имеет вид:
Домашнее задание.
Дана передаточная функция разомкнутой системы:
Определить по критерию Найквиста будет ли устойчива замкнутая система.






















 Гармонические колебания
Гармонические колебания Презентация на тему Электричество в доме (8 класс)
Презентация на тему Электричество в доме (8 класс)  Методы получения изображений видимого излучения
Методы получения изображений видимого излучения Законы Ньютона
Законы Ньютона Модели молекул простого и сложного вещества
Модели молекул простого и сложного вещества Энергия ядерных превращений. Схемы распада
Энергия ядерных превращений. Схемы распада Электрическое поле. Напряженность
Электрическое поле. Напряженность Механическое движение
Механическое движение Дифракция. Дифракция Френеля. Лекция 3
Дифракция. Дифракция Френеля. Лекция 3 Относительность движения. Инерциальные системы отсчета. Первый закон Ньютона
Относительность движения. Инерциальные системы отсчета. Первый закон Ньютона Механическое движение (7 класс)
Механическое движение (7 класс) Электрический ток в различных средах
Электрический ток в различных средах авторы: Маньков Данил И пономарёв глеб Электромагнитные явления
авторы: Маньков Данил И пономарёв глеб Электромагнитные явления Сборка регулировка и испытание КШМ и ГРМ двигателей
Сборка регулировка и испытание КШМ и ГРМ двигателей Модель копия самолёта И 5. Масштаб 1: 9. Стендовая модель
Модель копия самолёта И 5. Масштаб 1: 9. Стендовая модель Величайшие открытия физики
Величайшие открытия физики Cокол Тысячелетия 10,08
Cокол Тысячелетия 10,08 История создания швейной машины
История создания швейной машины Работа и мощность в цепях постоянного тока. Закон Джоуля-Ленца. КПД источника в цепи постоянного тока
Работа и мощность в цепях постоянного тока. Закон Джоуля-Ленца. КПД источника в цепи постоянного тока Атомное ядро
Атомное ядро Презентация на тему Инфразвук
Презентация на тему Инфразвук  Взаимодействие тел
Взаимодействие тел Инерция (7 класс)
Инерция (7 класс) Витая пара
Витая пара Плотность. Решение задач
Плотность. Решение задач Интерференция света
Интерференция света Закон всемирного тяготения. Прямолинейное и криволинейное движение
Закон всемирного тяготения. Прямолинейное и криволинейное движение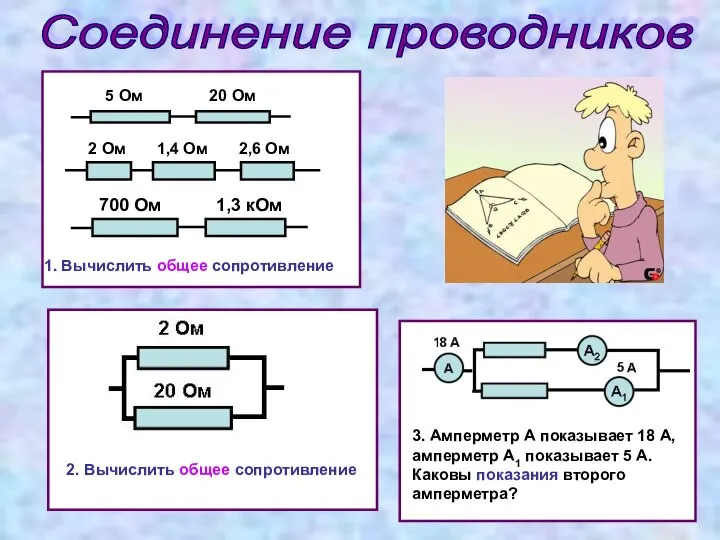 Соединение проводников
Соединение проводников