Содержание
- 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ МОДЕЛЬ ВРЕМЯ СООТНОШЕНИЕ
- 4. ХАРАКТЕРИСТИКИ И СХЕМА ВОЛН ЭЛЛИОТТА МОДЕЛЬ ИМПУЛЬС КОРРЕКЦИЯ
- 5. Движущие + Корректирующие = Цикл Самый высокий уровень 1 + 1 = 2 Уровнем ниже 5
- 6. ОБОЗНАЧЕНИЯ ВОЛН
- 7. Цикличность волн ВОЛНОВАЯ РАЗМЕТКА 1 2 3 4 5 А B C (5) (3) (1) (2)
- 9. БАЗОВАЯ ПЯТИВОЛНОВАЯ МОДЕЛЬ ИМПУЛЬСНЫЕ ВОЛНЫ КОРРЕКТИРУЮЩИЕ ВОЛНЫ
- 10. ИМПУЛЬСНЫЕ (ДВИЖУЩИЕ) ВОЛНЫ Волна 3 ВСЕГДА продвигается дальше окончания волны 1 1 2 3 5 волна
- 11. РАСТЯЖЕНИЕ ВОЛН РАСТЯЖЕНИЕ ПЕРВОЙ ВОЛНЫ 1 2 3 4 5
- 12. РАСТЯЖЕНИЕ ВОЛН РАСТЯЖЕНИЕ ТРЕТЬЕЙ ВОЛНЫ 1 2 3 4 5
- 13. РАСТЯЖЕНИЕ ВОЛН РАСТЯЖЕНИЕ ПЯТОЙ ВОЛНЫ 1 2 3 4 5
- 14. НЕУДАЧА (усечение волны) 1 2 3 5 4 неудача обычно происходит после чрезвычайно сильной третьей волны
- 15. 1 2 3 4 5 Диагональные (восходящие)треугольники треугольник является движущей моделью, хотя еще и не импульсом
- 16. (1) (2) (3) (4) (5) 1 2 3 4 5 Конечный треугольник Конечный треугольник является особым
- 17. Начальный треугольник 1 2 3 4 5 разновидность данной модели иногда появляется на месте волны 1
- 18. КОРРЕКТИРУЮЩИЕ ВОЛНЫ зигзаг, плоскость, треугольник двойная тройка, тройная двойка откаты никогда не являются «пятерками»
- 19. ЗИГЗАГИ Последовательность подволн – 5-3-5 А В С А В С одиночные
- 20. двойные зигзаги структуры аналогичны удлинению импульсной волны А В С А В С (А) (В) (С)
- 21. Плоскости последовательность подволн равна 3-3-5 А В С А В С
- 22. Треугольники содержат пять перекрывающих друг друга волн, которые подразделяются на модели 3-3-3-3-3 b a c d
- 23. когда треугольник формируется в четвертой волновой позиции, пятая волна иногда бывает стремительной b a c d
- 24. Двойные и тройные тройки А В С А В С (X) (W) (Y) А В С
- 25. Правила чередования простая модель Сложная модель – Простая модель Сложная модель
- 26. ФИБОНАЧЧИ Введение в мир Фибоначчи
- 27. ИСТОРИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ПРЕДПОСЫЛКИ ЗАКОНА ВОЛН Сколько пар кроликов, помещенных в загон, может быть произведено за
- 28. Последовательность Фибоначчи 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 Сумма любых
- 29. ГЕОМЕТРИЯ ФИБОНАЧЧИ Золотое сечение Любой отрезок может быть разделен таким образом, что соотношение между его меньшей
- 31. .618 .382 .382 ФИ И ФИНАНСОВЫЙ РЫНОК Модели финансового рынка являются повторяющимися 3 а b C
- 32. 1.00 1.00 1.00 1.618 1.00 0.618 Соотношения движущих и корректирующих волн 1 2 3 4 5
- 33. 0.618 1.00 1 2 3 4 5 1 2 3 4 5 0.382 0.382 1.00 0.618
- 34. Спасибо за участие в семинаре! Мы желаем Вам успехов!
- 35. фракталы Fractals Фрактал (. fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством САМОПОДОБИЯ (объект,
- 41. Двойная коррекция ПЯТОЙ ВОЛНЫ
- 42. Диагональные треугольники
- 45. Прехтер и его система разметки. Топография волновой карты Общие правила
- 46. 3 правила, считающиеся "нерушимыми"
- 47. Импульс
- 49. Скачать презентацию

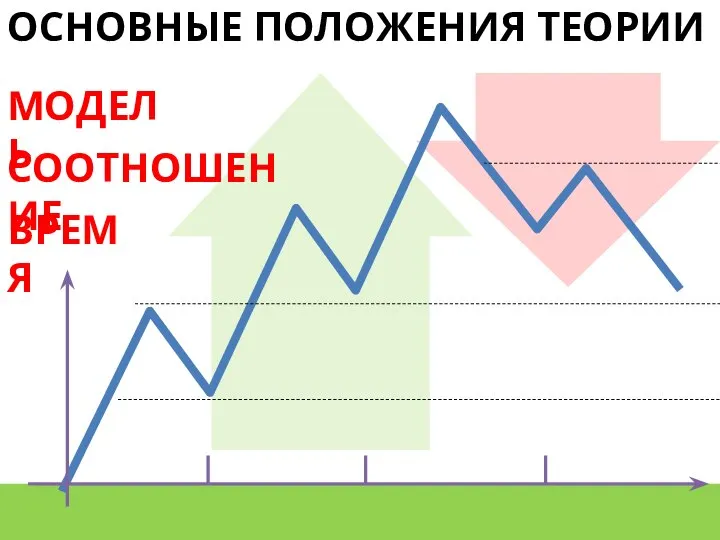
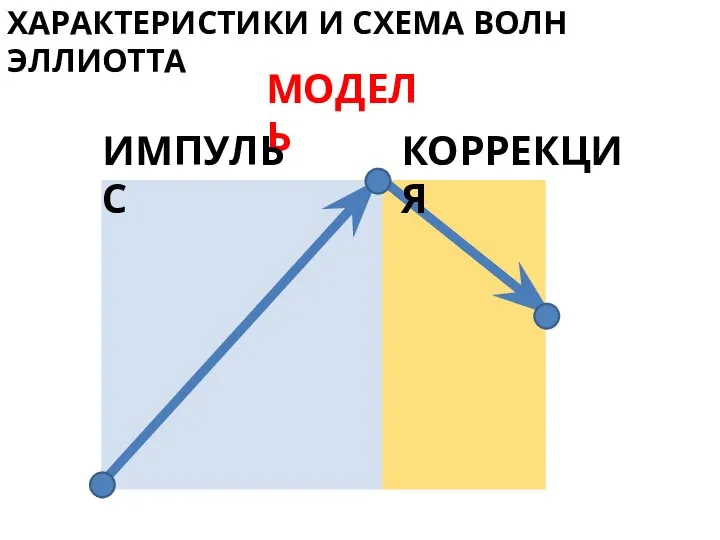
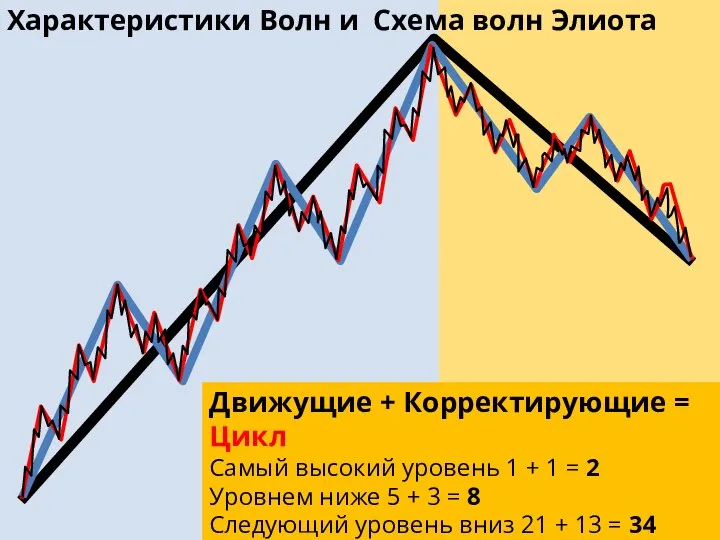
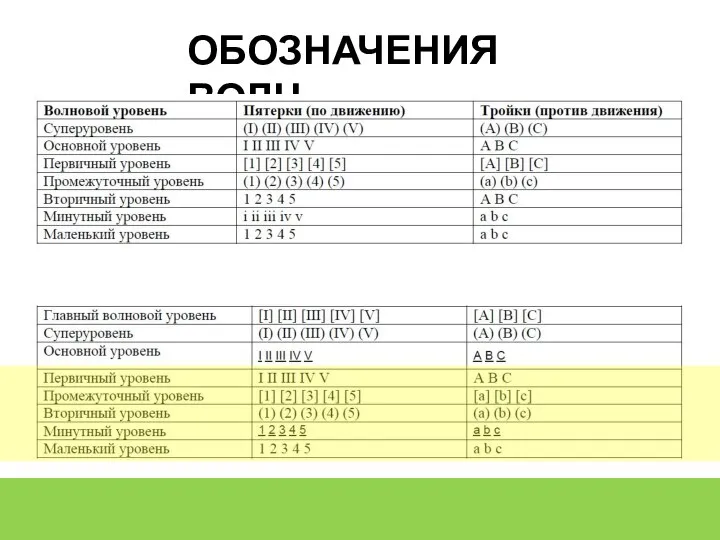
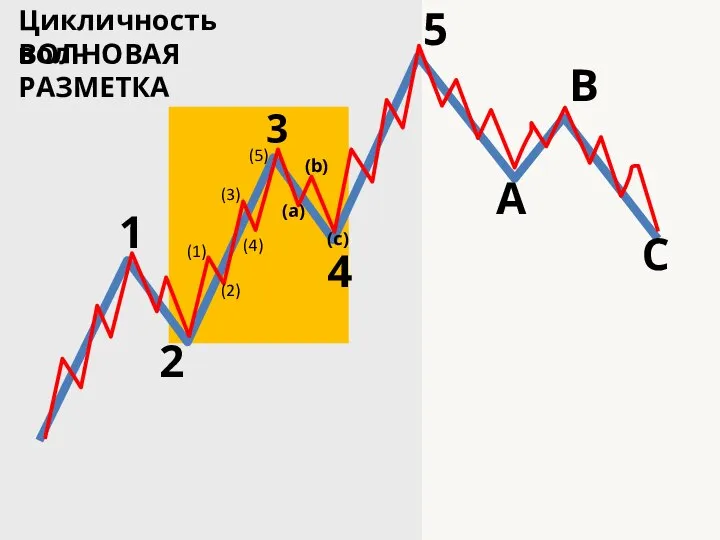
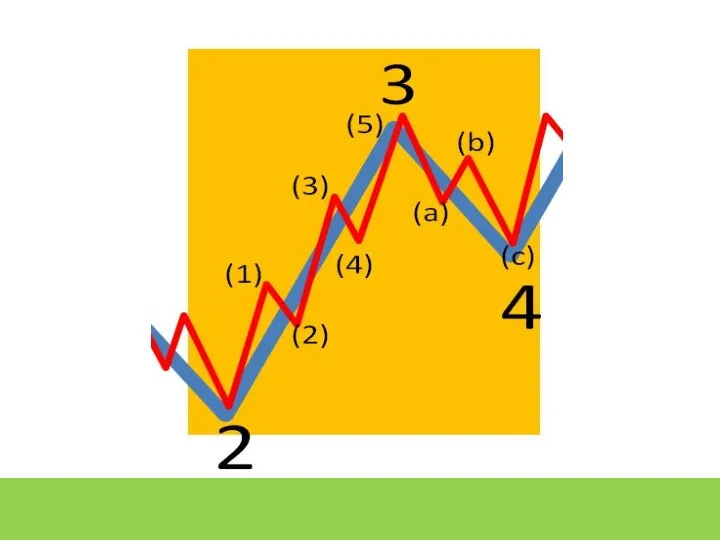
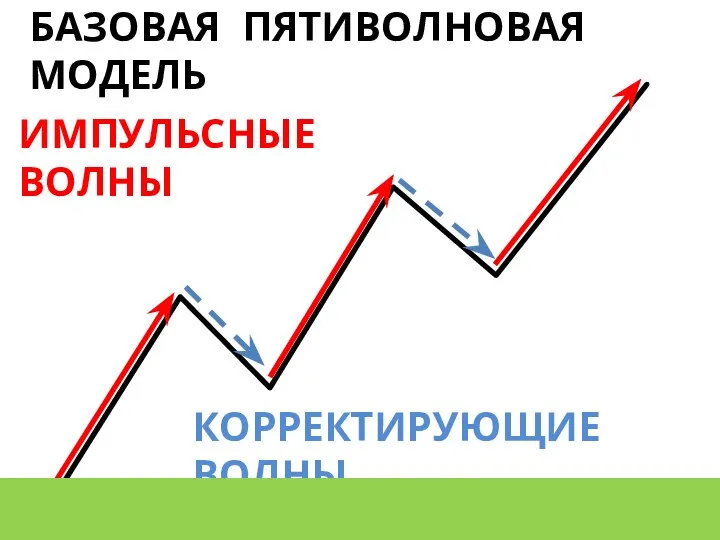
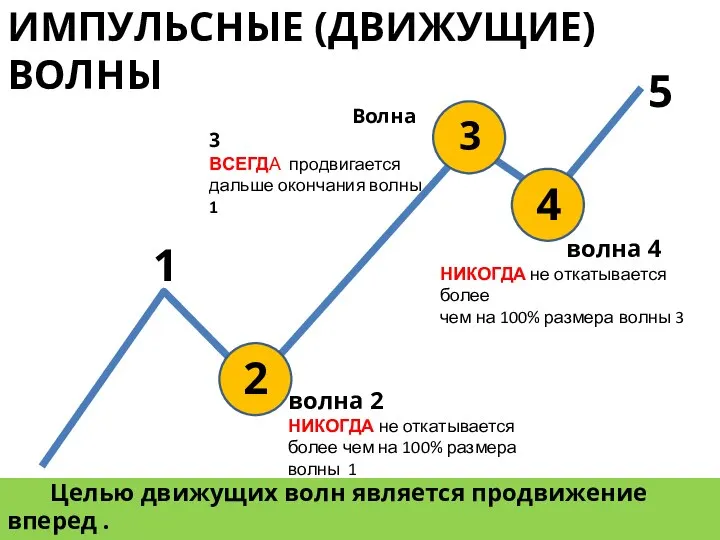
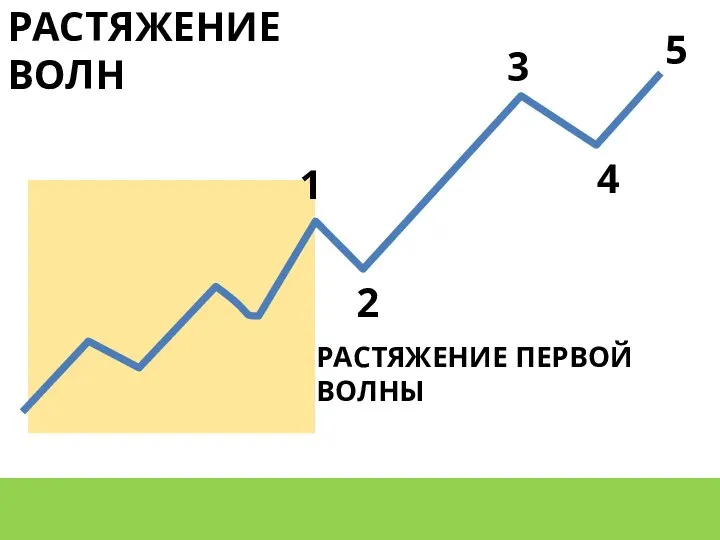
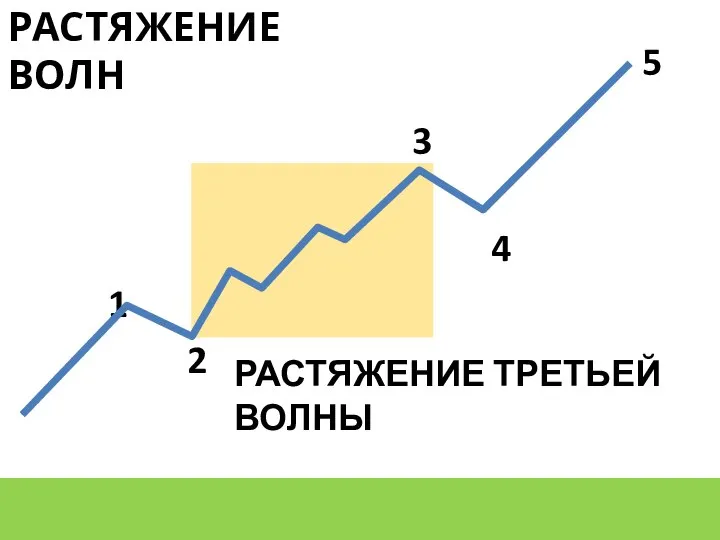
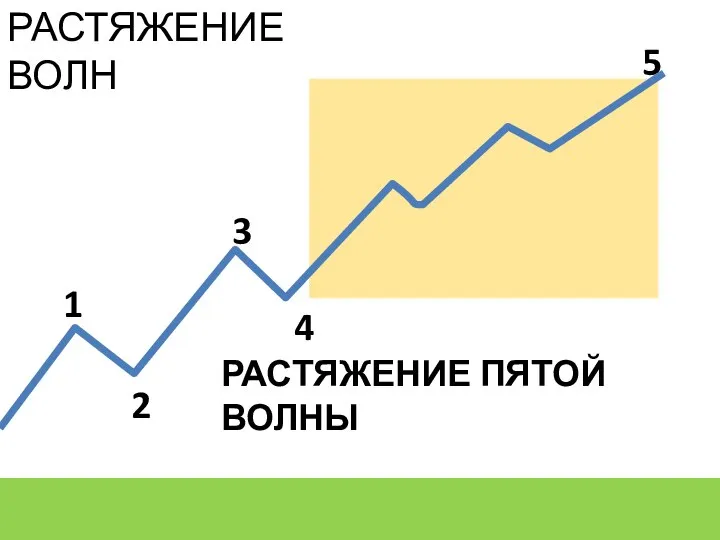
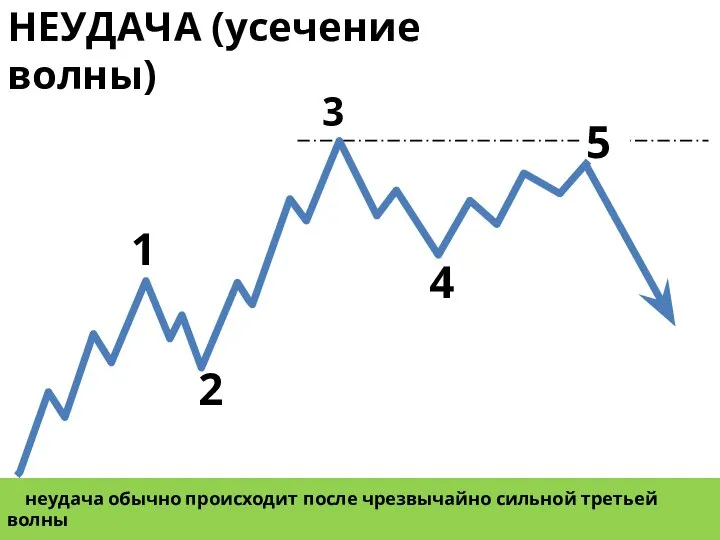
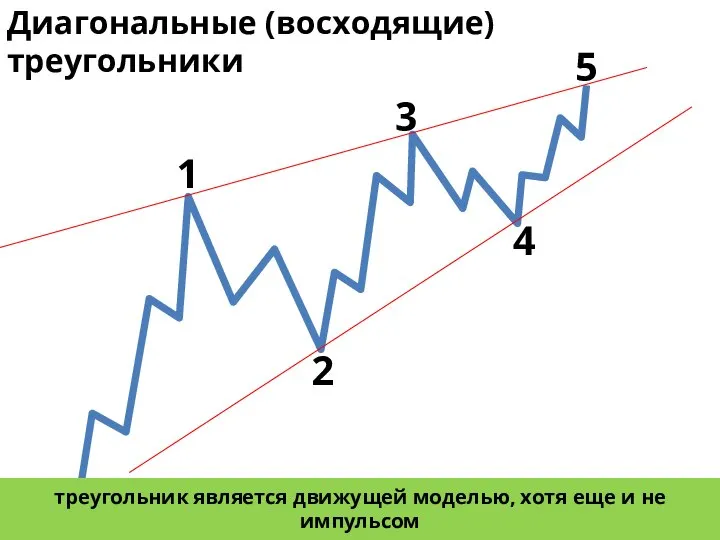
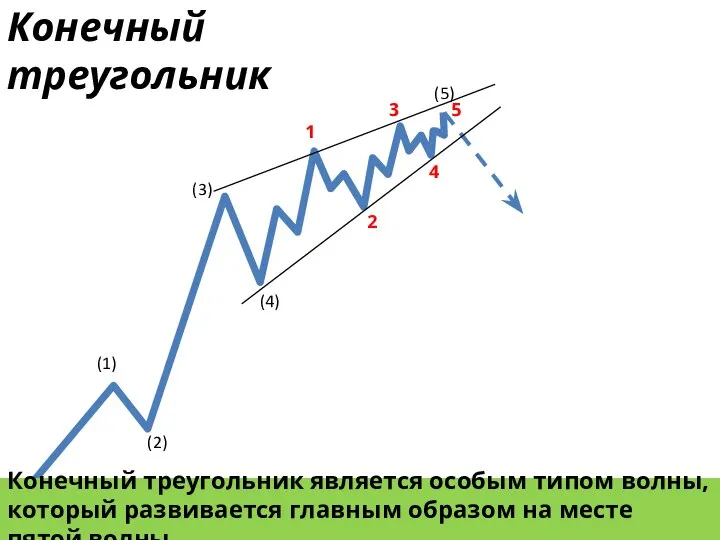
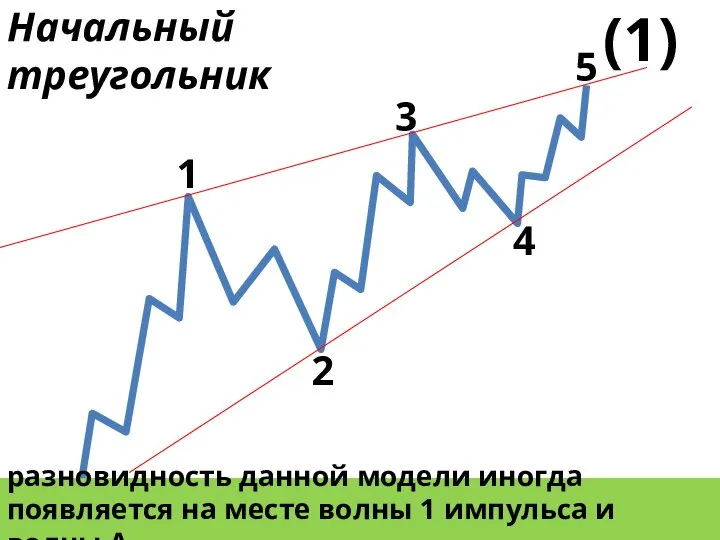

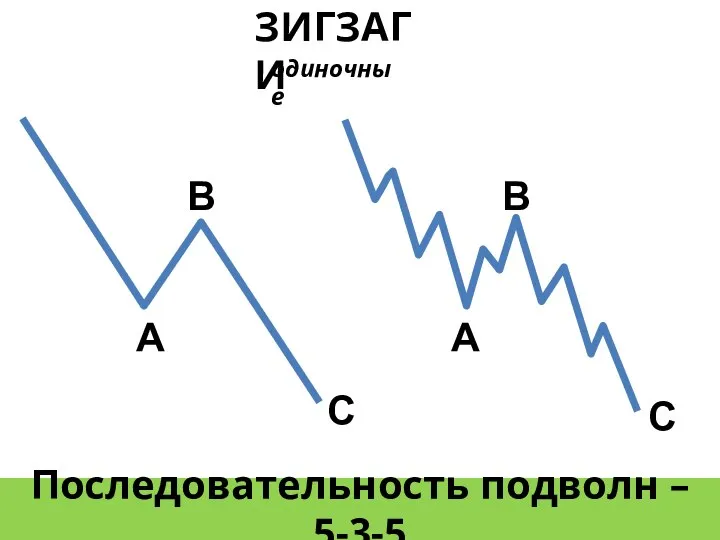
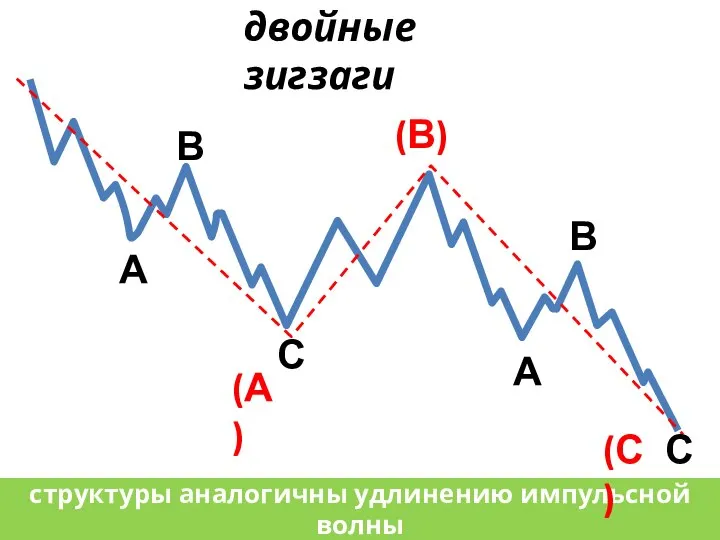
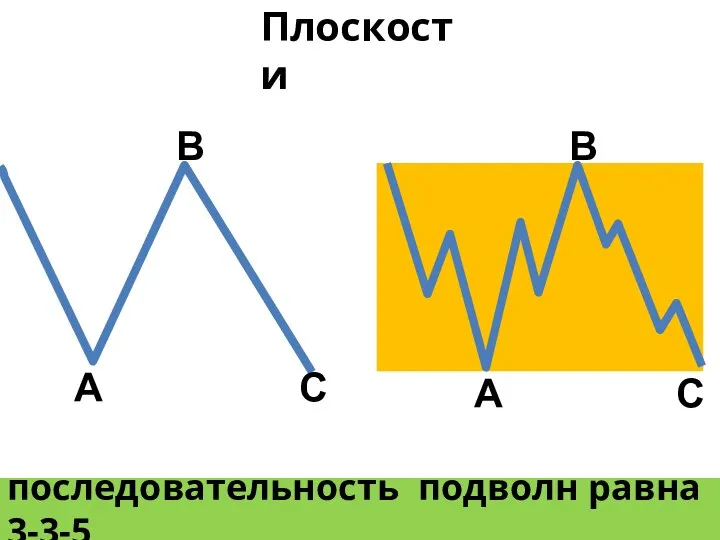
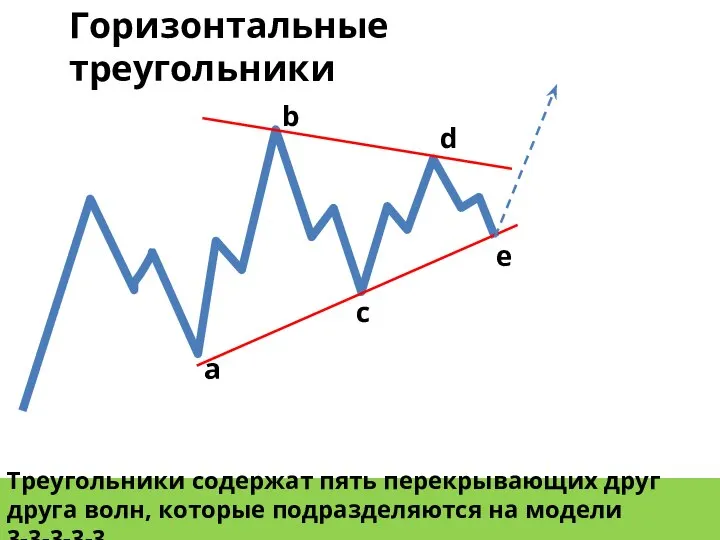
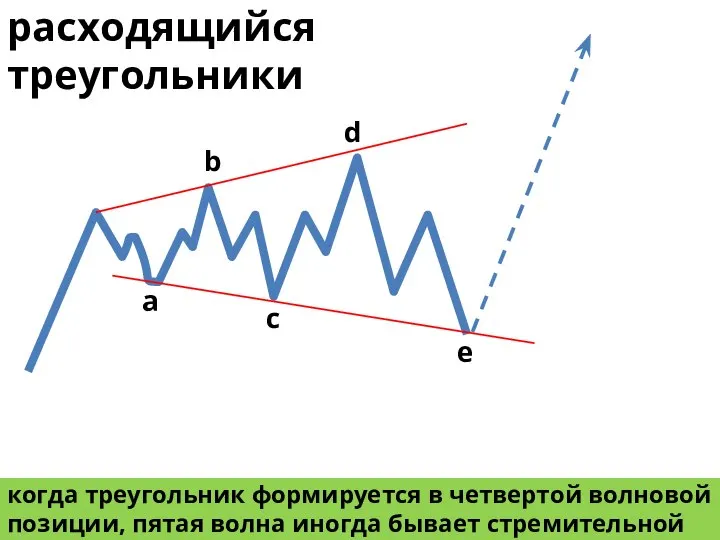
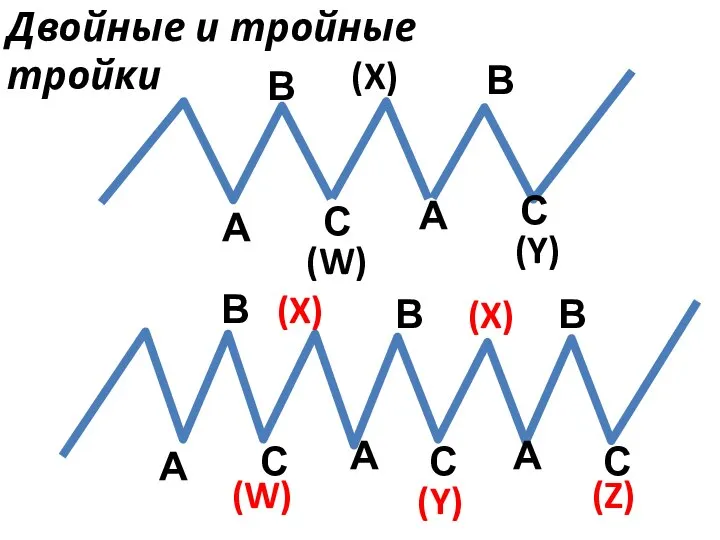
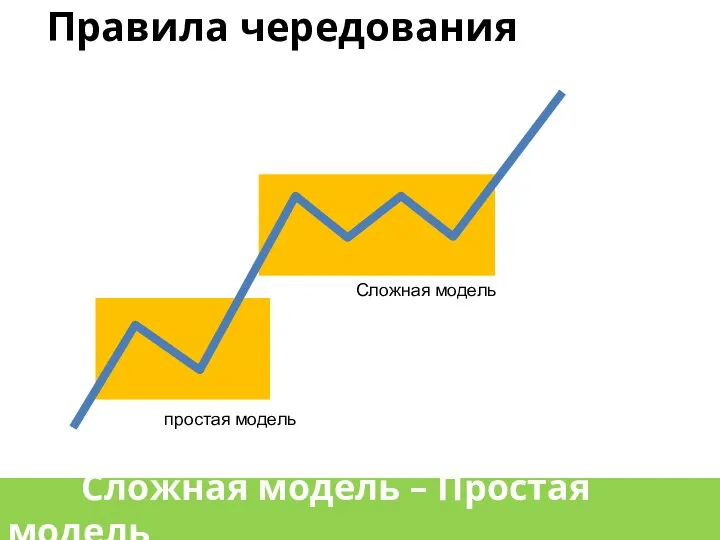

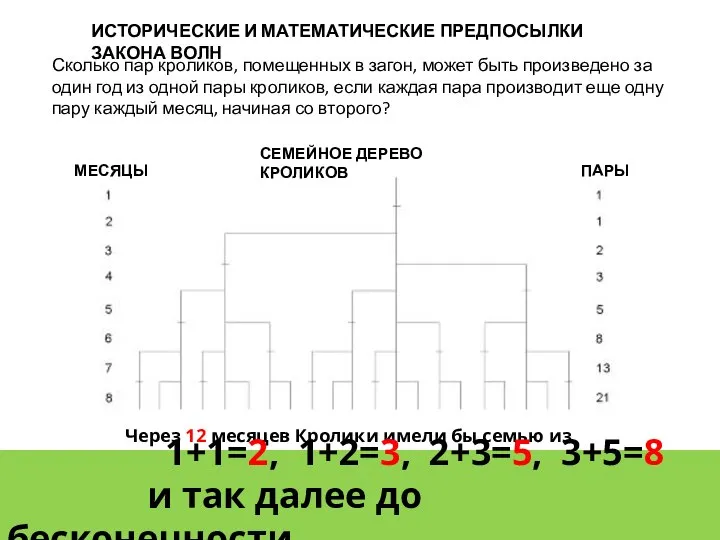
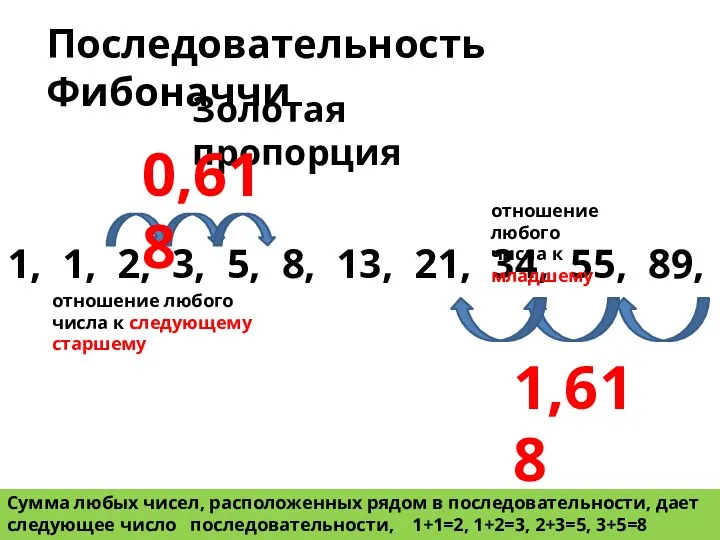
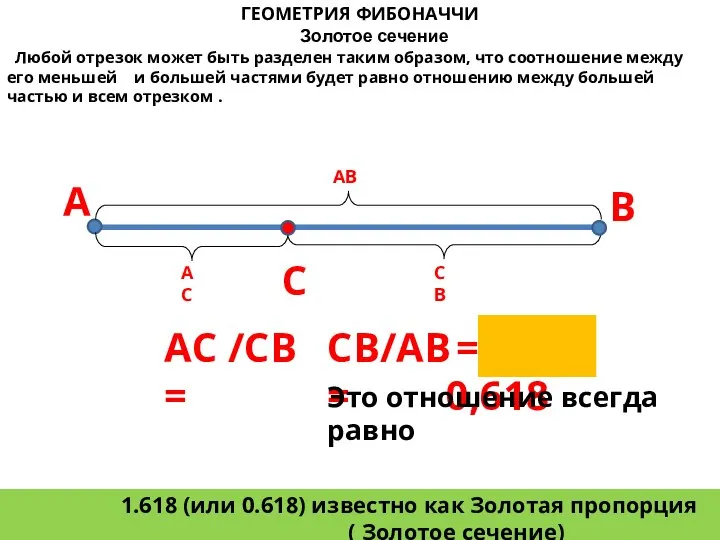
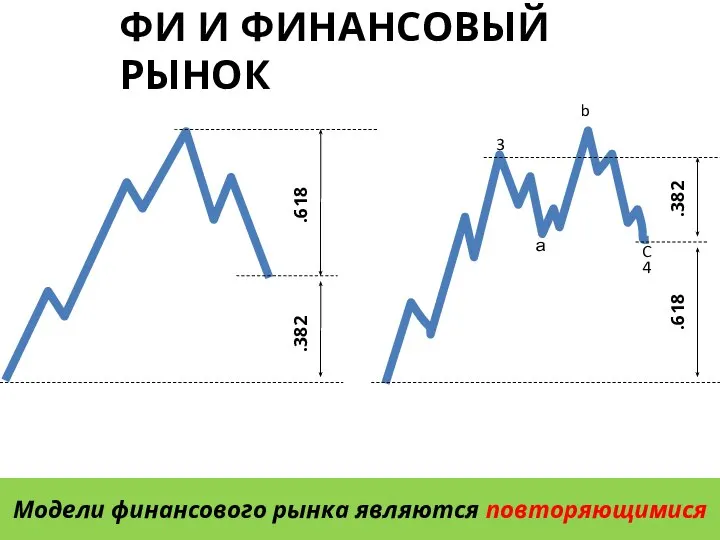
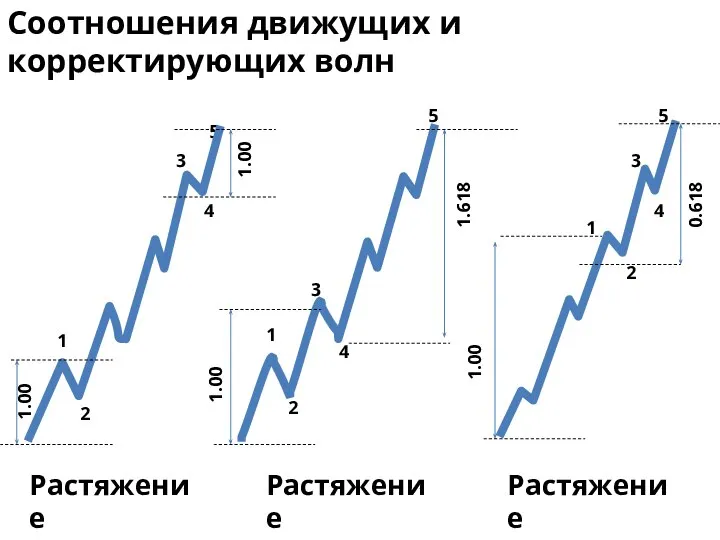
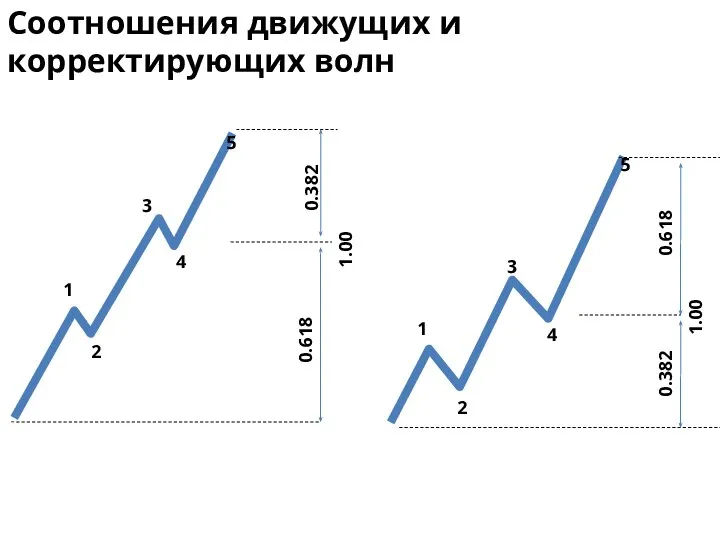



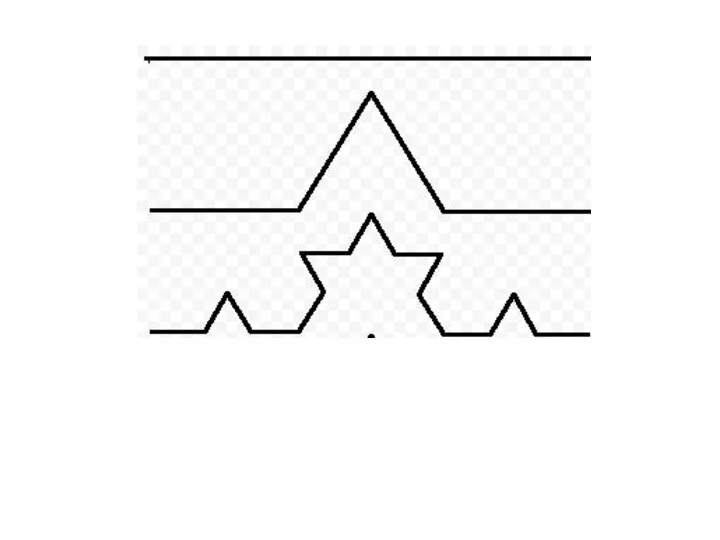
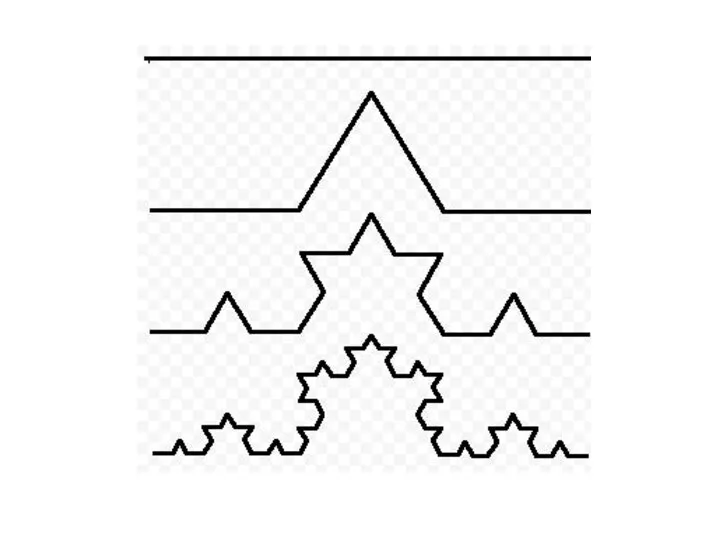


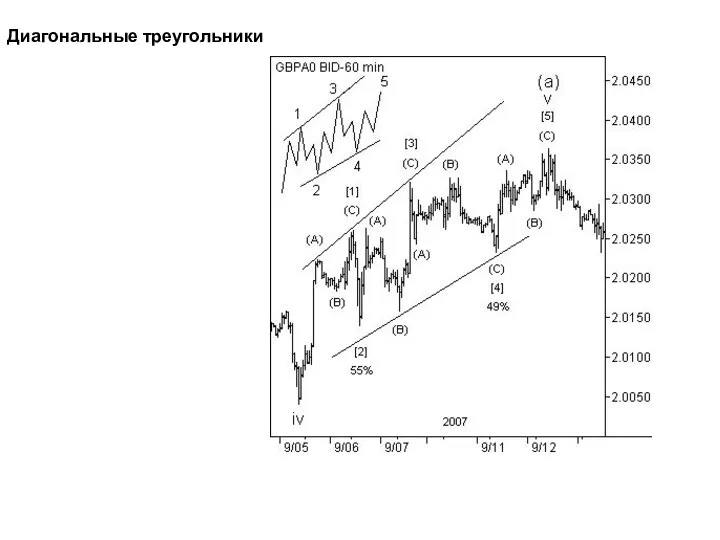
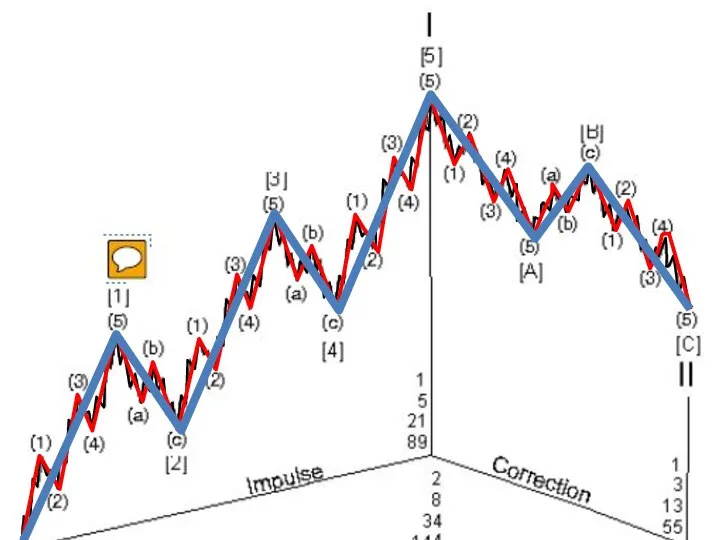



 График плавления и отвердевания кристаллических тел
График плавления и отвердевания кристаллических тел Аналоговая обработка сигналов
Аналоговая обработка сигналов Понятие о машине и механизме
Понятие о машине и механизме Физика в профессии: слесарь по ремонту автомобилей
Физика в профессии: слесарь по ремонту автомобилей Шу. Шудың түрлері; Шуды өлшеу әдісі. Алдын алу шаралары; Діріл
Шу. Шудың түрлері; Шуды өлшеу әдісі. Алдын алу шаралары; Діріл Инженерные решения
Инженерные решения Лекция №14. Интегралы, зависящие от параметров
Лекция №14. Интегралы, зависящие от параметров Магнитное поле. Лекция 20
Магнитное поле. Лекция 20 О времени и пространстве
О времени и пространстве Применение интеграла к решению физических задач
Применение интеграла к решению физических задач Презентация на тему Механические колебания (9 класс)
Презентация на тему Механические колебания (9 класс)  Магнитное поле проводника с током
Магнитное поле проводника с током Смесительный бак с регулированием уровня и температуры. Пример
Смесительный бак с регулированием уровня и температуры. Пример Статика. Устойчивое равновесие тел
Статика. Устойчивое равновесие тел Физика в самостоятельных исследованиях
Физика в самостоятельных исследованиях Тормозной путь автомобиля
Тормозной путь автомобиля Действие магнитного поля на движущийся электрический заряд
Действие магнитного поля на движущийся электрический заряд ентгенівське випромінювання, його застосування в медицині та техніці. Роботи І.Пулюя
ентгенівське випромінювання, його застосування в медицині та техніці. Роботи І.Пулюя Газовые законы
Газовые законы Теоретические основы электротехники. Теория электромагнитного поля. Лекция 8
Теоретические основы электротехники. Теория электромагнитного поля. Лекция 8 ВКР: Совершенствование процесса ТО автомобилей с разработкой системы вентиляции
ВКР: Совершенствование процесса ТО автомобилей с разработкой системы вентиляции Рация - переносное приёмо-передающее устройство
Рация - переносное приёмо-передающее устройство Нелинейные эффекты в средах с квадратичной нелинейностью. Лекция 2
Нелинейные эффекты в средах с квадратичной нелинейностью. Лекция 2 Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью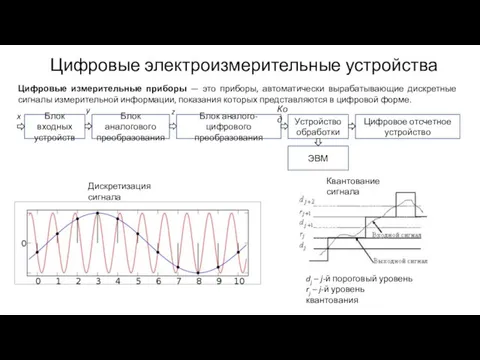 Цифровые электроизмерительные устройства
Цифровые электроизмерительные устройства Электрическое поле. Действие электрического поля на заряды. 8 класс
Электрическое поле. Действие электрического поля на заряды. 8 класс Что изучает физика
Что изучает физика Основы квантовой физики
Основы квантовой физики