Содержание
- 2. Лекция 1 Дифракция в кристаллах. Обратная решетка. Зоны Бриллюэна. Форм-фактор. Температурная зависимость линий отражения.
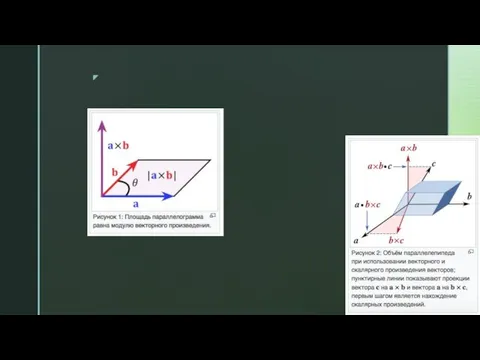
- 3. Векторные операции: скалярное и векторное произведение Скалярное произведение – операция над двумя векторами, результатом которой будет
- 4. Векторные операции: скалярное и векторное произведение
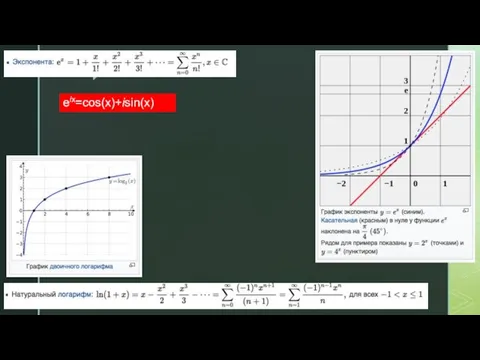
- 6. eix=cos(x)+isin(x)
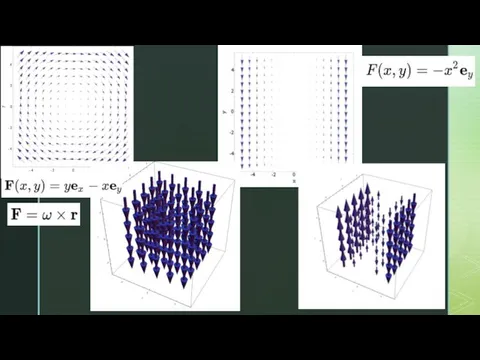
- 7. Градиентом скалярная функции называется векторная функция с компонентами. Ротор векторного поля дивергенция векторного поля, градиент
- 8. Ротор векторного поля дивергенция векторного поля, градиент rot (F) =▽xF Curl
- 10. ФF – поток векторного поля F через сферическую поверхность площадью S, ограничивающую объем V. Ротор векторного
- 12. Точечные группы симметрии обозначаются в символе Германа — Могена поворотные оси симметрии обозначают арабскими цифрами —
- 16. Решетки Браме: а – триклинная; б,в –моноклинные; г-ж – ромбические; з,и – тетрагональные; к – ромбоэдрическая;
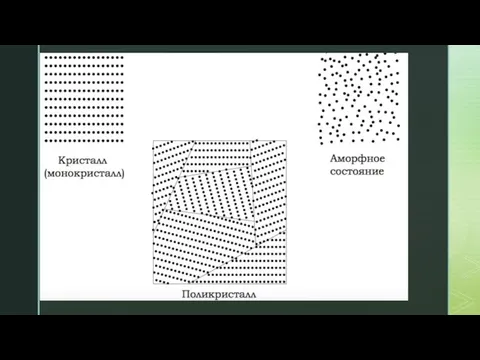
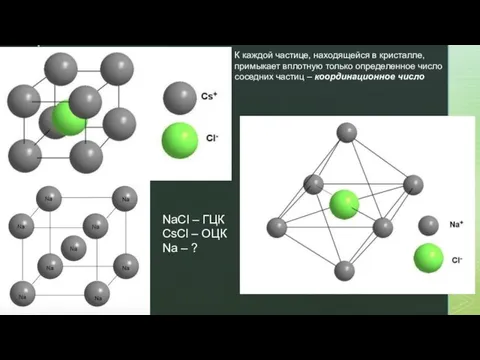
- 17. К каждой частице, находящейся в кристалле, примыкает вплотную только определенное число соседних частиц – координационное число
- 25. Дифракция фотонов, нейтронов и электронов X-Ray: λ, ε=hf, где h – постоянная Планка=6.62*10-34 Дж*сек Neutrons: длина
- 26. Дифракция фотонов, нейтронов и электронов
- 27. Закон Брегга-Вульфа (1913) Упругое рассеяние Может ли быть рассеяние на видимом свете? де-Бройля λ, ε=h2/2MNλ2, где
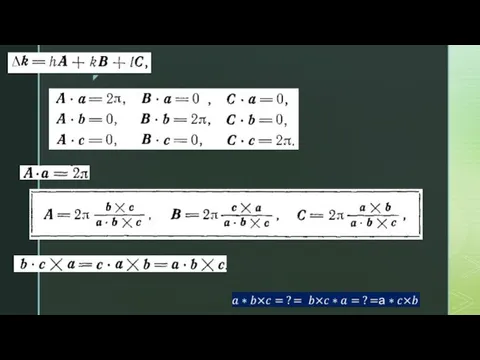
- 28. Обратная решетка
- 31. Фурье анализ периодических функций Концентрация электронов в кристалле n(ρ) где ρ - радиус вектор произвольной точки
- 32. Законы сохранения при рассеянии
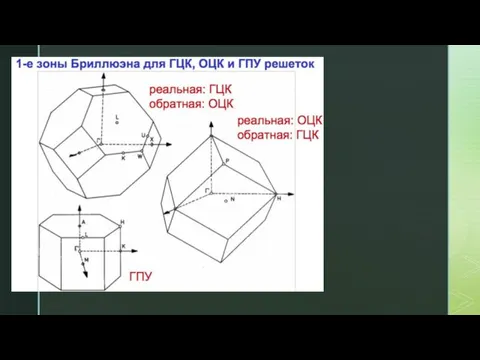
- 33. Построение Эвальда Правила отбора
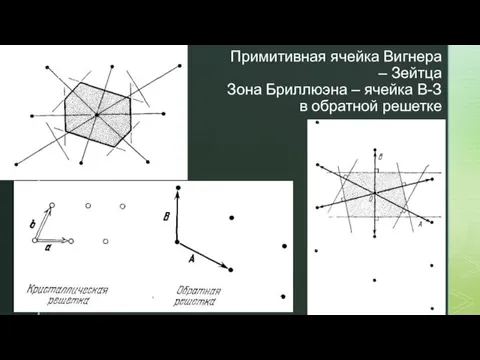
- 34. Примитивная ячейка Вигнера – Зейтца Зона Бриллюэна – ячейка В-З в обратной решетке
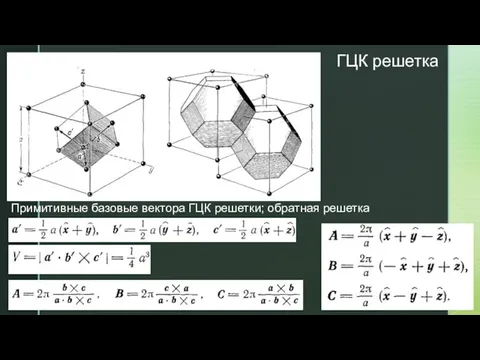
- 35. ГЦК решетка Примитивные базовые вектора ГЦК решетки; обратная решетка
- 37. Форм-фактор Условия дифракции Для отражения можно обозначить отражение как (hkl) и его интенсивность определяется плотностью электронных
- 39. eix=cos(x)+isin(x)
- 42. Атомный форм-фактор
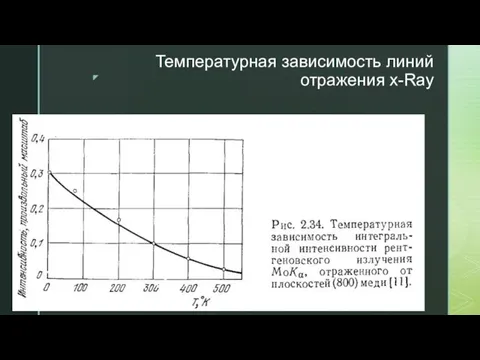
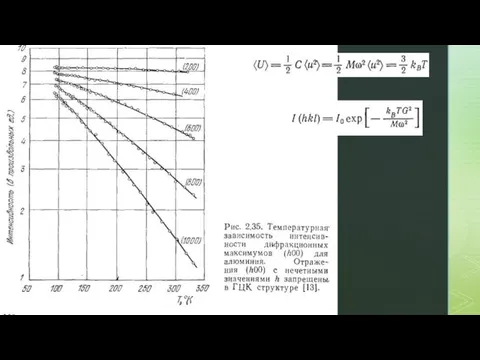
- 43. Температурная зависимость линий отражения x-Ray
- 44. Пусть положение атома в момент времени t задано как: Колебания случайные и независимые друг от друга
- 46. Дифракция Метод Лауэ Метод вращения кристалла Метод порошка Атомный форм-фактор Фактор Дебая-Уоллера Упругое и неупругое рассеяние
- 48. Скачать презентацию
































 Организация исследовательской деятельности школьников на уроках физики с использованием проблемного метода обучения
Организация исследовательской деятельности школьников на уроках физики с использованием проблемного метода обучения Зеркала
Зеркала Основы теории цифровой модуляции и детектирования
Основы теории цифровой модуляции и детектирования Назначение электрооборудования автомобиля КамАЗ-53215. Выполнение работ по замене стартера
Назначение электрооборудования автомобиля КамАЗ-53215. Выполнение работ по замене стартера Физика мыльных пузырей
Физика мыльных пузырей Урок 05 Сила Ампера
Урок 05 Сила Ампера Строение атома. Опыты Резерфорда
Строение атома. Опыты Резерфорда Флот начала XX века
Флот начала XX века Практическое применение электрического тока на примере электростимуляции растений
Практическое применение электрического тока на примере электростимуляции растений Температура и ее измерение
Температура и ее измерение Резерв
Резерв Низьковимірні системи
Низьковимірні системи Массообменные процессы
Массообменные процессы Презентация на тему Золотое правило механики (7 класс)
Презентация на тему Золотое правило механики (7 класс)  Тема 10. Схема устройства и принцип работы ПД
Тема 10. Схема устройства и принцип работы ПД 10.09.2022
10.09.2022 Основы постановки научного эксперимента. ЯМР-спектроскопия. (Лекция 8)
Основы постановки научного эксперимента. ЯМР-спектроскопия. (Лекция 8) Плоская система пар сил и условие её равновесия
Плоская система пар сил и условие её равновесия Презентация по физике "Передача и использование электроэнергии" -
Презентация по физике "Передача и использование электроэнергии" -  Поиск материалов с заданными свойствами. Практическая работа
Поиск материалов с заданными свойствами. Практическая работа Основы аэродинамики
Основы аэродинамики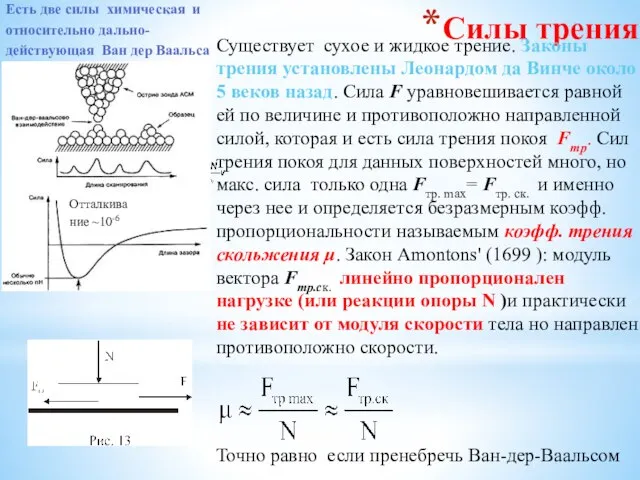 Силы трения
Силы трения Нормальные поля
Нормальные поля Задачи на определение показателей производственной программы и производственной мощности
Задачи на определение показателей производственной программы и производственной мощности Презентация на тему Агрегатное состояние вещества
Презентация на тему Агрегатное состояние вещества  Диэлектрики и проводники в электрическом поле
Диэлектрики и проводники в электрическом поле Физика вокруг нас
Физика вокруг нас Опыт Милликена. АФ1.4
Опыт Милликена. АФ1.4