Содержание
- 2. Повторение пройденного материала
- 3. Повторение пройденного материала
- 4. Изучение нового материала Перечень вопросов , подлежащих изучению 1.Сила тяжести как равнодействующая вертикальных сил. 2.Центр тяжести.
- 5. 1.Сила тяжести как равнодействующая вертикальных сил.
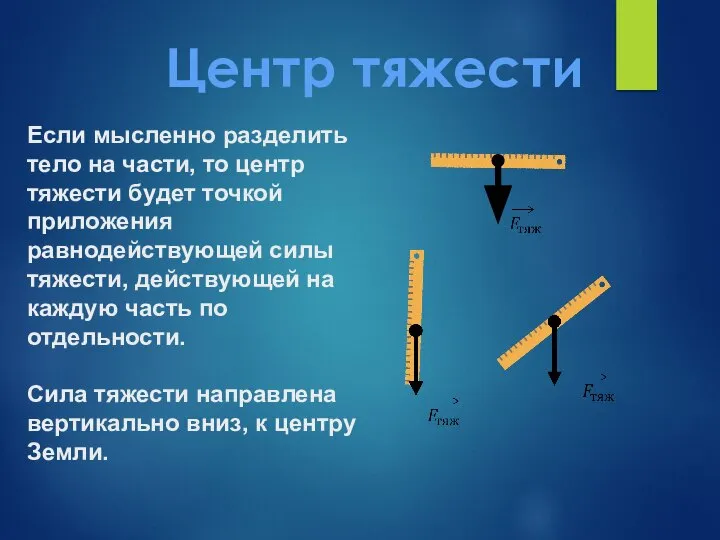
- 8. Если мысленно разделить тело на части, то центр тяжести будет точкой приложения равнодействующей силы тяжести, действующей
- 9. Устойчивость конструкций, механизмов – это необходимое условие при их эксплуатации. Таким образом, создавая машины и различные
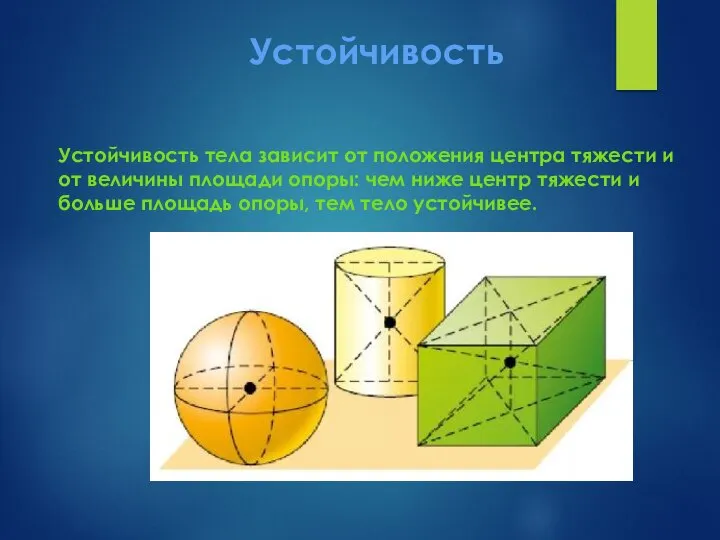
- 10. Устойчивость тела зависит от положения центра тяжести и от величины площади опоры: чем ниже центр тяжести
- 11. На примере опыта можно найти центр тяжести у плоского тела неправильной формы. Фигуру неправильной формы из
- 12. В каком равновесии находятся колёса машины? Колеса машины находятся в безразличном положении, так как ось вращения
- 13. В каком равновесии находится висящая под потолком люстра? Люстра находится в устойчивом равновесии, так как центр
- 14. Цирковые артисты в своих номерах для того, чтобы сохранять равновесие, смещают положение своего центра тяжести. Не
- 15. Сила тяжести – это сила, с которой тела притягиваются к земле Сила тяжести тела – это
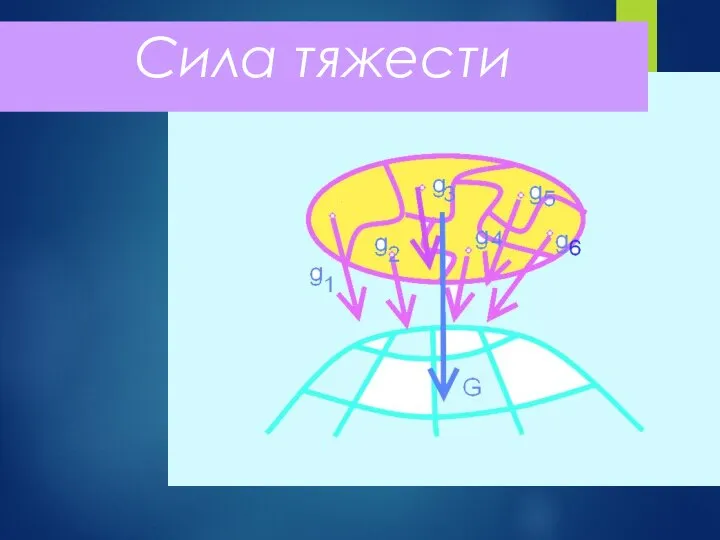
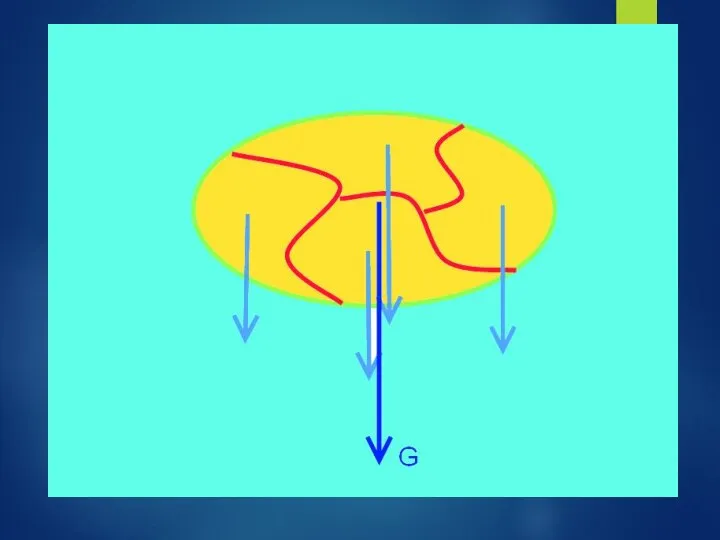
- 16. Сила тяжести
- 18. 2.Центр тяжести. Методы нахождения
- 19. Центр тяжести тела – это такая неизменно связанная с этим телом точка, через которую проходит линия
- 20. Методы определения центра тяжести тела - Способ подвешивания; - Способ взвешивания; - Аналитический способ.
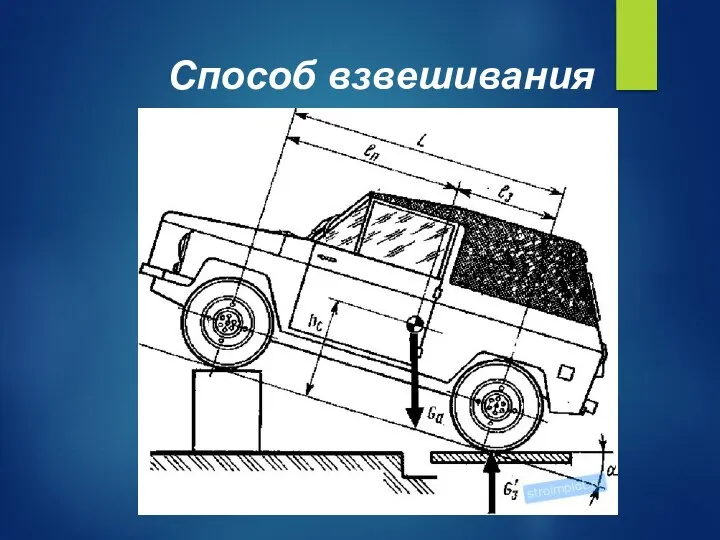
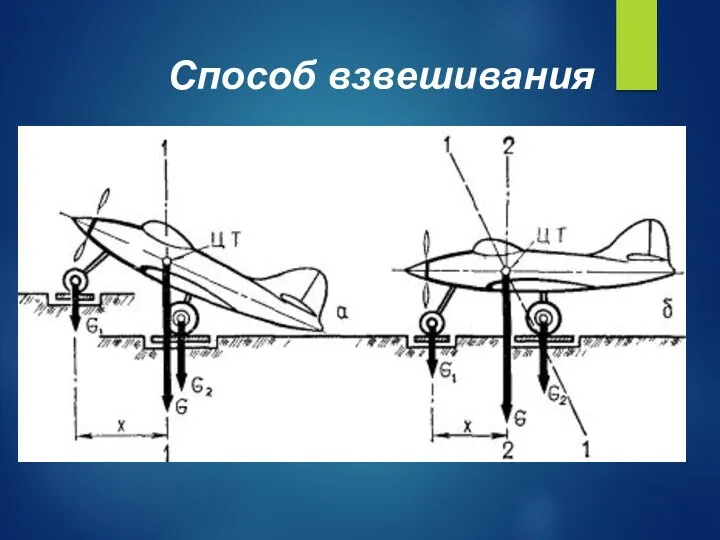
- 21. Способ взвешивания
- 22. Способ взвешивания
- 23. Аналитический способ 1 Метод симметрии 2 Метод разделения (разбиения) 3 Метод отрицательных масс
- 24. 1 Метод симметрии 1.1 Если однородное тело имеет плоскость симметрии, то центр тяжести лежит в этой
- 25. 1.2 Если однородное тело имеет ось симметрии, то центр тяжести лежит на этой оси. Центр тяжести
- 26. 2 Метод разделения (разбиения) Тело разбивается на наименьшее число частей, силы тяжести и положение центров тяжести
- 27. 3 Метод отрицательных масс При определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения,
- 28. Xc, Yc, Zc – координаты центра тяжести тела; Xi ,Yi , Zi – координаты i- ой
- 29. 3.Центр тяжести простых геометрических фигур
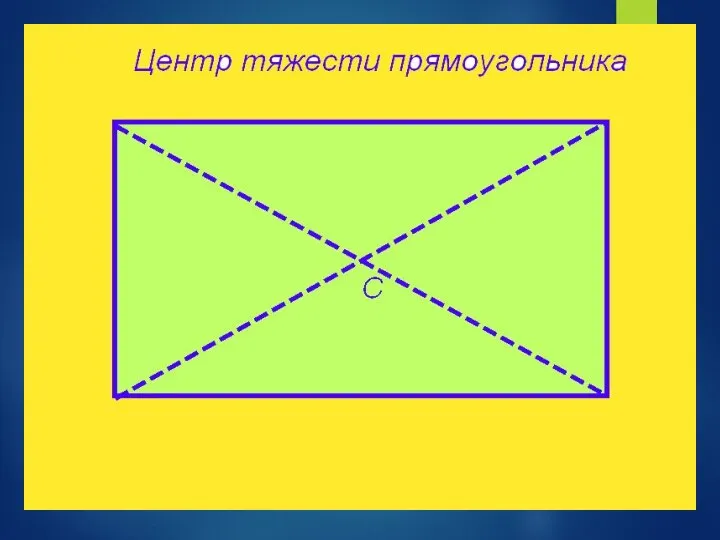
- 30. Координаты центра тяжести плоской фигуры
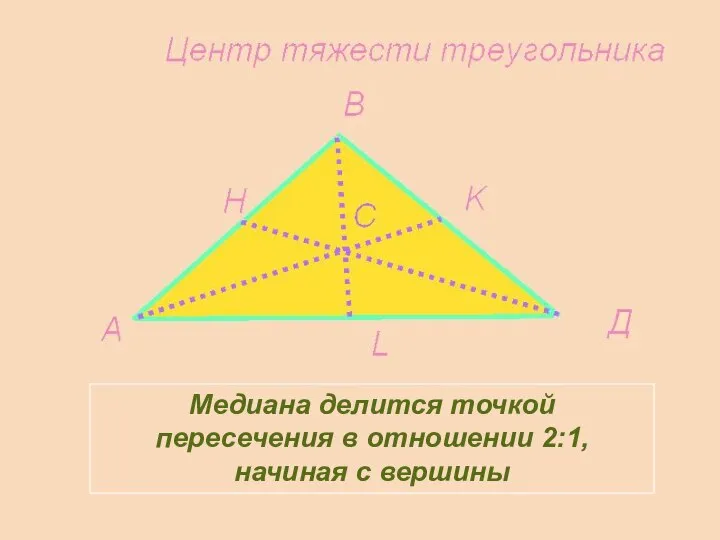
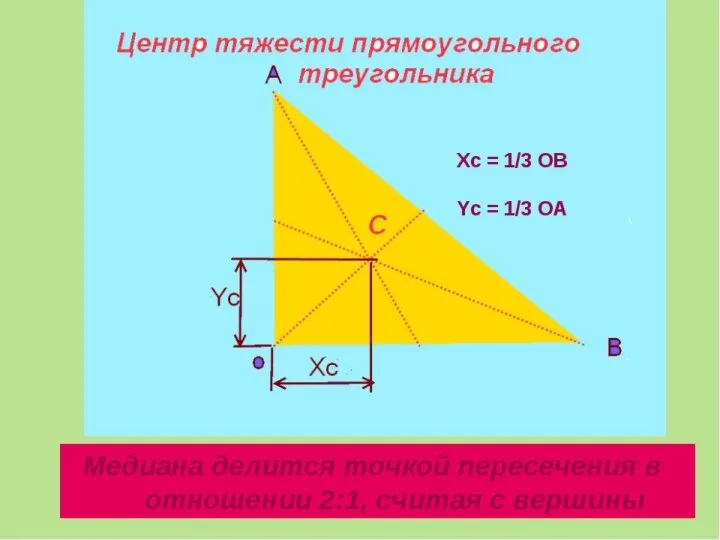
- 33. Медиана делится точкой пересечения в отношении 2:1, начиная с вершины
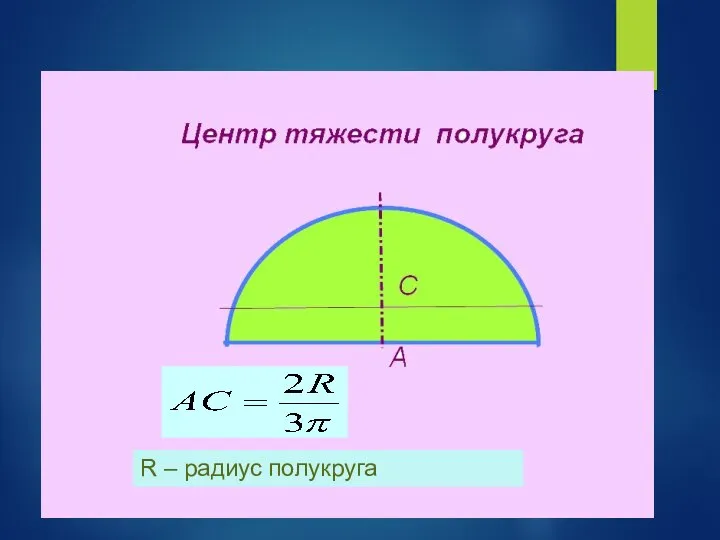
- 36. R – радиус полукруга
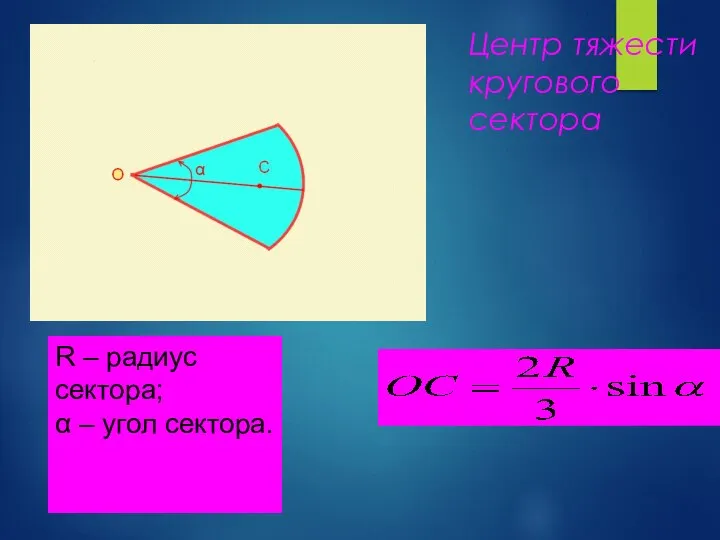
- 37. Центр тяжести кругового сектора R – радиус сектора; α – угол сектора.
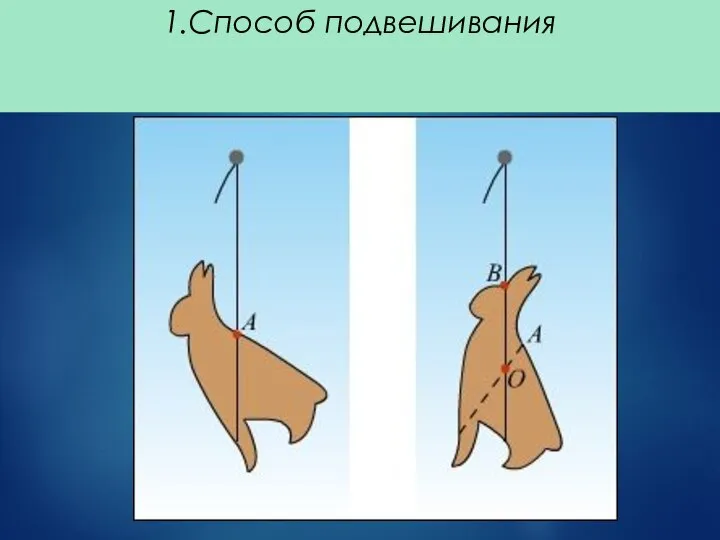
- 38. Определение центра тяжести фигуры неправильной формы. 1) Метод подвешивания на острие; 2) Теоретический метод
- 39. 1.Способ подвешивания
- 40. 2. Теоретический метод В этом случае сложная фигура разбивается на определенное количество элементарных фигур, имеющих правильную
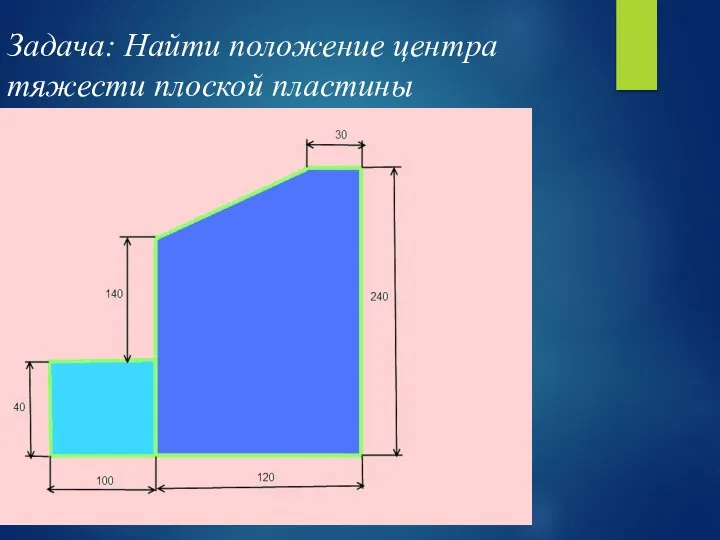
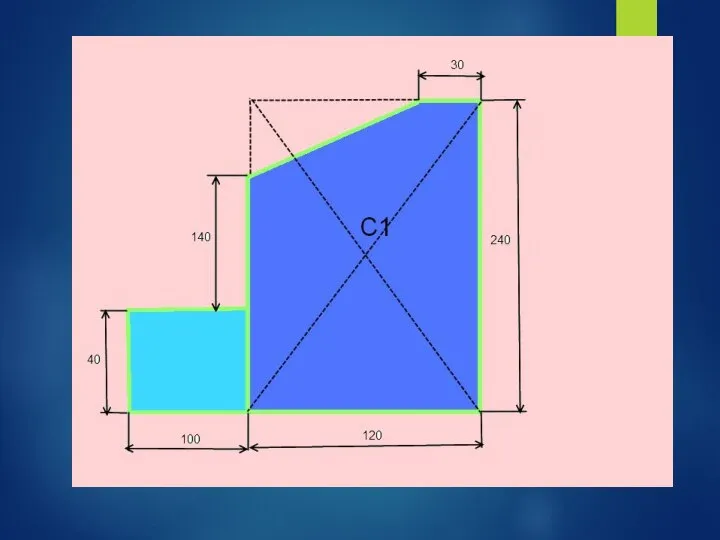
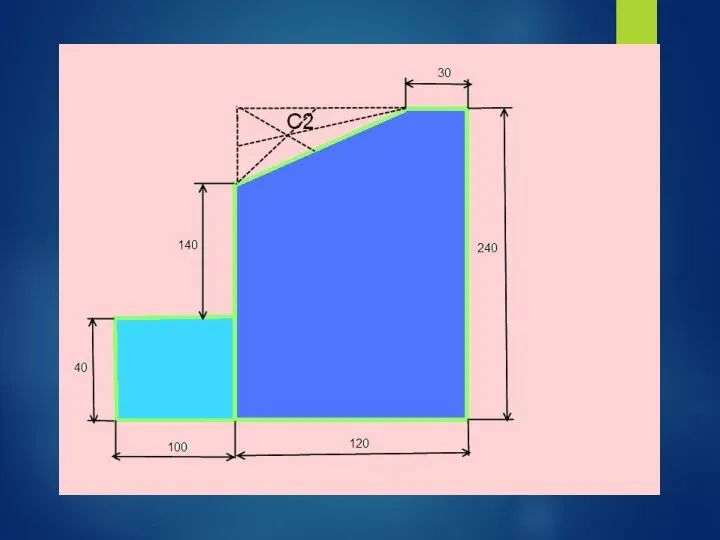
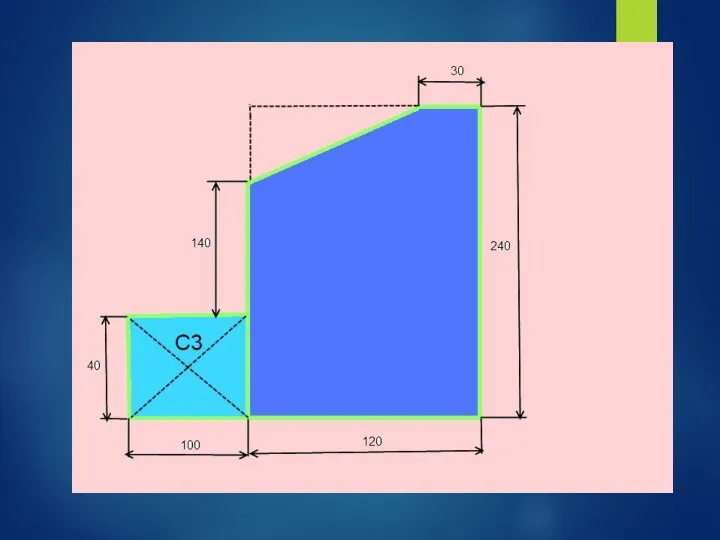
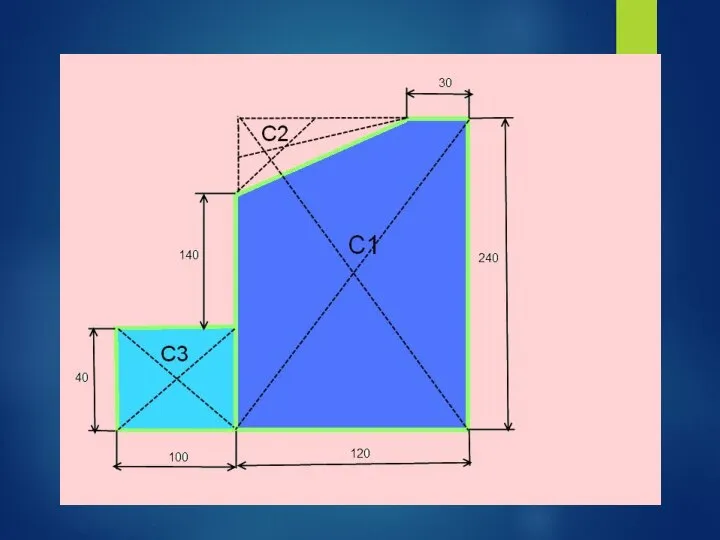
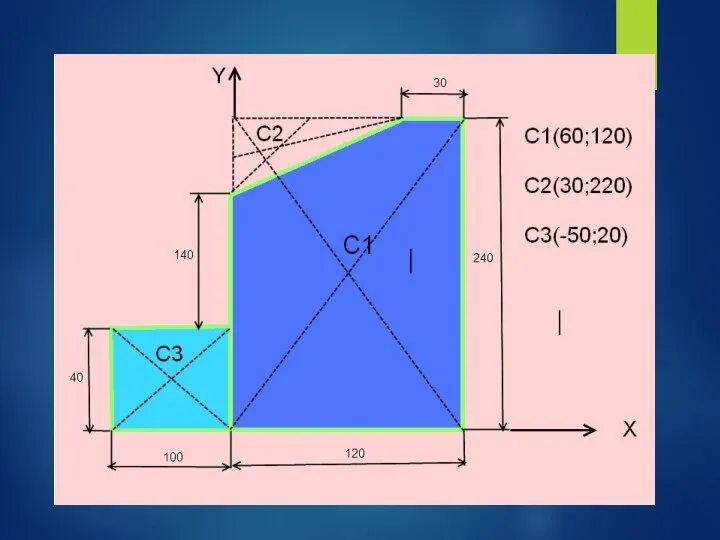
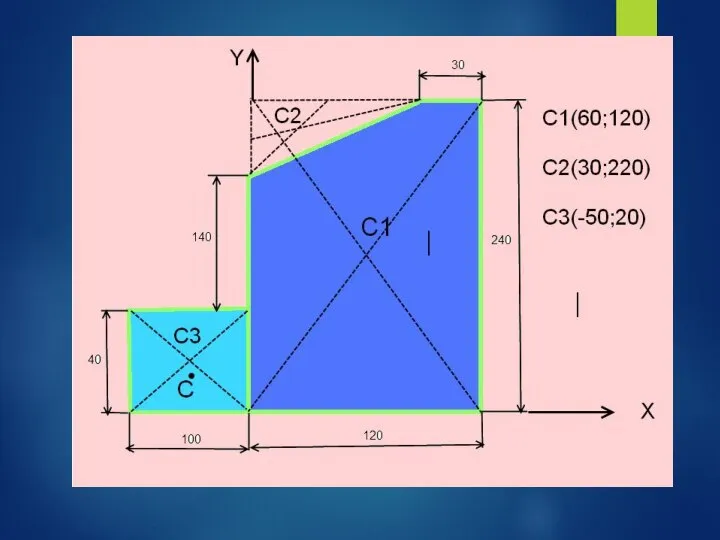
- 41. Задача: Найти положение центра тяжести плоской пластины
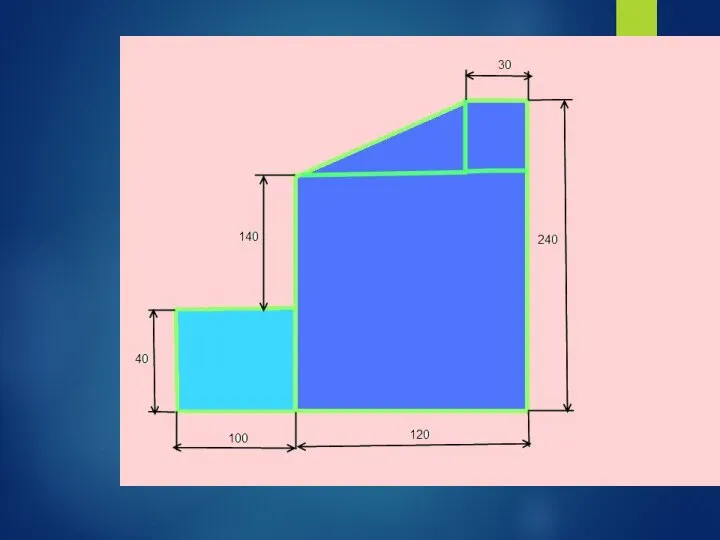
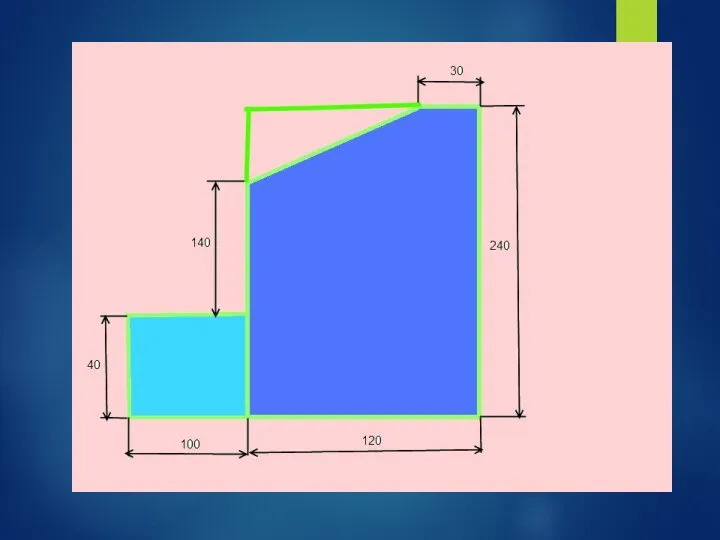
- 50. 1)Прямоугольник А1 = 10*4 = 40 см2 С1(6;12) 2) Прямоугольник А2 = 12*24 = 288 см2
- 51. 1)Прямоугольник А1 = 10*4 = 40 см2 С1(6;12) 2) Прямоугольник А2 = 12*24 = 288 см2
- 53. Закрепление изученного материала
- 54. Закрепление изученного материала
- 55. Закрепление изученного материала
- 56. Закрепление изученного материала
- 58. Скачать презентацию

































 Фотоэлементы: вакуумный и полупроводниковый
Фотоэлементы: вакуумный и полупроводниковый Электрические явления в природе: молнии
Электрические явления в природе: молнии Электромагнитная индукция. Опыты Фарадея
Электромагнитная индукция. Опыты Фарадея Статика
Статика Физические характеристики сигнала
Физические характеристики сигнала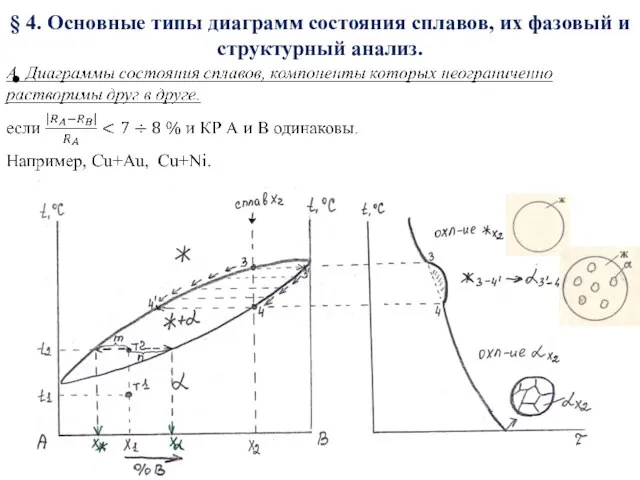 Диаграммы состояния сплавов, их фазовый и структурный анализ
Диаграммы состояния сплавов, их фазовый и структурный анализ Динамика и безопасность ядерных реакторов
Динамика и безопасность ядерных реакторов Шкала электромагнитных волн
Шкала электромагнитных волн Приемы выполнения фальцевого и заклепочного швов и соединения деталей
Приемы выполнения фальцевого и заклепочного швов и соединения деталей Тематический состав ВсОШ по физике для 10-ого класса
Тематический состав ВсОШ по физике для 10-ого класса Термодинамические функции газовых смесей. Идеальные растворы. Закон Рауля
Термодинамические функции газовых смесей. Идеальные растворы. Закон Рауля Устройство и работа ДВС (двигателя внутреннего сгорания)
Устройство и работа ДВС (двигателя внутреннего сгорания) Электрондық гармоникалық сигнал генераторлары Шаршы толқын генераторлары
Электрондық гармоникалық сигнал генераторлары Шаршы толқын генераторлары Электрические нагрузки. Графики электрических нагрузок. Режимы СЭС. Тема 2.1
Электрические нагрузки. Графики электрических нагрузок. Режимы СЭС. Тема 2.1 Электронные эффекты в молекулах органических соединений
Электронные эффекты в молекулах органических соединений Масса. Измерение массы
Масса. Измерение массы Последовательное соединение проводников
Последовательное соединение проводников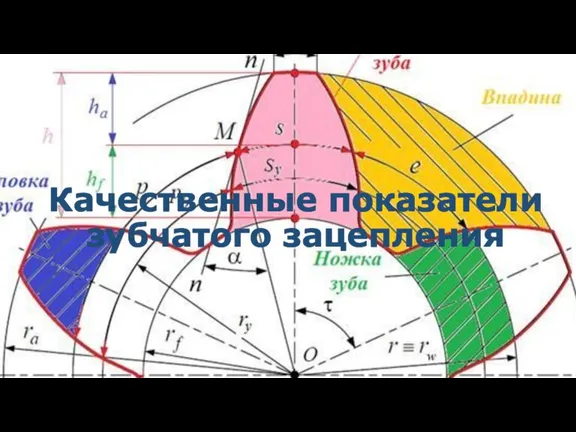 Качественные показатели зубчатого зацепления
Качественные показатели зубчатого зацепления Измерение температуры
Измерение температуры Урок-сказка: Первоначальные сведения о строении вещества 7 класс
Урок-сказка: Первоначальные сведения о строении вещества 7 класс Измерение механических величин
Измерение механических величин Инерциальная система отсчета
Инерциальная система отсчета Сверхпроводимость. ВТСП структуры
Сверхпроводимость. ВТСП структуры Геотермальная энергия
Геотермальная энергия Презентация на тему Спектры . Спектральный анализ. Спектральные аппараты
Презентация на тему Спектры . Спектральный анализ. Спектральные аппараты  Устройство микросамолёта R-20 Птенец-2
Устройство микросамолёта R-20 Птенец-2 Электромагнитные колебания. Превращение энергии в колебательном контуре
Электромагнитные колебания. Превращение энергии в колебательном контуре Влияние наушников на слух человека
Влияние наушников на слух человека