Содержание
- 2. Пространство и время в Ньютоновской механике Пространство 3 мерно Время независимо от пространства Размеры тел и
- 3. Уравнения механики не меняются при переходе из одной системы отсчета в другую Взаимодействие тел распространяется мгновенно
- 4. ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ
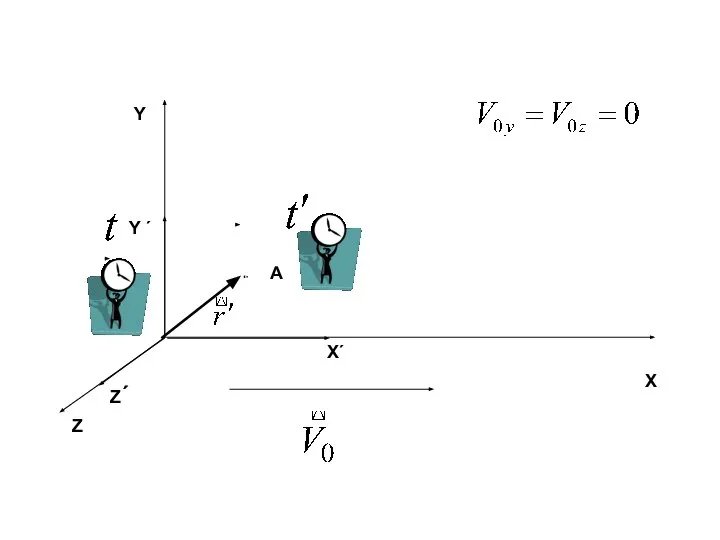
- 5. Y Z X
- 6. ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ
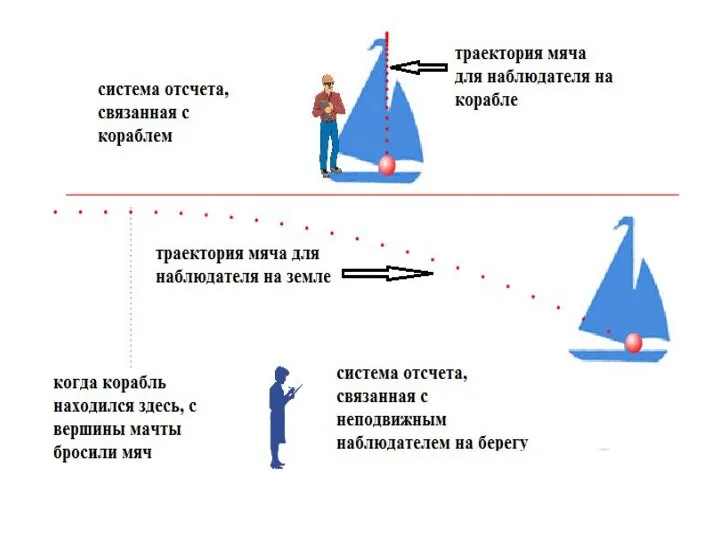
- 8. Принцип относительности Галилея Все законы механики имеют одинаковую форму во всех инерциальных системах отсчета
- 10. ПОСТУЛАТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ (ПОСТУЛАТЫ ЭЙНШТЕЙНА) Все законы физики не меняются при переходе от одной инерциальной системы
- 11. Синхронизация часов Для описания события необходимо указать место и время Чтобы корректно описывать время в различных
- 12. Одновременность событий зависит от системы отсчета В ньютоновской механике это достигалось за счет мгновенного распространения сигнала
- 13. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА Линейная связь между координатой и временем При малых скоростях должны переходить в преобразования Галилея
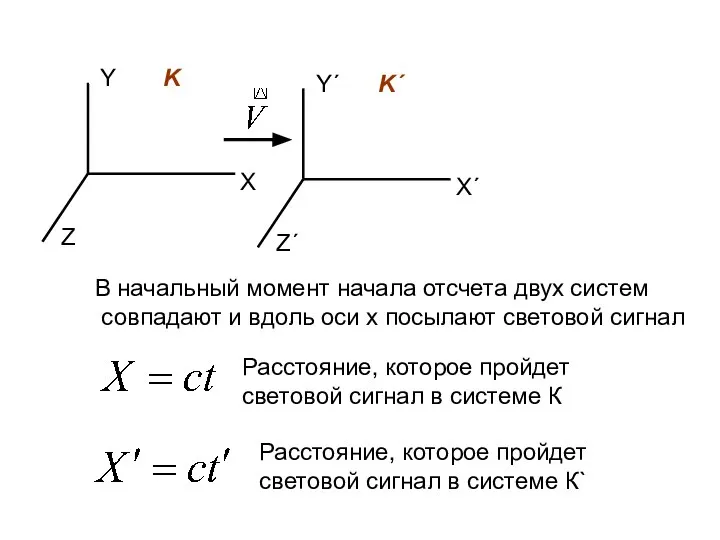
- 14. Х Y Z K Х΄ Y΄ Z΄ K΄ В начальный момент начала отсчета двух систем совпадают
- 19. Преобразования К ́́–К и К- К ́́ симметричны, отличаются знаком Время течет по-разному в различных системах
- 20. СЛЕДСТВИЯ ИЗ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- 21. Понятие одновременности Пусть в системе К происходят два события А (x1,y1,z1,t1) B (x2,y2,z2,t2) Найдем промежуток времени
- 23. Если события одновременны в одной системе отсчета Совсем не обязательно одновременны в другой
- 24. ЕСЛИ СОБЫТИЯ ОДНОМЕСТНЫ И ОДНОВРЕМЕННЫ В ОДНОЙ СИСТЕМЕ ОТСЧЕТА , ТО ОНИ ОДНОВРЕМЕННЫ В ЛЮБОЙ ДРУГОЙ
- 25. Пусть в некоторой покоящейся точке системы К происходит событие длительностью Δt Найдем длительность этого события в
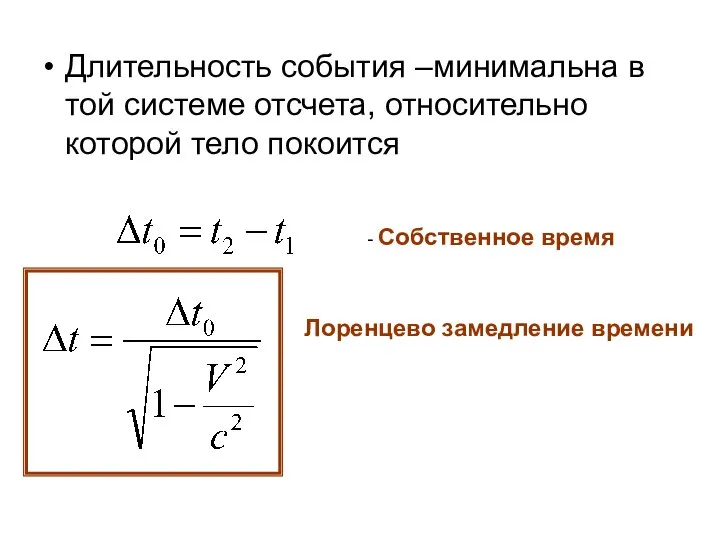
- 27. Длительность события –минимальна в той системе отсчета, относительно которой тело покоится - Собственное время Лоренцево замедление
- 28. ПРИМЕР РАСПАД ПИОНА Π-мезон – положительно заряженная частица Время жизни пиона в системе отсчета , где
- 29. С точки зрения пиона он пройдет до распада расстояние
- 31. ДЛИНА ТЕЛ В РАЗЛИЧНЫХ СИСТЕМАХ ОТСЧЕТА Пусть стержень покоится в системе К΄ и расположен вдоль оси
- 34. В системе отсчета, относительно которой стержень покоится его длина называется собственной и максимальна В движущихся относительно
- 35. Релятивистский закон сложения скоростей
- 36. Пусть в К системе отсчета частица движется со скоростью Найдем проекции скорости в системе К ́
- 44. Скачать презентацию




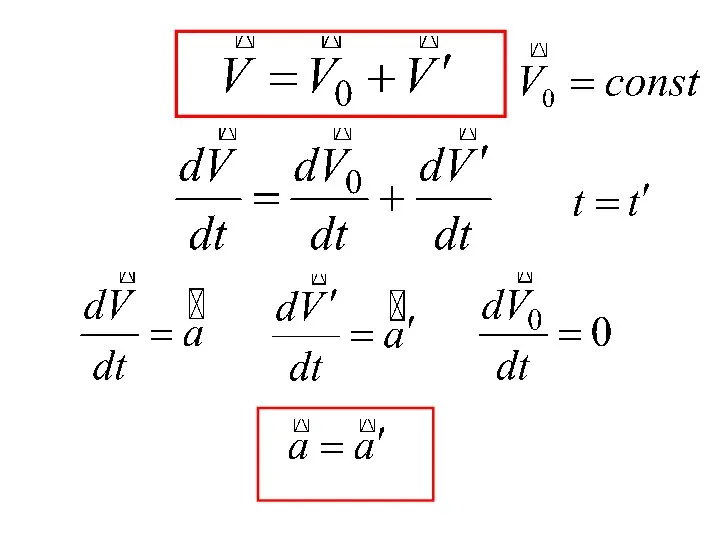





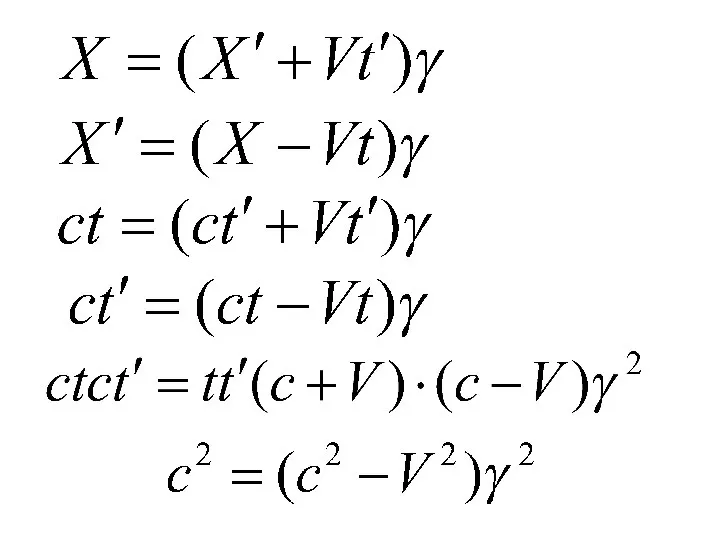
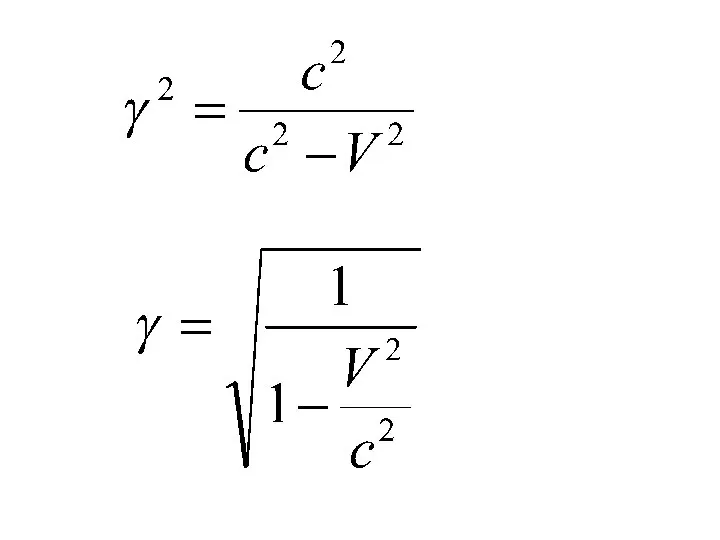
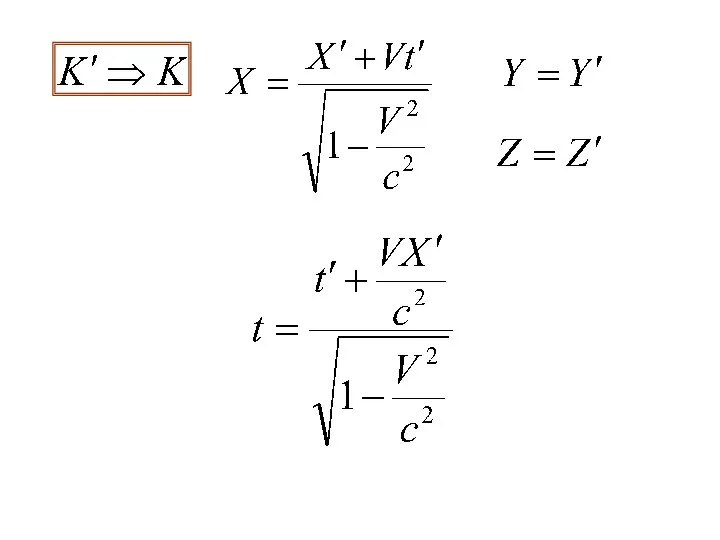
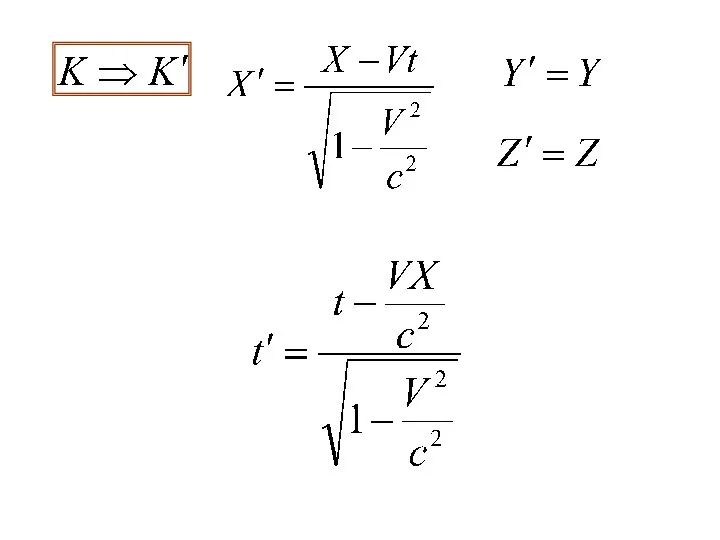



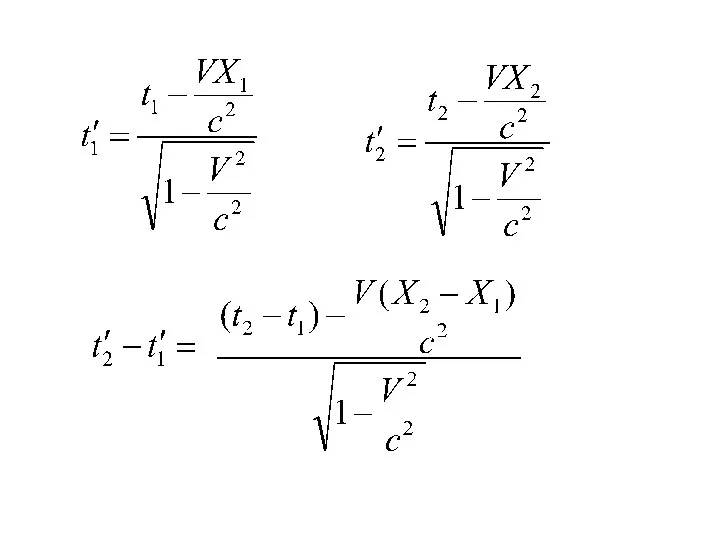



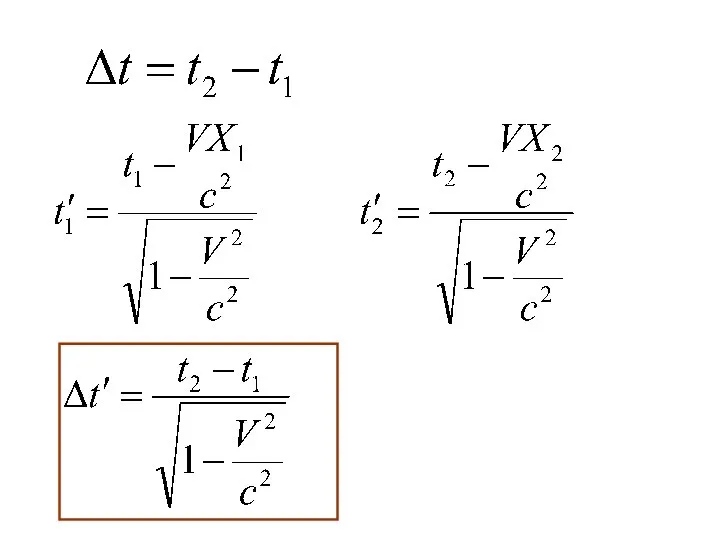


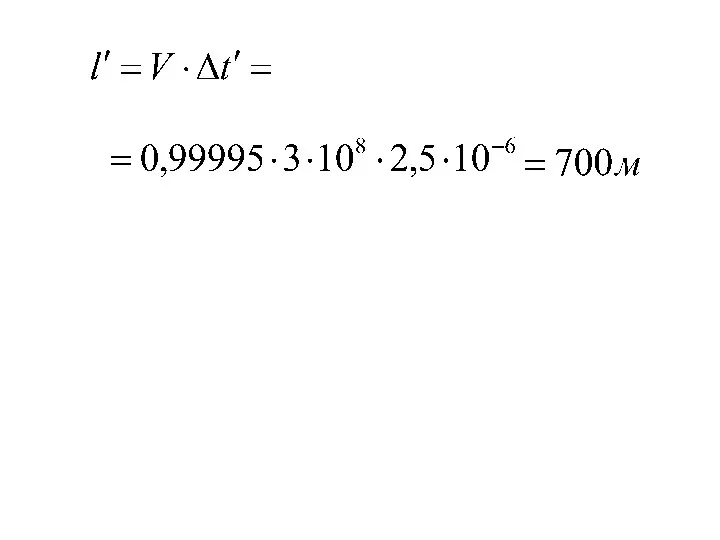

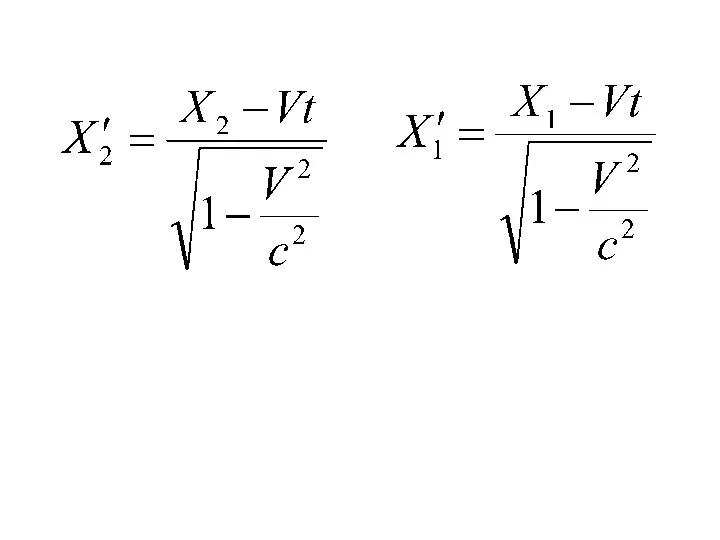
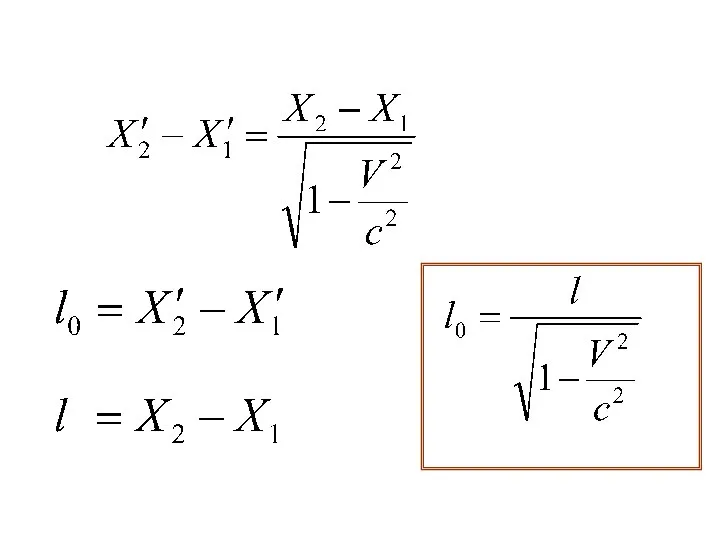



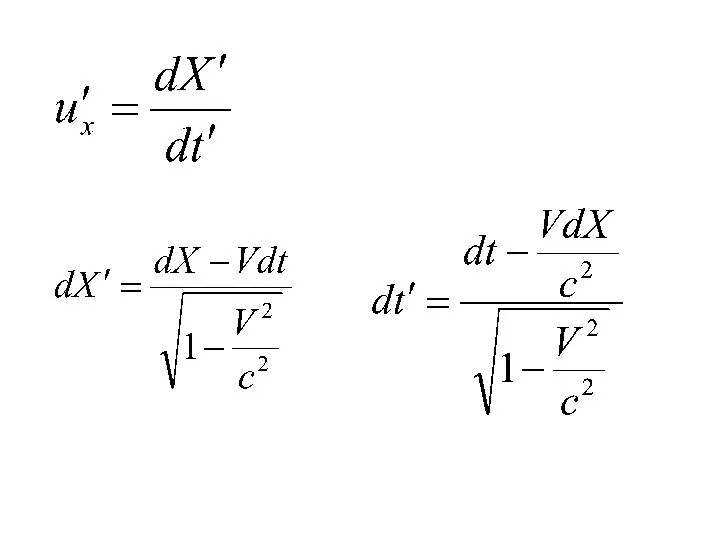
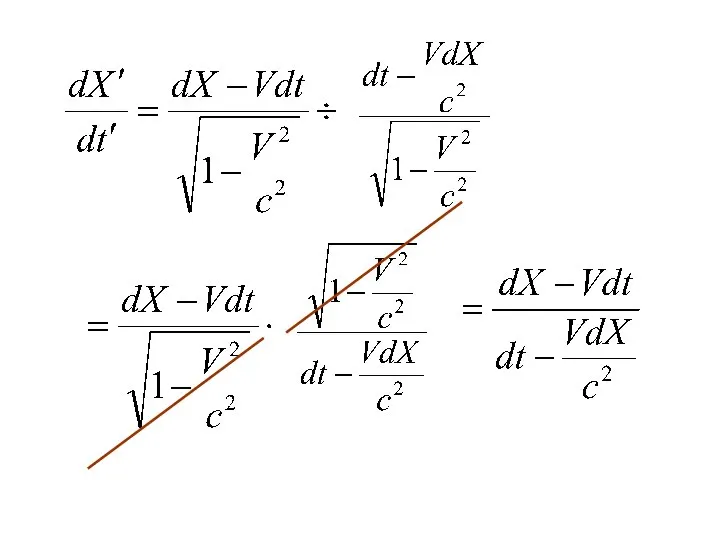
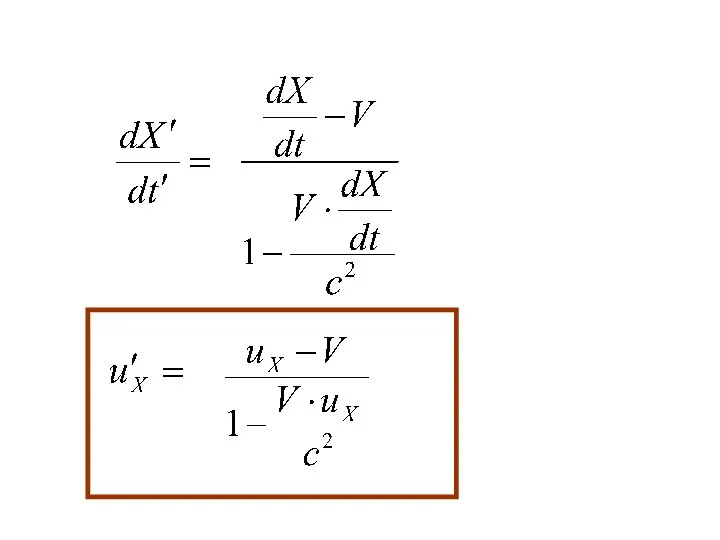
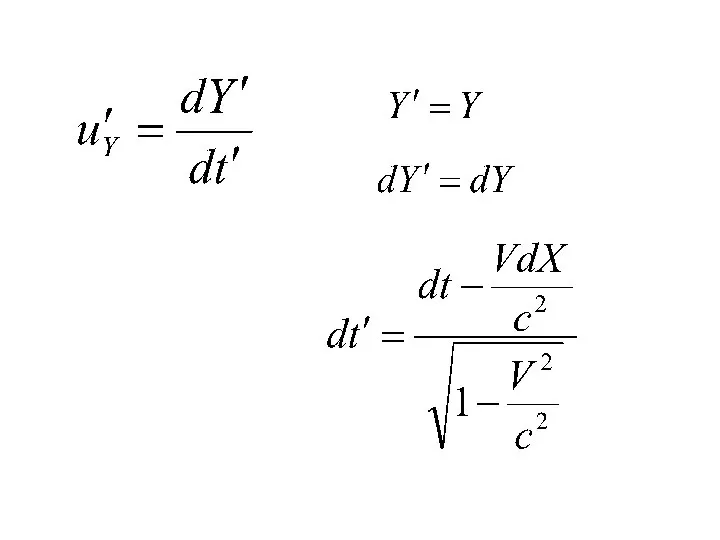
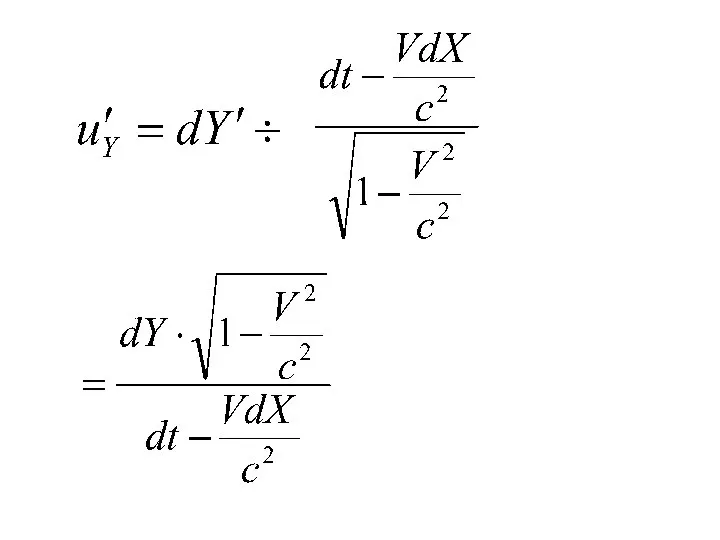

 Принцип относительности Галилея. Инвариантные и относительные физические величины
Принцип относительности Галилея. Инвариантные и относительные физические величины Выпускная бакалаврская работа Повышение безопасности труда при ремонте сельскохозяйственной техники
Выпускная бакалаврская работа Повышение безопасности труда при ремонте сельскохозяйственной техники Виды гидравлических сопротивлений
Виды гидравлических сопротивлений Исследование радиотехнической системы контроля положения нарушителя
Исследование радиотехнической системы контроля положения нарушителя Стоячие волны Урок физики в 10 классе (естественно-научный профиль) © Автор Богданова Ирина Викторовна
Стоячие волны Урок физики в 10 классе (естественно-научный профиль) © Автор Богданова Ирина Викторовна Презентация на тему Генерирование переменного электрического тока
Презентация на тему Генерирование переменного электрического тока  Постоянные магниты
Постоянные магниты Примеры наклонной плоскости
Примеры наклонной плоскости Выбор резисторов
Выбор резисторов Гармонические колебания. Амплитуда, период и частота колебательного движения
Гармонические колебания. Амплитуда, период и частота колебательного движения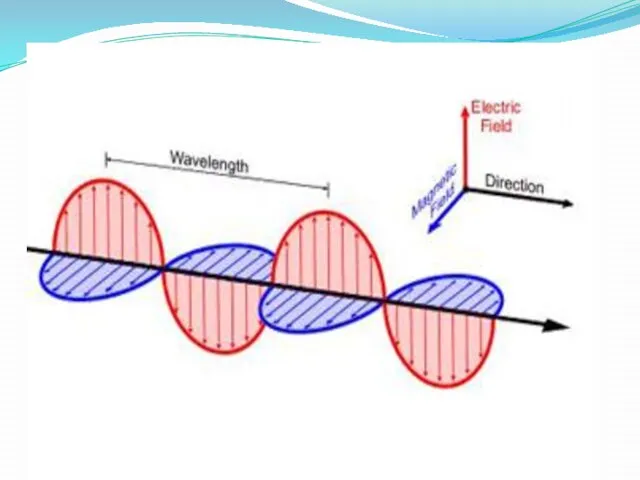 Микронометр
Микронометр Особенности частотного планирования сотовых сетей цифровой радиосвязи
Особенности частотного планирования сотовых сетей цифровой радиосвязи Делящиеся материалы. Тема 5
Делящиеся материалы. Тема 5 Как создать суперкар и решить задачи, возникающие при его создании
Как создать суперкар и решить задачи, возникающие при его создании Пузырьковая камера
Пузырьковая камера Применение аккумуляторов. 8 класс
Применение аккумуляторов. 8 класс Волновые явления
Волновые явления Виды теплопередачи
Виды теплопередачи Диагностика технического состояния рулевого управления автомобиля Ниссан Альмера
Диагностика технического состояния рулевого управления автомобиля Ниссан Альмера Трубчатый ферментёр
Трубчатый ферментёр Основы МКТ идеального газа. Тренировочный тест
Основы МКТ идеального газа. Тренировочный тест Презентация на тему Оптические иллюзии или обман зрения
Презентация на тему Оптические иллюзии или обман зрения  Магнитные материалы. Гистерезис. Применение ферромагнитных материалов
Магнитные материалы. Гистерезис. Применение ферромагнитных материалов Линзы. Построение изображений в линзах
Линзы. Построение изображений в линзах Масс-спектрометрия
Масс-спектрометрия Первое начало термодинамики. Виды теплообмена
Первое начало термодинамики. Виды теплообмена Механика деформируемого твердого тела
Механика деформируемого твердого тела Ядерный реактор. Получение радиоактивных изотопов и их применение
Ядерный реактор. Получение радиоактивных изотопов и их применение