Содержание
- 2. INHALT Einleitung: Definitionen, Werkstoffgruppen, Physikalische Eigenschaften Metalle Legierungen Eisenlegierung
- 3. DEFINITION: WERKSTOFFKUNDE
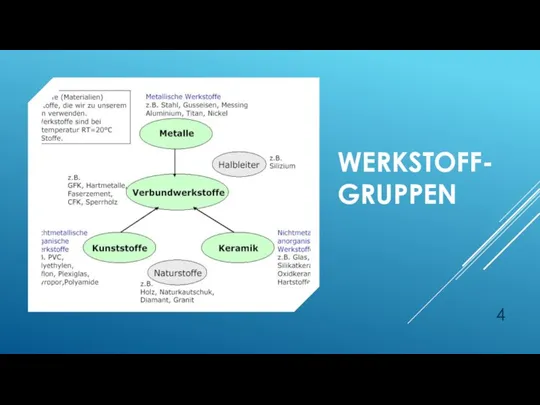
- 4. WERKSTOFF-GRUPPEN
- 5. Bekanntester Vertreter aus dieser Gruppe ist … mit seinen Legierungen ……… und …….. Zu den metallischen
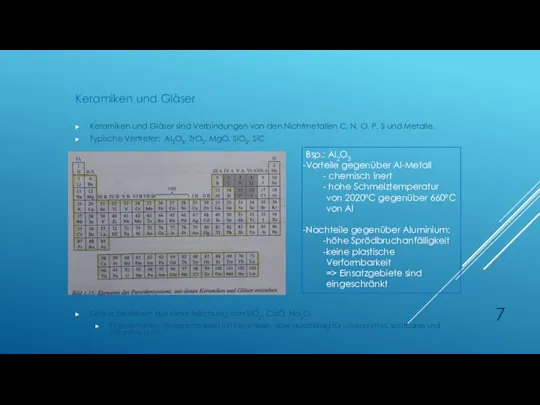
- 7. Keramiken und Gläser sind Verbindungen von den Nichtmetallen C, N, O, P, S und Metalle. Typische
- 8. Keramiken sind wie Metalle ………. aufgebaut, d.h. in einem bestimmten Gitter Gläser dagegen besitzen eine …………..
- 9. bestehen aus Nichtmetallen. Das Grundgerüst ist immer eine …………………………- Kette die übrigen Nichtmetalle findet man z.B.
- 10. VERBUNDWERKSTOFFE VW entstehen durch Kombination von unterschiedlichen/unterschiedlich strukturierten Werkstoffen aus einer oder mehreren Werkstoffhauptgruppen Ziel: …………
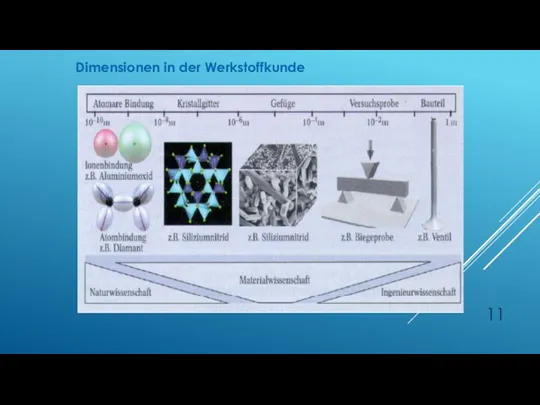
- 11. Dimensionen in der Werkstoffkunde
- 12. Nach Abwägung aller Gesichtspunkte wird für ein Bauteil der Werkstoff ausgewählt, der die Funktion des Bauteils
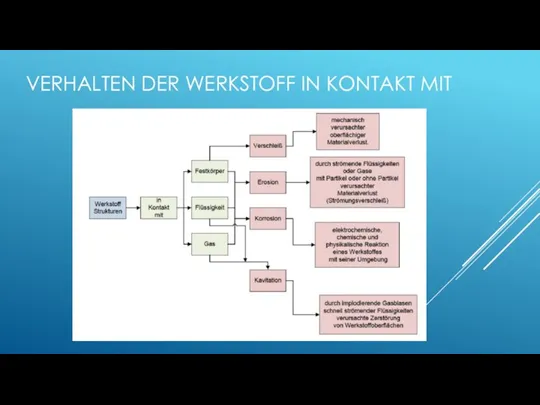
- 13. VERHALTEN DER WERKSTOFF IN KONTAKT MIT
- 14. Schmelzpunkt (Schmelztemperatur) Elektrische Leitfähigkeit Physikalische Eigenschaften der Werkstoffe
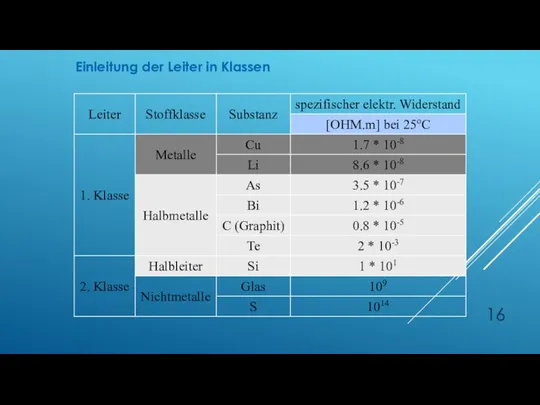
- 15. Leiter 1. Klasse (z. B.. Metalle oder Halbmetalle), bei denen eine Temperaturerhöhung zu einer Verringerung der
- 16. Einleitung der Leiter in Klassen
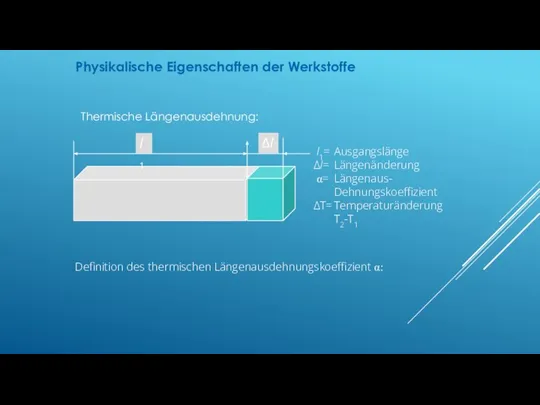
- 17. l1= Ausgangslänge Δl= Längenänderung α= Längenaus- Dehnungskoeffizient ΔT= Temperaturänderung T2-T1 Definition des thermischen Längenausdehnungskoeffizient α: Physikalische
- 18. Wärmeleitfähigkeit Definition der Wärmeleitfähigkeit: Physikalische Eigenschaften der Werkstoffe
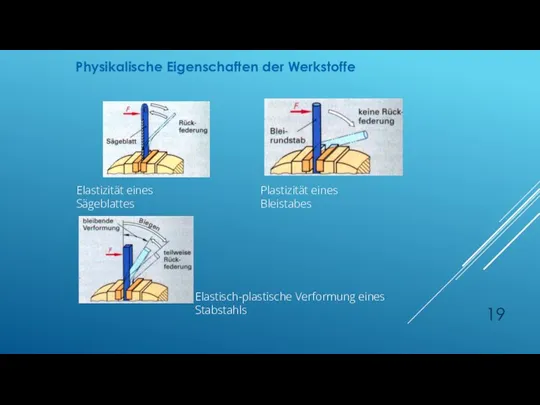
- 19. Elastizität eines Sägeblattes Plastizität eines Bleistabes Elastisch-plastische Verformung eines Stabstahls Physikalische Eigenschaften der Werkstoffe
- 20. INHALT Einleitung: Definitionen, Werkstoffgruppen, Physikalische Eigenschaften Metalle Kristallzustand der Metalle Legierungskunde – Zustandsdiagramme Kristallplastizität Diffusion Kristallerholung
- 21. METALLE - ALLGEMEIN Typische Metalle Eigenschaften sind:
- 22. METALLE – KRISTALLZUSTAND DER METALLE - LERNZIELE Das Raumgitter als Idealstruktur bestimmt viele Eigenschaften und Vorgänge
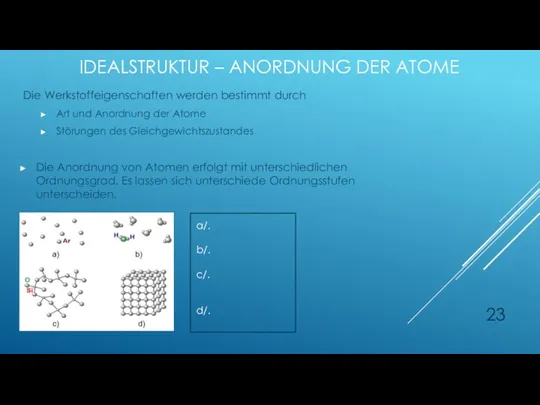
- 23. IDEALSTRUKTUR – ANORDNUNG DER ATOME Die Werkstoffeigenschaften werden bestimmt durch Art und Anordnung der Atome Störungen
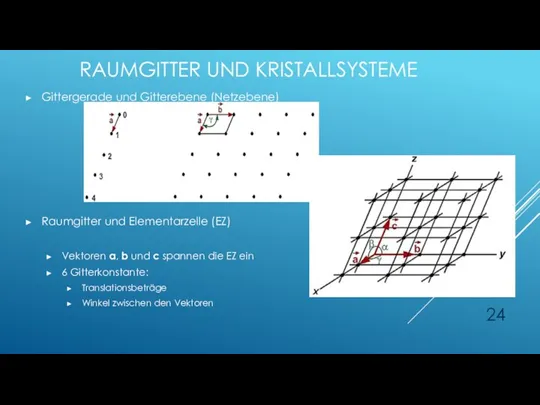
- 24. RAUMGITTER UND KRISTALLSYSTEME Gittergerade und Gitterebene (Netzebene) Raumgitter und Elementarzelle (EZ) Vektoren a, b und c
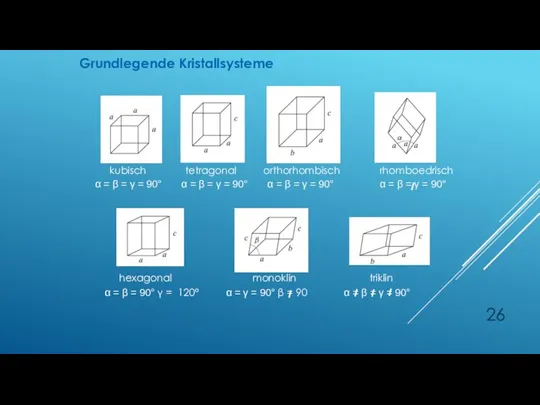
- 25. RAUMGITTER UND KRISTALLSYSTEME 7 Kristallsysteme Definition einer EZ
- 26. kubisch tetragonal orthorhombisch rhomboedrisch hexagonal monoklin triklin α = β = γ = 90° α =
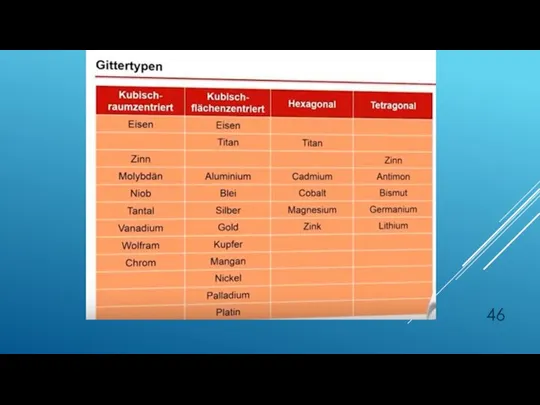
- 27. GITTERAUFBAU Gitteraufbau der Metalle (Legierungen) wird durch die Angabe der EZ und Ihrer Größe charakterisiert. Die
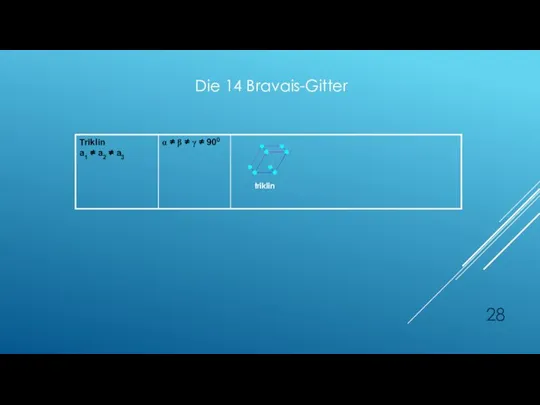
- 28. triklin Die 14 Bravais-Gitter
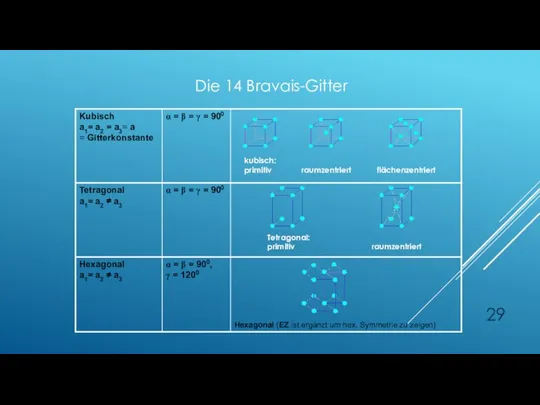
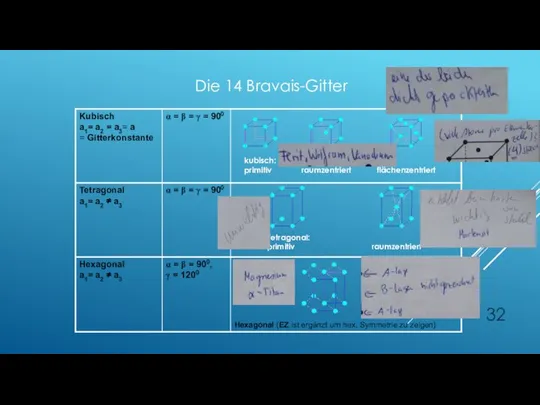
- 29. kubisch: primitiv raumzentriert flächenzentriert Tetragonal: primitiv raumzentriert Die 14 Bravais-Gitter
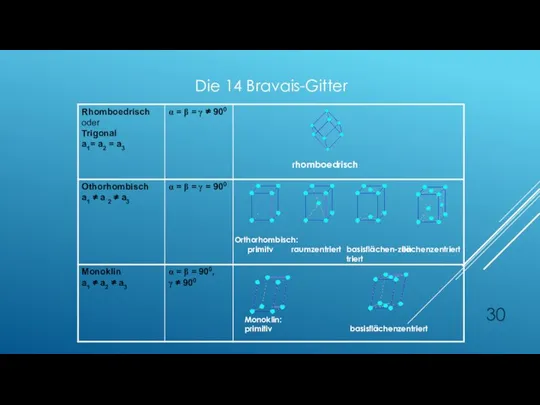
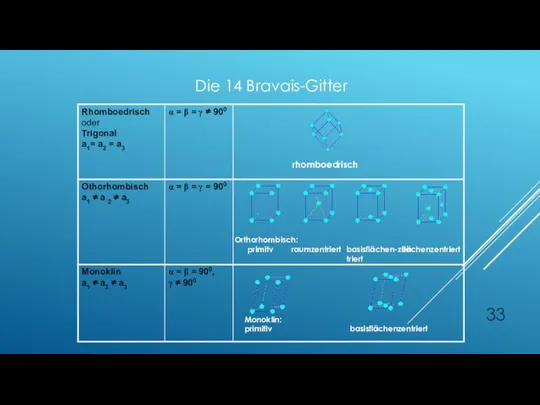
- 30. rhomboedrisch Orthorhombisch: primitv raumzentriert basisflächen-zentriert flächenzentriert Monoklin: primitiv basisflächenzentriert Die 14 Bravais-Gitter
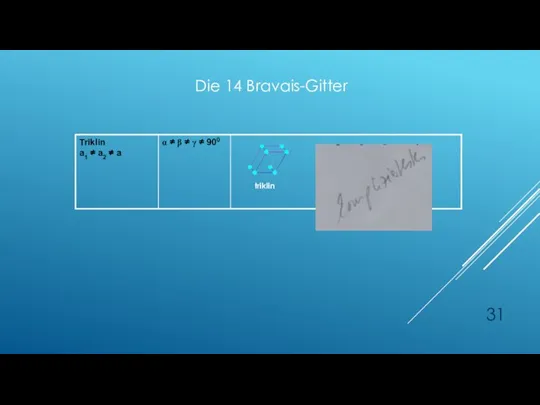
- 31. triklin Die 14 Bravais-Gitter
- 32. kubisch: primitiv raumzentriert flächenzentriert Tetragonal: primitiv raumzentriert Die 14 Bravais-Gitter
- 33. rhomboedrisch Orthorhombisch: primitv raumzentriert basisflächen-zentriert flächenzentriert Monoklin: primitiv basisflächenzentriert Die 14 Bravais-Gitter
- 34. KENNGRÖSSEN DER KRZ-EZ Beispiel KZ des kubisch-primitiven Kristalls:
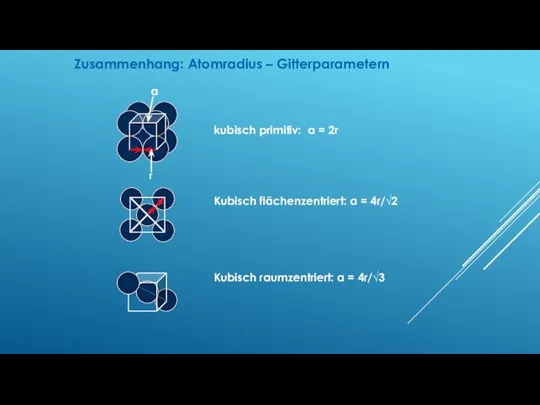
- 35. Zusammenhang: Atomradius – Gitterparametern kubisch primitiv: a = 2r Kubisch flächenzentriert: a = 4r/√2 Kubisch raumzentriert:
- 36. kubisch-flächenzentrierte ElementarzellePackungsdichte kubisch-raumzentrierte Elementarzelle Packungsdichte – kubische Gitter ?
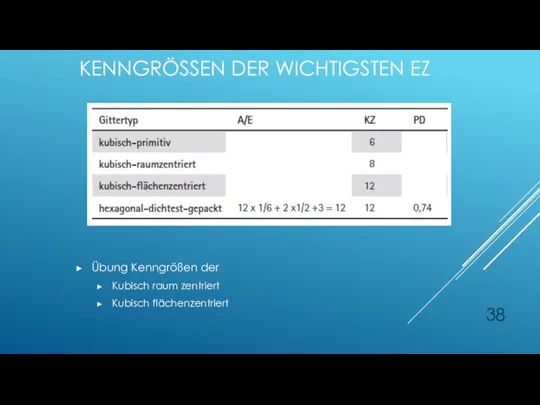
- 38. KENNGRÖSSEN DER WICHTIGSTEN EZ Übung Kenngrößen der Kubisch raum zentriert Kubisch flächenzentriert
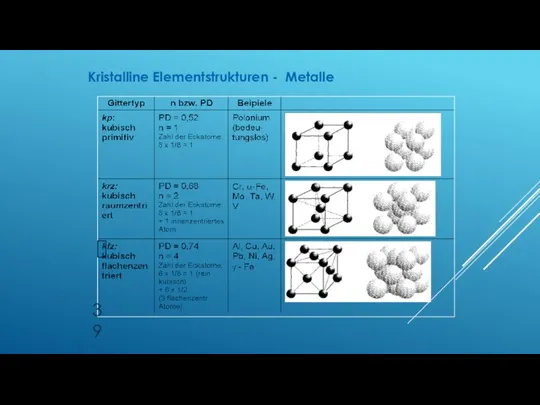
- 39. Kristalline Elementstrukturen - Metalle
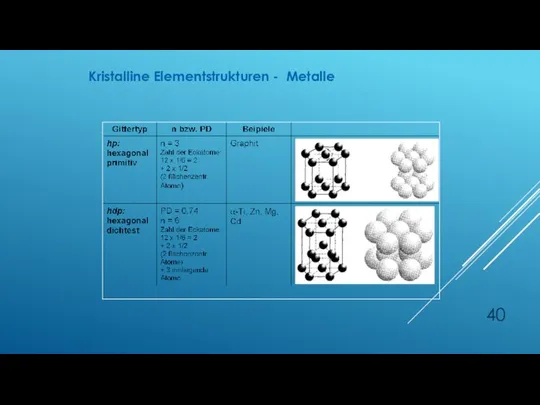
- 40. Kristalline Elementstrukturen - Metalle
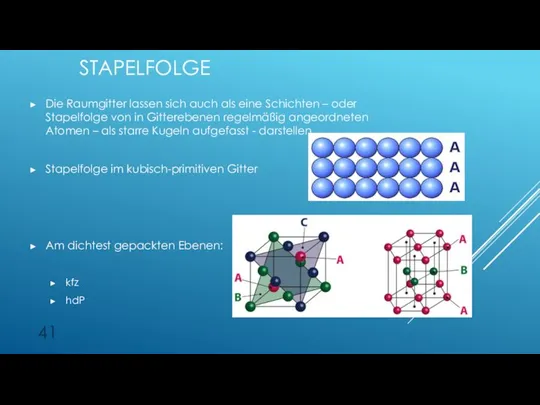
- 41. Die Raumgitter lassen sich auch als eine Schichten – oder Stapelfolge von in Gitterebenen regelmäßig angeordneten
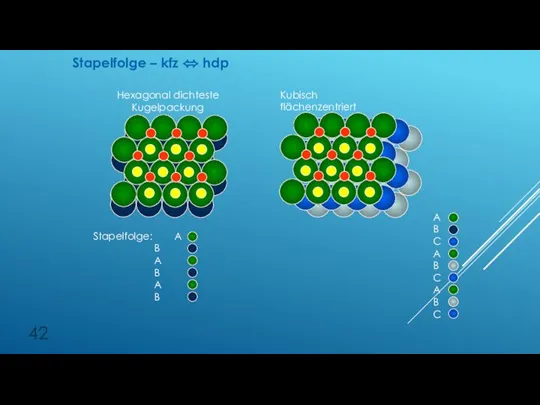
- 42. Hexagonal dichteste Kugelpackung Kubisch flächenzentriert Stapelfolge: A B A B A B A B C A
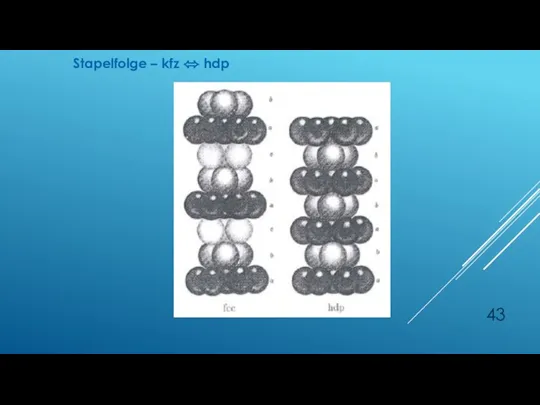
- 43. Stapelfolge – kfz ⬄ hdp
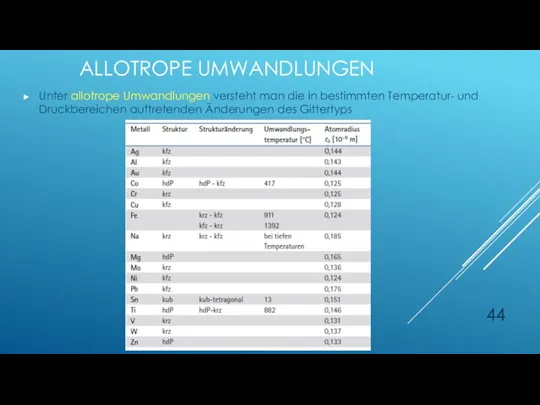
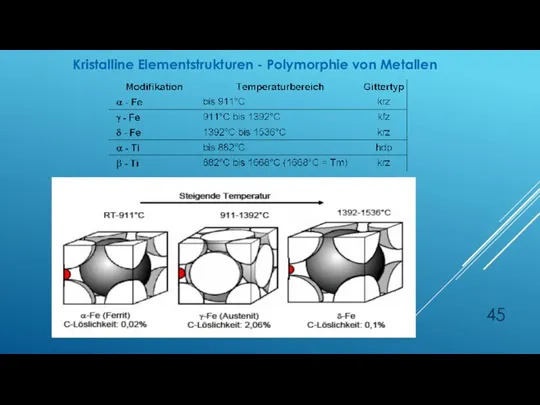
- 44. ALLOTROPE UMWANDLUNGEN Unter allotrope Umwandlungen versteht man die in bestimmten Temperatur- und Druckbereichen auftretenden Änderungen des
- 45. Kristalline Elementstrukturen - Polymorphie von Metallen
- 47. METALLE – KRISTALLZUSTAND DER METALLE - LERNZIELE Das Raumgitter als Idealstruktur bestimmt viele Eigenschaften und Vorgänge
- 48. BEZEICHNUNG VON PUNKTEN UND EBENEN IM RAUMGITTER (MILLERSCHE INDIZES)
- 49. BEZEICHNUNG VON PUNKTEN UND EBENEN IM RAUMGITTER (MILLERSCHE INDIZES) (hkl) wird als Millersche Indizes bezeichnet Definition
- 50. Beispiele
- 51. Beispiele
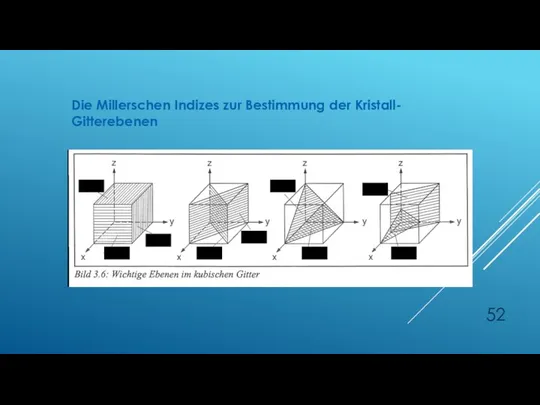
- 52. Die Millerschen Indizes zur Bestimmung der Kristall- Gitterebenen
- 53. Die Millerschen Indizes zur Bestimmung der Kristall- Gitterebenen
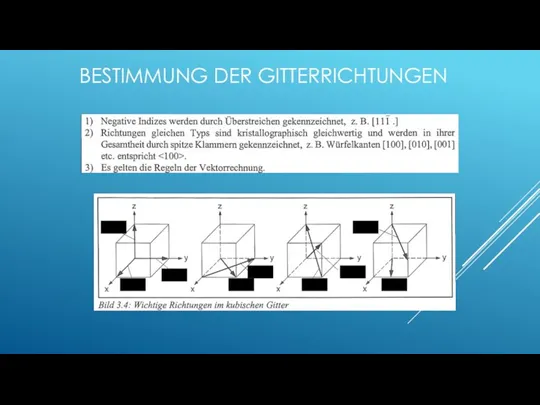
- 54. BESTIMMUNG DER GITTERRICHTUNGEN
- 55. BESTIMMUNG DER GITTERRICHTUNGEN
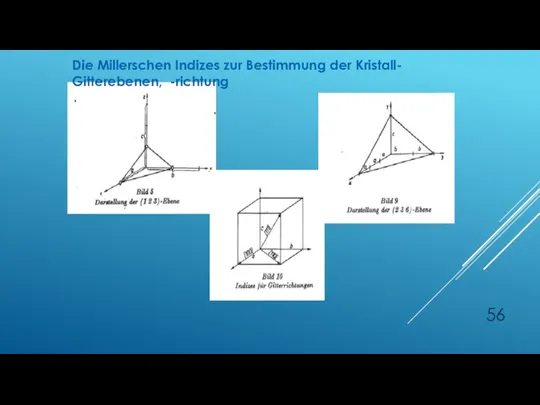
- 56. Die Millerschen Indizes zur Bestimmung der Kristall- Gitterebenen, -richtung
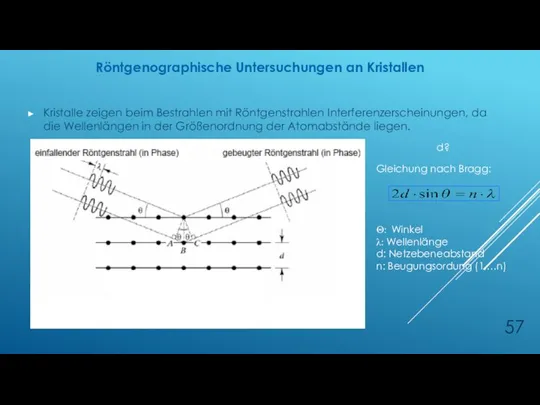
- 57. Röntgenographische Untersuchungen an Kristallen Kristalle zeigen beim Bestrahlen mit Röntgenstrahlen Interferenzerscheinungen, da die Wellenlängen in der
- 58. Röntgenographische Untersuchungen an Kristallen
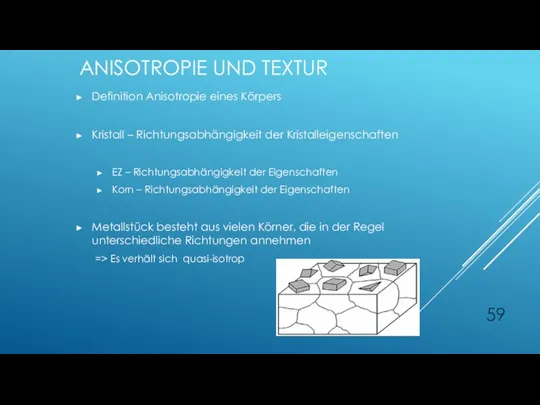
- 59. ANISOTROPIE UND TEXTUR Definition Anisotropie eines Körpers Kristall – Richtungsabhängigkeit der Kristalleigenschaften EZ – Richtungsabhängigkeit der
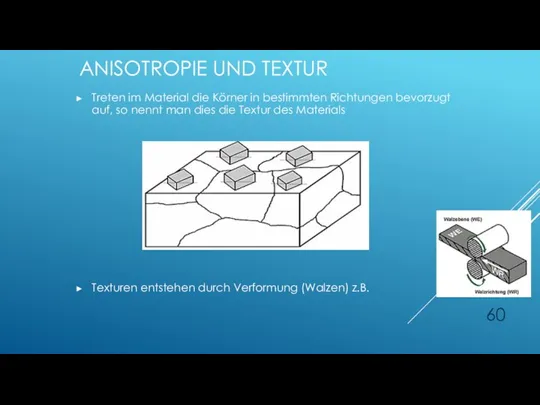
- 60. ANISOTROPIE UND TEXTUR Treten im Material die Körner in bestimmten Richtungen bevorzugt auf, so nennt man
- 61. REALSTRUKTUR: KRISTALLBAUFEHLER Im Gegensatz zu den Idealkristallen sind die existierenden Realkristalle mit Fehler behaftet. Man unterscheidet:
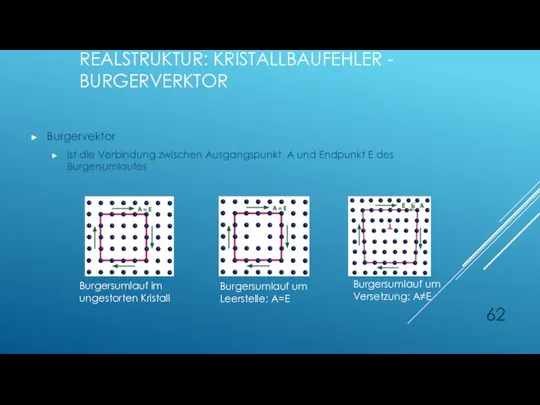
- 62. REALSTRUKTUR: KRISTALLBAUFEHLER - BURGERVERKTOR Burgervektor Ist die Verbindung zwischen Ausgangspunkt A und Endpunkt E des Burgersumlaufes
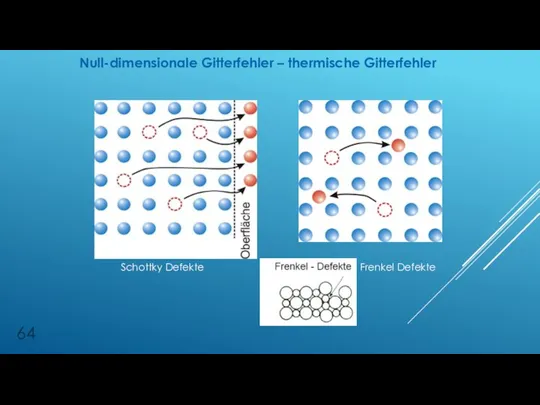
- 63. NULL-DIMENSIONALE GITTERFEHLER – THERMISCHE GITTERFEHLER Auch Gitterlücken oder Schottky Defekte genannt Die Entstehung einer Leerstelle kann
- 64. Null-dimensionale Gitterfehler – thermische Gitterfehler Schottky Defekte Frenkel Defekte
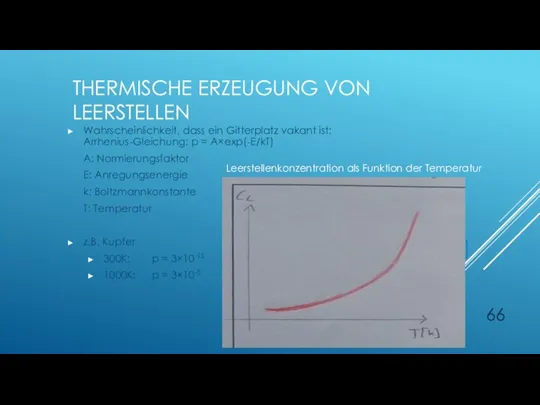
- 65. THERMISCHE ERZEUGUNG VON LEERSTELLEN Wahrscheinlichkeit, dass ein Gitterplatz vakant ist: Arrhenius-Gleichung: p = A×exp(-E/kT) A: Normierungsfaktor
- 66. THERMISCHE ERZEUGUNG VON LEERSTELLEN Wahrscheinlichkeit, dass ein Gitterplatz vakant ist: Arrhenius-Gleichung: p = A×exp(-E/kT) A: Normierungsfaktor
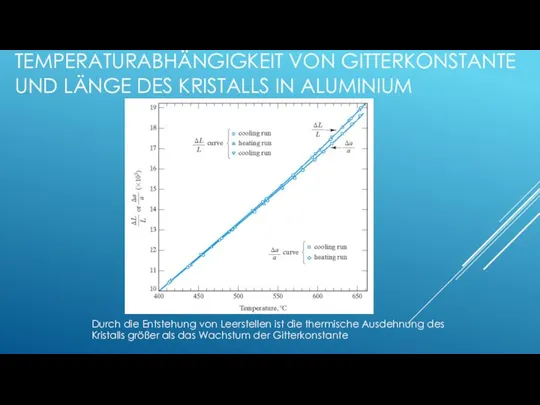
- 67. TEMPERATURABHÄNGIGKEIT VON GITTERKONSTANTE UND LÄNGE DES KRISTALLS IN ALUMINIUM Durch die Entstehung von Leerstellen ist die
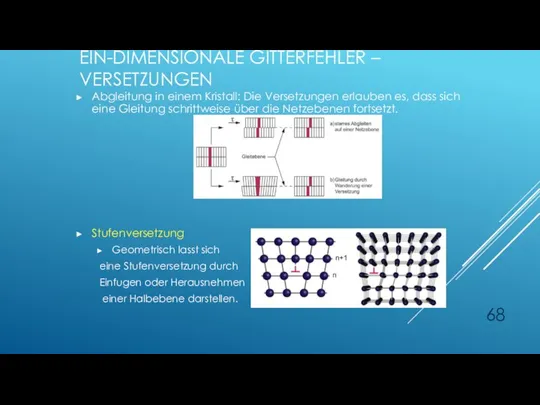
- 68. EIN-DIMENSIONALE GITTERFEHLER – VERSETZUNGEN Abgleitung in einem Kristall: Die Versetzungen erlauben es, dass sich eine Gleitung
- 69. Stufenversetzung 1-dimensionaler Fehler Burgervektor senkrecht zur Versetzung
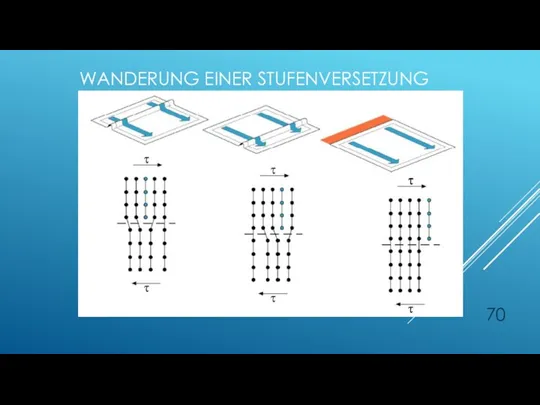
- 70. WANDERUNG EINER STUFENVERSETZUNG
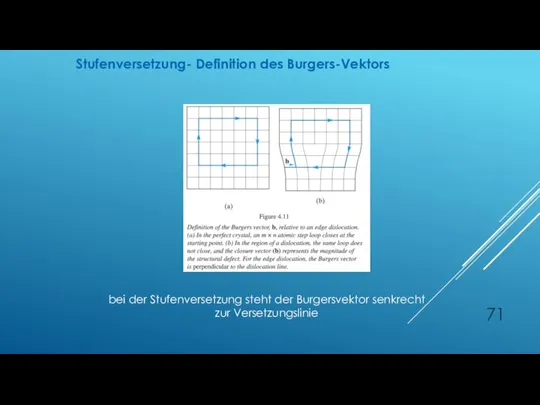
- 71. Stufenversetzung- Definition des Burgers-Vektors bei der Stufenversetzung steht der Burgersvektor senkrecht zur Versetzungslinie
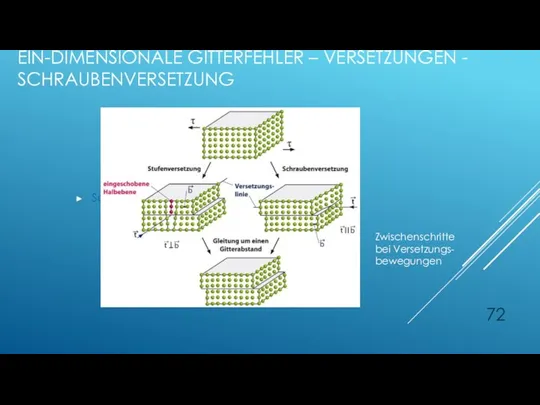
- 72. EIN-DIMENSIONALE GITTERFEHLER – VERSETZUNGEN - SCHRAUBENVERSETZUNG Schraubenversetzung Zwischenschritte bei Versetzungs- bewegungen
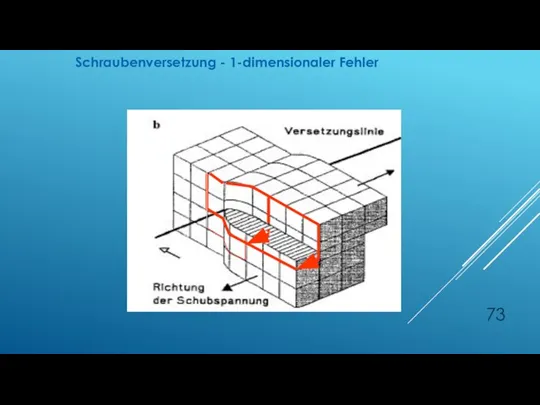
- 73. Schraubenversetzung - 1-dimensionaler Fehler
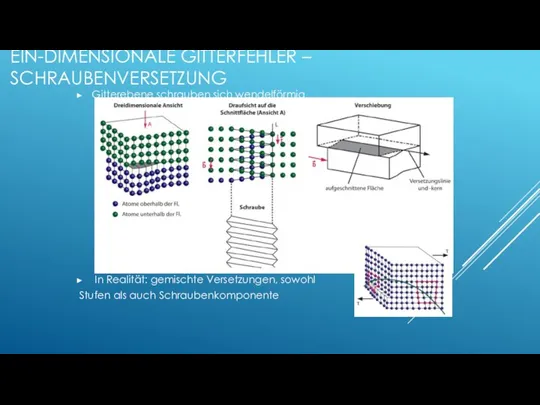
- 74. EIN-DIMENSIONALE GITTERFEHLER – SCHRAUBENVERSETZUNG Gitterebene schrauben sich wendelförmig In Realität: gemischte Versetzungen, sowohl Stufen als auch
- 75. EIN-DIMENSIONALE GITTERFEHLER Ursprung von Versetzungen Zufällige Missorientierung beim Wachstum von Kristallen Ausscheiden von überschüssigen Leerstellen Abbau
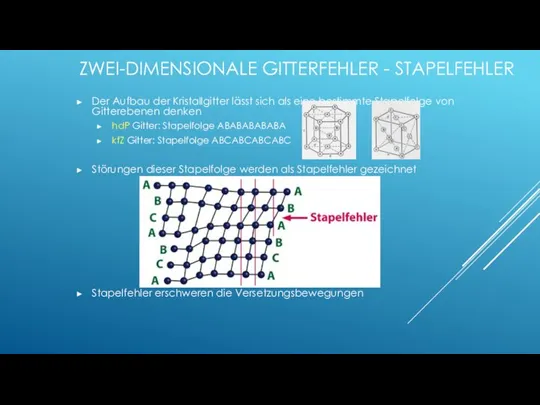
- 76. ZWEI-DIMENSIONALE GITTERFEHLER - STAPELFEHLER Der Aufbau der Kristallgitter lässt sich als eine bestimmte Stapelfolge von Gitterebenen
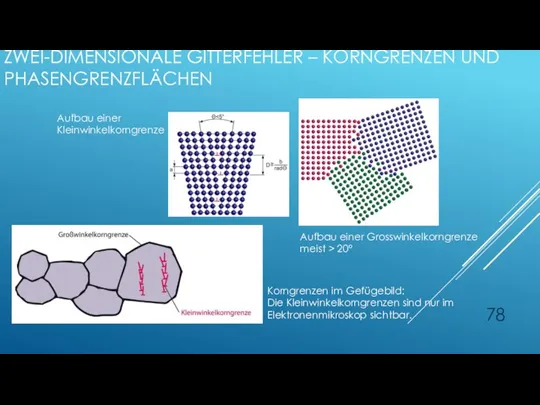
- 77. ZWEI-DIMENSIONALE GITTERFEHLER – KORNGRENZEN UND PHASENGRENZFLÄCHEN Unter Korngrenze im engeren Sinn versteht man die Grenzfläche zwischen
- 78. ZWEI-DIMENSIONALE GITTERFEHLER – KORNGRENZEN UND PHASENGRENZFLÄCHEN Aufbau einer Kleinwinkelkorngrenze Aufbau einer Grosswinkelkorngrenze meist > 20° Korngrenzen
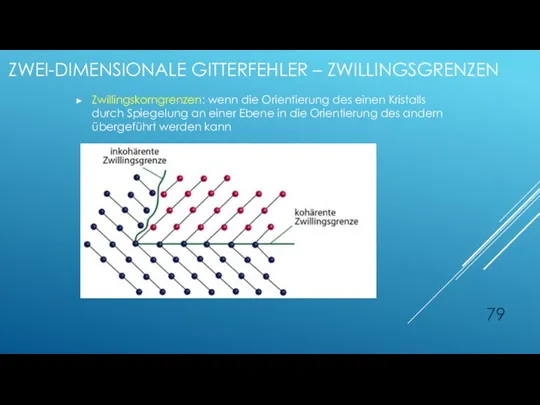
- 79. ZWEI-DIMENSIONALE GITTERFEHLER – ZWILLINGSGRENZEN Zwillingskorngrenzen: wenn die Orientierung des einen Kristalls durch Spiegelung an einer Ebene
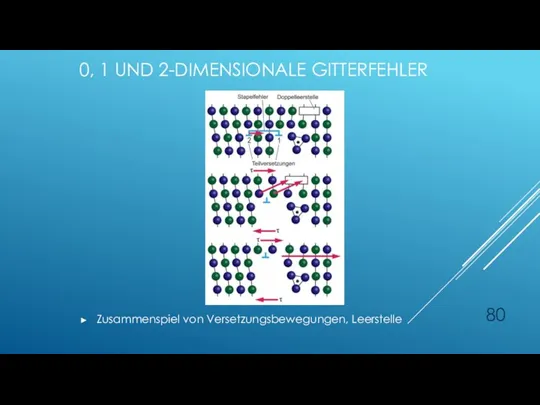
- 80. 0, 1 UND 2-DIMENSIONALE GITTERFEHLER Zusammenspiel von Versetzungsbewegungen, Leerstelle
- 81. METALLE – KRISTALLZUSTAND DER METALLE - LERNZIELE Das Raumgitter als Idealstruktur bestimmt viele Eigenschaften und Vorgänge
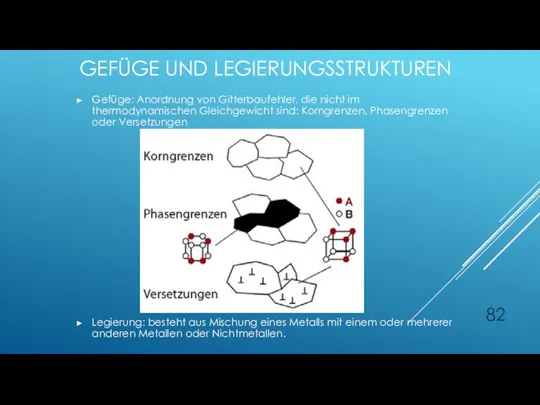
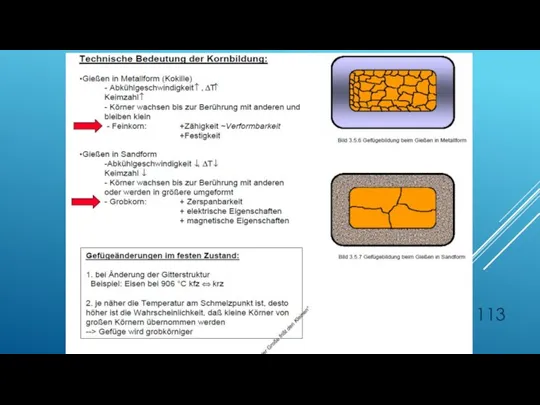
- 82. GEFÜGE UND LEGIERUNGSSTRUKTUREN Gefüge: Anordnung von Gitterbaufehler, die nicht im thermodynamischen Gleichgewicht sind: Korngrenzen, Phasengrenzen oder
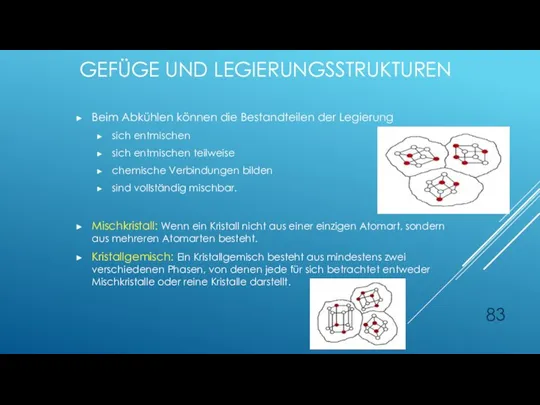
- 83. Beim Abkühlen können die Bestandteilen der Legierung sich entmischen sich entmischen teilweise chemische Verbindungen bilden sind
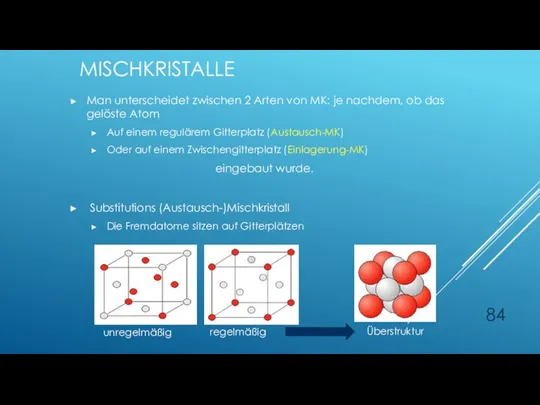
- 84. MISCHKRISTALLE Man unterscheidet zwischen 2 Arten von MK: je nachdem, ob das gelöste Atom Auf einem
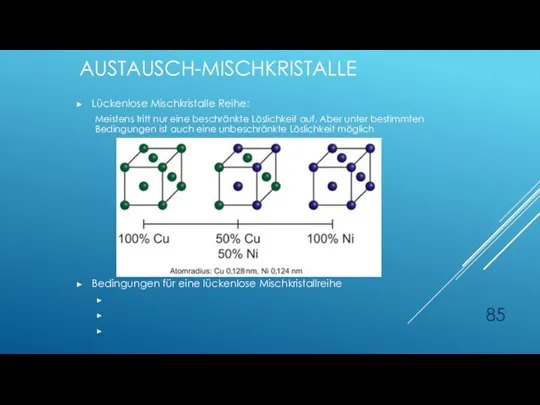
- 85. AUSTAUSCH-MISCHKRISTALLE Lückenlose Mischkristalle Reihe: Meistens tritt nur eine beschränkte Löslichkeit auf. Aber unter bestimmten Bedingungen ist
- 86. EINLAGERUNGS-MISCHKRISTALL Die Fremdatome sitzen auf Zwischengitterplätzen Bedingung: Sind Legierungsatome (Radius r1) im Verhältnis zum Atomradius r2
- 87. Allgemeines: Die physikalische und technische Eigenschaften sind sowohl vom Grundgitter Art, Anzahl der Anordnung der Gitterfehler
- 88. DIFFUSION – ENERGETISCHE BETRACHTUNG Diffusion eines (Fremd)atoms bzw. einer Leerstelle Diffusion erfordert die Überwindung einer Energiebarriere
- 89. DIFFUSION – BEWEGUNG IM GITTER Diffusion die thermische Anregung bestimmt die Häufigkeit der Diffusionsschritte die Richtung
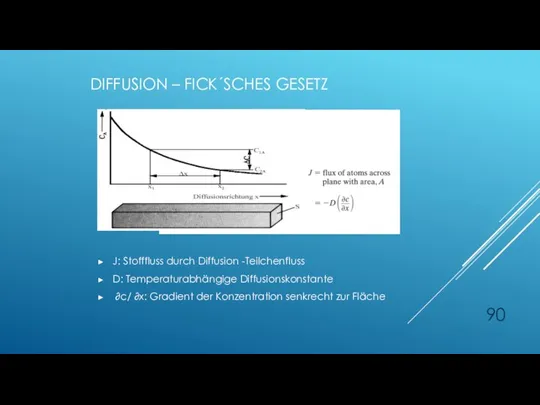
- 90. DIFFUSION – FICK´SCHES GESETZ J: Stofffluss durch Diffusion -Teilchenfluss D: Temperaturabhängige Diffusionskonstante ∂c/ ∂x: Gradient der
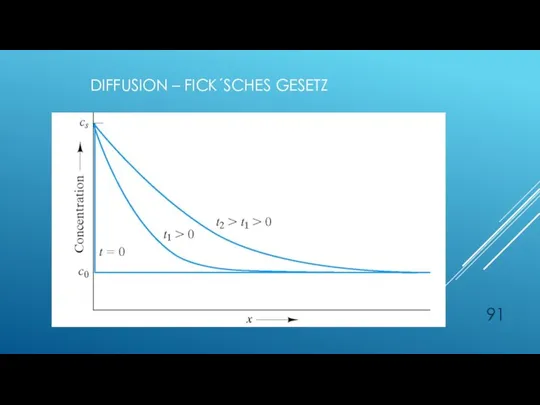
- 91. DIFFUSION – FICK´SCHES GESETZ
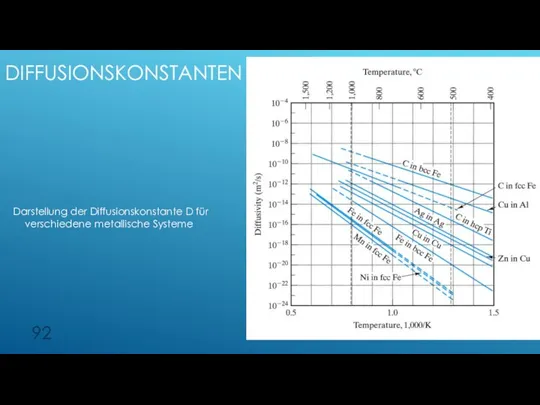
- 92. DIFFUSIONSKONSTANTEN Darstellung der Diffusionskonstante D für verschiedene metallische Systeme
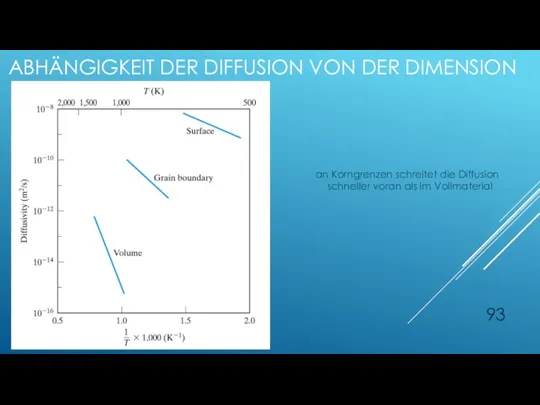
- 93. ABHÄNGIGKEIT DER DIFFUSION VON DER DIMENSION an Korngrenzen schreitet die Diffusion schneller voran als im Vollmaterial
- 94. Fliesseigenschaften des Kristalls plastische Verformbarkeit der Metall ⬄ Versetzungen in bevorzugten Gleitebenen ermöglicht! Gleitebenen und Gleitrichtungen
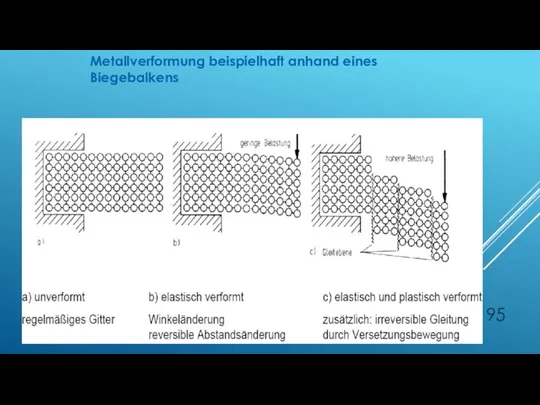
- 95. Metallverformung beispielhaft anhand eines Biegebalkens
- 96. Gleitebenen von Metallen
- 98. Übungen: Einfluss auf der mechansiche Eigenschaften 2 Zugstäbchen: 1 Alu (kfz) und 1 Mg (hex.) Frage:
- 99. Übungen: Einfluss auf der mech. Eigenschaften
- 100. INHALT Legierung Abkühlungskurve Zustandsdiagramm vollständige Löslichkeit im flüssigen und festen Zustand vollständige Löslichkeit im flüssigen und
- 101. Legierungskunde – Zustandsdiagramme - Lernziel Bestimmung des Komponentengehalts der Phasen in Zweistoffsystemen mit Ein-, Zwei- und
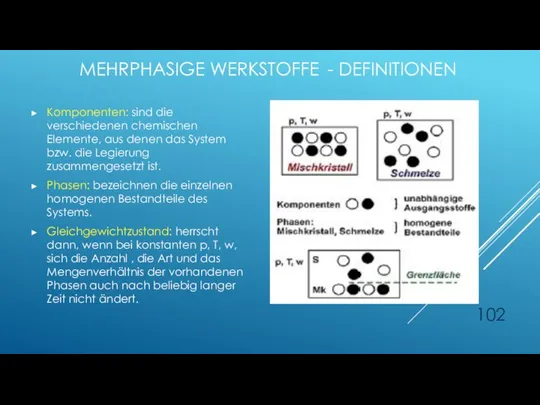
- 102. MEHRPHASIGE WERKSTOFFE - DEFINITIONEN Komponenten: sind die verschiedenen chemischen Elemente, aus denen das System bzw. die
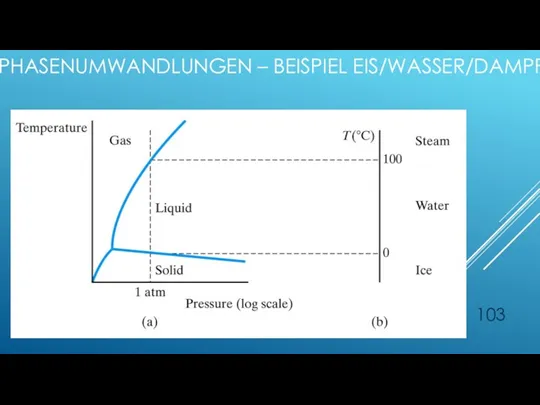
- 103. PHASENUMWANDLUNGEN – BEISPIEL EIS/WASSER/DAMPF
- 104. GRUNDLAGEN -THERMODYNAMIK Enthalpie: Wärmeinhalt eines stofflichen Systems bei konstantem Druck. Hs: Wärmeinhalt zum Erstarren (Schmelzen) Hv:
- 105. ENERGIE EINES WERKSTOFFSYSTEMS Gesamtenergieinhalt E eines Systems E= Epot + Ekin + Ech + Eth Im
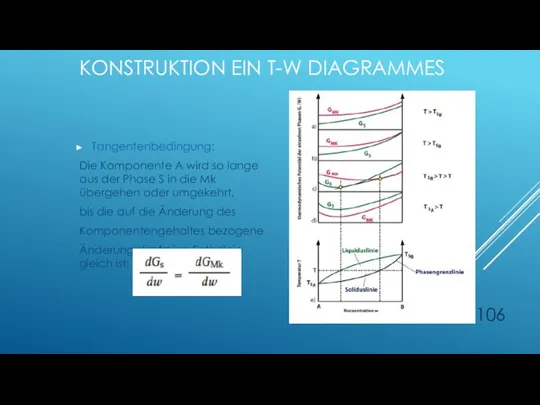
- 106. Tangentenbedingung: Die Komponente A wird so lange aus der Phase S in die Mk übergehen oder
- 107. BINÄRES ZUSTANDSDIAGRAMM In metallischen Systemen werden die Verhältnisse in Abhängigkeit von Gehalt und Temperatur sogenannte „Gehalts-Temperaturschaubilder“
- 108. Reine Stoffe: A, B Mischkristall: α, β, γ, ε Schmelze: S Komponentengehalt der Phasen: wΑα, WΑs
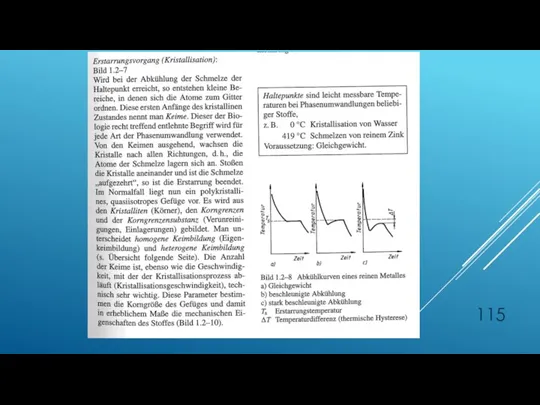
- 109. AUFSTELLEN VON ZUSTANDSDIAGRAMMEN Ziel: Ermitteln der Phasengrenzlinien im T-w Schaubild Beim Abkühlen: Haltepunkt (1): die Temperatur
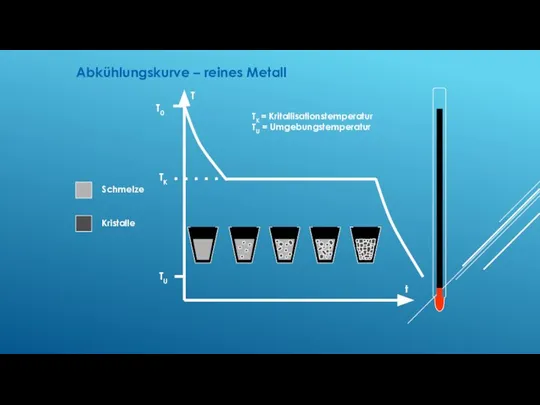
- 110. t T T0 TK = Kritallisationstemperatur TU = Umgebungstemperatur Schmelze Kristalle TK TU Abkühlungskurve – reines
- 111. ABKÜHLUNGSKURVE
- 114. Wie sehen die Abkühlkurven eines reinen Materialles Gleichgewicht Beschleunigte Abkühlung Stark beschleunigte Abkühlung? Einfluss der Keimzahl
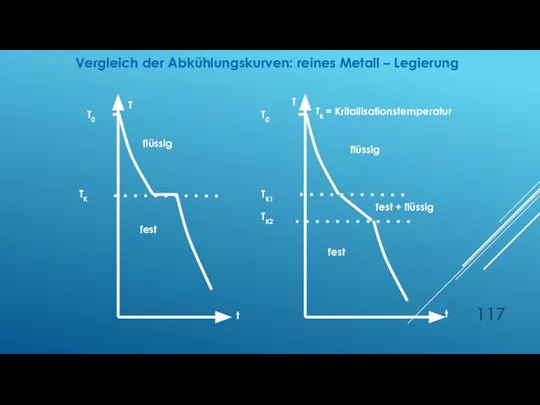
- 117. TK = Kritallisationstemperatur t T T0 TK T T0 TK1 TK2 t flüssig fest fest +
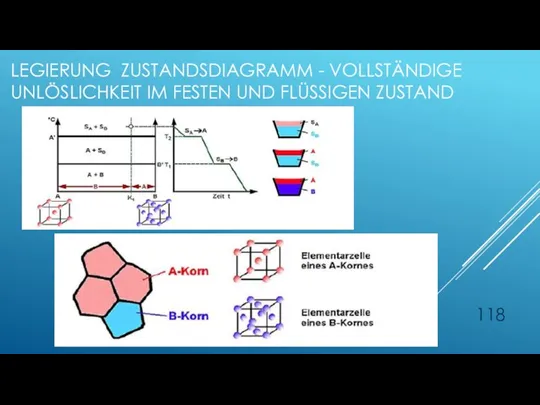
- 118. LEGIERUNG ZUSTANDSDIAGRAMM - VOLLSTÄNDIGE UNLÖSLICHKEIT IM FESTEN UND FLÜSSIGEN ZUSTAND
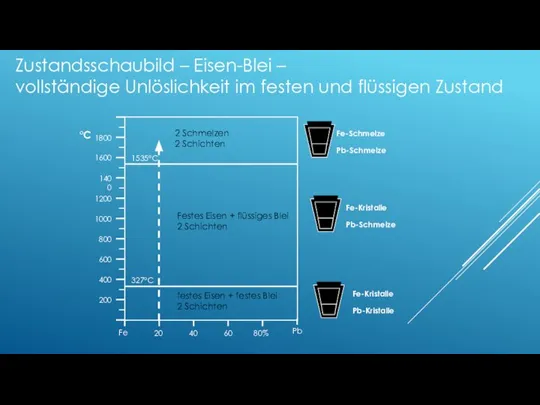
- 119. Fe-Schmelze Pb-Schmelze Fe-Kristalle Pb-Schmelze Fe-Kristalle Pb-Kristalle Zustandsschaubild – Eisen-Blei – vollständige Unlöslichkeit im festen und flüssigen
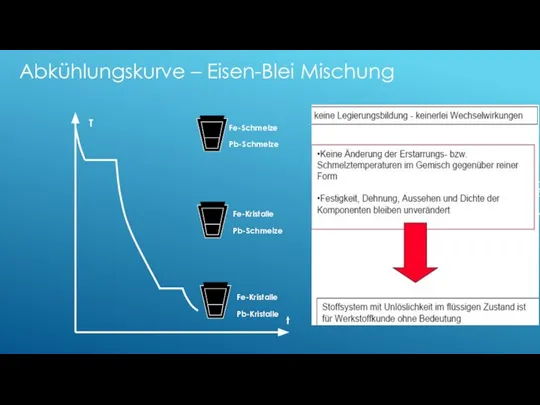
- 120. Fe-Schmelze Pb-Schmelze Fe-Kristalle Pb-Schmelze Fe-Kristalle Pb-Kristalle t T Abkühlungskurve – Eisen-Blei Mischung
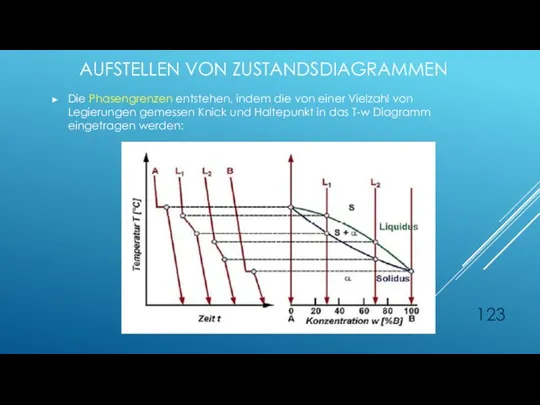
- 123. AUFSTELLEN VON ZUSTANDSDIAGRAMMEN Die Phasengrenzen entstehen, indem die von einer Vielzahl von Legierungen gemessen Knick und
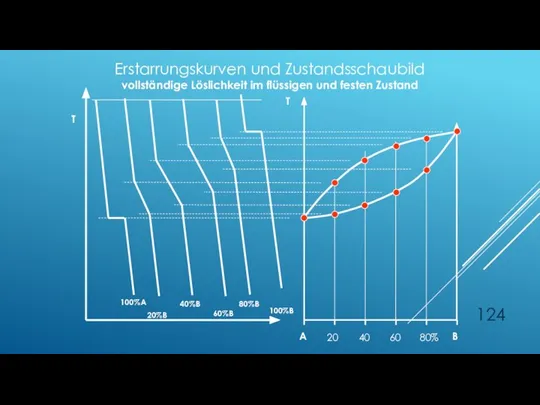
- 124. T A B 20 40 60 80% 100%A 20%B 40%B 60%B 80%B 100%B T Erstarrungskurven und
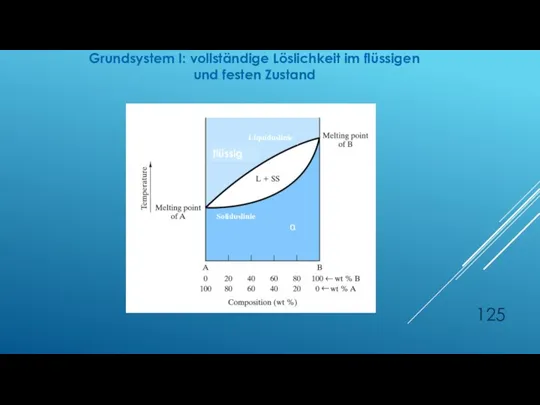
- 125. α flüssig Liquiduslinie Soliduslinie Grundsystem I: vollständige Löslichkeit im flüssigen und festen Zustand
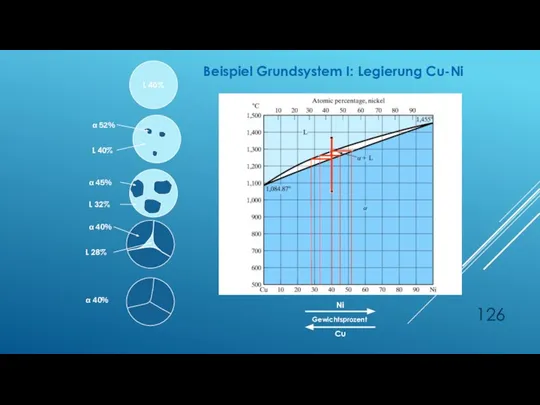
- 126. Gewichtsprozent Ni Cu L 40% Beispiel Grundsystem I: Legierung Cu-Ni
- 127. Das Hebel Gesetz Ziel: Ermittlung der Massenanteile der beiden Phasen mit Hilfe des Hebelgesetztes
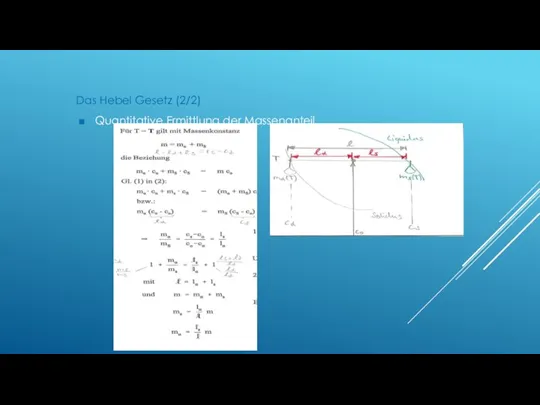
- 128. Das Hebel Gesetz (2/2) Quantitative Ermittlung der Massenanteil
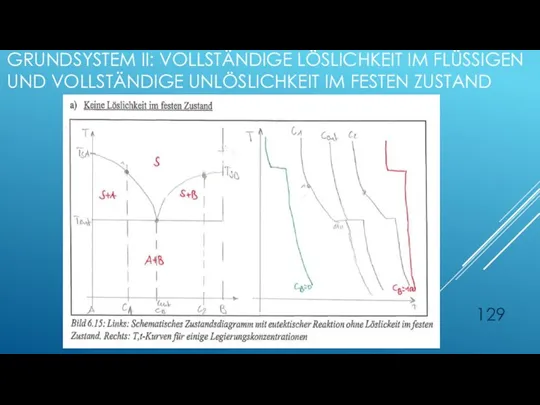
- 129. GRUNDSYSTEM II: VOLLSTÄNDIGE LÖSLICHKEIT IM FLÜSSIGEN UND VOLLSTÄNDIGE UNLÖSLICHKEIT IM FESTEN ZUSTAND
- 130. Alles flüssig Kristallite von B in L Kristallite von A in L L eutektisch Eutektische Mikrostruktur
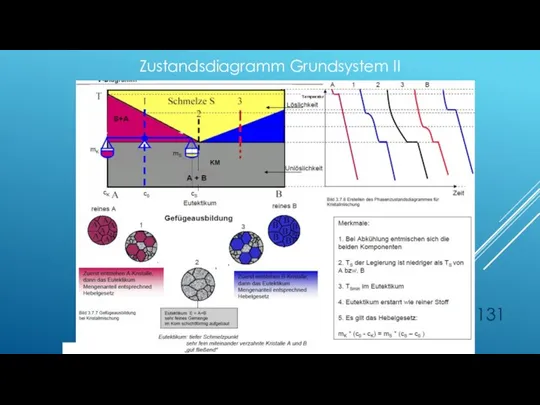
- 131. Zustandsdiagramm Grundsystem II
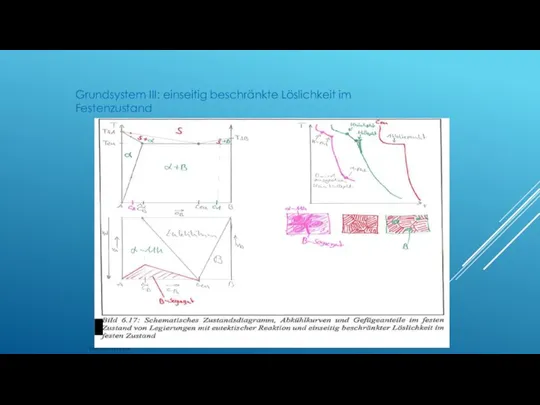
- 132. Grundsystem III: einseitig beschränkte Löslichkeit im Festenzustand Werkstoffkunde
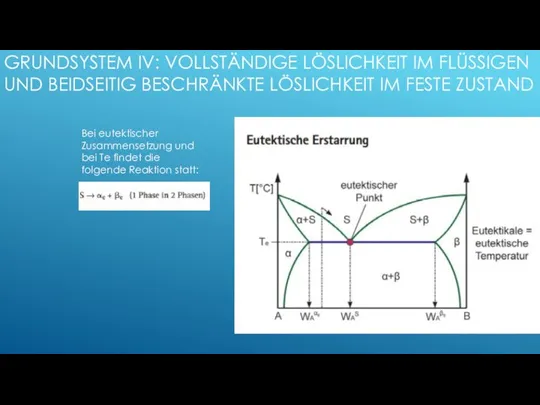
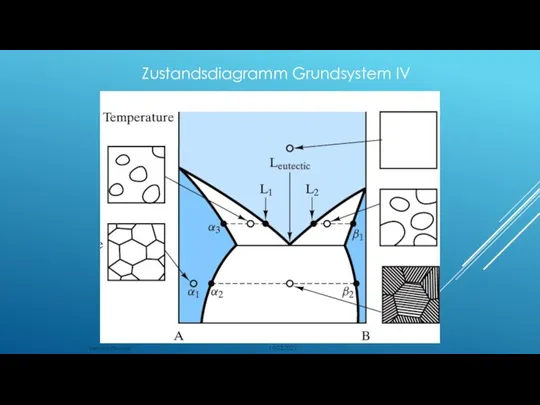
- 133. GRUNDSYSTEM IV: VOLLSTÄNDIGE LÖSLICHKEIT IM FLÜSSIGEN UND BEIDSEITIG BESCHRÄNKTE LÖSLICHKEIT IM FESTE ZUSTAND Bei eutektischer Zusammensetzung
- 134. GRUNDSYSTEM IV: VOLLSTÄNDIGE LÖSLICHKEIT IM FLÜSSIGEN UND BEIDSEITIG BESCHRÄNKTE LÖSLICHKEIT IM FESTE ZUSTAND
- 135. Zustandsdiagramm Grundsystem IV 18.02.2021 Werkstoffkunde
- 136. HEBELGESETZ - GRUNDSYSTEM III
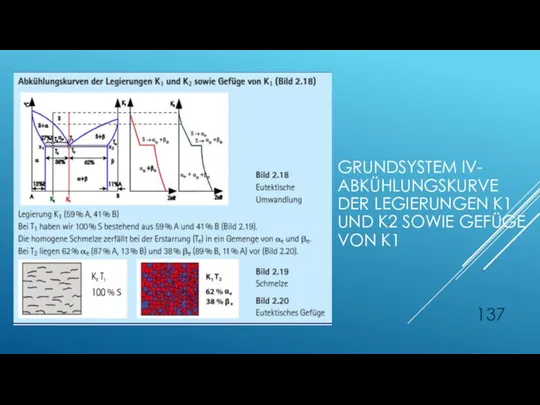
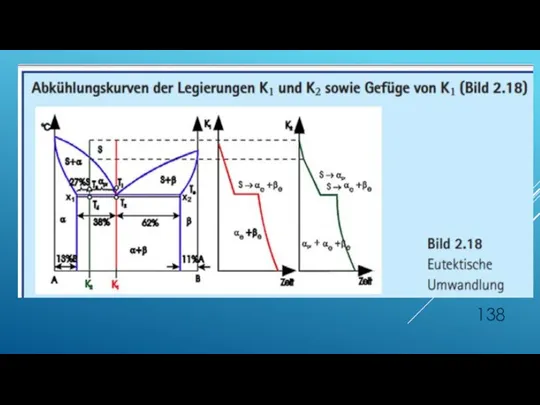
- 137. GRUNDSYSTEM IV- ABKÜHLUNGSKURVE DER LEGIERUNGEN K1 UND K2 SOWIE GEFÜGE VON K1
- 139. GRUNDSYSTEM IV-PHASENREAKTION UND GEFÜGE DER ERSTARRUNG DER LEGIERUNG K2
- 140. GRUNDSYSTEM V - PERITEKTISCHE ERSTARRUNG Wenn die Schmelztemperaturen der Komponenten sehr verschieden hoch sind, liegt meist
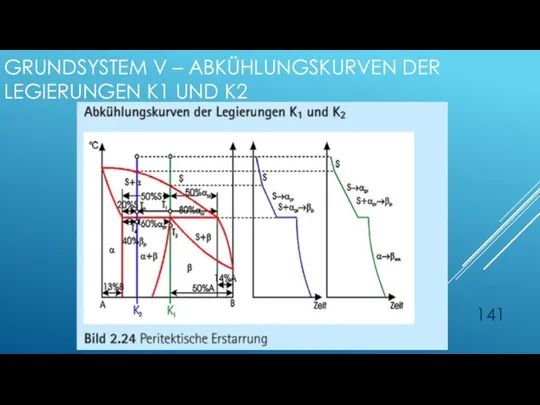
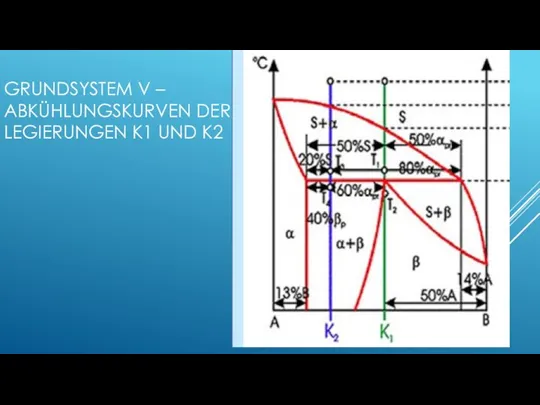
- 141. GRUNDSYSTEM V – ABKÜHLUNGSKURVEN DER LEGIERUNGEN K1 UND K2
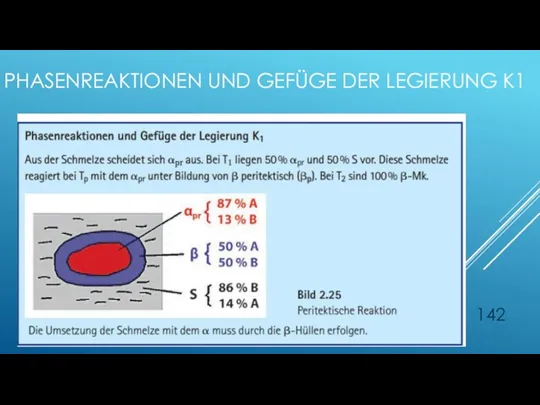
- 142. PHASENREAKTIONEN UND GEFÜGE DER LEGIERUNG K1
- 143. GRUNDSYSTEM V – ABKÜHLUNGSKURVEN DER LEGIERUNGEN K1 UND K2
- 144. PHASENREAKTIONEN UND GEFÜGE DER LEGIERUNG K2
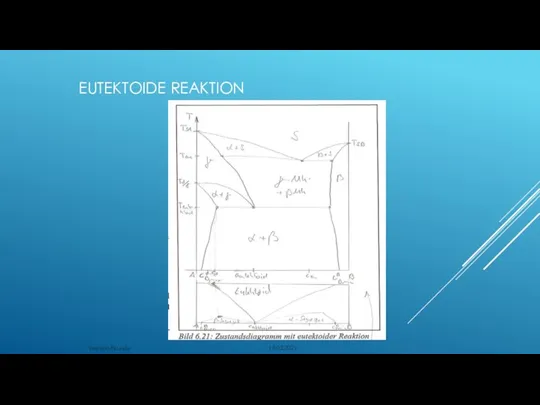
- 145. Umwandlungen in festen Zustand Eutektoide Reaktion Analogie zur eutektischen Reaktionen Statt Zerfall der Schmelze in 2
- 146. EUTEKTOIDE REAKTION Werkstoffkunde 18.02.2021
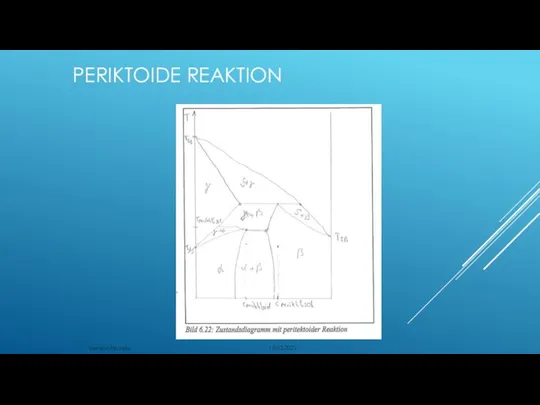
- 147. PERIKTOIDE REAKTION Werkstoffkunde 18.02.2021
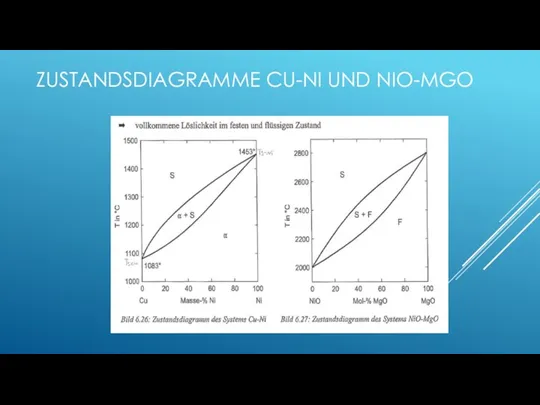
- 148. ZUSTANDSDIAGRAMME CU-NI UND NIO-MGO
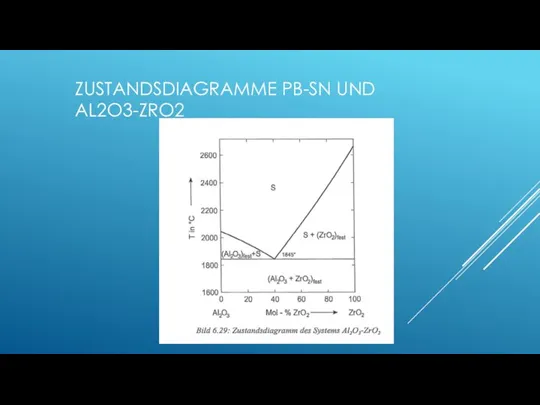
- 149. ZUSTANDSDIAGRAMME PB-SN UND AL2O3-ZRO2
- 150. ZUSTANDSDIAGRAMME PB-SN UND AL2O3-ZRO2
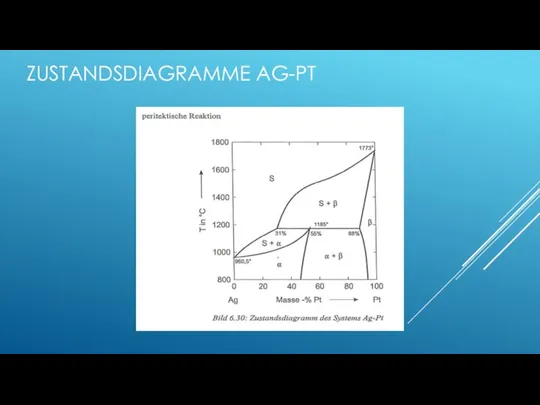
- 151. ZUSTANDSDIAGRAMME AG-PT
- 152. ÜBUNGEN
- 153. REALES ZUSTANDSDIAGRAMM: FE-FE3C Eisen Das Eisen ist das 26.Element im Periodensystem der Elemente Es gehört zu
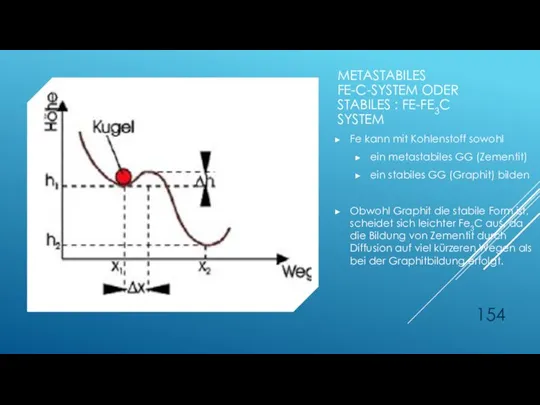
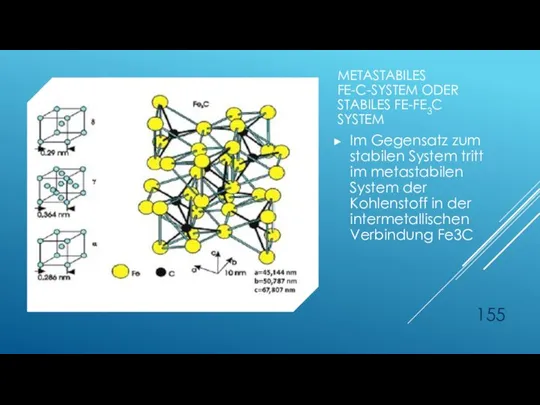
- 154. METASTABILES FE-C-SYSTEM ODER STABILES : FE-FE3C SYSTEM Fe kann mit Kohlenstoff sowohl ein metastabiles GG (Zementit)
- 155. METASTABILES FE-C-SYSTEM ODER STABILES FE-FE3C SYSTEM Im Gegensatz zum stabilen System tritt im metastabilen System der
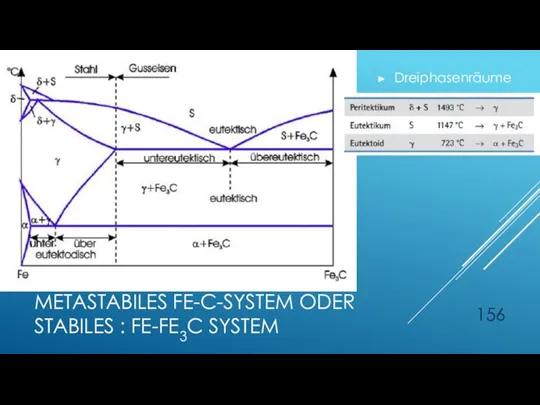
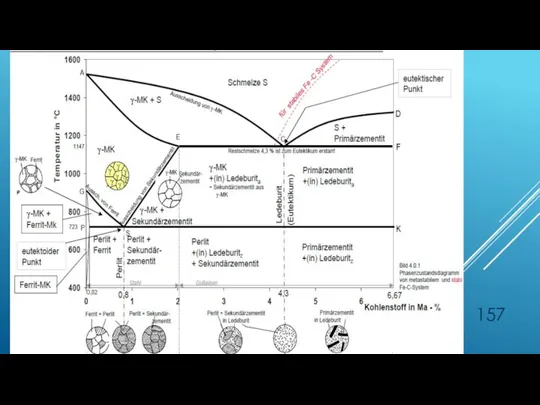
- 156. Dreiphasenräume METASTABILES FE-C-SYSTEM ODER STABILES : FE-FE3C SYSTEM
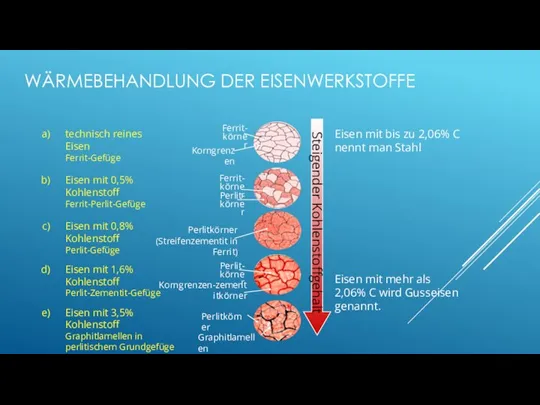
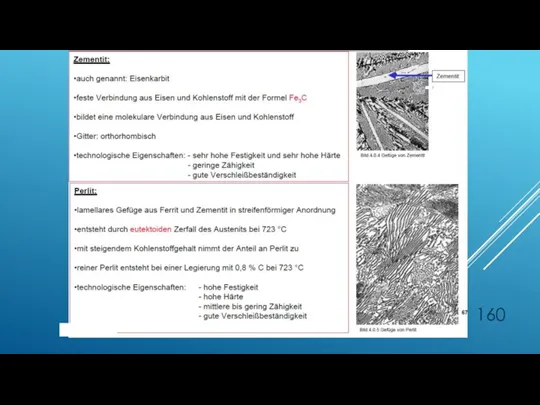
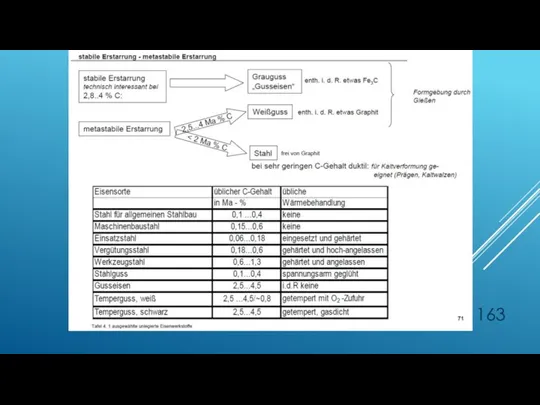
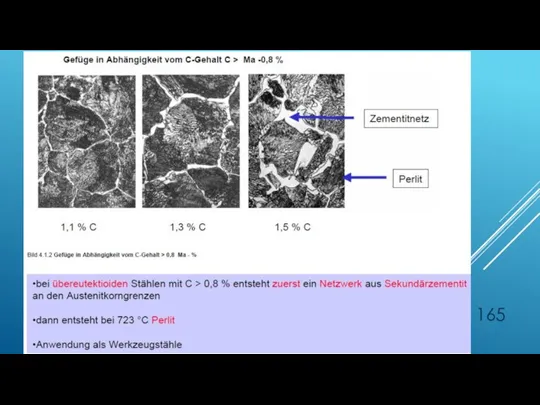
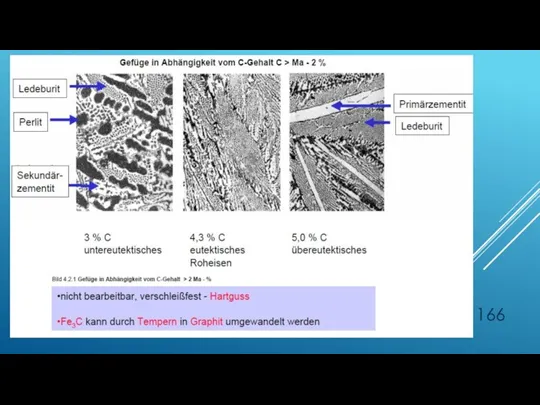
- 158. WÄRMEBEHANDLUNG DER EISENWERKSTOFFE Eisen mit bis zu 2,06% C nennt man Stahl Eisen mit mehr als
- 168. Скачать презентацию




































































 Презентация на тему Никола Тесла (1856-1943)
Презентация на тему Никола Тесла (1856-1943)  Ультразвуковые технологии. Технология 9 класс
Ультразвуковые технологии. Технология 9 класс Презентация (1)
Презентация (1) Электроемкость. Электроемкость конденсатора. Энергия конденсатора
Электроемкость. Электроемкость конденсатора. Энергия конденсатора Формирование исследовательских умений у учащихся 8 класса на уроках физики
Формирование исследовательских умений у учащихся 8 класса на уроках физики Работа. Мощность. Энергия
Работа. Мощность. Энергия Презентация на тему Теория относительности
Презентация на тему Теория относительности  Компьютерный расчёт геометрии механизма шагающего колеса
Компьютерный расчёт геометрии механизма шагающего колеса Интегральная и дифференциальная форма законов электродинамики. Лекция 2
Интегральная и дифференциальная форма законов электродинамики. Лекция 2 Гидравлические машины
Гидравлические машины Тепловые двигатели. Термодинамические циклы. Цикл Карно ГОУ СОШ № 625 Н.М.Турлакова
Тепловые двигатели. Термодинамические циклы. Цикл Карно ГОУ СОШ № 625 Н.М.Турлакова Физические свойства жидкостей
Физические свойства жидкостей Эффект Кайе Kaye effect
Эффект Кайе Kaye effect Гироскоп
Гироскоп Двигатели
Двигатели УСТРОЙСТВО Л.Л
УСТРОЙСТВО Л.Л Режимы течения жидкостей
Режимы течения жидкостей Теория относительности. (Лекция 4)
Теория относительности. (Лекция 4) Электромагнитная индукция
Электромагнитная индукция Отчёт по педагогической практике. Страны и континенты. Разные страны. Промыслы, культура
Отчёт по педагогической практике. Страны и континенты. Разные страны. Промыслы, культура Типовой расчет №3. Молекулярная физика и термодинамика
Типовой расчет №3. Молекулярная физика и термодинамика Тест. Вес тела. Связь между массой тела и силой тяжести
Тест. Вес тела. Связь между массой тела и силой тяжести Ультрафиолетовое излучение
Ультрафиолетовое излучение Единицы измерения скорости. Формула скорости
Единицы измерения скорости. Формула скорости Введение. Тест
Введение. Тест Основы химической кинетики
Основы химической кинетики Дифференцирующие и интегрирующие цепи
Дифференцирующие и интегрирующие цепи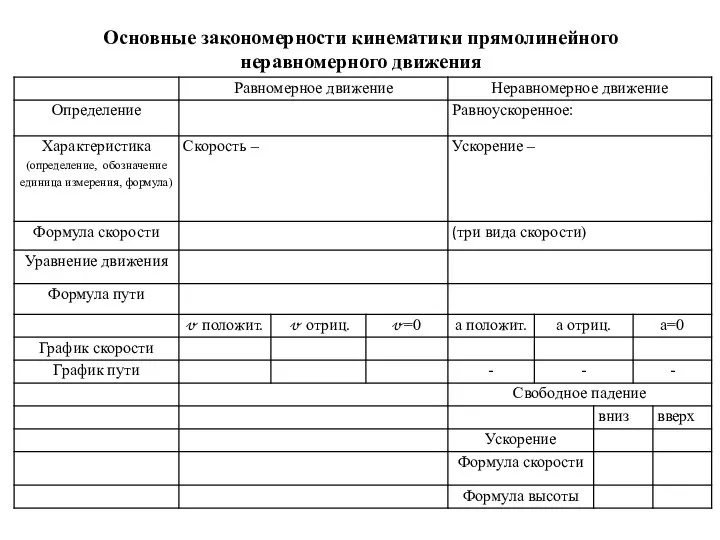 Закономерности кинематики прямолинейного неравномерного движения. Таблица
Закономерности кинематики прямолинейного неравномерного движения. Таблица