Слайд 2План занятия
Знакомство с понятием центра тяжести;
Методы нахождения центра тяжести;
Нахождение центра тяжести и

площадей простых геометрических фигур;
Нахождение центра тяжести стандартных прокатных профилей;
Нахождение центра тяжести объемных фигур
Слайд 3Центром тяжести называется центр параллельных сил тяжести всех элементарных частиц, из которых

состоит тело.
Слайд 4Методы нахождения центра тяжести
Метод симметрии
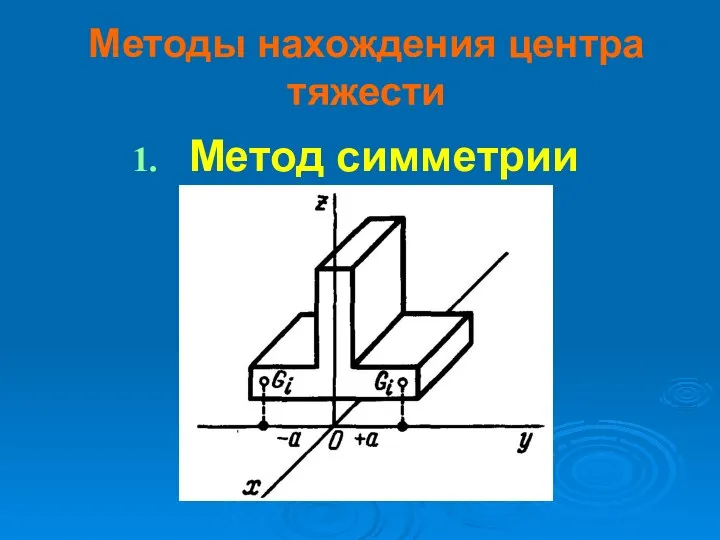
Слайд 5Если однородное тело имеет площадь симметрии, то центр тяжести лежит в этой

плоскости.
Слайд 6 если однородное тело имеет ось симметрии, то центр тяжести тела лежит

на этой оси;
если однородное тело имеет 2 оси симметрии, то центр тяжести тела находится в точке их пересечения;
центр тяжести однородного тела вращения лежит на оси вращения.
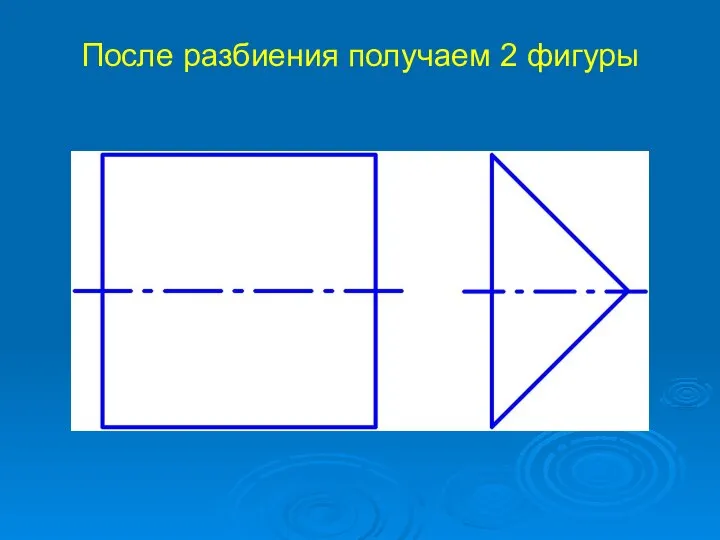
Слайд 8После разбиения получаем 2 фигуры
Слайд 9Где А1- площадь первой фигуры;
А2- площадь второй фигуры;
Аn- площадь n-ой

фигуры;
Х1- координата х центра тяжести первой фигуры;
Х2- координата х центра тяжести второй фигуры;
Х3- координата х центра тяжести n-ой фигуры;
n – число частей, на которое разбито тело.
Слайд 10Где А1- площадь первой фигуры;
А2- площадь второй фигуры;
Аn- площадь n-ой

фигуры;
y1- координата y центра тяжести первой фигуры;
y2- координата y центра тяжести второй фигуры;
y3- координата y центра тяжести n-ой фигуры;
n – число частей, на которое разбито тело.
Слайд 12
Где А1- площадь первой фигуры;
А2- площадь второй фигуры;
Х1- координата х центра

тяжести первой фигуры;
Х2- координата х центра тяжести второй фигуры;
Слайд 13
Где А1- площадь первой фигуры;
А2- площадь второй фигуры;
у1- координата у центра

тяжести первой фигуры;
у2- координата у центра тяжести второй фигуры;
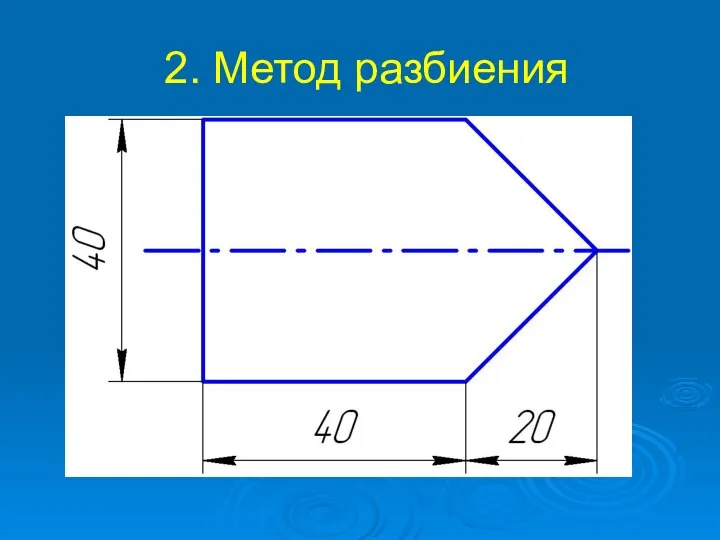
Слайд 143. Нахождение центра тяжести и площадей геометрических фигур, на которые может быть

разделено тело.
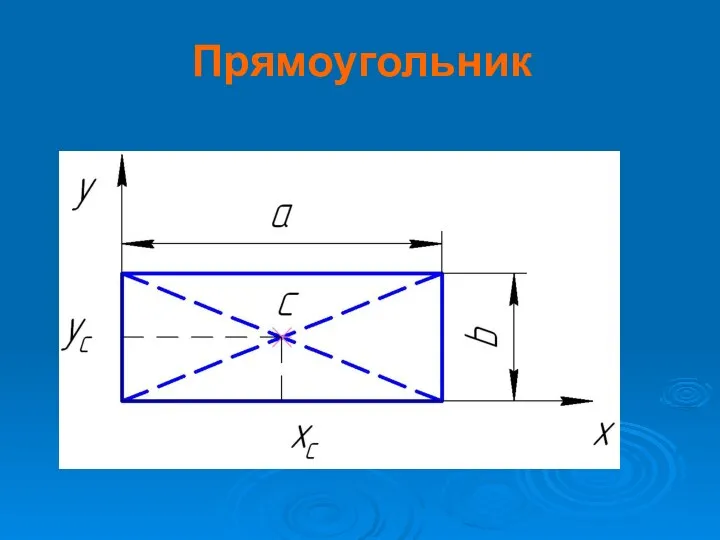
Слайд 16
Где а и b– стороны прямоугольника

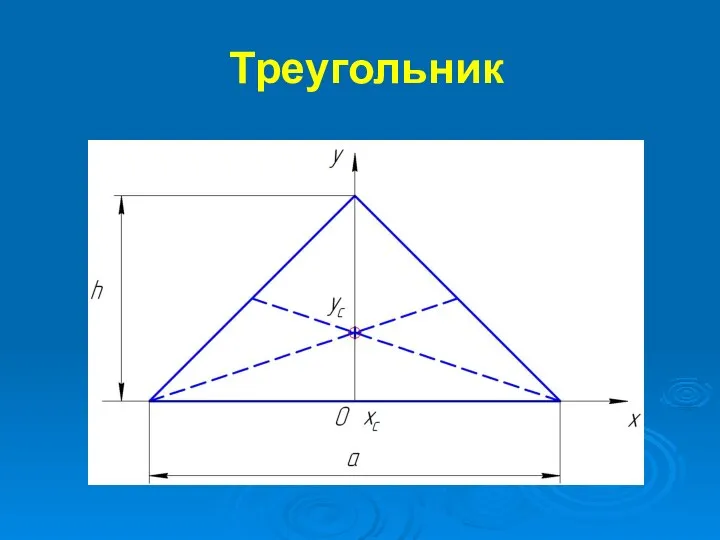
Слайд 18Где h – высота треугольника;
а – основание треугольника.

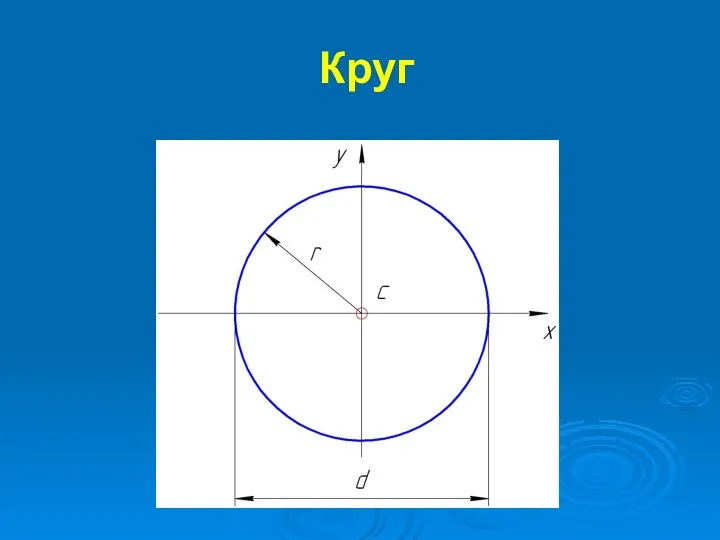
Слайд 20Где r – радиус круга;
d – диаметр круга;

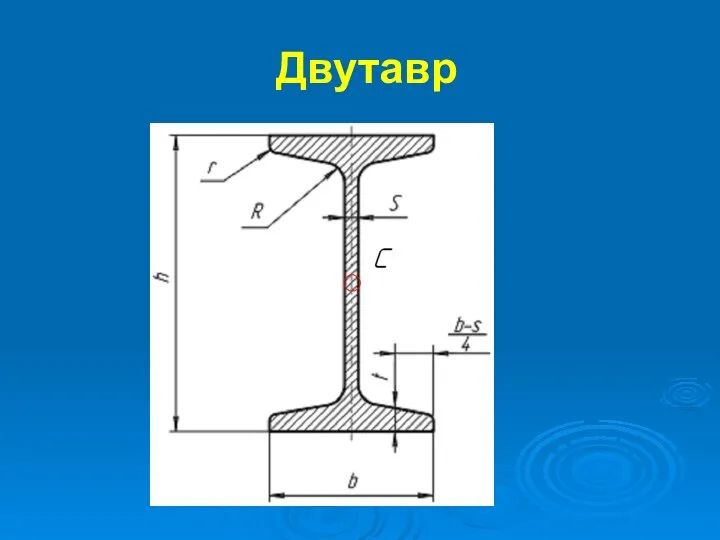
Слайд 214. Нахождение центра тяжести стандартных прокатных профилей
Двутавр;
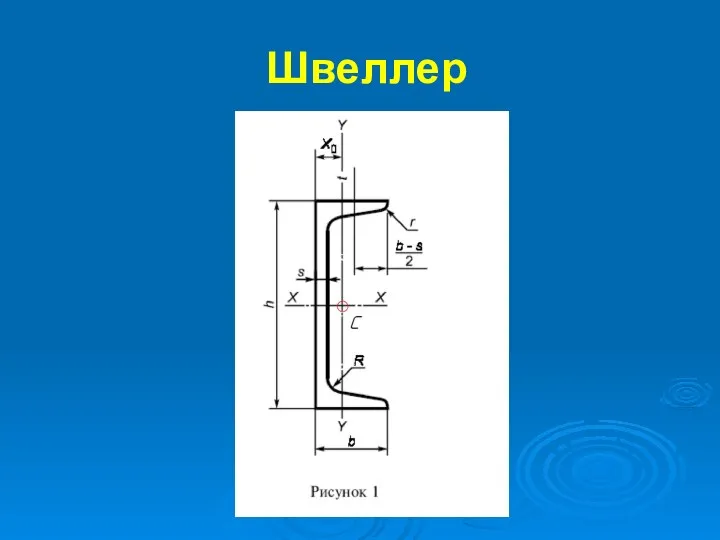
Швеллер;
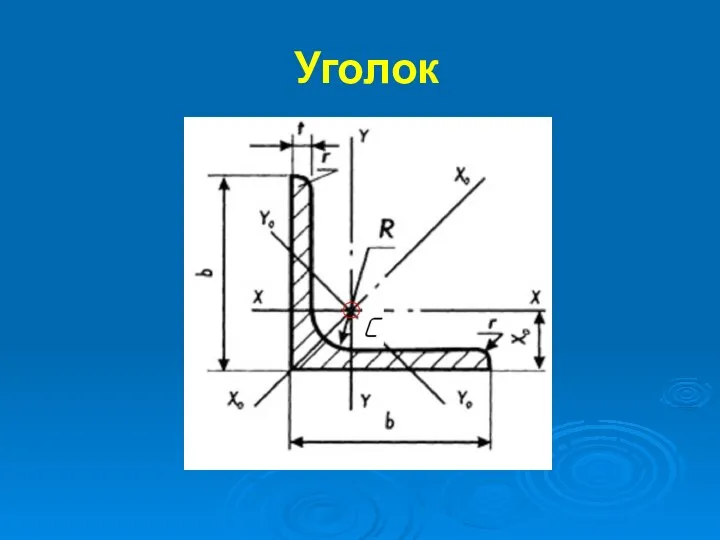
Уголок

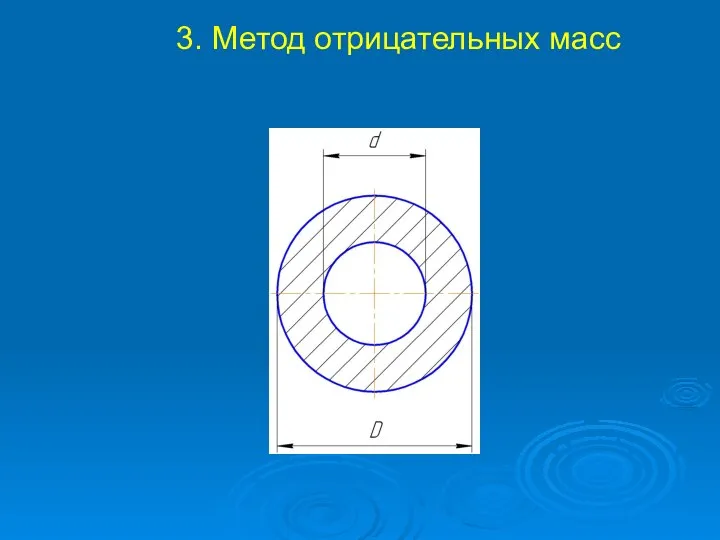
Слайд 255. Нахождение центра тяжести объемных фигур

Слайд 26Где V1- площадь первой фигуры;
V2- площадь второй фигуры;
Vn- площадь n-ой

фигуры;
Х1- координата х центра тяжести первой фигуры;
Х2- координата х центра тяжести второй фигуры;
Х3- координата х центра тяжести n-ой фигуры;
n – число частей, на которое разбито тело.

















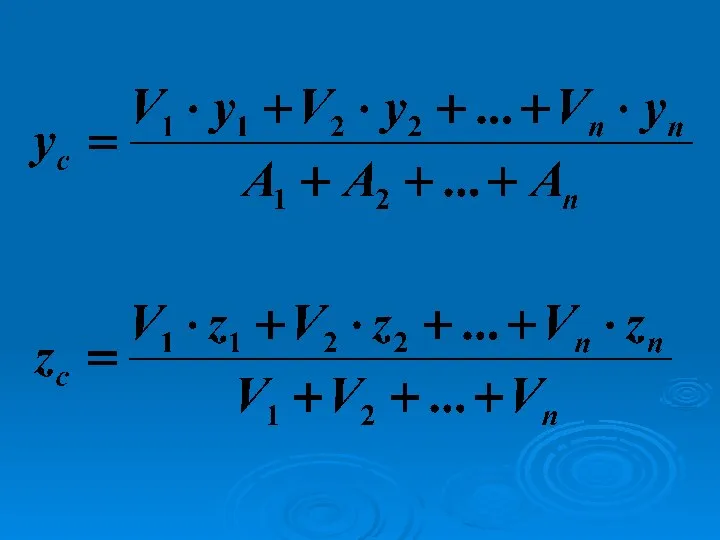
 Опиливание заготовок из металла и пластмассы
Опиливание заготовок из металла и пластмассы Решение задач ЕГЭ на закон Джоуля Ленца
Решение задач ЕГЭ на закон Джоуля Ленца Гидродинамика
Гидродинамика Звуковые волны
Звуковые волны Топливо будущего
Топливо будущего Школа юного исследователя
Школа юного исследователя Магнитостатическое поле в вакууме. Часть 3
Магнитостатическое поле в вакууме. Часть 3 Элементарная теория атома водорода по бору
Элементарная теория атома водорода по бору Свободное падение тел_ Движение с ускорением свободного падения
Свободное падение тел_ Движение с ускорением свободного падения Сила
Сила Динамика вращательного движения твердого тела
Динамика вращательного движения твердого тела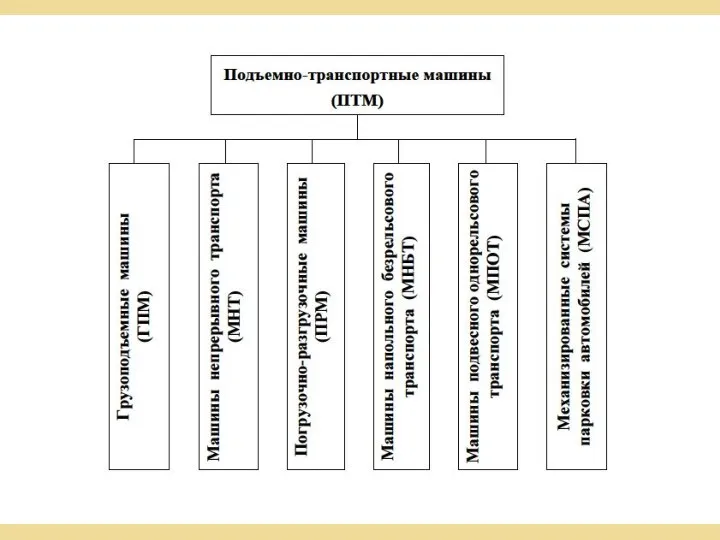 Классификация подъемно-транспортных машин
Классификация подъемно-транспортных машин Пример построения наблюдателя для системы 3-го порядка
Пример построения наблюдателя для системы 3-го порядка Презентация на тему Калейдоскоп физических явлений
Презентация на тему Калейдоскоп физических явлений  Генерирование электрической энергии. Трансформаторы. (11 класс)
Генерирование электрической энергии. Трансформаторы. (11 класс) Виды сил
Виды сил Как уменьшить силу трения
Как уменьшить силу трения Презентация на тему Дисперсия света (11 класс)
Презентация на тему Дисперсия света (11 класс) 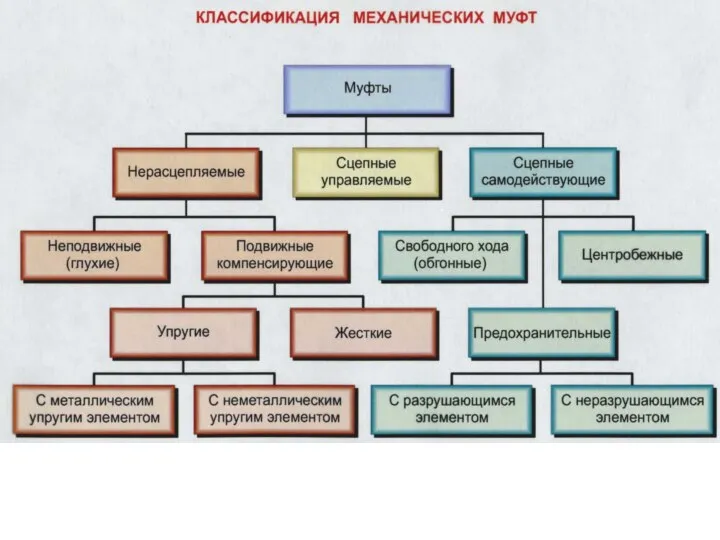 Классификация механических муфт
Классификация механических муфт Исследование изменения со временем температуры остывающей воды
Исследование изменения со временем температуры остывающей воды Радиоволны. Свойства
Радиоволны. Свойства Шредингер теңдеуін бөлшектердің стационар күйлеріне қатысты қарапайым есептеріне қолдану
Шредингер теңдеуін бөлшектердің стационар күйлеріне қатысты қарапайым есептеріне қолдану Физика атома и атомного ядра
Физика атома и атомного ядра Скорость истечения и расход жидкости для различных форм отверстий
Скорость истечения и расход жидкости для различных форм отверстий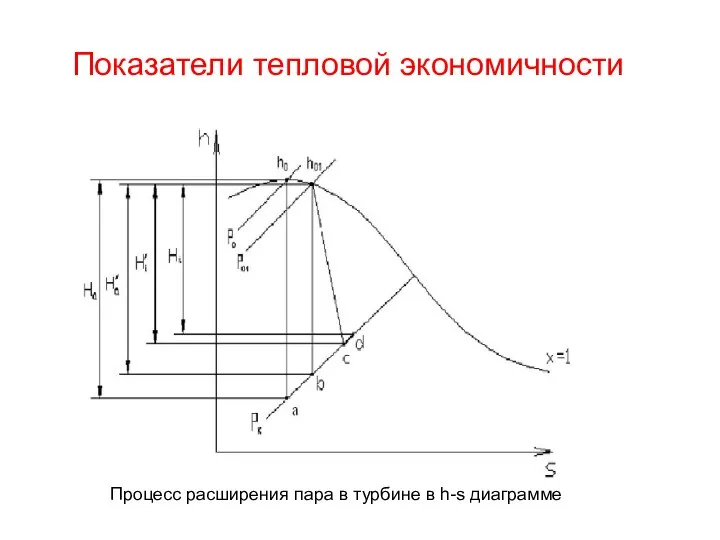 Показатели тепловой экономичности
Показатели тепловой экономичности Механическое движение (7 класс)
Механическое движение (7 класс) Классификация физико- химических методов исследования. Лекция №2
Классификация физико- химических методов исследования. Лекция №2 Открытый урок по физике в 9 классе. Явление электромагнитной индукции МОУ «СОШ №19» Г.о. Электросталь
Открытый урок по физике в 9 классе. Явление электромагнитной индукции МОУ «СОШ №19» Г.о. Электросталь