Содержание
- 2. Дифракция света Часть 1 Дифракция Френеля Принцип Гюйгенса – Френеля. Метод зон Френеля. Применение векторных диаграмм
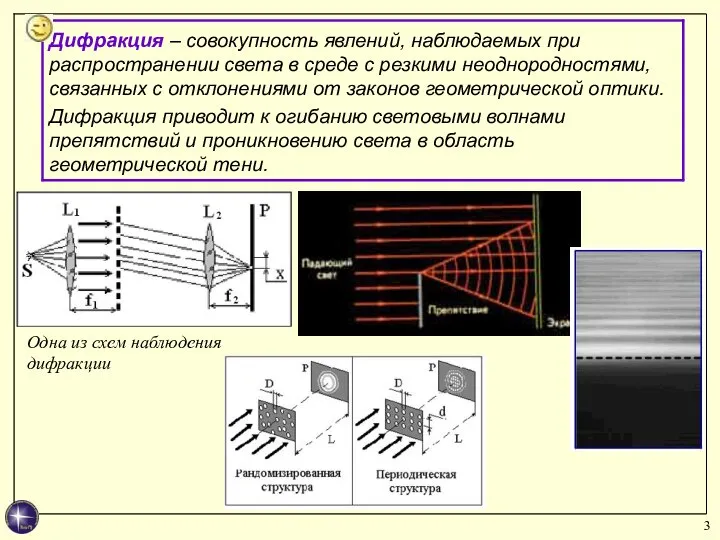
- 3. Одна из схем наблюдения дифракции
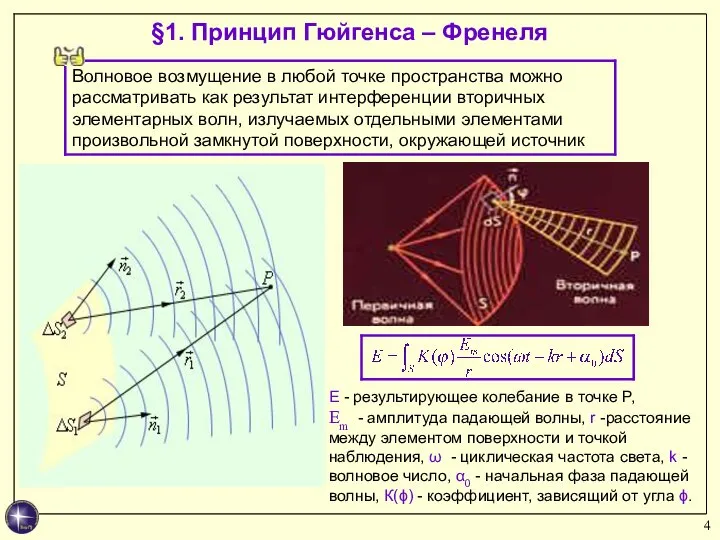
- 4. §1. Принцип Гюйгенса – Френеля Е - результирующее колебание в точке P, Em - амплитуда падающей
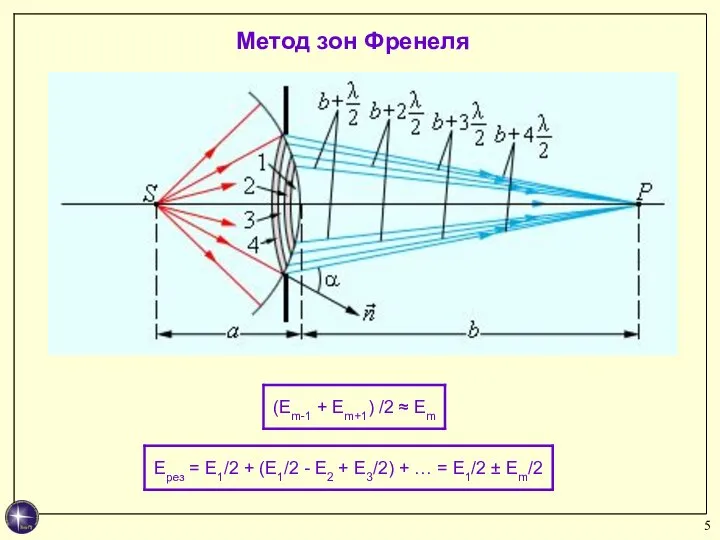
- 5. Метод зон Френеля
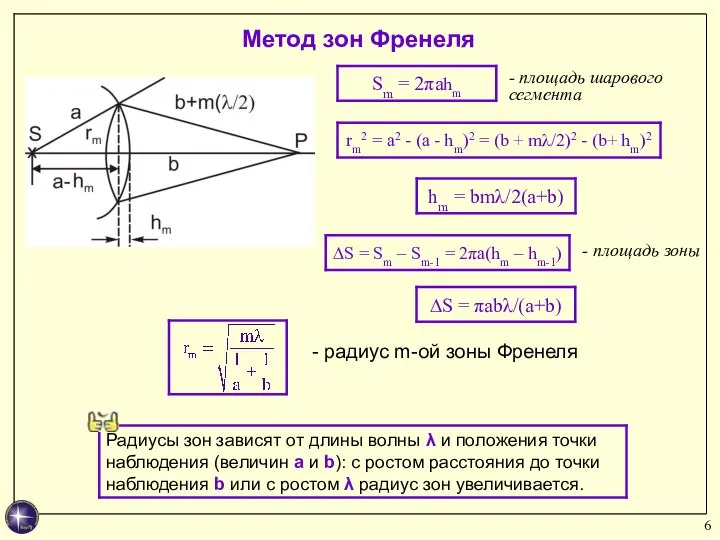
- 6. Метод зон Френеля - радиус m-ой зоны Френеля - площадь зоны - площадь шарового сегмента
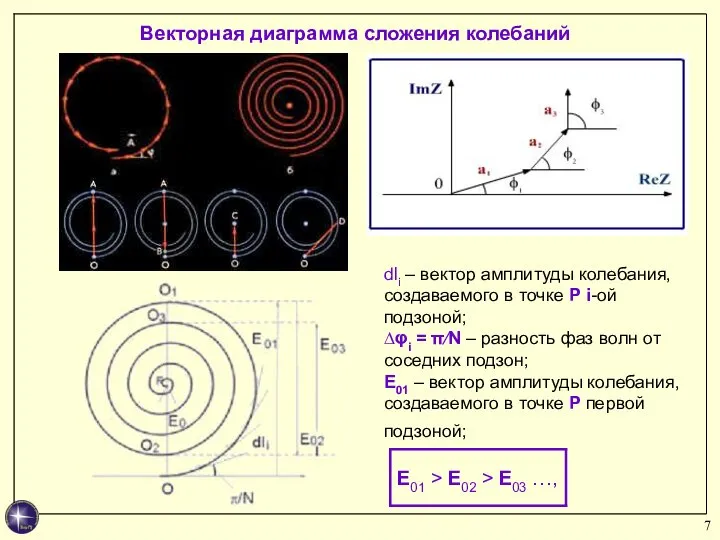
- 7. Векторная диаграмма сложения колебаний dli – вектор амплитуды колебания, создаваемого в точке P i-ой подзоной; ∆φi
- 9. Различные задачи дифракции 1. Полностью открытый волновой фронт
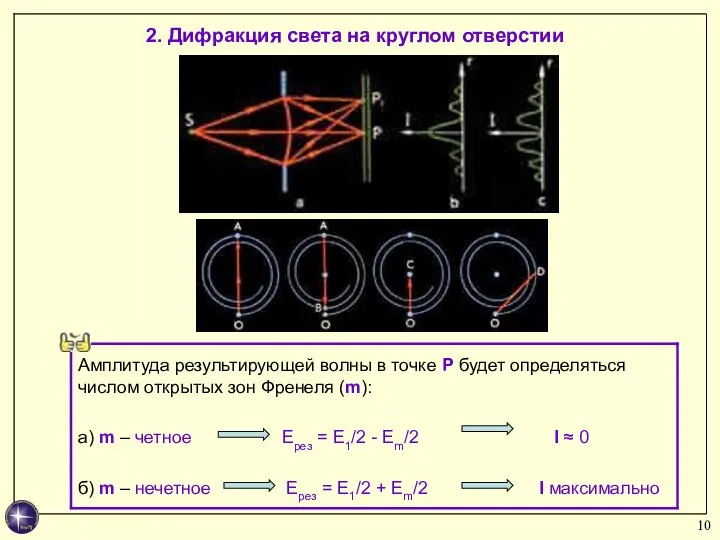
- 10. 2. Дифракция света на круглом отверстии
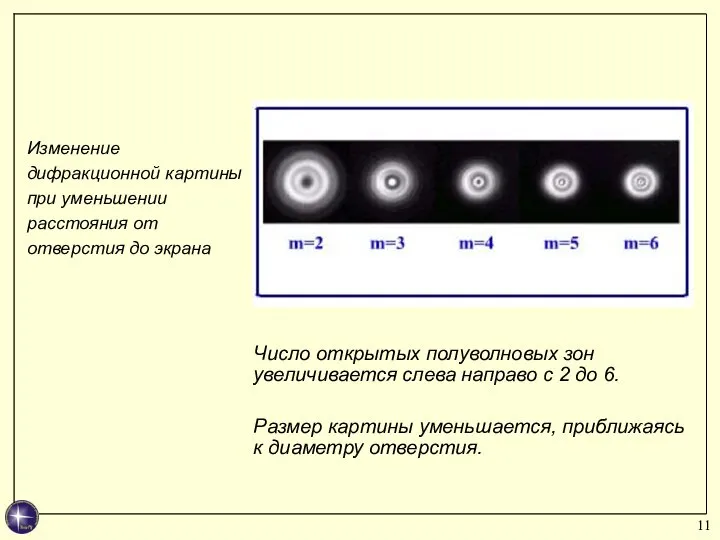
- 11. Число открытых полуволновых зон увеличивается слева направо с 2 до 6. Размер картины уменьшается, приближаясь к
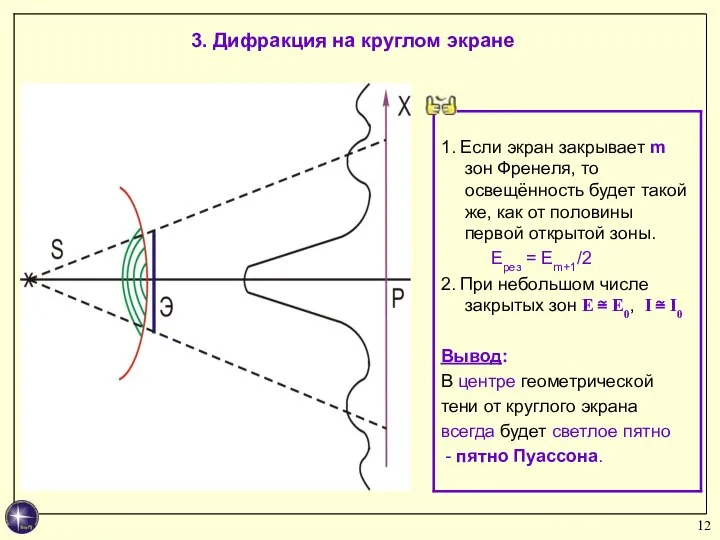
- 12. 3. Дифракция на круглом экране
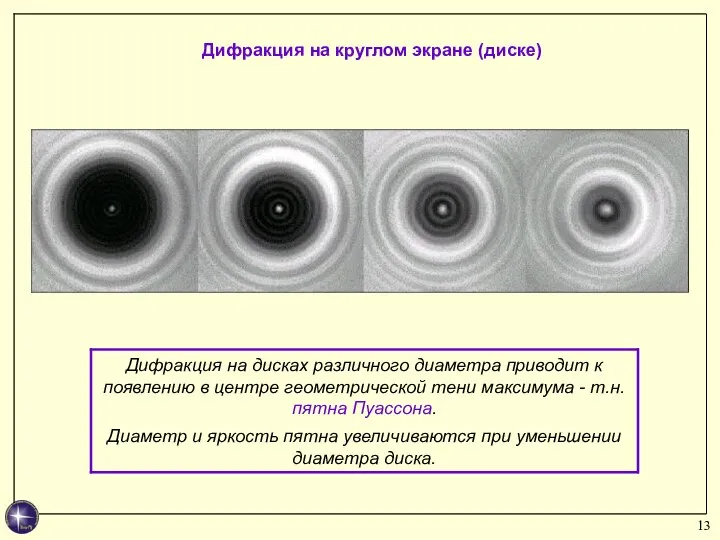
- 13. Дифракция на круглом экране (диске)
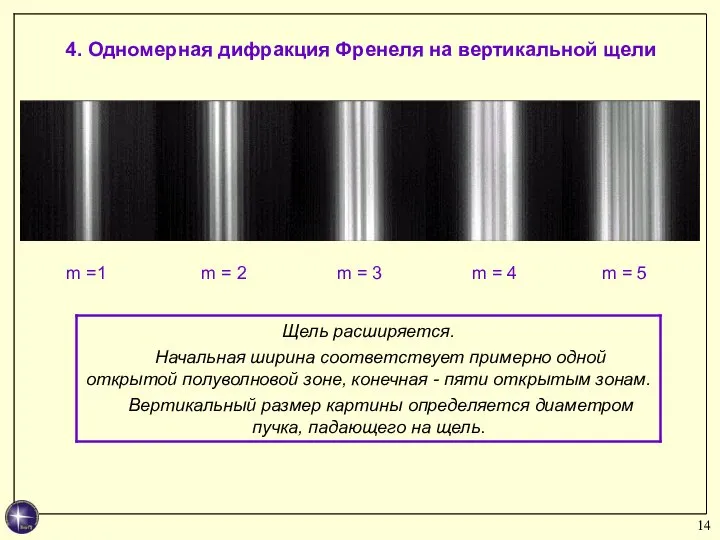
- 14. 4. Одномерная дифракция Френеля на вертикальной щели m =1 m = 2 m = 3 m
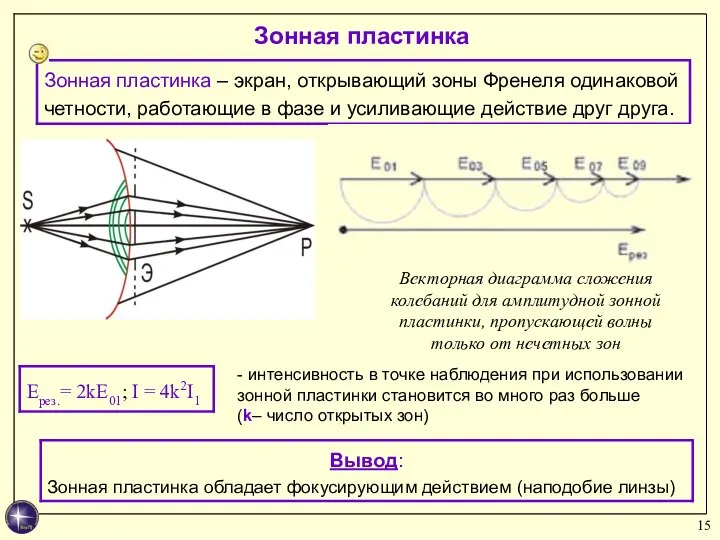
- 15. Зонная пластинка Векторная диаграмма сложения колебаний для амплитудной зонной пластинки, пропускающей волны только от нечетных зон
- 16. – формула зонной пластинки f – главное фокусное расстояние зонной пластинки
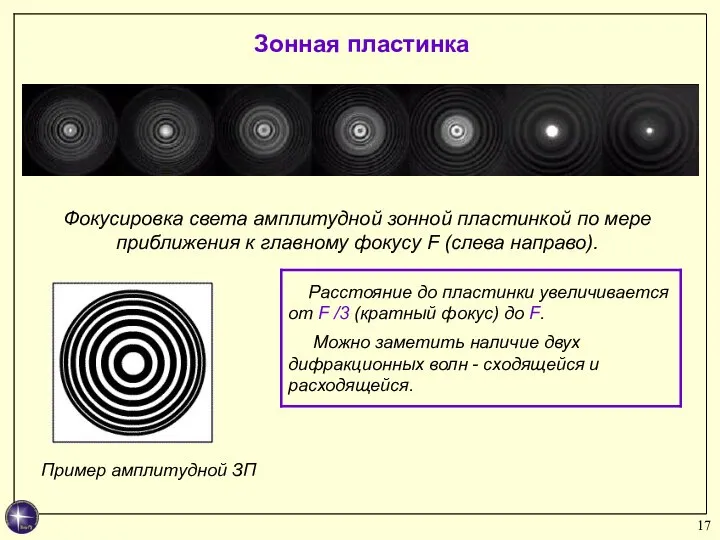
- 17. Фокусировка света амплитудной зонной пластинкой по мере приближения к главному фокусу F (слева направо). Зонная пластинка
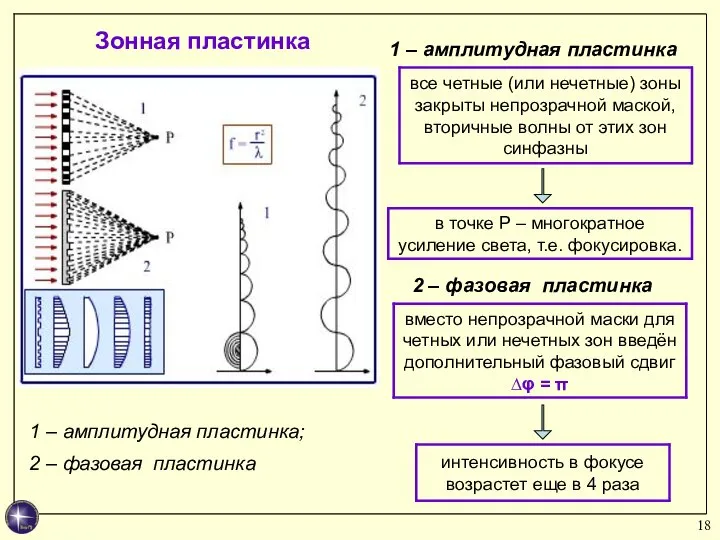
- 18. Зонная пластинка 1 – амплитудная пластинка; 2 – фазовая пластинка 1 – амплитудная пластинка 2 –
- 19. Дифракция Фраунгофера Условия, позволяющие пользоваться законами геометрической оптики Дифракция Фраунгофера. Схема наблюдения Дифракция Фраунгофера на щели
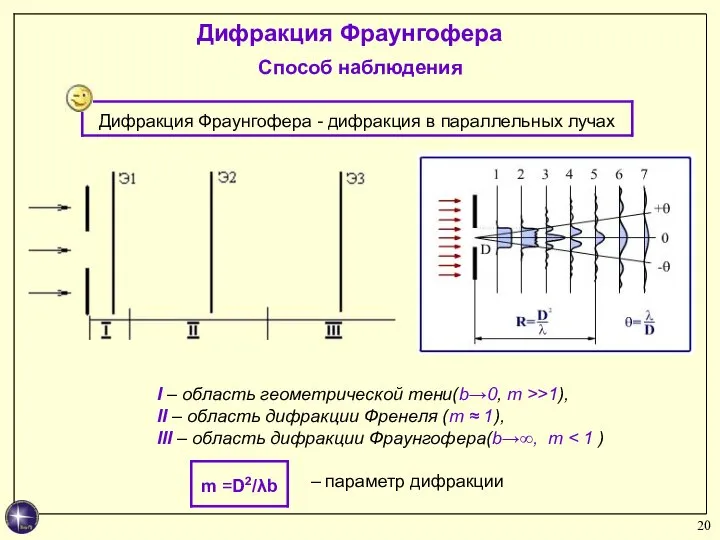
- 20. Дифракция Фраунгофера Способ наблюдения I – область геометрической тени(b→0, m >>1), II – область дифракции Френеля
- 21. Условия, позволяющие пользоваться законами геометрической оптики - радиус экрана R порядка радиуса первой зоны Френеля (при
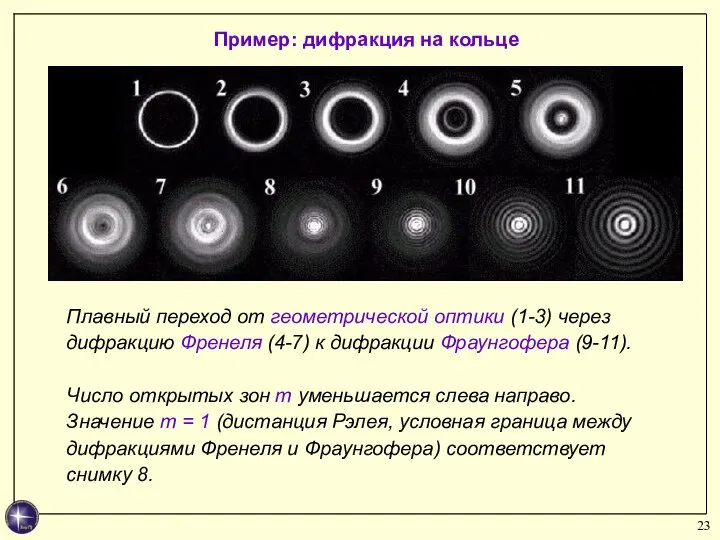
- 23. Плавный переход от геометрической оптики (1-3) через дифракцию Френеля (4-7) к дифракции Фраунгофера (9-11). Число открытых
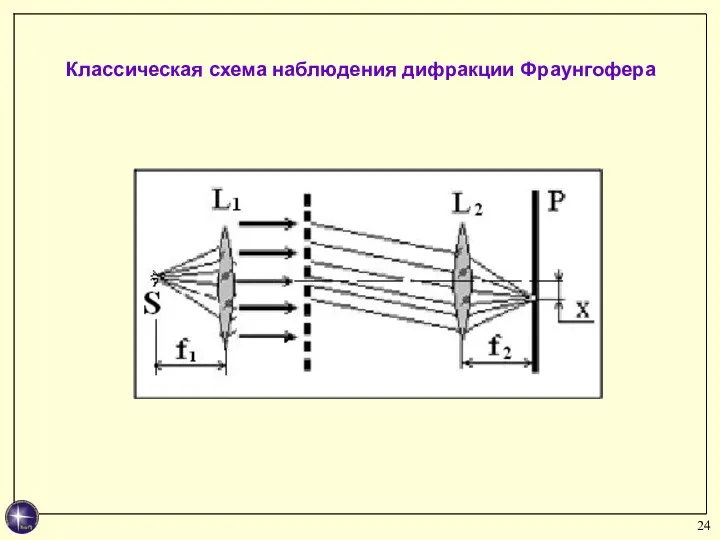
- 24. Классическая схема наблюдения дифракции Фраунгофера
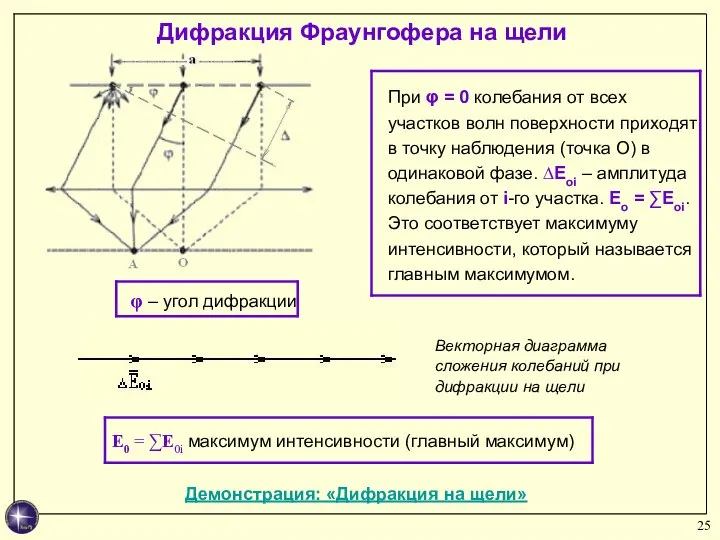
- 25. Дифракция Фраунгофера на щели Демонстрация: «Дифракция на щели» Векторная диаграмма сложения колебаний при дифракции на щели
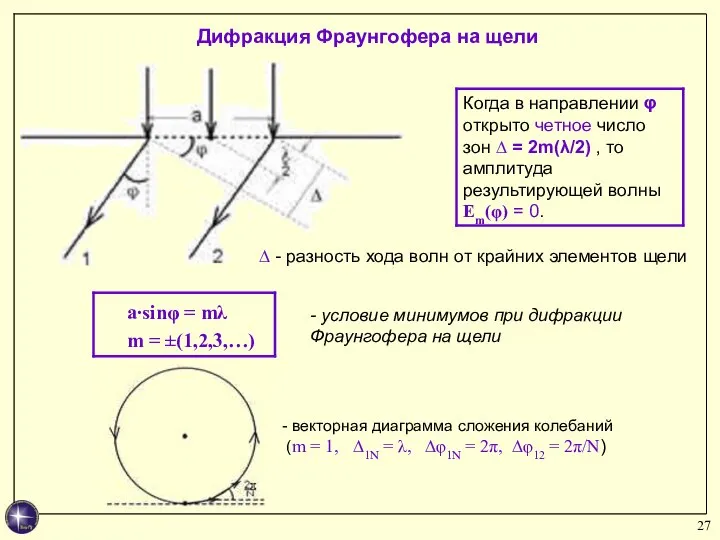
- 26. Дифракция Фраунгофера на щели
- 27. - условие минимумов при дифракции Фраунгофера на щели - векторная диаграмма сложения колебаний (m = 1,
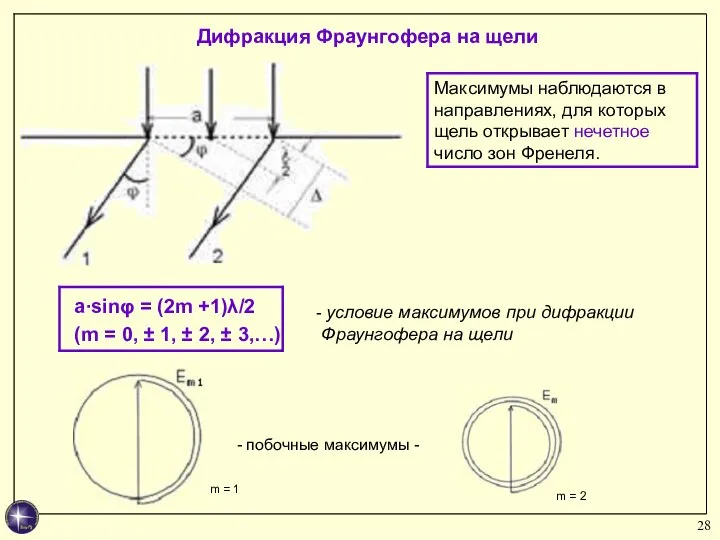
- 28. условие максимумов при дифракции Фраунгофера на щели m = 1 m = 2 побочные максимумы -
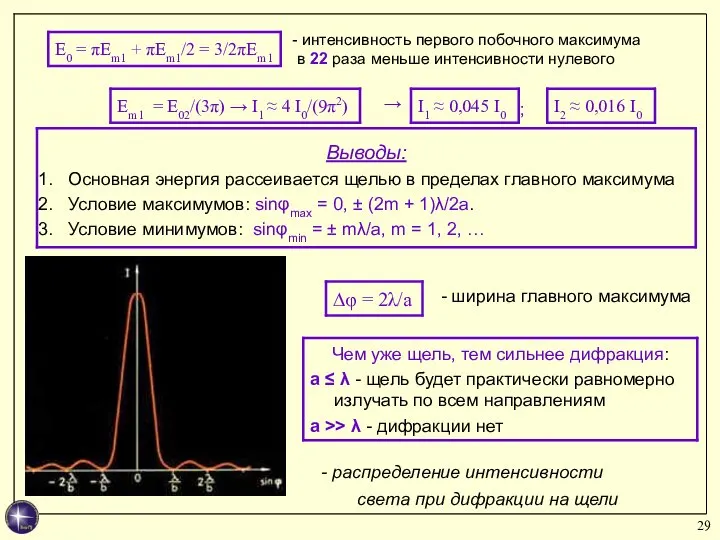
- 29. интенсивность первого побочного максимума в 22 раза меньше интенсивности нулевого → ; - распределение интенсивности света
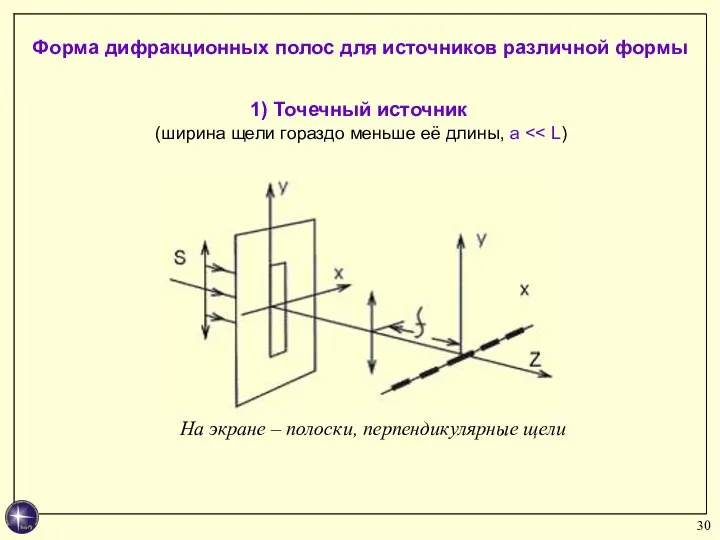
- 30. 1) Точечный источник (ширина щели гораздо меньше её длины, a Форма дифракционных полос для источников различной
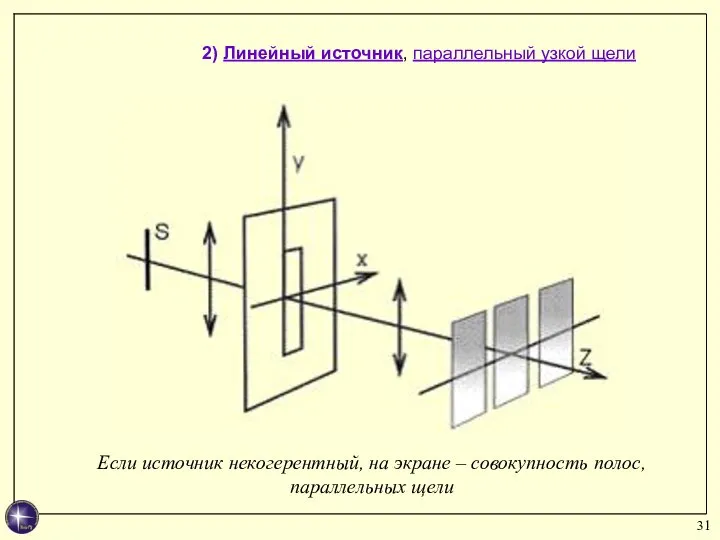
- 31. 2) Линейный источник, параллельный узкой щели Если источник некогерентный, на экране – совокупность полос, параллельных щели
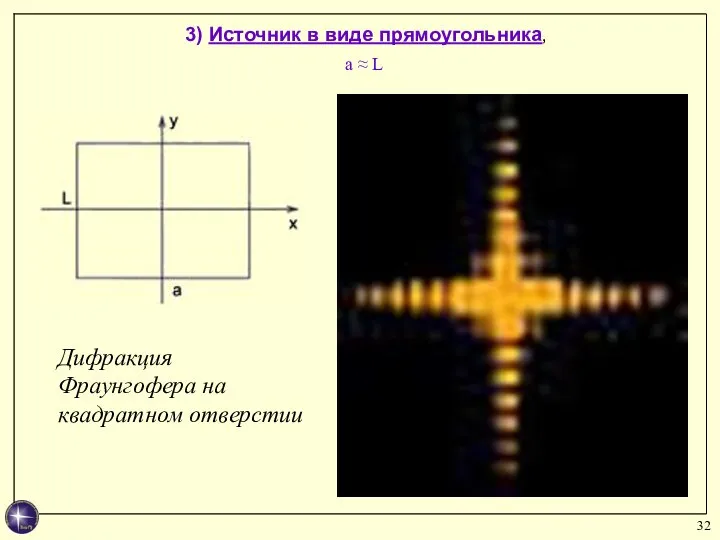
- 32. 3) Источник в виде прямоугольника, a ≈ L Дифракция Фраунгофера на квадратном отверстии
- 33. Картина дифракции Фраунгофера на круглом отверстии 4) Дифракция Фраунгофера на круглом отверстии , m =1, 2,
- 34. R – радиус отверстия, φm – направление на m-ый минимум, φ′m - направление на m-ый максимум,
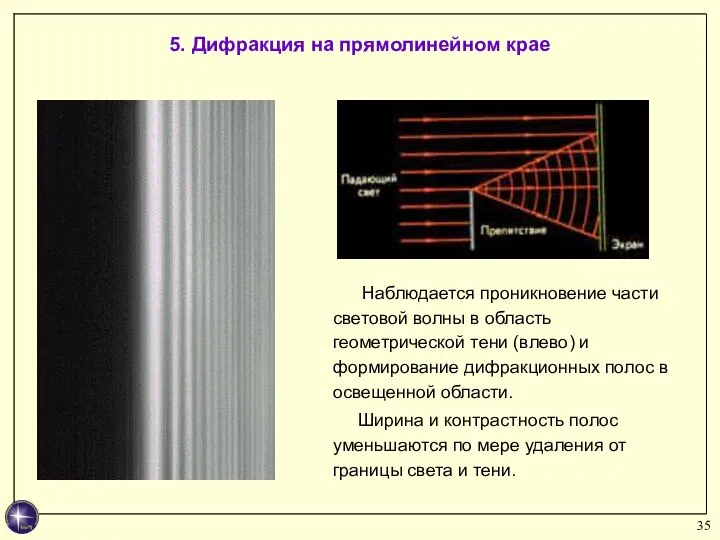
- 35. 5. Дифракция на прямолинейном крае Наблюдается проникновение части световой волны в область геометрической тени (влево) и
- 36. Опыты Аркадьева В. Н. - условие подобия дифракционных картин (m1 = m2) раза. Метод подобия
- 37. Дифракция на многих беспорядочно расположенных преградах Изучается самостоятельно
- 39. Скачать презентацию












 Велосипед: из чего состоит и его характеристики
Велосипед: из чего состоит и его характеристики Явление электромагнитной индукции
Явление электромагнитной индукции Основы динамики
Основы динамики Обобщающий урок по теме « Электростатика» Цели урока: образовательные: Формирование и систематизация первоначальных пре
Обобщающий урок по теме « Электростатика» Цели урока: образовательные: Формирование и систематизация первоначальных пре Мероприятия по усилению конструкции фюзеляжа вертолета Ми-8МТ
Мероприятия по усилению конструкции фюзеляжа вертолета Ми-8МТ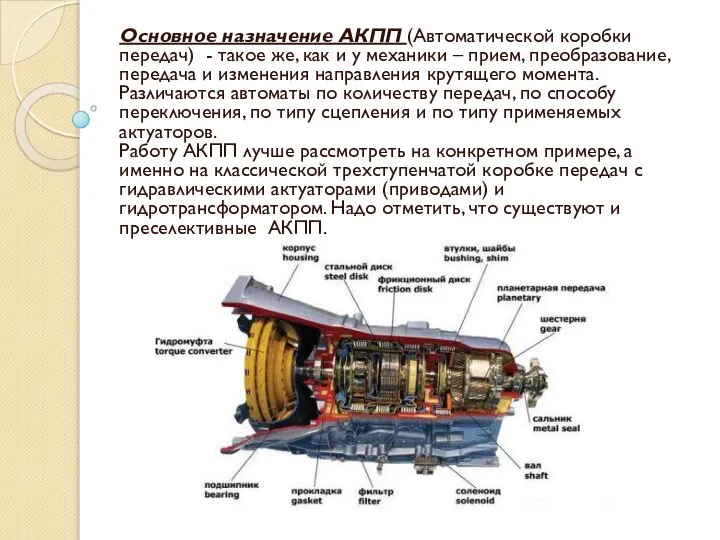 obshchee-ustroystvo-i-printsip-raboty-akpp
obshchee-ustroystvo-i-printsip-raboty-akpp Контакт волнистых и шероховатых тел
Контакт волнистых и шероховатых тел Физические и химические явления. Признаки химических реакций
Физические и химические явления. Признаки химических реакций lektsia
lektsia Автоматическое управление процессом электролиза
Автоматическое управление процессом электролиза Статика
Статика Визуальный и измерительный метод неразрушающего контроля. Электронный учебный курс
Визуальный и измерительный метод неразрушающего контроля. Электронный учебный курс 6. Механика жидкости и газа.ppt
6. Механика жидкости и газа.ppt Альтернативные источники энергии
Альтернативные источники энергии Строение вещества
Строение вещества Законы геометрической оптики
Законы геометрической оптики Работа и энергия
Работа и энергия Основы термодинамики
Основы термодинамики Расчет концентрационных пределов воспламенения жидкости
Расчет концентрационных пределов воспламенения жидкости Полупроводники
Полупроводники Електричне поле. Одна шз складових електромагнітого поля
Електричне поле. Одна шз складових електромагнітого поля 9 кл Механическое дв-ние
9 кл Механическое дв-ние Термоэлектрогенератор. Принцип работы термоэлектрогенератора
Термоэлектрогенератор. Принцип работы термоэлектрогенератора Туннельный диод
Туннельный диод Электрические машины
Электрические машины Классический эффект Холла
Классический эффект Холла Движение тела по окружности под действием силы тяжести
Движение тела по окружности под действием силы тяжести Примеры некорректных задач. Уравнения математической физики. Режимы с обострением
Примеры некорректных задач. Уравнения математической физики. Режимы с обострением