Содержание
- 2. План занятия. 1. Микропараметры и макропараметры. 2. Уравнение состояния идеального газа. 3. Давление газа на стенки
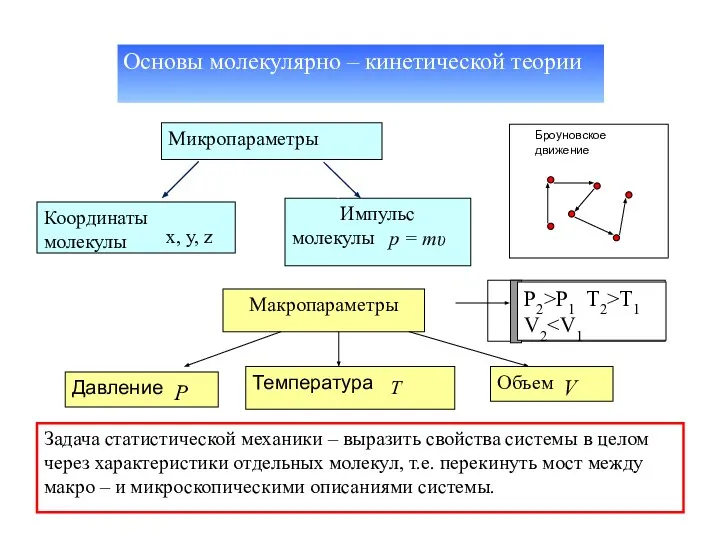
- 3. Основы молекулярно – кинетической теории Микропараметры Координаты молекулы Импульс молекулы x, y, z p = mυ
- 4. Уравнение состояния идеального газа Идеальный газ – газ, взаимодействием молекул которого можно пренебречь. Соотношение, определяющее связь
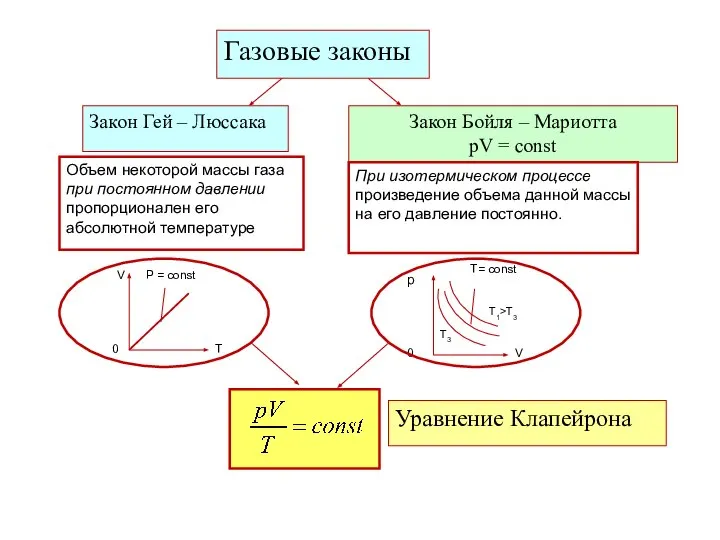
- 5. Газовые законы Закон Гей – Люссака Закон Бойля – Мариотта pV = const Объем некоторой массы
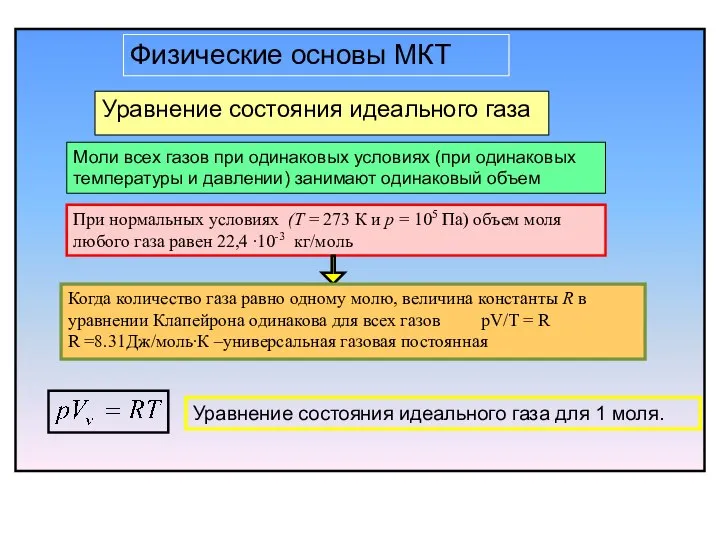
- 6. Уравнение состояния идеального газа Моли всех газов при одинаковых условиях (при одинаковых температуры и давлении) занимают
- 7. Уравнение Менделеева -Клапейрона Умножим и разделим правую часть на число Авогадро NA - Число молекул в
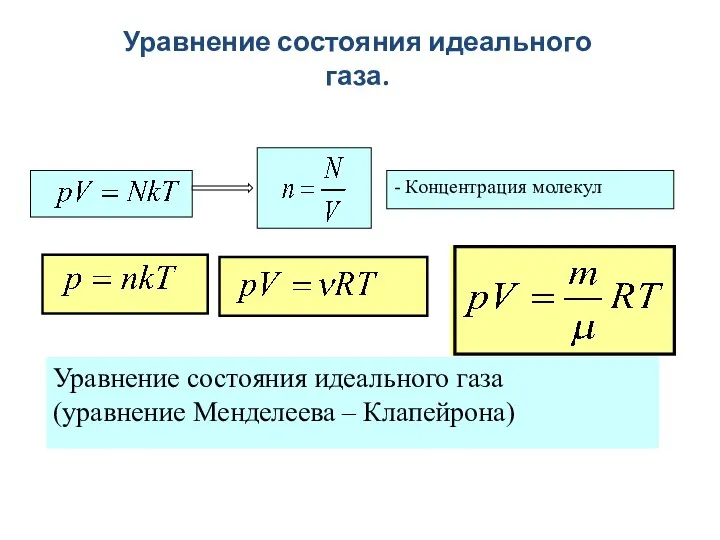
- 8. Уравнение состояния идеального газа.
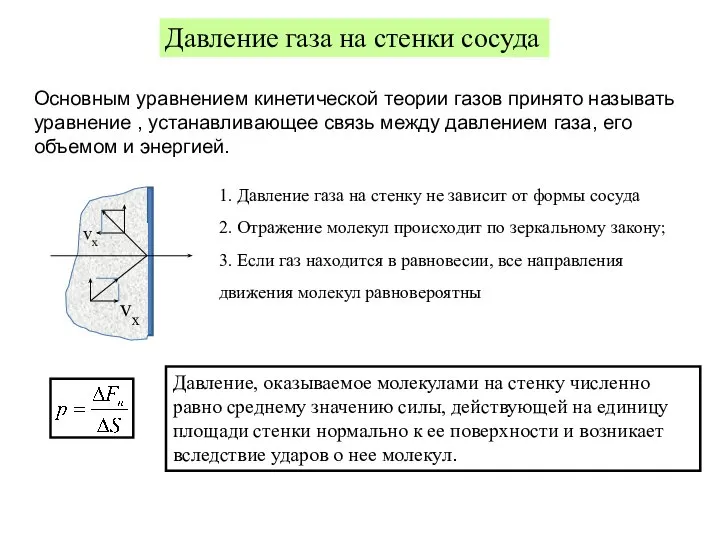
- 9. Термодинамические параметры и процессы Давление газа на стенки сосуда Основным уравнением кинетической теории газов принято называть
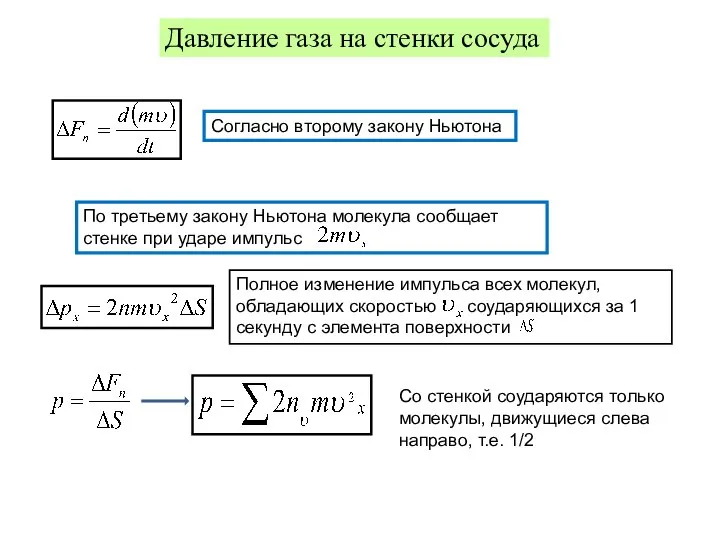
- 10. Термодинамические параметры и процессы Давление газа на стенки сосуда Согласно второму закону Ньютона Полное изменение импульса
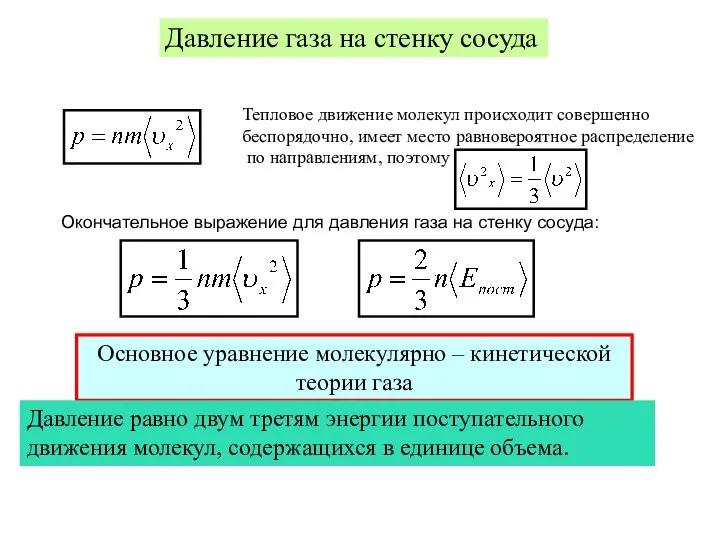
- 11. Термодинамические параметры и процессы Давление газа на стенку сосуда Тепловое движение молекул происходит совершенно беспорядочно, имеет
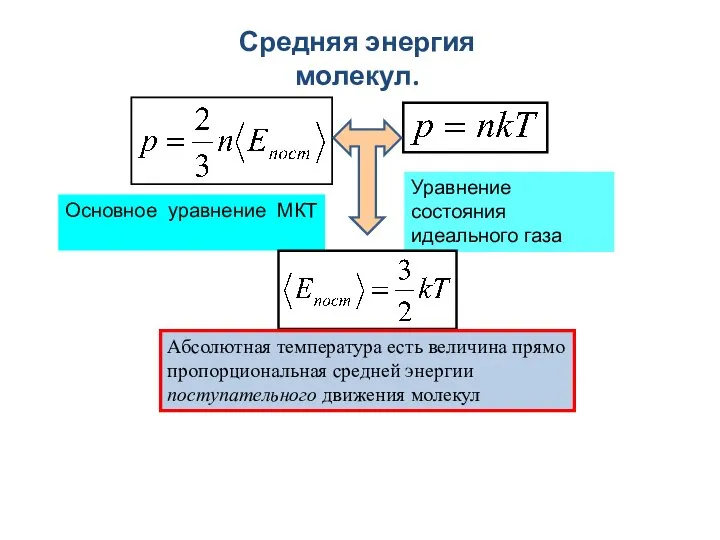
- 12. Средняя энергия молекул. Основное уравнение МКТ Уравнение состояния идеального газа Абсолютная температура есть величина прямо пропорциональная
- 13. Степени свободы сложной системы. Средняя энергия зависит только от температуры и не зависит от массы молекулы
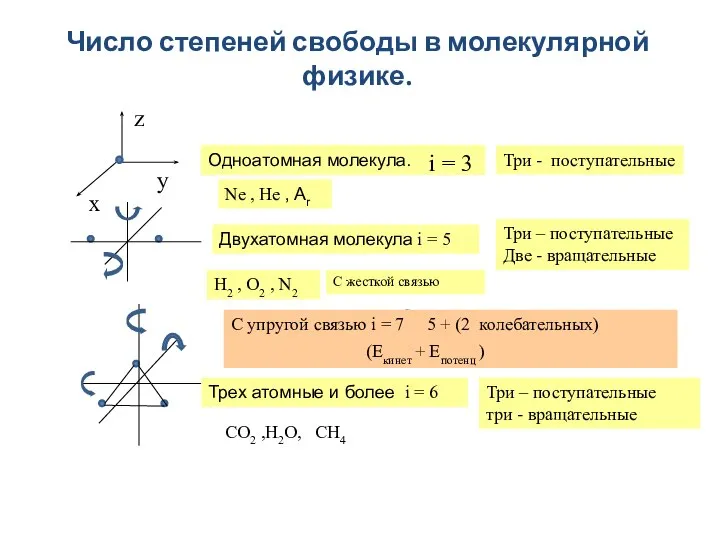
- 14. Число степеней свободы в молекулярной физике. x y z Одноатомная молекула. i = 3 Двухатомная молекула
- 15. Закон распределения энергии На каждую степень свободы (поступательную, вращательную и колебательную) в среднем приходится одинаковая кинетическая
- 16. Примеры и задачи Задача 1 Сколько атомов водорода содержится в 50 г водяного пара? Решение Число
- 17. Примеры и задачи Задача 3 Определить число n молекул воздуха в единице объема при температуре 00С
- 18. Примеры и задачи Задача 5 Какое давление на стенки сосуда производят 0,02 кг кислорода, занимающего объем
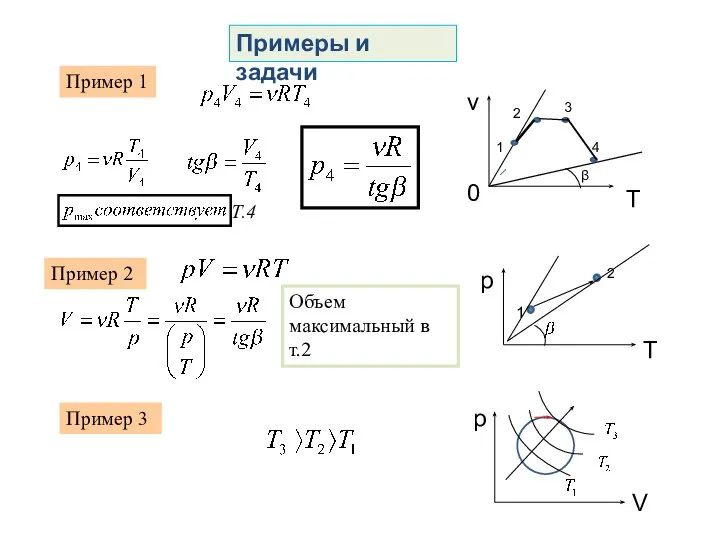
- 19. Примеры и задачи Пример 1 В сосуде, закрытом поршнем, находится идеальный газ. График зависимости объема газа
- 20. Примеры и задачи Пример 1 1 2 3 4 β Т.4 Пример 2 Объем максимальный в
- 22. Скачать презентацию









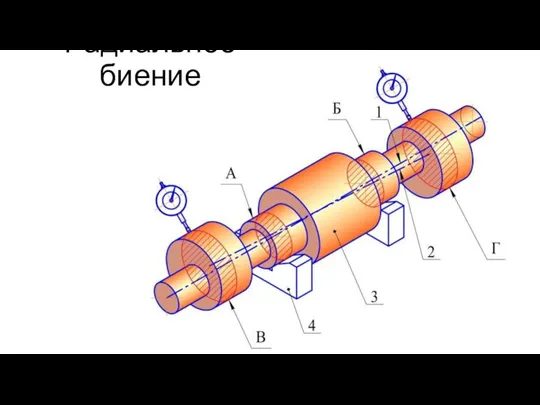 Радиальное биение
Радиальное биение Состав ядра атома. Энергия связи атомных ядер. Дефект масс
Состав ядра атома. Энергия связи атомных ядер. Дефект масс Презентация на тему Принцип относительности в механике. Постулаты теории относительности (11 класс)
Презентация на тему Принцип относительности в механике. Постулаты теории относительности (11 класс)  История возникновения квантовой физики
История возникновения квантовой физики Электроника
Электроника Блоки. Простые механизмы
Блоки. Простые механизмы Результаты измерений. Лабораторная работа №3 по биофизике
Результаты измерений. Лабораторная работа №3 по биофизике Трехфазные цепи
Трехфазные цепи Сила тяжіння. Вага тіла. Невагомість
Сила тяжіння. Вага тіла. Невагомість Интерференция света
Интерференция света Решение экспериментальных задач
Решение экспериментальных задач Стабильность градуировочных графиков, их роль в оценке качества количественного химического анализа
Стабильность градуировочных графиков, их роль в оценке качества количественного химического анализа Прямолинейное равноускоренное движение. Ускорение
Прямолинейное равноускоренное движение. Ускорение Презентация на тему Построение изображений в линзах
Презентация на тему Построение изображений в линзах  Ядерный реактор
Ядерный реактор Фазовые и структурные превращения в оболочках ТВЭЛов из сплава Э110 в условиях сухого хранения
Фазовые и структурные превращения в оболочках ТВЭЛов из сплава Э110 в условиях сухого хранения Основные положения молекулярно-кинетической теории
Основные положения молекулярно-кинетической теории Все о звуке
Все о звуке Метрология
Метрология § 4. Физические величины. Измерение физических величин
§ 4. Физические величины. Измерение физических величин Оценкауровня электромагнитных излучений от бытовой электроники
Оценкауровня электромагнитных излучений от бытовой электроники Статика. Решение задач на равновесие твердого тела
Статика. Решение задач на равновесие твердого тела Изделие и техническая информация о нем
Изделие и техническая информация о нем Шуми оптико-електронних систем. Лекція 5
Шуми оптико-електронних систем. Лекція 5 5 урок свободное падение тела
5 урок свободное падение тела Машины и оборудование, инженерные системы и энергосберегающие технологии в городском хозяйстве и сфере услуг
Машины и оборудование, инженерные системы и энергосберегающие технологии в городском хозяйстве и сфере услуг Гидравлические машины
Гидравлические машины Технические измерения
Технические измерения