Содержание
- 2. Теорема Найквиста—Шеннона—Котельникова Теорема гласит (упрощенно), что для сигнала, представленного последовательностью дискретных отсчетов, точное восстановление возможно, только
- 3. Итак, согласно теореме, рассматривающей идеальные условия, частота дискретизации, с которой следует брать отсчеты, составляет не менее
- 4. История вопроса об основополагающей теореме взятия отсчетов Хотя в западной литературе теорема часто называется теоремой Найквиста
- 5. Из теоремы Котельникова следует, что при дискретизации аналогового сигнала потерь информации не будет только в том
- 6. При доказательстве теоремы Котельникова взяты ограничения на спектр частот 0 Такая трактовка рассматривает идеальный случай, когда
- 7. Элементы приемника данных (контроля моделируемой схемы и вывода данных из точек анализа) BeamMeasurement Part BER FER
- 8. Приемник данных (универсальный вывод данных) Description: Data Sink Domain: Timed C++ Code Generation Support: NO SystemVueEngine
- 10. Анализаторы спектра. Общие сведения По диапазону частот — низкочастотные, радиодиапазона (широкополосные) и оптического диапазона. По принципу
- 11. Низкочастотные анализаторы НЧ анализаторы бывают параллельного и последовательного типа (чаще параллельного) и предназначены для работы в
- 12. Анализаторы параллельного типа Анализаторы параллельного типа содержат набор идентичных узкополосных фильтров (высокодобротных резонаторов), каждый из которых
- 13. Анализатор спектра комплексной огибающей сигналов Модель анализатора спектра может быть использована для измерения спектра действительной составляющей
- 14. Примечания к анализатору комплексной огибающей сигнала Анализатор спектра имеет два режима работы: Time Gate и ResBW.
- 15. Примечания к анализатору комплексной огибающей сигнала При обработке и усреднении нескольких сегментов усреднение фаз (для тонов,
- 16. Оконная обработка Оконные окна необходимы при оценке спектра на основе преобразования (БПФ). Без оконного отображения расчетный
- 17. Рекомендации по применению типов окон Не используйте окно (установите окно на Равномерное) при анализе переходных процессов.
- 18. Аналитические выражения для весовых функций (окон) Когда сигнал временной области обрабатывается окном, отличным от прямоугольного, его
- 19. Параметр Persistence можно использовать для уменьшения размера файла рабочей области, не сохраняя переменные, генерируемые этой моделью
- 21. Запись данных моделирования в файл
- 22. Опции компонента записи в файл Данная модель записывает реальную и мнимую части комплексных данных в файлы
- 23. Формат N6030 записи данных в файл N6030 считывает данные I и Q из файла и файла
- 24. Динамические графики Окно Dynamic Graphs (Динамических графиков) относится к отдельному окну, которое автоматически открывается при некотором
- 26. Компонент оценок величины вектора ошибок измерений Эта модель используется для выполнения измерения EVM (Величины вектора ошибки)
- 27. Сумма квадратов вектора ошибок равна: где N равно ResultLength и C0, C1, W выбираются таким образом,
- 28. Параметр Start задает время начала сбора данных. Убедитесь, что вы установили Start, чтобы избежать любых переходных
- 29. Параметры MeasurementFilter и ReferenceFilter определяют, какая фильтрация будет выполняться на входе и внутри сгенерированных опорных сигналах.
- 30. Модель EVM работает с сигналами, которые представляют собой ОДНУ модулированную несущую. Когда входной сигнал включает в
- 31. Результаты измерений, сохраненные в наборе данных, описаны ниже. EVM_RMS: Значение EVM_RMS, выражается в %. EVM_Peak: максимальное
- 32. Если параметр ContinuousMode установлен в значение ДА, то графики будут динамически обновляться на протяжении всего моделирования.
- 33. Глазковая диаграмма Эта модель создает динамический график, отображающий глазковую диаграмму входного сигнала. Параметр SymbolRate определяет частоту
- 34. Основы глазковой диаграммы: чтение и применение глазковых диаграмм Увеличение скоростей передачи данных, бо́льшая сложность проектирования, требования
- 35. Получение глазковой диаграммы Глазковая диаграмма – это распространенный индикатор качества сигналов в высокоскоростных цифровых системах передачи.
- 36. Интерпретация глазковой диаграммы Правильно построенный глаз должен содержать каждую возможную битовую последовательность от простых чередующихся единиц
- 37. Джиттер Хотя теоретически глазковые диаграммы должны выглядеть как прямоугольные коробки, конечное время нарастания и спада сигналов
- 38. На сгенерированных глазковых диаграммах хорошо виден эффект разрыва. При неправильной нагрузке конца линии глаз выглядит ограниченным
- 39. Как видно на рисунке, глазковая диаграмма может показать важную информацию. Она может указывать лучшую точку для
- 40. CCDF_Cx Модель CCDF_Cx вычисляет комплементарную кумулятивную функцию распределения (CCDF) сложного сигнала. Расчет CCDF описан ниже: Вычислите
- 42. Скачать презентацию
Слайд 2Теорема Найквиста—Шеннона—Котельникова
Теорема гласит (упрощенно), что для сигнала, представленного последовательностью дискретных отсчетов, точное
Теорема Найквиста—Шеннона—Котельникова
Теорема гласит (упрощенно), что для сигнала, представленного последовательностью дискретных отсчетов, точное

Из сказанного следует, что восстановить без искажений можно только сигнал, спектр которого ограничен некоторой частотой Fmax (частота Найквиста).
Однако, теоретически все реальные сигналы имеют бесконечные спектры. Спектры реальных сигналов, хотя и не бесконечны, но могут быть очень широкими. Для того чтобы при дискретизации избежать искажений, вызванных этим обстоятельством, сигнал вначале пропускают через фильтр, подавляющий в нем частоты, превышающие заданное значение Fmax, и лишь затем производят дискретизацию:
Слайд 3Итак, согласно теореме, рассматривающей идеальные условия, частота дискретизации, с которой следует брать
Итак, согласно теореме, рассматривающей идеальные условия, частота дискретизации, с которой следует брать

На картинке ниже: в случае A. частота сэмплирования fs равна частоте синусоидальной волны f. Поэтому, здесь отсчет берется один раз за цикл. В результате реконструкции получается прямая
В случае B: fs = 7/4f, или 7 отсчетов на 4 цикла волны. В этом случае восстановленный сигнал будет отличаться от исходного — 3 цикла вместо четырех.
В случае C: увеличение частоты сэмплирования до fs = 2f позволит получить сигнал той же частоты, что и исходный. Однако, если сдвинуть сигнал по фазе, мы увидим, что амплитуды исходного и восстановленного сигнала могут отличаться. Только увеличение частоты сэмплирования до значений, значительно больших f, например, fs = 10f (10 отсчетов за цикл), позволит точно восстановить сигнал (случай D).
Слайд 4История вопроса об основополагающей теореме взятия отсчетов
Хотя в западной литературе теорема часто
История вопроса об основополагающей теореме взятия отсчетов
Хотя в западной литературе теорема часто

Слайд 5Из теоремы Котельникова следует, что при дискретизации аналогового сигнала потерь информации не будет только в том
Из теоремы Котельникова следует, что при дискретизации аналогового сигнала потерь информации не будет только в том

Реальные сигналы конечной длительности всегда имеют бесконечно широкий спектр, более или менее быстро убывающий с ростом частоты. Поэтому дискретизация сигналов всегда приводит к потерям информации (искажению формы сигнала при дискретизации—восстановлении), как бы ни была высока частота дискретизации. При выбранной частоте дискретизации искажение можно уменьшить, если обеспечить подавление спектральных составляющих аналогового сигнала (до дискретизации), лежащих выше частоты Найквиста, для чего требуется противоподменный фильтр очень высокого порядка, чтобы избежать наложения «хвостов». Практическая реализация такого фильтра весьма сложна, так как амплитудно-частотные характеристики фильтров имеют не прямоугольную, а гладкую форму, и образуется некоторая переходная полоса частот между полосой пропускания и полосой подавления. Поэтому частоту дискретизации выбирают с запасом, к примеру, в аудио компакт-дисках используется частота дискретизации 44100 Герц, в то время как высшей частотой в спектре звуковых сигналов, которую может услышать человек, считается частота 20000 Гц. Запас по частоте Найквиста в 44100 / 2 - 20000 = 2050 Гц позволяет избежать подмены частот при использовании реализуемого фильтра невысокого порядка.
Слайд 6При доказательстве теоремы Котельникова взяты ограничения на спектр частот 0<ω<ω1, ω=2πf.
Такая трактовка
При доказательстве теоремы Котельникова взяты ограничения на спектр частот 0<ω<ω1, ω=2πf.
Такая трактовка

Разумеется, реальные сигналы (например, звук на цифровом носителе) не обладают такими свойствами, так как они конечны по времени и обычно имеют разрывы во временно́й характеристике. Соответственно, ширина их спектра бесконечна. В таком случае полное восстановление сигнала невозможно, и из теоремы Котельникова вытекают следствия:
любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчётам, взятым с частотой f>2fc, где fc — максимальная частота, которая ограничена спектром реального сигнала;
если максимальная частота в сигнале равна или превышает половину частоты дискретизации (наложение спектра), то способа восстановить сигнал из дискретного в аналоговый без искажений не существует.
Говоря шире, теорема Котельникова утверждает, что непрерывный сигнал x(t) можно представить в виде интерполяционного ряда:
Где sinc(x)=sin(x)/x функция синк. Интервал дискретизации удовлетворяет ограничениям 0<Δ<1/2fc. Мгновенные значения данного ряда есть дискретные отсчёты сигнала x(kΔ).
Слайд 7Элементы приемника данных (контроля моделируемой схемы
и вывода данных из точек анализа)
BeamMeasurement Part
BER
Элементы приемника данных (контроля моделируемой схемы
и вывода данных из точек анализа)
BeamMeasurement Part
BER

BER IS Part
CCDF Part
Constellation Part
DataPort Part
DigitalDemod Part
Dynamic3D Part
EVM Part
EyeDiagram Part
FlexDCA Sink Part
RMSE Part
SINAD Part
Sink Part
SpectrumAnalyzer Part
WriteBaseBandStudioFile Part
WriteFile Part
Слайд 8Приемник данных (универсальный вывод данных)
Description: Data Sink
Domain: Timed
C++ Code Generation Support: NO
SystemVueEngine Support: YES (ContinuousMode=YES не
Приемник данных (универсальный вывод данных)
Description: Data Sink Domain: Timed C++ Code Generation Support: NO SystemVueEngine Support: YES (ContinuousMode=YES не
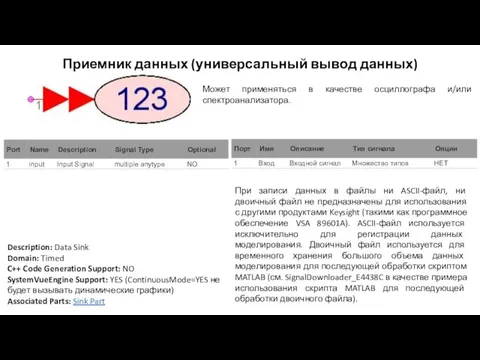
При записи данных в файлы ни ASCII-файл, ни двоичный файл не предназначены для использования с другими продуктами Keysight (такими как программное обеспечение VSA 89601A). ASCII-файл используется исключительно для регистрации данных моделирования. Двоичный файл используется для временного хранения большого объема данных моделирования для последующей обработки скриптом MATLAB (см. SignalDownloader_E4438C в качестве примера использования скрипта MATLAB для последующей обработки двоичного файла).
Может применяться в качестве осциллографа и/или спектроанализатора.
Слайд 10Анализаторы спектра. Общие сведения
По диапазону частот — низкочастотные, радиодиапазона (широкополосные) и оптического диапазона.
По
Анализаторы спектра. Общие сведения
По диапазону частот — низкочастотные, радиодиапазона (широкополосные) и оптического диапазона.
По

По способу обработки измерительной информации и представлению результатов — аналоговые и цифровые.
По характеру анализа — скалярные, дающие информацию только об амплитудах гармонических составляющих спектра, и векторные, предоставляющие также информацию о фазовых соотношениях.
Основные свойства анализа
Анализатор спектра позволяет определить амплитуду и частоту спектральных компонентов, входящих в состав анализируемого процесса. Важнейшей его характеристикой является разрешающая способность: наименьший интервал Δf по частоте между двумя спектральными линиями, которые ещё разделяются анализатором спектра. Анализатор спектра может дать истинный спектр только тогда, когда анализируемое колебание x(t) периодично, либо существует только в пределах интервала T. При анализе длительностей процессов анализатор спектра даёт не истинный спектр
а его оценку , зависящую от времени включения t1 и времени анализа Т. ак как спектр колебания может в общем случае изменяться во времени, то оценка даёт т. н. текущий спектр.
Слайд 11Низкочастотные анализаторы
НЧ анализаторы бывают параллельного и последовательного типа (чаще параллельного) и предназначены
Низкочастотные анализаторы
НЧ анализаторы бывают параллельного и последовательного типа (чаще параллельного) и предназначены

ПРИМЕРЫ: UPV, UPP, Ф4327, С4-34, СК4-83, ZET017, FLUKE_41B (анализатор гармоник), ZET 017.
Радиочастотные анализаторы
Большинство радиочастотных анализаторов являются широкополосными, позволяют работать в полосе от нескольких килогерц до единиц — сотен гигагерц, как правило, это анализаторы последовательного типа. Применяются для анализа свойств радиосигналов, для исследования характеристик радиоустройств.
ПРИМЕРЫ: FSL, FSV, FSU, СК4-84, С4-82, GSP-810
Анализаторы последовательного типа
Анализаторы последовательного типа являются наиболее распространенным видом анализаторов для исследования радиосигналов, принцип их действия состоит в сканировании полосы частот с помощью перестраиваемого гетеродина. Составляющие спектра последовательно переносятся на промежуточную частоту. Перестройка частоты гетеродина эквивалентна перемещению спектра исследуемого сигнала. Селективный УПЧ последовательно выделяет составляющие спектра, и, благодаря синхронной развёртке осциллографического индикатора, отклики каждой спектральной составляющей последовательно воспроизводятся на его экране.
Слайд 12Анализаторы параллельного типа
Анализаторы параллельного типа содержат набор идентичных узкополосных фильтров (высокодобротных резонаторов), каждый
Анализаторы параллельного типа
Анализаторы параллельного типа содержат набор идентичных узкополосных фильтров (высокодобротных резонаторов), каждый

Цифровые анализаторы
Цифровые анализаторы могут быть построены двумя способами. В первом случае это обычный анализатор последовательного типа, в котором измерительная информация, полученная методом сканирования полосы частот с помощью гетеродина, оцифровывается с помощью АЦП и, далее, обрабатывается цифровым методом. Во втором случае реализуется цифровой эквивалент параллельного типа в виде ДПФ-анализатора, который вычисляет спектр с помощью алгоритмов дискретного преобразования Фурье (ДПФ). По сравнению с последовательными цифровые параллельные ДПФ-анализаторы обладают определёнными преимуществами: более высоким разрешением и скоростью работы, возможностью анализа импульсных и однократных сигналов. Они способны вычислять не только амплитудный, но и фазовый спектры, а также одновременно представлять сигналы во временной и частотной областях. К сожалению, параллельные ДПФ-анализаторы из-за ограниченных возможностей аналого-цифровых преобразователей (АЦП) работают только на относительно низких частотах.
Корпорация Tektronix создала цифровые анализаторы спектра реального времени. Они позволяют отслеживать в реальном масштабе времени быстрые изменения спектра, которые используются в некоторых видах современных коммуникационных систем. При этом, наряду с обычными спектрами, приборы позволяют строить спектрограммы, которые представляют собой множество спектров, представленных в различные моменты времени.
Слайд 13Анализатор спектра комплексной огибающей сигналов
Модель анализатора спектра может быть использована для измерения
Анализатор спектра комплексной огибающей сигналов
Модель анализатора спектра может быть использована для измерения

Слайд 14Примечания к анализатору комплексной огибающей сигнала
Анализатор спектра имеет два режима работы: Time
Примечания к анализатору комплексной огибающей сигнала
Анализатор спектра имеет два режима работы: Time

Спектр сигнала основной полосы частот простирается от 0 Гц до 1/(2 × TStep) Гц. Спектр радиочастотного сигнала простирается от fc − 1/(2 × TStep) Гц до fc + 1/(2 × TStep) Гц. Когда fc < 1/(2 × TStep), спектр расширяется до отрицательных частот. Спектральное содержание на этих отрицательных частотах комплексно сопряжено, отзеркалено и добавлено к содержимому спектра ближайшей положительной частоты. Таким образом, отрицательные частотные гармоники отображаются на положительной частотной оси, как это происходит в реальном измерительном приборе анализатора спектра. Этот процесс может привести к ошибке в отображаемой частоте для зеркальных гармоник. При этом абсолютная ошибка меньше Δf/2, где Δf равно 1/SegmentTime (в режиме TimeGate) и ResBW/NENBW (в режиме ResBW).
Слайд 15Примечания к анализатору комплексной огибающей сигнала
При обработке и усреднении нескольких сегментов усреднение
Примечания к анализатору комплексной огибающей сигнала
При обработке и усреднении нескольких сегментов усреднение

Слайд 16Оконная обработка
Оконные окна необходимы при оценке спектра на основе преобразования (БПФ). Без
Оконная обработка
Оконные окна необходимы при оценке спектра на основе преобразования (БПФ). Без

Слайд 17Рекомендации по применению типов окон
Не используйте окно (установите окно на Равномерное) при
Рекомендации по применению типов окон
Не используйте окно (установите окно на Равномерное) при

Для периодических сигналов, спектральные компоненты которых имеют сравнимую амплитуду и когда обрабатываемый сегмент сигнала включает точное целое число, кратное периодам, наилучшие результаты получаются, если не используется окно (установить окно на Uniform). Любые переходные процессы запуска должны быть исключены.
Для периодических сигналов, спектральные компоненты которых имеют значительно различающиеся амплитуды и/или когда обрабатываемый сегмент сигнала не включает точное целое число, кратное периодам, использование окна может улучшить обнаружение более слабых спектральных компонентов. Чем выше NENBW, тем более вероятно, что будут обнаружены более слабые спектральные компоненты. Однако это меняет частотное разрешение, и поэтому, если спектральные компоненты находятся очень близко друг к другу, более слабая из них может остаться неразрешенной. Для улучшения частотного разрешения при сохранении хорошего динамического диапазона используйте окно, но обрабатывайте более длинный сегмент сигнала.
Для апериодических сигналов, таких как модулированные сигналы (QPSK, QAM, GSM, EDGE, CDMA, OFDM), настоятельно рекомендуется использовать окно. Окно ослабит сигнал на обоих концах обрабатываемого сегмента сигнала до нуля. Это делает сигнал квазипериодическим и уменьшает ошибки при измерениях.
Слайд 18Аналитические выражения для весовых функций (окон)
Когда сигнал временной области обрабатывается окном, отличным
Аналитические выражения для весовых функций (окон)
Когда сигнал временной области обрабатывается окном, отличным

Слайд 19Параметр Persistence можно использовать для уменьшения размера файла рабочей области, не сохраняя
Параметр Persistence можно использовать для уменьшения размера файла рабочей области, не сохраняя

Слайд 21Запись данных моделирования в файл
Запись данных моделирования в файл
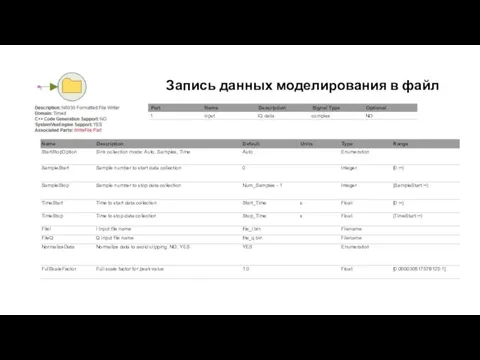
Слайд 22Опции компонента записи в файл
Данная модель записывает реальную и мнимую части комплексных
Опции компонента записи в файл
Данная модель записывает реальную и мнимую части комплексных

IQ данные представляются в виде комплексного значения со значением I в действительной части и значением Q в мнимой части.
Параметр Start Stop Option указывает режим сбора данных:
если установлено значение Samples, то сбор данных будет начинаться с отсчета Sample Start и останавливаться на SampleStop;
если установлено значение Time, сбор данных начнется в момент времени Time Start и остановится в момент времени TimeStop;
если установлено значение авто, то все параметры SampleStart, SampleStop, TimeStart, и TimeStop должны быть заранее определены и симулятор сам будет выбирать в реальном времени что использовать: SampleStart/SampleStop или TimeStart/TimeStop. Решение основано на том, имеет ли входной сигнал заданную частоту дискретизации. Если частота дискретизации не определена (например, сигнал сгенерирован SineGen с параметром частоты дискретизации SampleRateOption, установленным в UnTimed), то используется SampleStart/SampleStop. В противном случае используется TimeStart/TimeStop.
Параметры FileI и FileQ используются для определения выходных файлов для данных I и Q. Файлы могут быть указаны с полным или относительным именем пути. Относительные имена путей относятся к каталогу, в котором находится проект.
Параметр Normalize Data определяет, будут ли данные обрезаны или нормализованы перед их записью в файлы:
если установлено значение NO (НЕТ), нормализация не выполняется. Значения данных за пределами диапазона [-FullScaleFactor, FullScaleFactor] вырезаются в пределах этого диапазона. Кроме того, отображается предупреждающее сообщение, информирующее пользователя о том, что произошла обрезка данных;
если установлено значение ДА, отсечение не выполняется, и данные, записанные в файлы, являются масштабированной (нормализованной) версией входных данных, так что они всегда находятся в диапазоне [-FullScaleFactor, FullScaleFactor]. Используемый коэффициент масштабирования отображается в информационном сообщении в окне Errors, а также в лог-файле моделирования.
Слайд 23Формат N6030 записи данных в файл
N6030 считывает данные I и Q из
Формат N6030 записи данных в файл
N6030 считывает данные I и Q из

Слайд 24Динамические графики
Окно Dynamic Graphs (Динамических графиков) относится к отдельному окну, которое автоматически
Динамические графики
Окно Dynamic Graphs (Динамических графиков) относится к отдельному окну, которое автоматически

Слайд 26Компонент оценок величины вектора ошибок измерений
Эта модель используется для выполнения измерения EVM
Компонент оценок величины вектора ошибок измерений
Эта модель используется для выполнения измерения EVM

Определяющие уравнения для измерения EVM следуют определению в стандарте совместимости двухрежимной мобильной станции и базовой станции сотовой системы EIA/TIA IS-54-B TDMA, раздел 2.1.3.3.1.3.3 (Требование к величине вектора ошибки). Пусть Z(n) обозначает действительные комплексные векторы (I и Q), полученные наблюдением реального передатчика через идеальный фильтр приемника в моменты времени n с интервалом в один символ. S(n) определяется как идеальный эталонный символ (нормированный таким образом, чтобы его максимальный энергетический символ приходился на единичную окружность). Тогда Z(n) моделируется как:
Где учитывает как частоту смещения (Da radians/symbol phase rotation), так и скорость изменения амплитуды (Dr nepers/symbol)
С0 - является комплексным постоянным смещением начала координат (в вольтах)
С1 - является безразмерной комплексной константой, представляющей произвольную фазу и выходную мощность передатчика
E(n) - является вектором остаточной ошибки по выборке S(n)
Слайд 27Сумма квадратов вектора ошибок равна:
где N равно ResultLength и C0, C1, W
Сумма квадратов вектора ошибок равна:
где N равно ResultLength и C0, C1, W
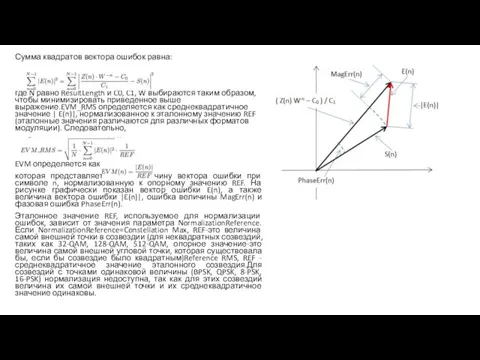
EVM определяется как
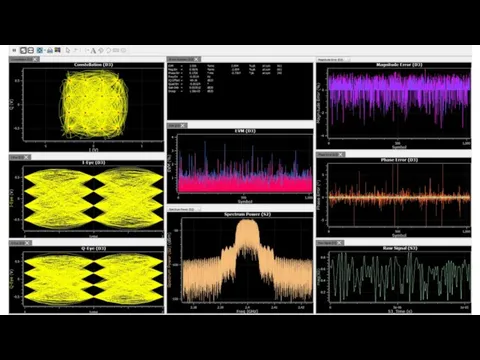
которая представляет собой величину вектора ошибки при символе n, нормализованную к опорному значению REF. На рисунке графически показан вектор ошибки E(n), а также величина вектора ошибки |E(n)|, ошибка величины MagErr(n) и фазовая ошибка PhaseErr(n).
Эталонное значение REF, используемое для нормализации ошибок, зависит от значения параметра NormalizationReference. Если NormalizationReference=Constellation Max, REF-это величина самой внешней точки в созвездии (для неквадратных созвездий, таких как 32-QAM, 128-QAM, 512-QAM, опорное значение-это величина самой внешней угловой точки, которая существовала бы, если бы созвездие было квадратным)Reference RMS, REF - среднеквадратичное значение эталонного созвездия.Для созвездий с точками одинаковой величины (BPSK, QPSK, 8-PSK, 16-PSK) нормализация недоступна, так как для этих созвездий величина их самой внешней точки и их среднеквадратичное значение одинаковы.
Слайд 28Параметр Start задает время начала сбора данных. Убедитесь, что вы установили Start,
Параметр Start задает время начала сбора данных. Убедитесь, что вы установили Start,

Для обеспечения возможности установки внутренних фильтров модель будет собирать образцы данных еще до запуска, так что фактическое измерение начнется как можно ближе к началу. Если перед запуском не хватает образцов данных, то Запуск сбрасывается на более высокие значения и отображается предупреждение.
Параметр SymbolRate задает частоту символов, с которой будет выполняться измерение, и должен соответствовать частоте символов входного сигнала.
Параметр ResultLength задает количество символов, по которым будет выполняться измерение.
Параметр ModType выбирает формат модуляции, для которого будет выполняться измерение, и должен соответствовать формату входного сигнала. Для некоторых параметров ModType необходимо установить дополнительные параметры.
Параметр UserDefinedConstellation указывает точки созвездия, когда ModType определяется пользователем.
Параметры Ratio_R2_R1, Ratio_R3_R1 и Ratio_R4_R1 используются для установки отношения второй, третьей и четвертой кольцевых величин к первой кольцевой величине для форматов 16-APSK, 32-APSK, Star 16-QAM и Star 32-QAM.
Ratio_R2_R1 применим для 16-АПСК, 32-АПСК звезды 16-QAM и звезда 32-Кам.
Ratio_R3_R1 применимо к 32-APSK и Star 32-QAM.Ratio_R4_R1 применимы только к Star 32-QAM.
Параметры RingStates, Ringmagnitudes и RingInitialPhase используются для определения пользовательских созвездий APSK, где точки созвездий равномерно распределены вокруг коцентрических колец. Более подробную информацию о созвездиях для поддерживаемых форматов модуляции см. в разделе DigitalMod.
Слайд 29Параметры MeasurementFilter и ReferenceFilter определяют, какая фильтрация будет выполняться на входе и
Параметры MeasurementFilter и ReferenceFilter определяют, какая фильтрация будет выполняться на входе и

Длина встроенных измерительных и эталонных фильтров составляет 15 символов. Если для любого из фильтров выбран вид характеристики Root Raised Cosine или Raised Cosine, то параметр Alpha устанавливает их точку среза. Для правильной настройки измерения EVM фильтр формирования импульсов, используемый при генерации сигнала в передатчике TX, каскадируемый измерительным фильтром, должен привести к эталонному фильтру. Измерительный фильтр может быть реализован вне модели EVM (если требуется точное управление параметрами фильтра, например длиной фильтра, точностью фиксированной точки и т. Д.), и в этом случае параметр MeasurementFilter должен быть установлен в значение None. В следующей таблице приведены некоторые примеры правильных настроек (Измерительный фильтр-это либо встроенный измерительный фильтр EVM, определенный в параметре MeasurementFilter, либо внешний фильтр).
Слайд 30Модель EVM работает с сигналами, которые представляют собой ОДНУ модулированную несущую. Когда
Модель EVM работает с сигналами, которые представляют собой ОДНУ модулированную несущую. Когда

Слайд 31Результаты измерений, сохраненные в наборе данных, описаны ниже.
EVM_RMS: Значение EVM_RMS, выражается
Результаты измерений, сохраненные в наборе данных, описаны ниже.
EVM_RMS: Значение EVM_RMS, выражается

EVM_Peak: максимальное значение символа EVM, max {EVM(n)} n = 0, 1, ..., N-1, выраженное в %.
EVM_PeakSymbolIndex: индекс символа, в котором произошел выброс EVM_Peak.
MagErrorRMS: Среднеквадратичное значение ошибки величины символа (MagErr(n)), нормализованное по опорному уровню REF и выраженное в %.
MagErrorPeak: максимальное значение символа с выбросом данных (превышением пикового уровня) MagErr, max {MagErr(n)} n = 0, 1, ..., N-1, выраженное в %.
MagErrorPeakSymbolIndex: индекс символа, в котором произошел выброс MagErrorPeak.
PhaseErrorRMS: среднеквадратичное значение ошибки фазы символа (PhaseErr(n)).
PhaseErrorPeak: максимальное значение символа PhaseErr, max {PhaseErr(n)} n = 0, 1, ..., N-1.
PhaseErrorPeakSymbolIndex: индекс символа, в котором произошел PhaseErrorPeak.
FreqError: частотная ошибка, (SymbolRate * Da / ( 2 * π)).
IQ_Offset: смещение IQ, значение постоянного уровня сигнала несущей; |C0| нормализовано REF и выражено в дБ; 20 * log10(|C0|/REF).
Quad Err: квадратурная ошибка перекоса (также называемая фазовым дисбалансом), мера ортогональности сигналов I и Q, выраженная в градусах.
GainImbalance: дисбаланс усиления, мера разницы в усилении сигналов I и Q, выраженная в дБ.
Droop: выражается в дБ; -20 * log10(eDr).
SNR: отношение сигнал / шум выражается в децибелах.
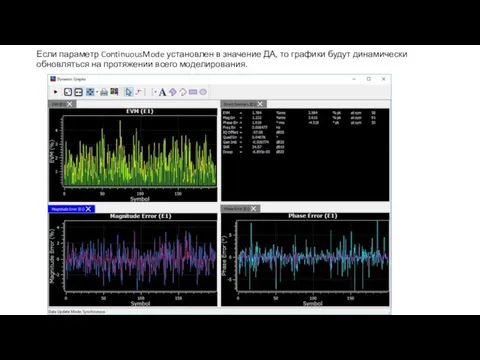
Слайд 32Если параметр ContinuousMode установлен в значение ДА, то графики будут динамически обновляться
Если параметр ContinuousMode установлен в значение ДА, то графики будут динамически обновляться
Слайд 33Глазковая диаграмма
Эта модель создает динамический график, отображающий глазковую диаграмму входного сигнала.
Параметр SymbolRate
Глазковая диаграмма
Эта модель создает динамический график, отображающий глазковую диаграмму входного сигнала.
Параметр SymbolRate

Параметр Offset можно использовать для смещения диаграммы вдоль нижней оси графика так, чтобы вы могли центрировать ее в середине графика. Этот параметр настраивается во время выполнения (настраивается во время моделирования), поэтому нет необходимости знать оптимальное значение до начала моделирования. Допустимый диапазон смещения - [0, N-1]. Если во время настройки присваивается значение, выходящее за пределы этого диапазона, то значение обрезается до пределов этого диапазона. В общей сложности символы результирующей длины показаны на диаграмме. Каждый след имеет длину 2 символа, поэтому общее количество следов равно N / 2. Эта модель НЕ делает никакой демодуляции. Входной сигнал уже должен быть демодулирован с целым числом отсчетов на символ. Эта модель НЕ делает никакой интерполяции. Поэтому даже для идеального или близкого к идеальному сигнала, если входной сигнал не включает выборку в оптимальный момент выборки (например, из-за частичных задержек выборки, вносимых фильтрами), вы не сможете получить "чистую" диаграмму с "идеальным" открытием.
Глазковая диаграмма представляет собой “осциллограмму” аналогового демодулированного сигнала, построенную при длительности “прямого хода развертки”, равной одному символьному такту, и бесконечном “времени послесвечения экрана”. В точках оптимальной дискретизации линии на такой диаграмме образуют узкие пучки, свободное пространство между которыми по форме напоминает раскрытый глаз.
Слайд 34Основы глазковой диаграммы: чтение и применение глазковых диаграмм
Увеличение скоростей передачи данных, бо́льшая
Основы глазковой диаграммы: чтение и применение глазковых диаграмм
Увеличение скоростей передачи данных, бо́льшая

При передаче от передатчика к приемнику последовательный цифровой сигнал может ухудшаться. Передатчик, дорожки печатной платы, разъемы и кабели будут создавать помехи, которые ухудшают сигнал, как по амплитуде, так и по времени. Сигнал также может пострадать от внутренних источников. Например, когда сигналы на соседних парах трасс печатной платы или на выводах микросхемы переключаются, перекрестные связи между этими сигналами могут создавать помехи другим сигналам. Таким образом, вам нужно определить, в какую точку поместить щуп осциллографа, чтобы получить глазковую диаграмму, которая поможет вам определить источник проблемы. Кроме того, в зависимости от того, куда вы поместите щуп осциллографа, сигналы на экране будут различаться.
Слайд 35Получение глазковой диаграммы
Глазковая диаграмма – это распространенный индикатор качества сигналов в высокоскоростных
Получение глазковой диаграммы
Глазковая диаграмма – это распространенный индикатор качества сигналов в высокоскоростных

В идеальном мире глазковые диаграммы выглядят как прямоугольные коробки. В реальности, каналы связи не идеальны, поэтому переходы не идеально выровнены друг с другом, и в результате получается рисунок в форме глаза. Форма глазковой диаграммы на осциллографе будет зависеть от различных типов сигналов запуска, таких как сигнал запуска с тактовой частотой потока, сигнал запуска с деленной тактовой частотой потока, запуск по кодовой комбинации (pattern trigger). Различия по времени и амплитуде от бита к биту приводят к уменьшению открытия глаза.
Слайд 36Интерпретация глазковой диаграммы
Правильно построенный глаз должен содержать каждую возможную битовую последовательность от
Интерпретация глазковой диаграммы
Правильно построенный глаз должен содержать каждую возможную битовую последовательность от

Идеальная глазковая диаграмма содержит огромное количество параметрической информации о сигнале, подобно эффектам, вытекающим из физики, независимо от того, как эти эффекты возникают. Если логическая 1 настолько искажена, что приемник на дальнем конце может неверно принять ее за логический 0, вы легко заметите это по глазковой диаграмме. Однако по ней вы не сможете обнаружить проблемы логики или протокола, например, когда система должна передавать логический 0, но отправляет логическую 1, или когда логика конфликтует с протоколом.
Слайд 37Джиттер
Хотя теоретически глазковые диаграммы должны выглядеть как прямоугольные коробки, конечное время нарастания
Джиттер
Хотя теоретически глазковые диаграммы должны выглядеть как прямоугольные коробки, конечное время нарастания

Джиттер возникает, когда нарастающие и спадающие фронты происходят в моменты, отличные от идеального времени. Некоторые фронты появляются рано, некоторые – поздно. В цифровой схеме все сигналы передаются относительно тактовых сигналов. Отклонение цифровых сигналов в результате отражений, межсимвольных помех, перекрестных помех, влияний изменений напряжения и температуры и других факторов приводит к джиттеру. Некоторый джиттер будет просто случайным.
На рисунке c абсолютная ошибка по времени или поле фазового дрожания меньше, чем на рисунке b, но открытие глаза на рисунке c меньше из-за более высокой скорости передачи данных. С увеличением скорости передачи данных абсолютная ошибка по времени представляет собой увеличивающуюся часть периода сигнала, таким образом, уменьшая размер открытия глаза. Это может увеличить вероятность ошибок в данных.
Слайд 38На сгенерированных глазковых диаграммах хорошо виден эффект разрыва. При неправильной нагрузке конца
На сгенерированных глазковых диаграммах хорошо виден эффект разрыва. При неправильной нагрузке конца

(a) Неправильная нагрузка заставляет глазковую диаграмму выглядеть «напряженной» (сдавленной).
(b) Правильная нагрузка «расслабляет» глаз.
Слайд 39Как видно на рисунке, глазковая диаграмма может показать важную информацию. Она может
Как видно на рисунке, глазковая диаграмма может показать важную информацию. Она может

Глазковая диаграмма может помочь вам интерпретировать сигнал и определить наилучшее время для измерений.
Слайд 40CCDF_Cx
Модель CCDF_Cx вычисляет комплементарную кумулятивную функцию распределения (CCDF) сложного сигнала.
Расчет CCDF
CCDF_Cx
Модель CCDF_Cx вычисляет комплементарную кумулятивную функцию распределения (CCDF) сложного сигнала.
Расчет CCDF

Вычислите среднеквадратичное значение для всех измеренных выборок; оно становится точкой 0 дБ на оси x.
Нормализуйте все выборки до среднеквадратичного значения в единицах дБ.
Разделите ось x на равные по ширине ячейки NumBin, начиная с минимальной измеренной мощности и заканчивая максимальной измеренной мощностью.
Определите, к какой ячейке по оси x принадлежит каждый отсчет.
Вычислите общее количество выборок, и выведите его в процентах от числа измеренных выборок.
В дополнение к измерению CCDF эта модель может обеспечить пиковую мощность (пиковую мощность входного сигнала; это НЕ абсолютный пик, а 99,9-й процентиль) и среднюю мощность (среднюю или среднюю мощность входного сигнала). Чтобы вычислить и вывести MeanPower и PeakPower, установите для параметра OutputPeakMean значение YES.
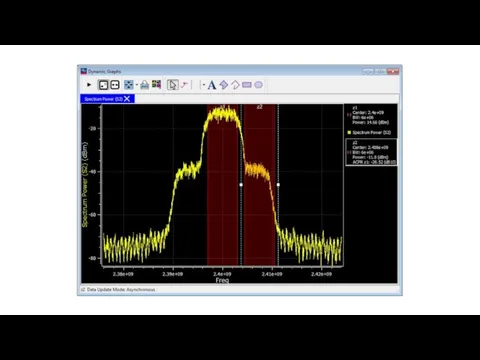
Измерение CCDF-это очень распространенное измерение, выполняемое на беспроводных сигналах 2G, 3G и 4G. Кривая CCDF показывает вероятность того, что мгновенная мощность сигнала будет выше средней мощности сигнала на определенную величину дБ. Независимая ось кривой CCDF показывает уровни мощности в дБ по отношению к среднему уровню мощности сигнала (0 дБ соответствует среднему уровню мощности сигнала). Зависимая ось кривой CCDF показывает вероятность того, что мгновенная мощность сигнала превысит соответствующий уровень мощности на независимой оси. На следующем рисунке показана кривая CCDF для нисходящего сигнала WiMAX 802.16 e. На рисунке видно, что мгновенная мощность сигнала превышает среднюю мощность сигнала (0 дБ) на 35% времени. Вы также можете видеть, что мгновенная мощность сигнала превышает среднюю мощность сигнала на 5 дБ только в 7% случаев.

 Презентация на тему Основоположники физики
Презентация на тему Основоположники физики  Резонанс механических колебаний
Резонанс механических колебаний Механические волны
Механические волны Радиоволны. История открітия
Радиоволны. История открітия Постоянные магниты. Магнитное поле
Постоянные магниты. Магнитное поле Оптика и квантовая физика. Лекция 12
Оптика и квантовая физика. Лекция 12 Электрический ток. Сила тока. Закон Ома. Сопротивление
Электрический ток. Сила тока. Закон Ома. Сопротивление Безопасность дорожного движения и особенности управления грузовым автомобилем
Безопасность дорожного движения и особенности управления грузовым автомобилем Момент импульса. Закон сохранения момента импульса
Момент импульса. Закон сохранения момента импульса Давление твердых тел, жидкостей и газов
Давление твердых тел, жидкостей и газов Нанокомпозиты: термодинамическое описание и размерные эффекты
Нанокомпозиты: термодинамическое описание и размерные эффекты Устройства ввода информации
Устройства ввода информации Давление газа
Давление газа Основное уравнение МКТ
Основное уравнение МКТ 一、选择题
一、选择题 Определение параметров колебательного движения
Определение параметров колебательного движения Сообщающиеся сосуды
Сообщающиеся сосуды Технологии ВВЭР
Технологии ВВЭР Строение и структура материалов
Строение и структура материалов Основные понятия кинематики. Простейшие движения твердого тела
Основные понятия кинематики. Простейшие движения твердого тела История развития радио. Радиоквиз
История развития радио. Радиоквиз Изучение последовательного и параллельного соединения проводников. Лабораторная работа
Изучение последовательного и параллельного соединения проводников. Лабораторная работа Изображения, даваемые линзой
Изображения, даваемые линзой Экспериментальная ядерная физика
Экспериментальная ядерная физика Источники звука. Звуковые колебания
Источники звука. Звуковые колебания Криволинейное движение. Центростремительное (нормальное) ускорение
Криволинейное движение. Центростремительное (нормальное) ускорение Презентация по физике _Ускорение. 9 класс_
Презентация по физике _Ускорение. 9 класс_ Механические передачи и их применение
Механические передачи и их применение