Слайд 3Instantaneous Basin loss at a Fold
Before After

Слайд 4Introduction
Focus on the Earth, or a relevant sub-system (Lenton).
Regard it as a

nonlinear dissipative dynamical system.
Ignore discontinuities and memory effects.
We have a large but finite set of ODEs and phase space.
This large complex system has activity at many scales.
Слайд 5Effective Noise
Small fast action is noise to the overall dynamics (OD)
Models

of the OD might need added random noise
Bifurcations of the OD may underlie climate tipping
…………………………………………………..………………………….
Control Parameters
We may have many slowly-varying control parameters, µi
But they can subsumed into a single µ (eg. slow time)
This limits the relevant bifurcations to those with co-dimension (CD) = 1
We now explain the co-dimension concept, before moving on to classify the CD = 1 bifurcations
Слайд 6Unfolding Euler’s Pitchfork
A real column has imperfections.
With P it does not reach
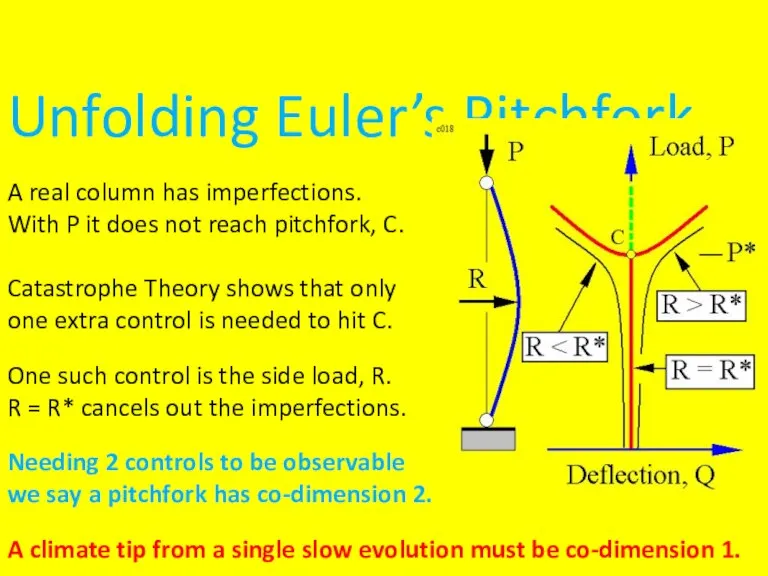
pitchfork, C.
Catastrophe Theory shows that only
one extra control is needed to hit C.
One such control is the side load, R.
R = R* cancels out the imperfections.
Needing 2 controls to be observable
we say a pitchfork has co-dimension 2.
A climate tip from a single slow evolution must be co-dimension 1.
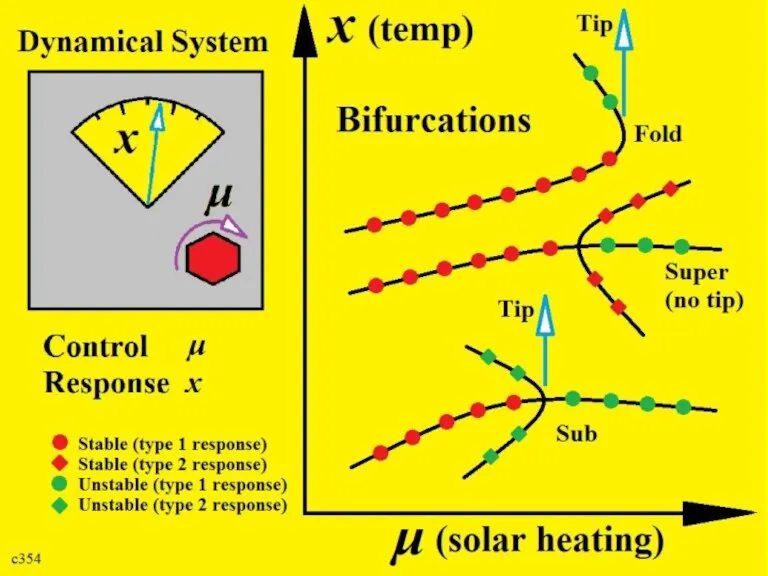
Слайд 7Co-Dimension 1 Bifurcations
(we shall be listing all 18)
Bifurcations can be classified

as:
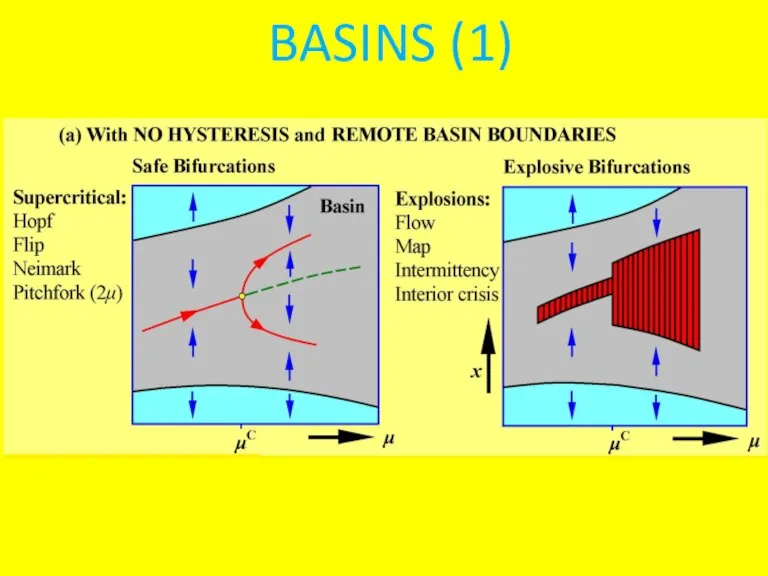
(a) Safe Bifurcations
(b) Explosive Bifurcations
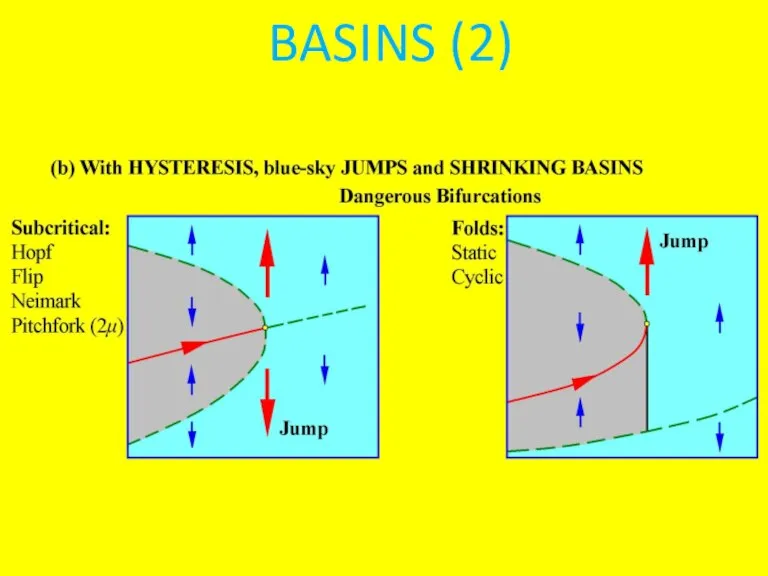
(c) Dangerous Bifurcations
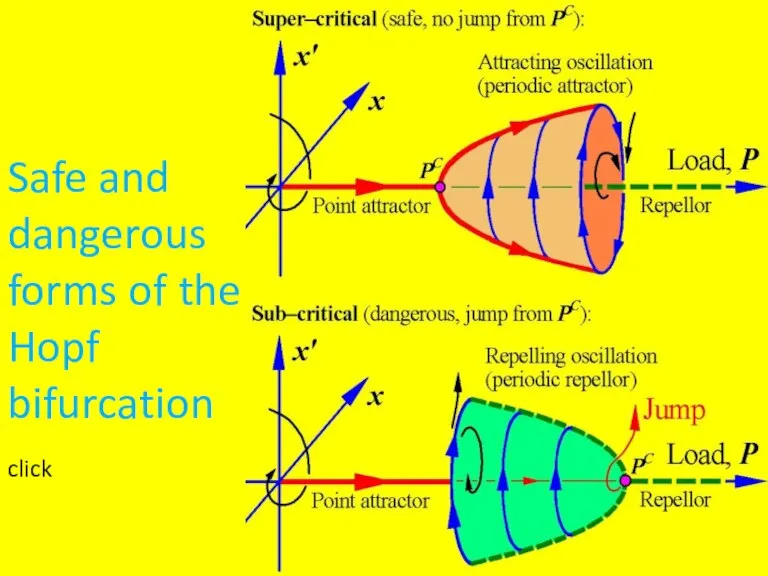
Слайд 8Safe and
dangerous
forms of the
Hopf
bifurcation
click
Слайд 11Example of an Explosive Event
Flow-explosion transforms point attractor to a cycle
Equilibrium path
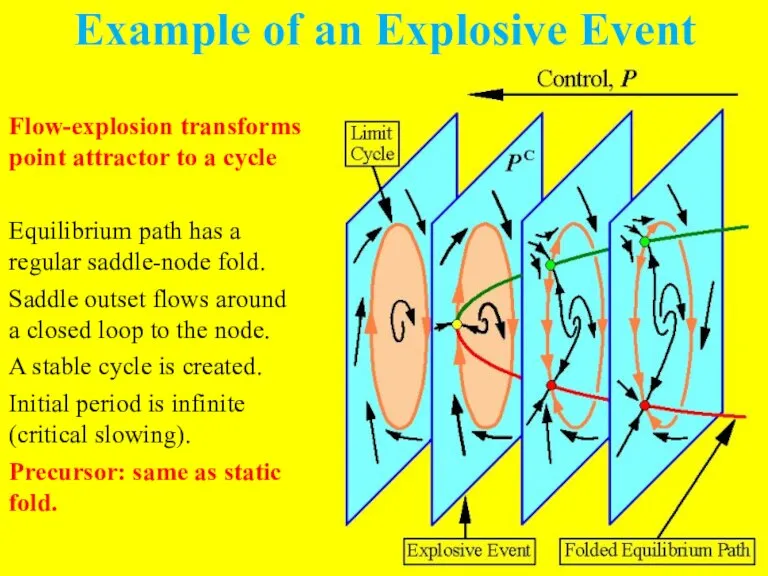
has a regular saddle-node fold.
Saddle outset flows around a closed loop to the node.
A stable cycle is created.
Initial period is infinite (critical slowing).
Precursor: same as static fold.
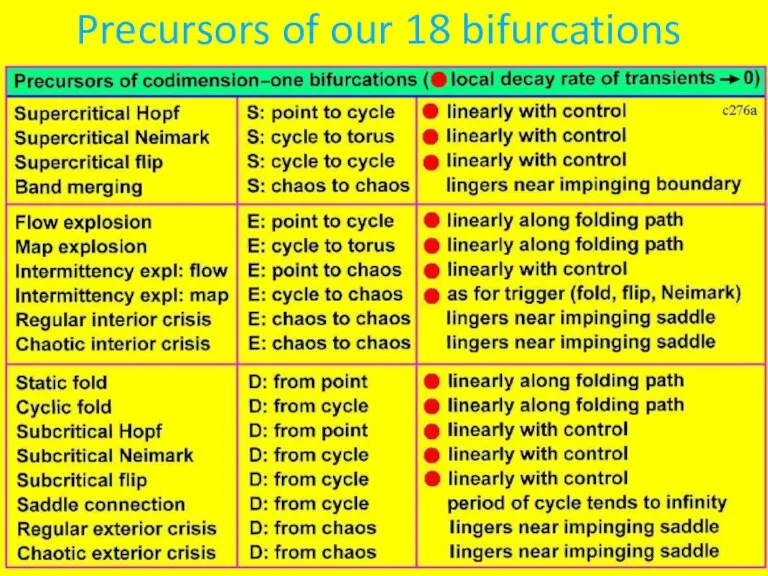
Слайд 15Precursors of our 18 bifurcations
Слайд 17Concluding Remarks
Bifurcation concepts for climate studies:
Co-dimension-one events in dissipative systems.
Safe, explosive and

dangerous forms.
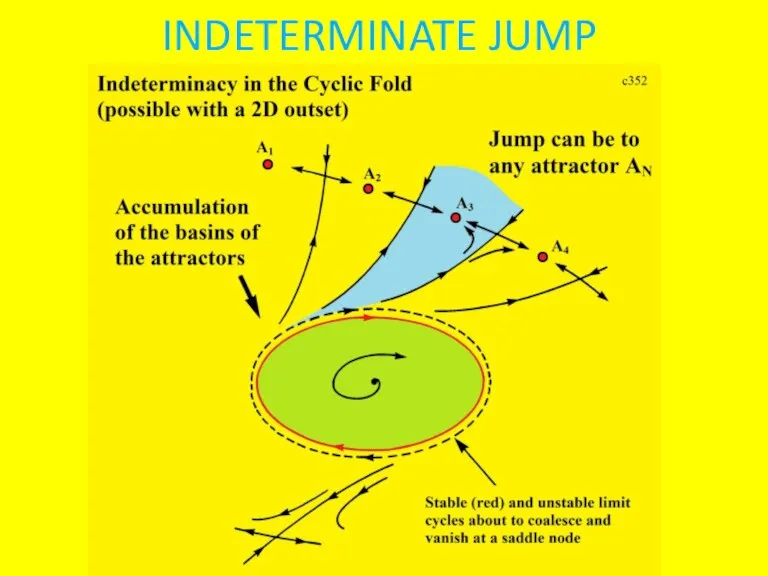
Hysteresis and basin boundary structure
Slowing of transients prior to an instability.












 Презентация на тему Степи России
Презентация на тему Степи России  20171221_vulkanygoryaie_istochniki_geyzery
20171221_vulkanygoryaie_istochniki_geyzery Китай (КНР)
Китай (КНР) Водные ресурсы мира
Водные ресурсы мира Низкоуровневые струйные течения надо льдом в Арктике: влияние неоднородностей подстилающей поверхности
Низкоуровневые струйные течения надо льдом в Арктике: влияние неоднородностей подстилающей поверхности Королевство Свазиленд
Королевство Свазиленд Современный облик планеты Земля. Тестовая работа
Современный облик планеты Земля. Тестовая работа США и Канада Подготовили студенты группы Т-1202 Сембина А., Бекенов К.
США и Канада Подготовили студенты группы Т-1202 Сембина А., Бекенов К. Что такое почва (3 класс)
Что такое почва (3 класс) Презентация на тему Замок Химэдзи
Презентация на тему Замок Химэдзи  20170124_zemlya_kak_planeta_solnechnoy_sistemy
20170124_zemlya_kak_planeta_solnechnoy_sistemy Mali azijski tigri
Mali azijski tigri Рельеф
Рельеф Canada
Canada Презентация на тему Земледелие
Презентация на тему Земледелие  Тюменская область
Тюменская область Презентация на тему Тюменской области 70 лет
Презентация на тему Тюменской области 70 лет  Презентация на тему Семь Вершин Мира
Презентация на тему Семь Вершин Мира  Население Оренбургской области. Национальный состав
Население Оренбургской области. Национальный состав Проверочная работа Страны мира
Проверочная работа Страны мира Экзогенные геологические процессы
Экзогенные геологические процессы Ұңғыны және қабатты гидродинамикалық зерттеу
Ұңғыны және қабатты гидродинамикалық зерттеу Время и календарь
Время и календарь Байкал
Байкал Район Чертаново
Район Чертаново Пособие для отработки навыков работы с картой. Подготовка к ЕГЭ
Пособие для отработки навыков работы с картой. Подготовка к ЕГЭ Populācija. Populāciju raksturojošie lielumi
Populācija. Populāciju raksturojošie lielumi Рекреалогия. Рекреационный потенциал региона
Рекреалогия. Рекреационный потенциал региона