8-1-1

Ключевые слова
система счисления
цифра
алфавит
позиционная система счисления
основание
развёрнутая форма записи числа
свёрнутая форма записи числа
двоичная система счисления
восьмеричная система счисления
шестнадцатеричная система счисления

Система счисления - это знаковая система, в которой приняты определённые правила записи чисел.
Цифры - знаки, при помощи которых записываются числа.
Алфавит системы счисления - совокупность цифр.
Общие сведения
Древнеславянская система счисления
Вавилонская система счисления
Египетская система счисления

Узловые числа обозначаются цифрами.
Узловые и алгоритмические числа
Алгоритмические числа получаются в результате каких-либо операций из узловых чисел.
× 100 +
× 10 +
=

Простейшая и самая древняя система - унарная система счисления. В ней для записи любых чисел используется всего один символ - палочка, узелок, зарубка, камушек.
Унарная система счисления
Узелковое письмо «кипу»
Зарубки
Примеры узлов «кипу»
Узелки, дощечки
Камушки

Римская система счисления
40
=
X
L
1935
M
C
M
X
X
X
28
X
X
V
I
I
I
V
Непозиционная система счисления
Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.
Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила:
каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.

Система счисления называется позиционной, если количественный эквивалент цифры в числе зависит от её положения в записи числа.
Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Позиционная система счисления

Цифры 1234567890 сложились в Индии около 400 г. н. э.
Арабы стали пользоваться подобной нумерацией около 800 г. н. э.
Примерно в 1200 г. н. э. эту нумерацию начали применять в Европе.
Десятичная система счисления

В позиционной системе счисления с основанием q любое число может быть представлено в виде:
Aq =±(an–1×qn–1+ an–2 × qn–2+…+ a0 × q0+ a–1×q–1+…+ a–m× q–m)
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Такая запись числа называется развёрнутой формой записи.
Основная формула

Aq =±(an–1 × qn–1+ an–2 × qn–2+…+ a0 × q0+ a–1 × q–1+…+ a–m × q–m)
Примеры записи чисел в развёрнутой форме:
2012=2×103 +0×102 +1×101 +2×100
0,125=1×10-1 +2×10-2 +5×10–3
14351,1=1×104 +4×103 +3×102 +5×101 +1×100 +1×10–1
Развёрнутая форма

Двоичная система счисления
Двоичной системой счисления называется позиционная система счисления с основанием 2.
Двоичный алфавит: 0 и 1.
Для целых двоичных чисел можно записать:
an–1an–2…a1a0 = an–1×2n–1 + an–2×2n–2 +…+ a0×20
Например:
100112 =1×24+0×23+0×22+1×21+1×20 = 24 +21 + 20 =1910
Правило перевода двоичных чисел в десятичную систему счисления:
Вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа

Правило перевода целых десятичных чисел в двоичную систему счисления
an–1×2n–1+an–2×2n–2+… a1×21 +a0
= an–1×2n–2 +…+ a1 (остаток a0)
2
an–1×2n–1+an–2×2n–2+… a1
= an–1×2n–3+…+ a2 (остаток a1)
2
. . .
an–1×2n–1+an–2×2n–2+… a2
= an–1×2n–4 +…+ a3 (остаток a2)
2
На n-м шаге получим набор цифр: a0a1a2…an–1

36310 = 1011010112
31410 = 1001110102
Компактное оформление

an–1an–2…a1a0 = an–1×8n–1+an–2×8n–2+…+a0×80
Пример: 10638 =1×83 +0×82+6×81+3×80=56310.
Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Восьмеричная система счисления
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю.
Восьмеричной системой счисления называется позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.

Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Шестнадцатеричная система счисления
Переведём десятичное число 154 в шестнадцатеричную систему счисления:
15410 = 9А16
154
16
9
-144
10
(А)
9
16
0
3АF16 =3×162+10×161+15×160 =768+160+15=94310.

1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
Цифровые весы
Правило перевода целых десятичных чисел в систему счисления с основанием q

Таблица соответствия 10-х, 2-х, 8-х и 16-х чисел от 1 до 16

Двоичная арифметика
Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения:
Арифметика одноразрядных двоичных чисел
Арифметика многоразрядных двоичных чисел
Умножение и деление двоичных чисел

«Компьютерные» системы счисления
Двоичная система используется в компьютерной технике, так как:
двоичные числа представляются в компьютере с помощью простых технических элементов с двумя устойчивыми состояниями;
представление информации посредством только двух состояний надёжно и помехоустойчиво;
двоичная арифметика наиболее проста;
существует математический аппарат, обеспечивающий логические преобразования двоичных данных.
Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и однородными кодами. Специалисты заменяют двоичные коды на величины в восьмеричной или шестнадцатеричной системах счисления.

Система счисления — это знаковая система, в которой приняты определённые правила записи чисел.
Система счисления называется позиционной, если количественный эквивалент цифры в числе зависит от её положения в записи числа.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
Aq =±(an–1×qn–1 + an–2×qn–2 +…+ a0×q0 + a–1×q–1 +…+ a–m×q–m)
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Самое главное

Вопросы и задания
Чем различаются унарные, позиционные и непозиционные системы счисления?
Цифры каких систем счисления приведены на рисунке?
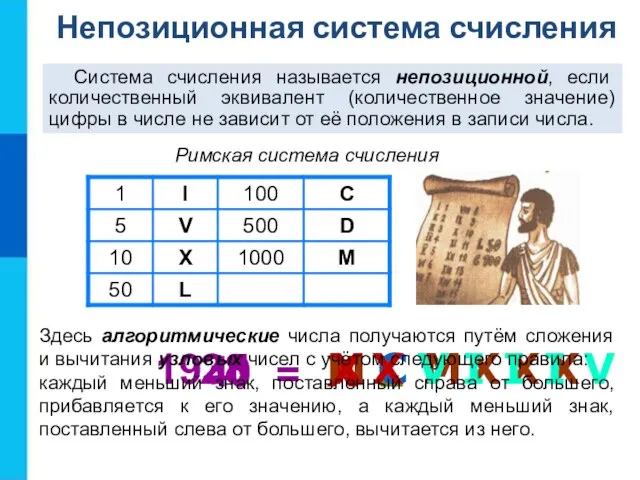
Объясните, почему позиционные системы счисления с основаниями 5, 10, 12 и 20 называют системами счисления анатомического происхождения.
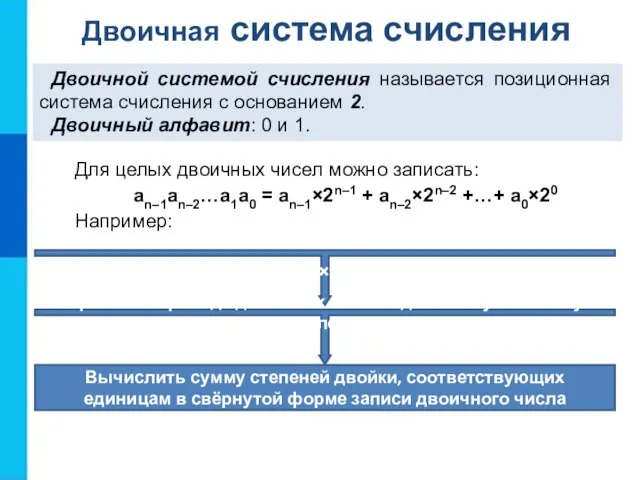
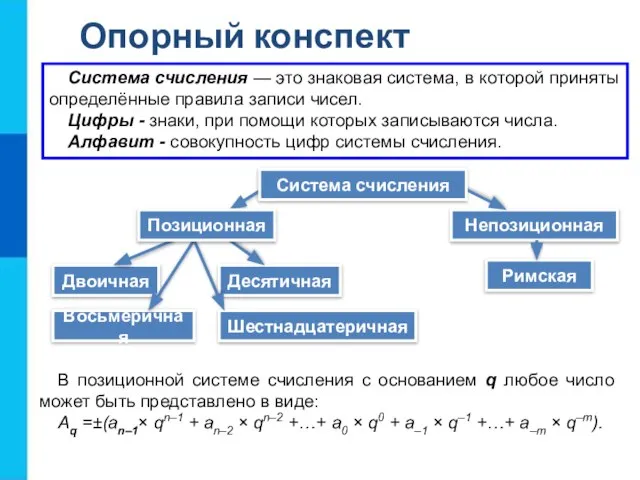
Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?
Запишите в развёрнутом виде числа:
а) 143,51110
б) 1435118
в) 14351116
г) 1435,118
Запишите десятичные эквиваленты следующих чисел:
а) 1728
б) 2ЕА16
в) 1010102
г) 10,12
д) 2436
Укажите, какое из чисел 1100112, 1114,358 и1В16 является:
а) наибольшим
б) наименьшим
Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите десятичный эквивалент данных чисел в найденной системе счисления.
Верны ли следующие равенства?
а) 334 =217
б) 338 =214
Найдите основание х системы счисления, если:
а) 14x=910
б) 2002x=13010
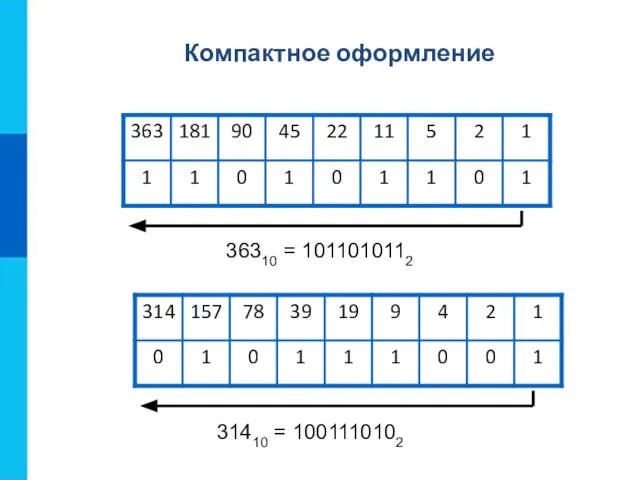
Переведите целые числа из десятичной системы счисления в двоичную:
а) 89
б) 600
в) 2010
Переведите целые числа из десятичной системы счисления в восьмеричную:
а) 513
б) 600
в) 2010
Переведите целые числа из десятичной системы счисления в шестнадцатеричную:
а) 513
б) 600
в) 2010
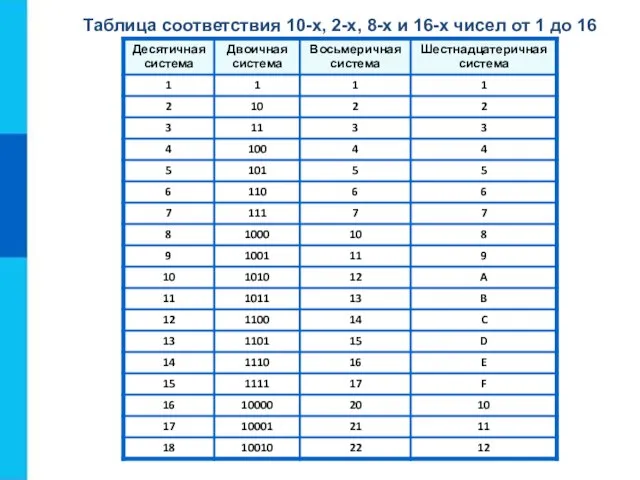
Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основаниями 2, 8, 10 и 16.
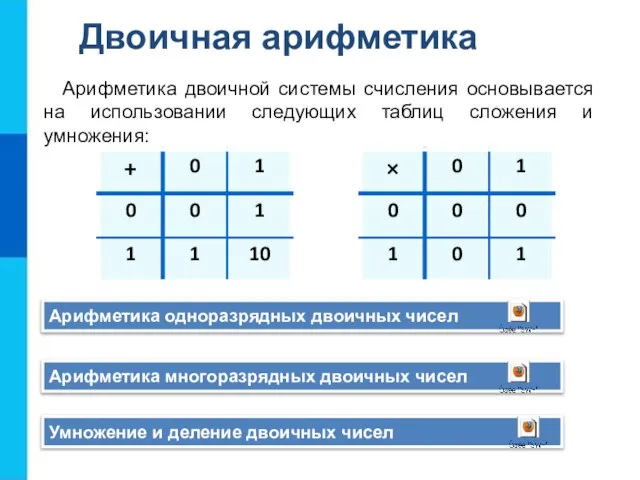
Выполните операцию сложения над двоичными числами:
а) 101010 + 1101
б) 1010 + 1010
в) 10101 + 111
Выполните операцию умножения над двоичными числами:
а) 1010 · 11
б) 111 · 101
в) 1010 · 111
Расставьте знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе:
а) 1100 ? 11 ? 100 = 100000;
б) 1100 ? 10 ? 10 = 100;
в) 1100 ? 11 ? 100 = 0.
Вычислите выражения:
а) (11111012 +AF16):368
б) 1258 + 1012 ·2A16 – 1418
Ответ дайте в десятичной системе счисления.
Задачник «Системы счисления»

Опорный конспект
Непозиционная
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
Aq =±(an–1× qn–1 + an–2 × qn–2 +…+ a0 × q0 + a–1 × q–1 +…+ a–m × q–m).
Система счисления — это знаковая система, в которой приняты определённые правила записи чисел.
Цифры - знаки, при помощи которых записываются числа.
Алфавит - совокупность цифр системы счисления.
Система счисления
Двоичная
Десятичная
Восьмеричная
Шестнадцатеричная
Римская
Позиционная