Слайд 2Понятие
Алгоритм – это формально описанная вычислительная процедура, получающая исходные данные и выдающая

результат вычисления на выход.
Слайд 3Понятие через отображение
Алгоритм – это некая функция или отображение, которая определяется как

F: X->Y
X – множество исходных данных
Y – множество значений
Слайд 4Виды алгоритмов
Механический или жесткий
Вероятностный
Эвристический
Линейный
Ветвящийся
Циклический
Вспомогательный

Слайд 5Свойства алгоритма
Детерминированность
Понятность
Результативность
Дискретность
Массовость
Конструктивность объектов

Слайд 6Детерминированность
Предписание, задающее алгоритм должно выполняться однозначно и последовательно для получения конкретного и

однозначного результата
Слайд 7Понятность
Все действия должны быть однозначно поняты и выполнены исполнителем, т.е. должны принадлежать

системе действий данного исполнителя
Слайд 8Результативность
Указывает на наличие таких исходных данных, для которых реализуемый по заданному алгоритму

вычислительный процесс должен через конечное число шагов остановиться и выдать искомый результат
Слайд 9Дискретность
Алгоритм представляет собой упорядоченное конечное множество шагов для получения результата, то есть

в любом алгоритме для каждого шага (кроме последнего), можно указать следующий за ним шаг.
Слайд 10Массовость
Каждый алгоритм предназначен для решения любой задачи из некоторого бесконечного множества однотипных

задач
Слайд 11Конструктивность объектов
Исходные объекты, промежуточные и конечные результаты – это конструктивные объекты, которые

могут быть построены целиком или допускают кодирование в каких-то алфавитах
Слайд 12Эффективность алгоритма
Скорость сходимости
Время выполнения
Удобство использования
Простота
Читаемость

Слайд 13Способы описания алгоритма
Словестное описание
Математическая запись
Графическая запись
Запись на псевдокоде
Запись на ЯП

Слайд 14Правильный алгоритм
Алгоритм считается правильным, если при любом допустимом входе он заканчивает работу

и выдает результат, удовлетворяющий требованиям задачи.
Алгоритм называется однозначным, если для одних и тех же данных он дает один и тот же ответ
Слайд 15Неправильный алгоритм
Не завершает работу
Дает неверный результат

Слайд 16Типы ошибок в алгоритме
Синтаксические
(a+b*(a+c)
Семантические
S*N, S – строка, N - число
Логические
Расстояние =

скорость + время
Слайд 17Этапы разработки программы
Анализ постановки задач
Построение математической модели
Разработка алгоритма
Анализ алгоритма
Док-во правильности алгоритма
Реализация алгоритма
Тестирование

программы
Оформление документации
Слайд 18Анализ постановки задач
Выяснить при этом входную и выходную информацию, определить идею решения,

полноту входной информации, сформулировать, накладываемые на входную информацию ограничения (то есть описать спецификации)
Слайд 19Построение математической модели
Определить какие математические структуры больше подходят для задачи, существуют ли

аналоги решения этой задачи. После чего проверить полноту математической модели, удобство работы с ней, реализации
Слайд 20Разработка алгоритма
На этом этапе необходимо тщательно обдумать алгоритм, уяснить его достоинства и

недостатки, постараться избавиться от последних и усилить первые
Слайд 21Анализ алгоритма
Оценить какой это алгоритм(линейный, с ветвлениями, с циклами). Т.е. оценить его

сложность по памяти и/или быстродействию.
Слайд 22Док-во правильности алгоритма
Предусматривает как доказательство конечности алгоритма, так и анализ его работы

на всех ветвях на разных типах входных данных
Слайд 23Реализация алгоритма
Это означает необходимость написания программы на некотором языке программирования и отладка

его на реальном компьютере
Слайд 24Тестирование программы
Т.е. провести ее как теоретическое, так и экспериментальное тестирование. Для алгоритма

необходимо подготовить полный набор тестов (минимальное подмножество входных данных, покрывающее все случаи)
Слайд 25Оформление документации
Описать технические характеристики, структуру входных и выходных данных, правила использования программы,

при необходимости – реализуемые алгоритмы и возможности модификации.
Слайд 26Размерность задачи
Размерностью задачи (l) будем называть количество информации достаточного для описания задачи

Слайд 27Сложность алгоритма
Временная сложность - T(l)
время работы алгоритма
Емкостная сложность – S(l)
объем памяти для

реализации алгоритма
Слайд 28Пример
for( i=0; i < n; i++)
for( j = n-1; j >

i; j-- )
if ( a[j-1] > a[j] )
swap(a[j-1], a[j]);
l = n+1
T(l) = cn2
S(l) = n+3
Слайд 29Мера сложности алгоритма
Сложность в худшем случае
Усредненная сложность

Слайд 30Сложность в худшем случае
Зная время работы в худшем случае, мы можем гарантировать,

что выполнение алгоритма закончится за некоторое время, даже не зная, какой именно вход (данного размера) попадется.
На практике «плохие» входы (для которых время работы близко к максимуму) могут часто попадаться. Например, для базы данных плохим запросом может быть поиск отсутствующего элемента (довольно частая ситуация).
Время работы в среднем может быть довольно близко к времени работы в худшем случае. Пусть, например, мы сортируем случайно расположенные n чисел в помощью процедуры Сортировка вставками.
Слайд 31Асимптотические обозначения
Анализируя алгоритм, можно стараться найти точное число выполняемых им действий. Но

в большинстве случаев достаточно оценить асимптотику роста времени работы алгоритма при стремлении размера входа к бесконечности (asymptotic efficiency)
Слайд 33f(n) = о(g(n))
2n = o(n2)
log2n = o(n)
n2/2 ≠ o(n2)
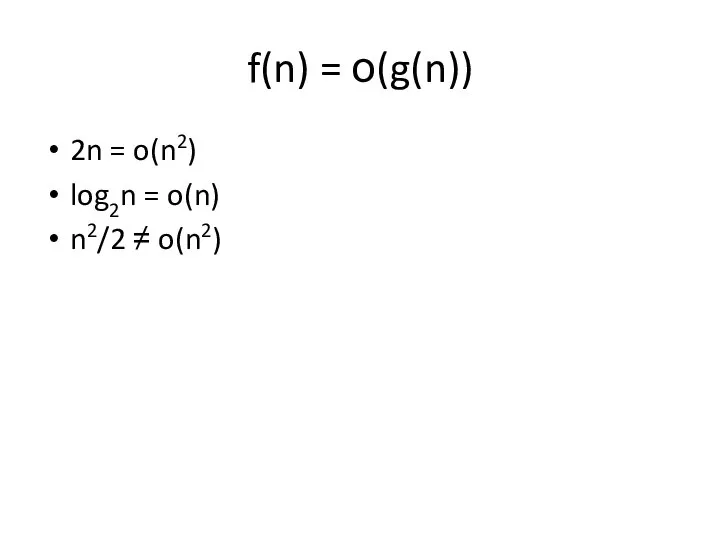
Слайд 35f(n) = ω(g(n))
2n2 = ω(n)
n = ω(ln n)
n2/2 ≠ ω(n2)
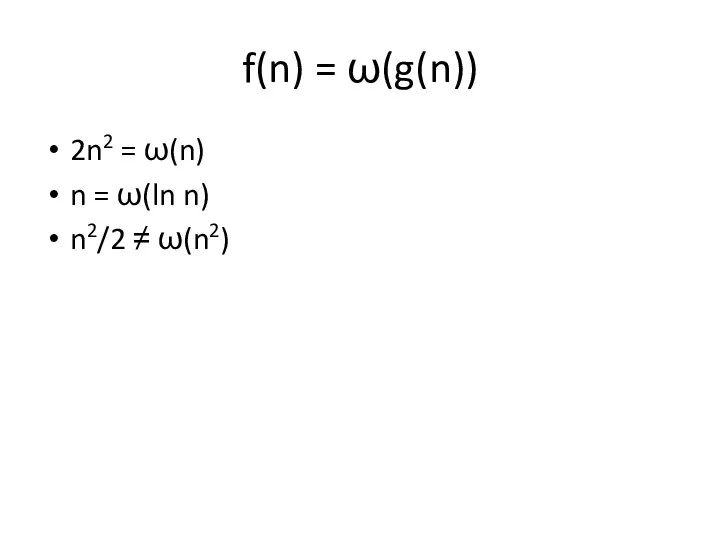
Слайд 37f(n) = Θ(g(n))
n2/2 = Θ(n2)
n2-n+2 = Θ(n2)
Если f(n) = Θ(g(n)) и h(n)

= Θ(g(n)), это не значит, что f(n) = h(n)
Слайд 38f(n) = Θ(g(n))
Отыскивая асимптотически точную оценку для суммы, мы можем отбрасывать члены

меньшего порядка, которые при больших n становятся малыми по сравнению с основным слагаемым.
Заметим также, что коэффициент при старшем члене роли не играет
Слайд 39f(n) = O(g(n))
f(n) = O(g(n)), если найдется c>0 и n0, что

при всех n≥ n0 выполнено
0≤f(n)≤сg(n)
Говорят, что g(n) есть верхняя оценка f(n).
Слайд 40f(n) = Ω(g(n))
f(n) = Ω(g(n)), если найдется c>0 и n0, что при

всех n≥ n0 выполнено
0≤cg(n)≤f(n)
Говорят, что g(n) есть нижняя оценка f(n).
Слайд 41Теорема
f(n) = Θ(g(n))
равносильно условию
f(n) = O(g(n)) и f(n) = Ω(g(n))

Слайд 42Транзитивность
f(n) = о(g(n)) и g(n) = о(h(n)) => f(n) = о(h(n))
f(n) =

ω(g(n)) и g(n) = ω(h(n)) => f(n) = ω(h(n))
f(n) = Θ(g(n)) и g(n) = Θ(h(n)) => f(n) = Θ(h(n))
f(n) = O(g(n)) и g(n) = O(h(n)) => f(n) = O(h(n))
f(n) = Ω(g(n)) и g(n) = Ω(h(n)) => f(n) = Ω(h(n))
Слайд 43Рефлекcивность
f(n) = Θ(f(n))
f(n) = O(f(n))
f(n) = Ω(f(n))

Слайд 44Симметричность
f(n) = Θ(g(n)) ⬄ g(n) = Θ(f(n))
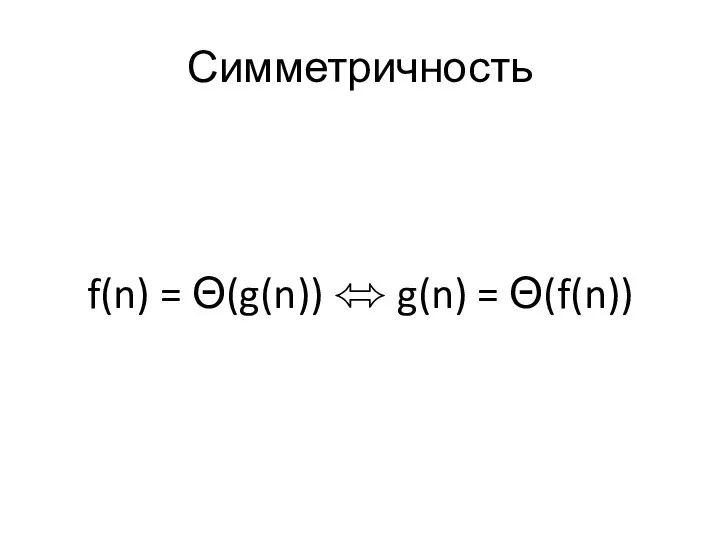
Слайд 45Обращение
f(n) = O(g(n)) ⬄ g(n) = Ω(f(n))
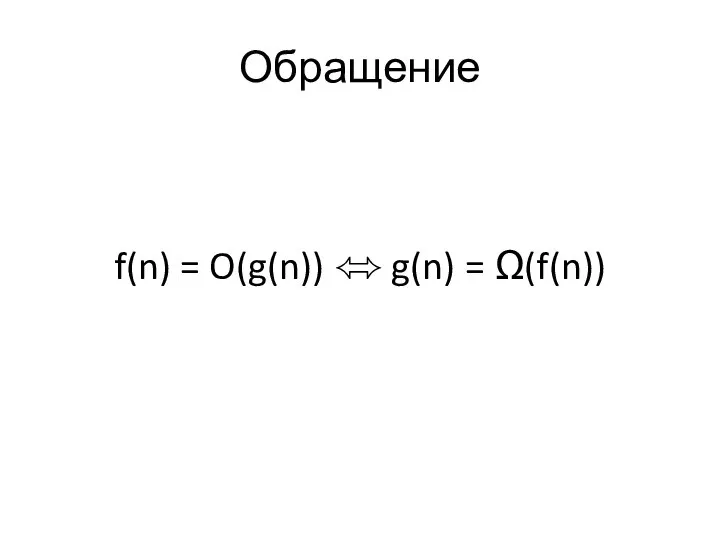
Слайд 46Эффективность алгоритмов
Полиномиальные – f(n) = O(nm)
Экспоненциальные - f(n) = O(ap(n))
Факториальные f(n) =

O(n!)
Слайд 47Полиномиальные алгоритмы
Постоянный - f(n) = O(1)
Линейный - f(n) = O(n)
Квадратный - f(n)

= O(n2)
Кубический - f(n) = O(n3)
Слайд 48Примеры полиномиальных алгоритмов
К линейным алгоритмам относится алгоритм нахождения суммы десятичных чисел, состоящих

из n1 и n2 цифр. Сложность алгоритма - O(n1 + n2).
Более общий класс полиномиальных алгоритмов –
алгоритмы деления,
извлечения квадратного корня,
решение систем линейных уравнений и др
Слайд 49Примеры экспоненциальных алгоритмов
Задачи, в которых требуется построить:
множество всех подмножеств данного множества,

все полные подграфы некоторого графа все поддеревья некоторого графа.
Слайд 50Другие типы задач
Кратчайшее решение «пятнашек» размера nxn
Задача коммивояжёра
Проблема раскраски графа
Сапер (игра)
Тетрис
составление расписаний,

учитывающих определенные условия;
размещение обслуживающих центров (телефон, телевидение, срочные службы) для максимального числа клиентов при минимальном числе центров;
оптимальная загрузка емкости (рюкзак, поезд, корабль, самолёт) при наименьшей стоимости;
оптимальный раскрой (бумага, картон, стальной прокат, отливки), оптимизация маршрутов в воздушном пространстве, инвестиций, станочного парка;
задача распознавания простого числа
Слайд 51Числа Фибоначчи
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55….
F0=0, F1=1,

Fn=Fn-1+Fn-2, n>1
Рекурсивный алгоритм
Нерекурсивный алгоритм
Слайд 52Рекурсивный алгоритм
int Fibonacci(int n){
if(n==0)
return 0;
if(n==1)
return 1;
return Fibonacci(n-1)+Fibonacci(n-2);
}

Слайд 53Нерекурсивный алгоритм
int Fibonacci(int n){
if(n==0)
return 0;
int prev = 0;
int current = 1;
for(int i=2;i<=n;++i)
{
int

temp = current;
current += prev;
prev = temp;
}
return current;
}































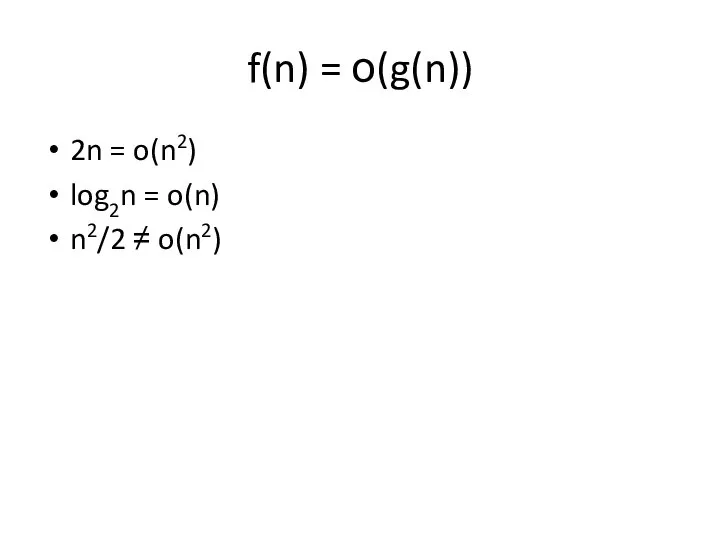

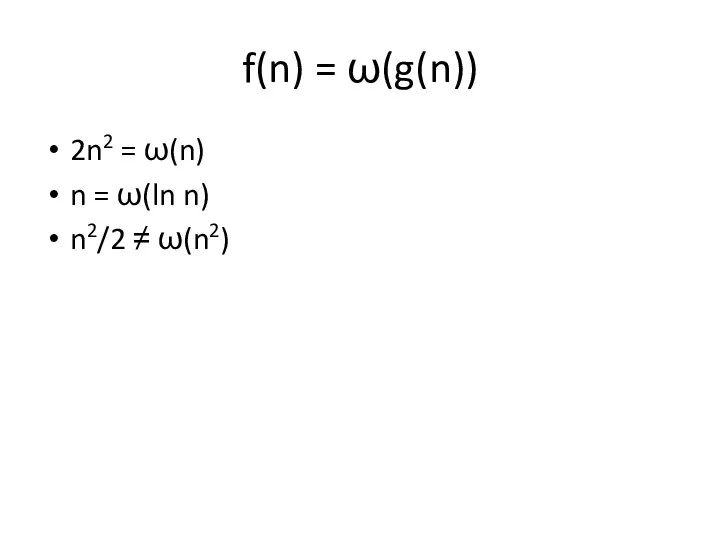








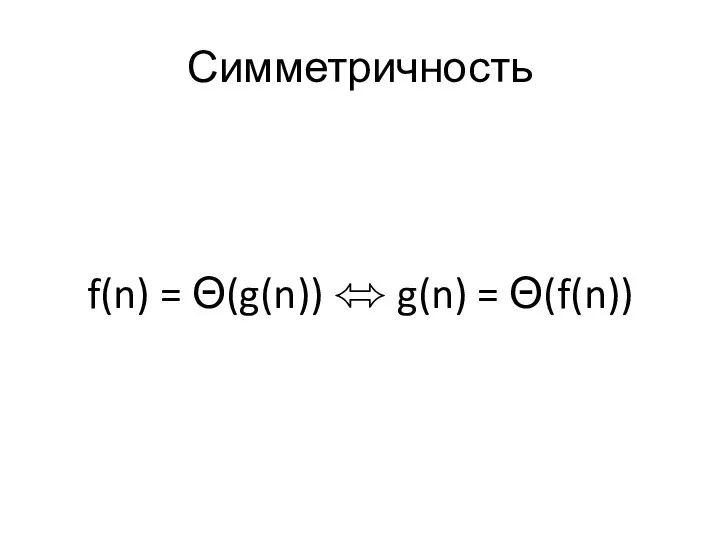
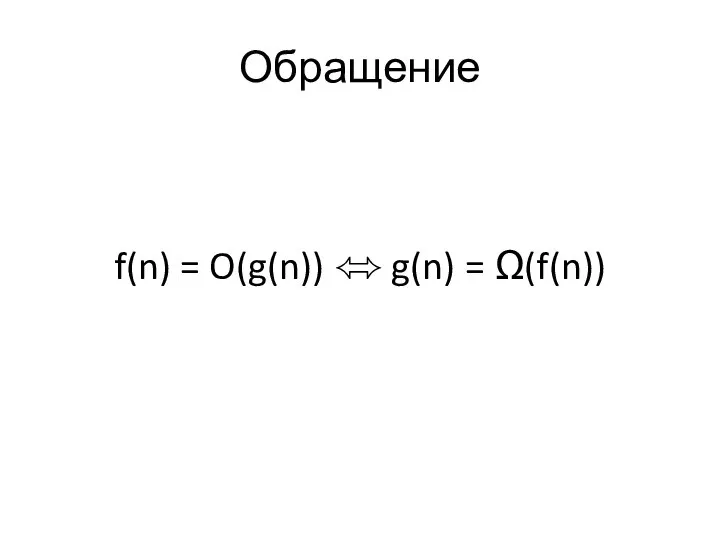








 Факториальная система счисления
Факториальная система счисления Data Warehouse Concepts and Architectures
Data Warehouse Concepts and Architectures Добро пожаловать в Мобильную Электронную Школу!
Добро пожаловать в Мобильную Электронную Школу! Механизм оффлайновых взаиморасчетов с партнерами
Механизм оффлайновых взаиморасчетов с партнерами Формула. Набор символов, написанный по специальным правилам и используемый для расчетов
Формула. Набор символов, написанный по специальным правилам и используемый для расчетов Личный кабинет ГИС ЖКХ
Личный кабинет ГИС ЖКХ Введение в логику
Введение в логику Введение в HTML. Основы WEB-технологий
Введение в HTML. Основы WEB-технологий Получение сведений из фонда данных государственной кадастровой оценки
Получение сведений из фонда данных государственной кадастровой оценки Его Величество Интернет
Его Величество Интернет 9-1-2
9-1-2 Сайт yarmetro.ru
Сайт yarmetro.ru Банк ВТБ. Предложения по оптимизации резервирования независимых каналов связи. Терминология сетей Ростелеком
Банк ВТБ. Предложения по оптимизации резервирования независимых каналов связи. Терминология сетей Ростелеком Описательные статистики
Описательные статистики Работа в интернет пространстве и с социальными сетями
Работа в интернет пространстве и с социальными сетями Заполнение платежных документов по графикам оплаты
Заполнение платежных документов по графикам оплаты Информационные системы управления
Информационные системы управления Аватария - мир, где сбываются мечты
Аватария - мир, где сбываются мечты Онлайн-форум. Пользователи Paramount+
Онлайн-форум. Пользователи Paramount+ Единицы измерения информации
Единицы измерения информации Автоматизация деятельности турагентства
Автоматизация деятельности турагентства Обработка информации с помощью электронных таблиц. Практическое занятие. Часть II
Обработка информации с помощью электронных таблиц. Практическое занятие. Часть II Муравьиные сказки. Часть 2
Муравьиные сказки. Часть 2 Типы алгоритмов
Типы алгоритмов Программирование. Введение (
Программирование. Введение ( Prezentatsia_Microsoft_PowerPoint_1
Prezentatsia_Microsoft_PowerPoint_1 CSS Position
CSS Position Компьютерные сети. Линейная топология
Компьютерные сети. Линейная топология