Содержание
- 2. Сложение одноразрядных двоичных чисел: 0 + 0 = 0 1 + 0 = 1 0 +
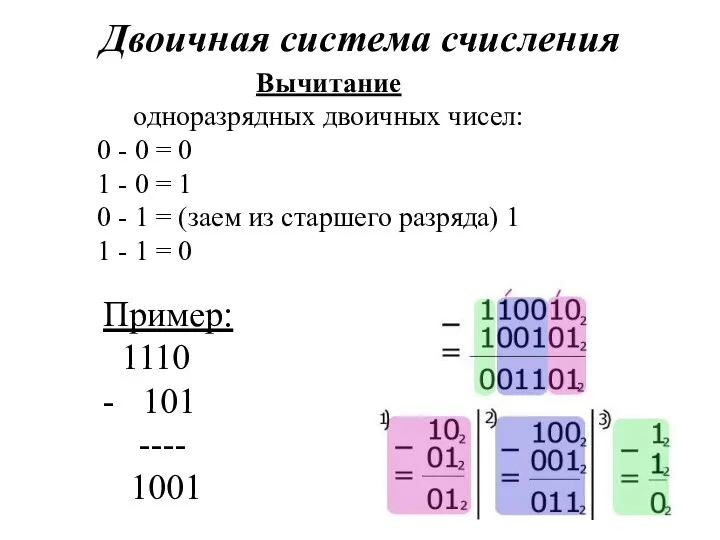
- 3. Вычитание одноразрядных двоичных чисел: 0 - 0 = 0 1 - 0 = 1 0 -
- 4. Двоичная система счисления Умножение одноразрядных двоичных чисел: 0 * 0 = 0 1 * 0 =
- 5. Двоичная система счисления Деление выполняется так же как в десятичной системе счисления:
- 6. Выполнение арифметических операций над двоичными числами разных порядков: сравниваются и выравниваются порядки; выполняется сложение или вычитание
- 7. Выполнение арифметических операций над двоичными числами разных порядков: Пример. Сложение Х1=0,1001*2101 Х2=0,1100*2100 1) Δр=101-100=001 Х2=0,0110*2101 2)0,1001
- 8. Выполнение арифметических операций над двоичными числами разных порядков: Пример. Вычитание Х1=0,1001*2101 Х2=0,1100*2100 1) Δр=101-100=001 Х2=0,0110*2101 2)
- 9. Выполнение арифметических операций над двоичными числами разных порядков: Пример. Умножение Х1=q1*2p1 Х2=q2*2p2 X1*X2=q1*q2*2(p1+p2) Х1=10=0,10*210 Х2=10=0,10*210 0,10
- 10. Выполнение арифметических операций над двоичными числами разных порядков: Пример. Деление Х1=q1*2p1 Х2=q2*2p2 Х1=0,110=110*2-11 Х2=0,10=10*2-10 р1-р2=-11-(-10)=-01 =11*2-01
- 11. В ПК используются следующие разрядные сетки для представления чисел: 1 байт (8 разрядов) – полуслово 2
- 12. Выполнение арифметических операций в машинных кодах позволяет: свести операцию вычитания к операции сложения автоматически получать знак
- 13. Виды машинных кодов Прямой код числа представляется в виде абсолютной величины со знаком двоичного числа –
- 14. Виды машинных кодов Обратный код отрицательного числа получается с помощью замены значений всех цифр числа на
- 15. Виды машинных кодов Дополнительный код отрицательного числа получается в результате увеличения его обратного кода на 1.
- 16. Все математические операции в ПК выполняются только в обратных или дополнительных кодах.
- 17. Пример 1. Выполнение операции в обратном коде Х1-Х2=17-5= 17+(-5)=12 [Х1] пр=00010001 [Х1] обр=00010001 [Х2] пр=10000101 [Х2]
- 18. Пример 2. Х1-Х2=5-17= 5+(-17)=-12 [Х1] пр=00000101 [Х1] обр=00000101 [Х2] пр=10010001 [Х2] обр=11101110 00000101 +11101110 11110011 обр.
- 19. Пример 3. Выполнение операции в дополнительном коде Х1-Х2=17-5= 17+(-5)=12 [Х1] пр=00010001 [Х1] обр=00010001 [Х1] доп=00010001 [Х2]
- 20. Пример 4. Х1-Х2=5-17= 5+(-17)=-12 [Х1] пр=00000101 [Х1] обр=00000101 [Х1] доп=00000101 [Х2] пр=10010001 [Х2] обр= 11101110 [Х2]
- 21. Модифицированный дополнительный машинный коды Модифицированный дополнительный код получается из дополнительного простым дублированием знакового разряда. "00" соответствует
- 22. Пример Переведем X и Y в модифицированный дополнительный код: Выполним сложение: В данном примере запятой отделены
- 24. Скачать презентацию














![Пример 1. Выполнение операции в обратном коде Х1-Х2=17-5= 17+(-5)=12 [Х1] пр=00010001 [Х1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1034096/slide-16.jpg)
![Пример 2. Х1-Х2=5-17= 5+(-17)=-12 [Х1] пр=00000101 [Х1] обр=00000101 [Х2] пр=10010001 [Х2] обр=11101110](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1034096/slide-17.jpg)
![Пример 3. Выполнение операции в дополнительном коде Х1-Х2=17-5= 17+(-5)=12 [Х1] пр=00010001 [Х1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1034096/slide-18.jpg)
![Пример 4. Х1-Х2=5-17= 5+(-17)=-12 [Х1] пр=00000101 [Х1] обр=00000101 [Х1] доп=00000101 [Х2] пр=10010001](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1034096/slide-19.jpg)


 База данных Access
База данных Access Дизайн и Верстка Системы Организации Видео Архива (СОВА)
Дизайн и Верстка Системы Организации Видео Архива (СОВА) Принципы ООП
Принципы ООП Электронные больничные. СБИС+
Электронные больничные. СБИС+ Основные теоретические вопросы проектирования ПОР. Увеличение частоты дискретизации (Интерполяция) цифрового сигнала
Основные теоретические вопросы проектирования ПОР. Увеличение частоты дискретизации (Интерполяция) цифрового сигнала 1С Управление производственным Предприятием 1.3. ООО Завод Невский Ламинат
1С Управление производственным Предприятием 1.3. ООО Завод Невский Ламинат Трихадеры в rainbow six
Трихадеры в rainbow six Понятие информация
Понятие информация Понятие массива. Одномерные и двумерные массивы
Понятие массива. Одномерные и двумерные массивы Эллиптическое шифрование
Эллиптическое шифрование Символьные данные
Символьные данные Форматирование текста на Web-странице
Форматирование текста на Web-странице Модель аппаратного обеспечения современных ПЭВМ с точки зрения ОС. Лекция 12
Модель аппаратного обеспечения современных ПЭВМ с точки зрения ОС. Лекция 12 Презентация на тему Основные положения Visual Basic
Презентация на тему Основные положения Visual Basic  Продвижение в Ютуб
Продвижение в Ютуб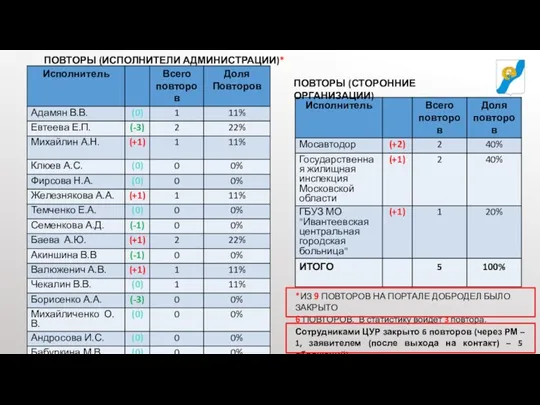 Динамика повторов
Динамика повторов Клуб успешных людей On the list
Клуб успешных людей On the list Использование веб-сервисов
Использование веб-сервисов Платформа Aliexpress
Платформа Aliexpress Операционные системы и оболочки
Операционные системы и оболочки Линейные списки
Линейные списки Одномерные массивы. Циклические сдвиги, сжатие
Одномерные массивы. Циклические сдвиги, сжатие Пятое занятие. Функции
Пятое занятие. Функции Программирование и трейдинг
Программирование и трейдинг Госуслуги. Быстро. Просто. Надежно
Госуслуги. Быстро. Просто. Надежно Компьютерные вирусы
Компьютерные вирусы PHP - Вводная лекция (2022)
PHP - Вводная лекция (2022) 2022-10-16 LandingPage для 105.ooo(4)
2022-10-16 LandingPage для 105.ooo(4)