Содержание
- 2. Словарные операции поиск элемента с заданным ключом х добавление нового элемента с заданным ключом х удаление
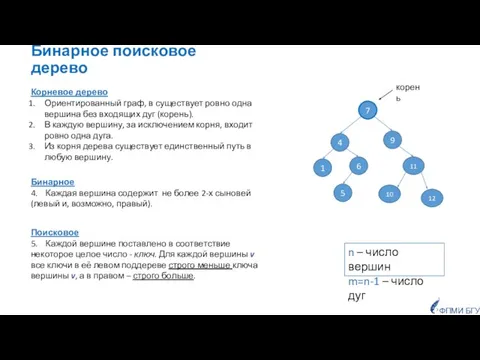
- 3. Бинарное поисковое дерево Поисковое 5. Каждой вершине поставлено в соответствие некоторое целое число - ключ. Для
- 4. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
- 5. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
- 6. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
- 7. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
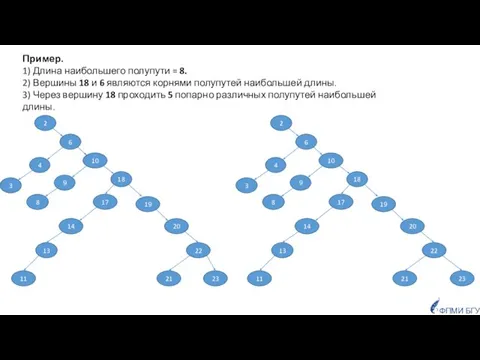
- 8. 10 18 23 21 22 20 19 11 13 14 17 6 8 9 2 Наибольшим
- 9. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
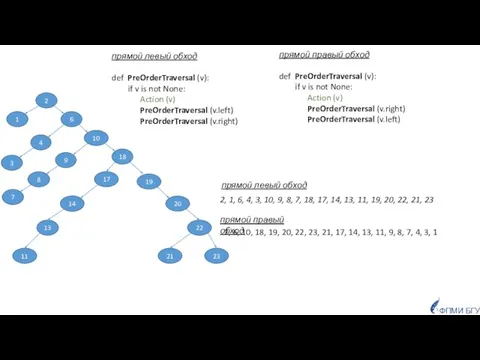
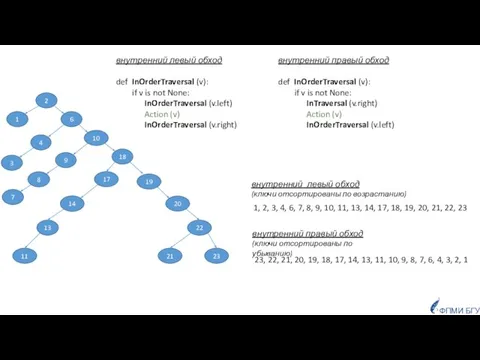
- 10. прямой (левый, правый) - PreOrderTraversal (v) ФПМИ БГУ Обходы обратный (левый, правый) - PostOrderTraversal (v) внутренний
- 11. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
- 12. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
- 13. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
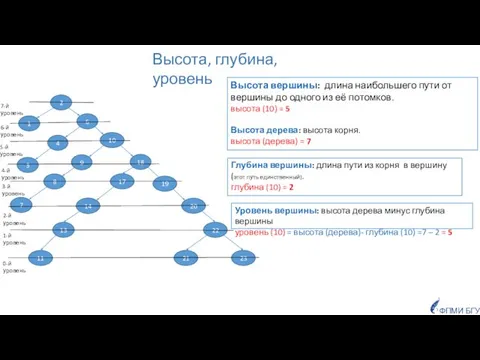
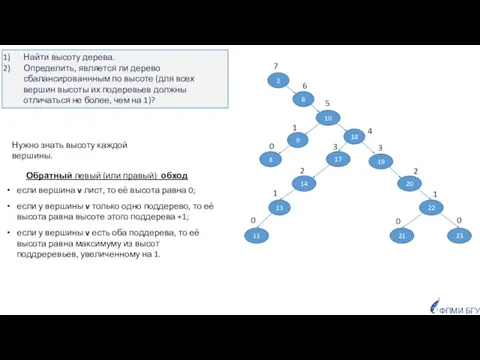
- 14. ФПМИ БГУ Примеры задач Найти высоту дерева. Определить, является ли дерево сбалансированнным по высоте? Найти длину
- 15. Обратный левый (или правый) обход если вершина v лист, то её высота равна 0; если у
- 16. 10 18 23 21 22 20 19 11 13 14 17 6 8 9 2 0
- 17. 10 18 23 21 22 20 19 11 13 14 17 6 8 9 2 0
- 18. если вершина v лист, то её метка равна 1; если у вершины v только одно поддерево,
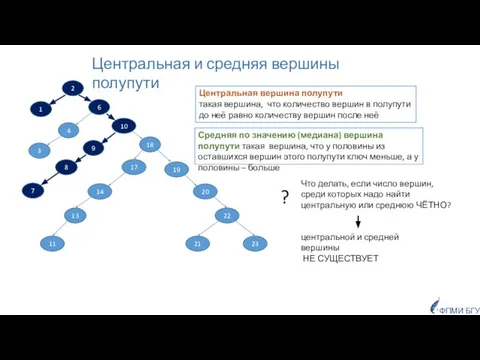
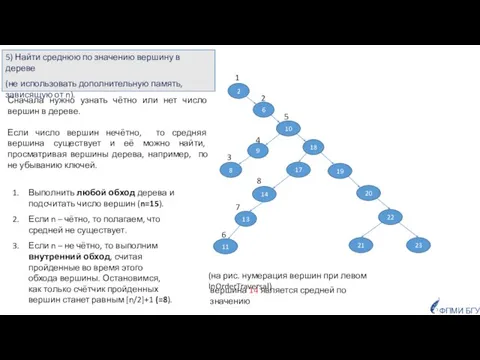
- 19. Выполнить любой обход дерева и подсчитать число вершин (n=15). Если n – чётно, то полагаем, что
- 20. Сначала обратным обходом расставить вершинам метки высот. Во время этого же обхода подсчитать количество вершин, у
- 21. m i a t u s b p f вершина t является средней по значению f
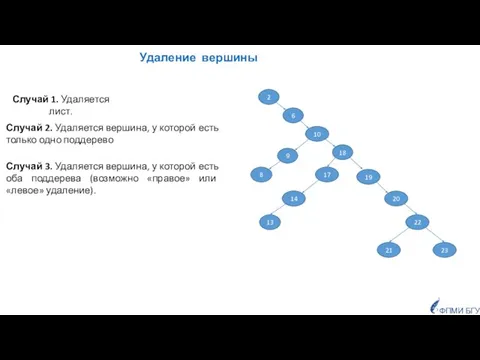
- 22. Удаление вершины ФПМИ БГУ Случай 1. Удаляется лист. Случай 2. Удаляется вершина, у которой есть только
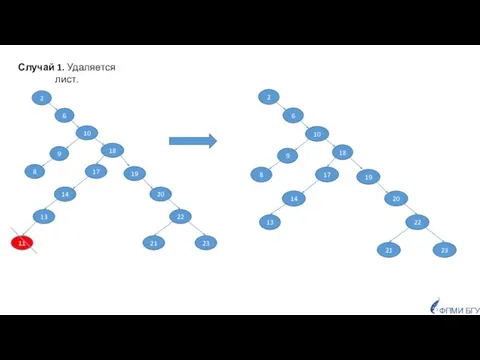
- 23. ФПМИ БГУ Случай 1. Удаляется лист.
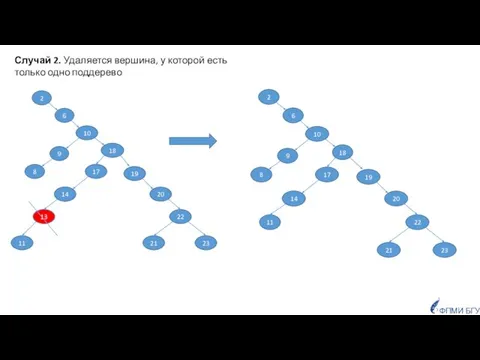
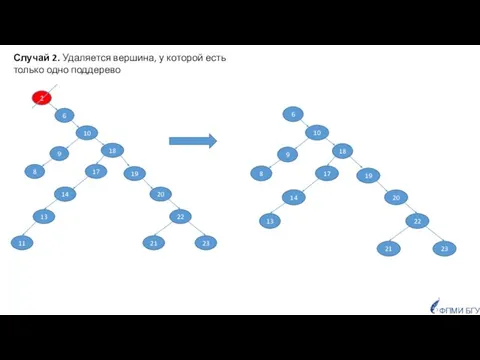
- 24. ФПМИ БГУ Случай 2. Удаляется вершина, у которой есть только одно поддерево
- 25. ФПМИ БГУ Случай 2. Удаляется вершина, у которой есть только одно поддерево
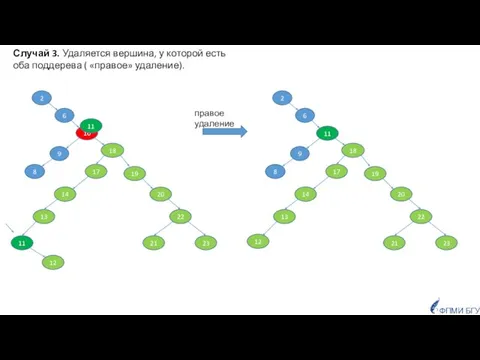
- 26. 10 18 23 21 22 20 19 11 13 14 17 6 8 9 2 правое
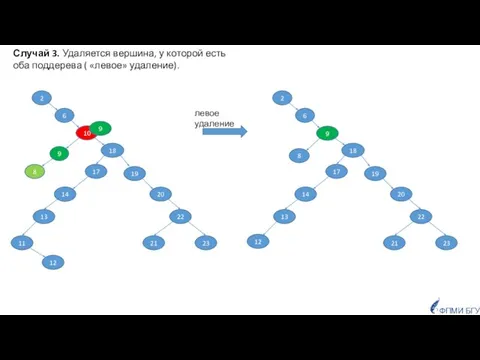
- 27. 10 18 23 21 22 20 19 11 13 14 17 6 8 9 2 левое
- 28. !!! Если у удаляемой вершины только одно поддерево, то НЕТ ПОНЯТИЯ ПРАВОЕ/ЛЕВОЕ удаление. Удаление всегда выполняется
- 29. Оценки числа операций в худшем случае 10 18 19 6 2 построение дерева для последовательности из
- 30. ФПМИ БГУ В 1962 году советские учёные Г.М.Адельсон-Вельский и Е.М.Ландис предложили структуру данных сбалансированного поискового дерева.
- 31. Георгий Максимович Адельсон-Вельский Евгений Михайлович Ландис
- 32. ФПМИ БГУ В рамках дисциплины в дальнейшем мы подробно исследуем эту структуру данных, а пока лишь
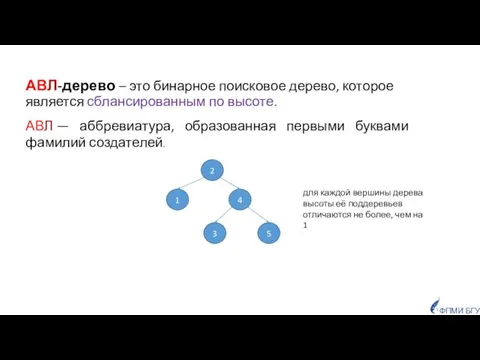
- 33. АВЛ-дерево – это бинарное поисковое дерево, которое является сблансированным по высоте. 2 4 1 3 5
- 34. ТЕОРЕМА. Пусть n – число внутренних вершин АВЛ-дерева, а h – его высота. Тогда справедливы следующие
- 35. Использование поисковых деревьев на практике ФПМИ БГУ
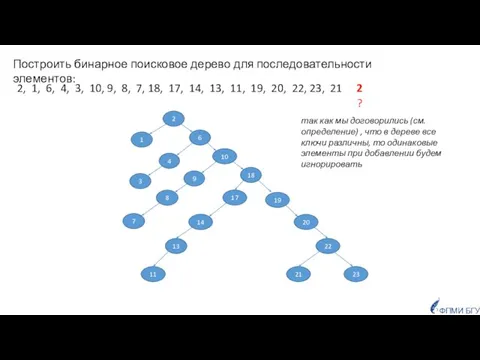
- 36. Сортировка деревом Предположим, что на вход поступаю числа, среди которых нет повторяющихся. Рассмотрим следующий алгоритм сортировки.
- 37. Абстрактный тип данных: множество (set) Множество (англ. set) —хранит набор попарно различных объектов без определённого порядка.
- 38. Абстрактный тип данных ассоциативный массив (map) Ассоциативный массив (англ. associative array), или отображение (англ. map), или
- 39. Сборник задач по теории алгоритмов : учеб.-метод. пособие / В.М. Котов, Ю.Л. Орлович, Е.П. Соболевская, С.А.
- 41. Скачать презентацию





















 Tagul - web-сервис
Tagul - web-сервис Упаковка контента (нейминг)
Упаковка контента (нейминг) Справка по заполнению формы Перечень обособленных подразделений ЛПУ (без ФАП и ФП), требующих подключения к сети Интернет
Справка по заполнению формы Перечень обособленных подразделений ЛПУ (без ФАП и ФП), требующих подключения к сети Интернет Дизассемблирование циклов. Реверс-инжиниринг
Дизассемблирование циклов. Реверс-инжиниринг Растровая и векторная графика. Информатика для СПО
Растровая и векторная графика. Информатика для СПО Операторы. Операторы управления
Операторы. Операторы управления Методика SMART
Методика SMART Кодирование информации
Кодирование информации Применение электронной системы Hawk-Eye в различных видах спорта
Применение электронной системы Hawk-Eye в различных видах спорта Лабораторные работы по дисциплине: Базовые информационно-коммуникационные технологии
Лабораторные работы по дисциплине: Базовые информационно-коммуникационные технологии Сын Потапа. Рresentation csgo operation
Сын Потапа. Рresentation csgo operation Модернизация клиентской части ЕМГИС Объекты потребительского рынка и земельные участки
Модернизация клиентской части ЕМГИС Объекты потребительского рынка и земельные участки Кодирование и шифрование данных
Кодирование и шифрование данных Создание 3D модели на основе операций твердотельного моделирования.(2 занятие)
Создание 3D модели на основе операций твердотельного моделирования.(2 занятие) Социальные группы
Социальные группы Table of Contents
Table of Contents Принципы построения телекоммуникационных вычислительных сетей (ТВС)
Принципы построения телекоммуникационных вычислительных сетей (ТВС) Zoom. Конференция для участника
Zoom. Конференция для участника Республиканский конкурс ИТ-Чемпион
Республиканский конкурс ИТ-Чемпион Алгоритмическая система Кумир
Алгоритмическая система Кумир Выберите файл
Выберите файл Кроссворд
Кроссворд Безопасный интернет
Безопасный интернет Сайт знакомств BezDebilov
Сайт знакомств BezDebilov Глава 2. Компьютер как универсальное устройство для работы с информацией. Тема 2.1. Основные компоненты компьютера и их функции
Глава 2. Компьютер как универсальное устройство для работы с информацией. Тема 2.1. Основные компоненты компьютера и их функции Аппаратное обеспечение ПК
Аппаратное обеспечение ПК Искусственные и естественные источники информации
Искусственные и естественные источники информации ORM в 1С-Битрикс. Выборка данных
ORM в 1С-Битрикс. Выборка данных